Дифракционный расчет фокусаторов в фокальные кривые в рамках электромагнитной теории

Рассмотрен расчет дифракционных оптических элементов для формирования фокальных кривых в рамках асимптотического подхода. В криволинейных координатах получено простое выражение для функции эйконала. Приведены расчеты поля от фокусаторов в кольцо и отрезок.

1. Постановка задачи фокусировки в фокальные кривые

Данная работа посвящена решению обратных задач дифракционной оптики. Ограничимся рассмотрением пропускающих дифракционных оптических элементов, освещаемых плоской электромагнитной волной. Рассмотрим общий случай постановки обратных задач дифракции в рамках электромагнитной теории.

Пусть монохроматическая электромагнитная волна, описываемая четырехкомпонентным бивектором W ( x ’, x ^-, x ³) - падает на дифракционный оптический элемент (ДОЭ) [1]. Для описания энергетических характеристик электромагнитного поля в области регистратора [1] вводятся две физических величины.

I w| = — Eee* + Hн О(1)

8п''

- объемная плотность энергии,

S = — Re ГE х H* 1

8п

- вектор Умова-Пойтинга, где с - скорость света в вакууме,

E -напряженность электрического поля, H - напряженность магнитного поля.

Для вектора Умова-Пойтинга справедлива теорема c div Re ГE(ю), H*(ю)] =

=--- E ? ( ю ) E i * ( ю )( е * ( ю ) -е ( ю )) -

16 п

——

- — н ( ю ) н ( ю )( ц ( ю ) -ц ( ю )) - 16 п

* *                                         **

- Re I - jeE ( ю ) I- Re I - j mH ( ю )

Для непоглощающей среды выражение приоб- ретает вид: div Re I = 0, где I = — ГE, H* 1 - ком-8nLJ плексный вектор Пойнтинга.

В интегральной форме: f I dS = 0.

S

В случае, когда регистратор представляет собой плоскость, перпендикулярную оси x ³ , удобно ввести скалярную величину, равную проекции вектора Умова-Пойтинга на нормаль к плоскости регистратора.

Введем в пространстве четырехкомпонентных векторов функций W понятие скалярного произведения. Введем скалярное произведение таким образом, чтобы оно не зависело от координаты z, и в то же время произведение вектора самого на себя было пропорционально потоку вектора Умова-Пойтинга. Для этого запишем уравнения Максвелла в обычной форме для поля E1 H1 и для комплексно сопряженного поля rot E1 = ikH1

rot H 1 = - ikE 1 rot E *- = - ik H *- rot H *- = ik E *-

вычитаем второе уравнение из первого и, используя известную формулу векторного анализа

H *- rotE 1 - E 1 rot H * - = ik H 1 H *- - ik E 1 E *2

E *2 rotH 1 - H 1 rot E *2 = - ik E 1 E *2 + ik H 1 H *2     (6)

div[a,b] = b rot a - a rotb , получаем следующее выражение div[E1,H*2 ] - div[H„K*2 ] = 0                 (7)

или div ([K„H*2 ] + [E*2,H, ]) = 0.

Далее, используя теорему Остроградского-Гаусса и учитывая условия излучения (с целью зануления интеграла по боковой поверхности), получаем

JJ ( [ E t ^{( x} , У , ^z1 ), H *2 ^{( x} , У , z l ^)] +

+ [ E *2 ( x , y , Z l ), H t ( x , y , Z l )] ) dxdy = = JJ ( ^{[ E} t ⁽ x ’ У ’ z 2 )’ ^H *2 ⁽ x ’ У ’ z 2 ^{)] +}

+ [ E *2 ( x , y , z 2 ), H t ( x , y , z 2 )] ) dxdy .

Запишем выражение (8) в следующем виде

JJ A (( x , y , z 1 )) Q B * ( x , y , z 1 ) dxdy =

= JJ A T (( x , у , z 2 )) ^ B * ( x , у , z 2 ) dxdy , где

'0   0    01

0 0 - 10

Q = 0 -100

41   0    00

или

JJ ( A ( x , У , z 2 ), B ( x , y , z 2 ) dxdy =

= JJ ( A ( x , У , z 1 ), B ( x , y , z )} dxdy ,

где

■ = (AT) QB - псевдоскалярное произве дение в пространстве четырехкомпонентных матриц-столбцов. Формула означает, что оператор распространения сохраняет скалярное произведение

< A о B >=

8 c -JJ <  A , B >  dxdy ,

т.е. является в пространстве с данным скалярным произведением унитарным оператором. Это свойство сохранения скалярного произведения можно использовать для решения обратных задач дифракции. Это в значительной мере упрощает вычисление градиента функционала невязки по аналогии с тем, как это делается в случае скалярного приближения [2]. Кроме того, наличие сохраняющейся величины можно использовать для контроля правильности решения прямой задачи дифракции.

Обратная задача фокусировки состоит в расчете параметров области модуляции по заданному распределению интенсивности или объемной плотности в области регистратора. Расчет параметров области модуляции сводится к расчету функции микрорельефа или к расчету распределения показателя преломления. Точное решение обратной задачи во многих случаях не существует, поэтому практически во всех случаях будем искать приближенное решение. Данную задачу можно решать в различных приближениях. Анализ приближений в случае решения обратной задачи дифракции совпадает с решением прямой задачи дифракции.

В данной работе при рассмотрении обратных задач дифракции на оптическом элементе будут использоваться следующие приближения

• 1.    В области 1 распространение излучения будет описываться с помощью интеграла Кирхгофа-Котлера. В некоторых задачах вместо падающей

• 2.    В области подложки и области модуляции (область 2 и 3) будет использовано приближение, основанное на асимптотических методах, рассмотренных в работе [3].

• 3.    В области 4 будет использоваться расчет поля, основанный на вычислении интеграла Кирхгофа-Котлера.

волны задается распределение источников электромагнитного поля.

В рамках асимптотической теории расчет параметров области модуляции разбивается на два этапа.

• 1.    Расчет функции Ф ( x , y );

• 2.    Расчет профиля оптического элемента внутри

зоны.

Приведенная формулировка обратных задач представляет собой наиболее общую постановку обратных задач фокусировки электромагнитного излучения, поэтому ниже рассмотрим частный случай постановки, когда геометрические лучи, выходящие с поверхности оптического элемента, сходятся на некоторой кривой, расположенной в плоскости регистратора X=f Параметрические уравнения кривой имеют вид:

x ¹ = x = X © x ² = y = Y ©

где £ натуральный параметр. Согласно геометрической теории фокусаторов [2] все лучи, приходящие в данную точку на фокальной кривой, лежат на круговом конусе. Ось конуса совпадает с касательной к фокальной кривой. Угол раствора конуса меняется от точки к точке.

Уравнение конуса световых лучей имеет вид

( ( x ¹ - X ©) X '© + ( x ² - Y ©) Y ' ( ^ ) ) =

= c ²(Q ( ( x ¹ - X O² +                    (14)

+(x2 - Y©)2 + (x3 - f )2), где c(^) - косинус угла раствора конической поверхности.

Для решения прямой и обратной задачи фокусировки в произвольную фокальную кривую удобно ввести криволинейную систему координат, связанную с лучами. Для дальнейшей работы необходимо ввести систему криволинейных координат в плоскости, непосредственно прилегающей к области модуляции. Связь между криволинейными координатами в области ДОЭ (^, п) с декартовыми (u, v) имеет вид u = X © + a © V f2 +n2X '©-П Y '©    (15)

v = Y © + a © V f² +П ² Y '© + П X '©,     (16)

где a © =

c ©

Vi- c ²©.

Координатные линии данной системы координат образованы пересечением кругового конуса и плоскости (в случае, когда плоскость регистратора и дифракционного оптического элемента параллельны, это будут гиперболы). Система координат не является ортогональной. Связь криволинейных координат ^, ni с декартовыми x, у в области фокальной кривой x = X(6) ± a (6)X'©^-nY ‘(6) (18)

у = Y © ± a © Y \^Н + П 1 X '©.         (19)

Отметим, что последние соотношения описывают связь координат не на всей плоскости, а только в окрестности фокальной кривой. Для того, чтобы ввести криволинейные координаты на всей плоскости регистратора необходимо ввести понятие линейного продолжения фокальной кривой. Линейное продолжение описывается формулами x = X (6) + X '©(64))(20)

у = Y © + Y '©(64)),(21)

где

6 4, если 6 €[0, l]

6 = 0 , если 6 < 0(23)

6 = l , если 6 > l(24)

Теперь, используя понятие линейного продолжения, мы сможем ввести локальные координаты не только в окрестности фокальной кривой, но и в окрестности граничных точек.

Для характеристики распределения электромагнитной энергии вдоль фокальной кривой введем несколько билинейных по векторам электрического и магнитного поля величин

I, (6) =< W(X(6), Y(6)) о W(X(6), Y(6)) > характери- зует распределение интенсивности на геометриче- ской кривой,

1 2© = J < W ( x '©n ), x ²( 6 , n )) о

-8

o W (( x ¹ ( 6 , n ), x ²© n )) >  d n

представляет собой линейную плотность распределения энергии вдоль фокальной кривой,

I з ( 6 ) = J F ( n ) <  W ( x ¹ ( 6 , n ), x ² ( 6 , n )) о

-8

о W((x'© n), x2© n)) > dn характеризует измеряемое воздействие, например, тепловое.

Задача состоит в отыскании параметров области модуляции по одной из известных функций I .©, I 2©, I з©.

Термин измеряемое воздействие требует разъяснения. Если электромагнитное излучение падает на поверхность материального объекта, то данная поверхность за счет поглощения электромагнитной энергии будет нагреваться (именно этот эффект используется в технических приложениях). Однако повышение температуры в данной точке будет зависеть не только от плотности потока электромагнитной энергии в данной точке, но и от значения в соседних точках. Кроме того, любой измерительный прибор устроен таким образом, что измеряет не величину интенсивности в точке, а среднее значение интенсивности в некоторой окрестности. Наиболее простая связь наблюдаемой величины с интенсивностью светового поля - линейный интегральный оператор. Вид функции F(в) зависит от физического процесса, на котором основано действие данного измерительного прибора. Постановка и решение поставленных задач существенно отличаются от методов решения задач фокусировки с помощью итерационных алгоритмов, а также методов, основанных на минимизации соответствующего функционала в банаховом пространстве, так как в этом случае необходимо вместо интегральной характеристики распределения электромагнитной энергии вдоль кривой задавать распределение энергии в ее окрестности. Следует отметить, что во многих технических задачах, связанных с фокусировкой лазерного излучения, профиль распределения интенсивности поперек фокальной кривой не является существенным входным параметром задачи.

В геометрическом приближении задача расчета фокусаторов лазерного излучения сводится к отысканию функции эйконала. Функция эйконала находится из уравнения наклонов [2]

дФ =_____________X(6(u, v)) - и_____________ д и   J (X © и, v)) - и )2 +(Y © и, v)) - v )2 + f2 , дФ =______________Y (6( и, v)) - v______________ дv   л)(X(6(и, v)) - и )2 +(Y(6(и, v)) - v)2 + f2 ,

U,v - декартовые координаты в плоскости, непосредственно прилегающей к плоскости оптического элемента;

^(и, v) - определяет соответствие между точками на фокусаторе и точками на фокальной кривой.

В криволинейной системе координат уравнение наклонов представляется в виде дФ= | a(!z .(1 + °'(6)Tf^+n2)       (30)

^д^ V 1 + a² ( 6)^V                    '

дФ J 1 + a ²( 6 )

---= i      ^n ^dn V f ² +n²

Функцию эйконала можно восстановить по известной формуле из теории потенциала

Ф ( 6 , n ) = J a^l— dt + V1 + a ² ( 6 )7 f² +n ² . (32) 0^1 + a ² ( t )

Отметим, что вид функции эйконала зависит от функции a(6), которая определяет зависимость угла раствора конуса от натурального параметра вдоль фокальной кривой. Данная функция определяет линейную плотность энергии вдоль фокальной кривой.

метим, что в этом случае

( Г'. 5 5%лп - ( %Лп ) ² ) = ⁰,

2. Асимптотический расчет светового поля вблизи фокальной кривой

Рассмотрим монохроматическую электромагнитную волну, падающую на дифракционный оптический элемент, который описывается функцией эйконала Ф( u,v ).

В рамках электромагнитной асимптотической теории [1], поле в плоскости, непосредственно прилегающей к области модуляции на дифракционном оптическом элементе, имеет вид

и метод стационарной фазы становится неприменимым. В этом случае для расчета электромагнитного поля вблизи фокальной кривой будем использовать асимптотические методы вычисления интегралов, аналогичные методам, рассмотренным в работе [4].

Для вычисления интеграла Кирхгофа-Котлера разложим функцию V , ( 5 , n , 5 , , П , ) в ряд по степеням ( 5 - 5 , ) с точностью до квадратичных членов.

n =ю

W ( x , У , z ) = £ W n ( x , У , z )exp ( ikn Ф ( x , y ) ) (33) n =-ro

В матричном виде интеграл Кирхгофа-Котлера имеет вид [1]

^ , ( 5 , n , 5 , , n , ) = ^ , ( 5 , , n , 5 , , n , ) +

+^ ( 5 , , n , 5 i , n , )( 5-5 , ) +                      (40)

+^ ( 5 , , n , 5 i , п , )^ ^5- ^ ^{5 1}^- +5 ,

W ( x ) = k- [ ^{exp (} ikr ) T ( x , r W ( x ') ds        (34)

4 п s     r

В данном пункте рассмотрим поле вблизи каустической кривой. Для записи будем использовать введенные ранее криволинейные координаты. В данном параграфе будут использованы компоненты векторов, записанные в декартовых координатах. Подставляем (34) в (33) и получаем представление поля в виде суммы интегралов, каждый из которых можно вычислить с помощью метода стационарной фазы. Использование асимптотических методов позволяет избежать громоздких вычислений.

W ( x , У , f ) =

где к 5 << п .

Разложение это справедливо, так как световое поле в окрестности фокальной кривой в точке с параметром ^ формируется световым потоком, проходящим в окрестности соответствующего слоя. Размер окрестности определяется из условия

X

L^45 i , n , 5 i , n , )

X

< —.

Для использования этого разложения достаточно, чтобы условие к 5 << п выполнялось только в этой окрестности.

%’ ( 5 i , n, 5 i , n , ) =

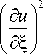
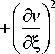
. Га ² u, +   uku (d5 ^{2 (}

\ I I д V/       \

- x + —7 V - У

) J ^д5^{2 ( Л)}

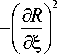
n =to

= z n=-ГО

exp ( ik Y n ( 5 ' , n n • st 5 i , П 1 ) ) J ( 5 st , П st )

R ( 5 ⁿ • st , n n • st , 5 i , n i )J(^Пт-К^) (35)

д ² Ф + ₂ ^д5

R

+

T ( x ( 5 , , n , ), y ( 5 , , n , ), u ( 5 , n ns ), v ( 5 n ' st , n n ' st ))

^ 1 ( 5 i , n , 5 i , n , ) =

W n ( u ( 5 ⁿ • st , n n • st ), V ( 5 ^n,st , n n ' st )).

Стационарная точка находится из решения системы нелинейных алгебраических уравнений

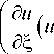
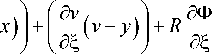
R

^ n",n ", 5,, ni) = 0(36)

д5

'? n(5-st, nn • st, 5i, ni) = o,(3

dn где

^n(5,n,5i,ni) = nФ(5,n) + R(5,n,5,,ni),(38)

R = V ( x ( ^ i , n i ) - u ( 5 , n ) ) ² + ( У ( 5 i , n i ) - V ( 5 , n ) ) ² + f ² . ⁽³⁹⁾

Предположим, что каустическая кривая формируется в основном за счет члена в разложении (34) с номером n =1. Это означает, что для точек, лежащих непосредственно на фокальной кривой (т.е. П , =О), система уравнений, определяющих стационарную точку, имеет неединственное решение. Более того, множество стационарных точек образует линию, совпадающую со слоем на фокусаторе. От-

^ 1 ⁽ 5 1 ^, n , 5 i , n , ) =

= J « ( ^{5 )} d ⁵ - f ² +n ² a ₂( 5 , ) + 1 +

^Jo V a ² ( 5 ) + 1

+ R ( 5 , , n , 5 , , n , ).

В случае, когда точка наблюдения лежит непосредственно на фокальной кривой, выражения для производных приобретают простой вид

^1(51,n,5,,0) = -J /a^5)d^,(44)

0 4a ^5) + 1

^Г(51, n, 5,,0) = ( (        1-=+

( 4a ²( 5 , ) + 1 ) V f ² +n ²

, v              ’(45)

+      a '( 5 , )                 n C ( 5 i )

(V a ²( 5 , ) + 1 )³ V a ²⁽⁵ , ) ^{+ 1} V ^{f 2} +n ²

Г ©, n , ^,0) = о,

где C ©- кривизна фокальной кривой в данной точке.

В окрестности фокальной кривой функцию ¥©, n , ^ 1 , П 1 ) с точностью до линейных членов по переменной n 1 можно представить в виде следую-

Разложение функции ^ в окрестности слоя и фокальной кривой имеет вид

щего разложения

%© n, ^, П1) = %©, n, ^1,0) + д^©, n, ^,0) „ +

+                 41 + д^

+%"©, n, ^,0)-(^Ц где д^©, n, ^1,0) = + a (^1) - dn1        V1 + a 2©)

n

V1 + a ²©) V f ² +n 2

Г| Т] ) = ^д^ ( - , ⁿ , - ,⁰¹_{п +}

1 (Ъ, 1, Ър41)                               '11 + д^

+^№ 1 , n , ^0)(^Д

Интеграл по переменной ^ легко вычисляется с помощью метода стационарной фазы [3].

Далее вычисляя интеграл по переменной n , получаем выражение для поля на фокальной кривой. В результате удалось свести вычисление двойного интеграла от быстроосциллирующей функции к вычислению однократного интеграла от гладкой функции. Полученные выражения удобно использовать для инженерных расчетов.

Пример: фокусировка излучения в тонкое кольцо

В качестве примера рассмотрим вычисление поля от фокусатора в тонкое кольцо в окрестности каустики. В этом случае фокальная кривая описывается параметрическими уравнениями

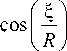
= R sin

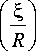
В данном случае а © = 0, и гиперболические

слои вырождаются в прямые лучи, выходящие из начала координат.

Система криволинейных координат области фокусатора имеет вид

u = ( R —n )cos

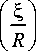
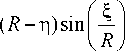
якобиан преобразования

J ⁽ n ) =

I R -3

R

Рассмотрим в разложении член с n = 1. Остальные интегралы можно вычислить с помощью метода стационарной фазы.

%"©, n , ^ 1 ,0) =

=      1 n                         (54)

V f ² +n ² R 0 V f ² +n ²

д^©, n , ^ 1 ,0) _      n

Подставляя полученные выражения в интеграл Кирхгофа-Котлера и интегрируя по переменной ^ , получаем следующее выражение для n = 1

W 1 ( ^ 1 , n 1 , f ) =

R

=1

-да

T ⁽ x ⁽ ^ 1 , n 1 ), У ⁽ ^ 1 , n 1 ), u ⁽ ^ 1 , n ), v Й1 , n )) R ( ^ 1 , n , ^ 1 0)

X W ( u ( ^ 1 , n ), v ( ^ 1 , n )) X

X,

2 n ( R -n ) У Т ²

+n

X

kR 0

exp

- ik nn 1

)

d n

Анализируя полученное выражение, отметим, что в распределение электромагнитного поля в фокальной плоскости не является радиально - симметричным и линейно поляризованным, несмотря на наличие этих типов симметрий в падающем пучке.

В параксиальном приближении f ² +n ² * f . В этом случае исчезает влияние поляризации освещающего пучка на распределение поля в фокальной плоскости вблизи фокальной кривой. Электромагнитное поле становится линейно поляризованным (при наличии линейной поляризации падающего пучка) и радиально симметричным.

В параксиальном приближении Tn (p) =5n 1, E, = H,,, E„ = H = 0 (если падающая волна линей-x yyx но поляризована вдоль оси x), и составляющая вектора Умова-Пойтинга вдоль оси распространения излучения имеет вид

9R

I ( n 1 ) = I (0)7^—;^F ( ^ ), 4( R -n 1 )

F © =

sin c

c

cos c,

?

Cl ) n ' ] c 1²Ic| J ,

^ (kP c

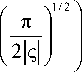
c = - kR f n 1 , I (0) = 2 kR^ f , f          9 n fR

R f - радиус фокусатора, S ( § ), C ( § ) - интегралы Френеля.

При малых п 1 из предыдущей формулы полу-

чаем

где

i (па = i (0) 1 1 - 175 с ² + о ( ^ 4 ) I .

При больших п 1

9 R

4( R -4 1 ) ^ 2

X

%4§ i , п , § i ,0) =

= ,          1 3 , --------- +                     (70)

( 4a ²( § i ) + 1 ) 4f 2 +п 2

+       a '( § i )

( 4 a ²( § i) + 1 ) ³’

5^ i ( § i , п , § i ,0 ) = + a ( § i ) п              ₍₇₁₎

54 1          4 1 + a² ( § i ) V 1 + a ² ( § i ) 4f 2 +п 2

I ( П 1 ) = I (0)

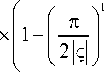
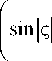
А А

⁺ cos4 ⁺ 4^J ⁺ O ⁽1 Г²⁾ .

Подставляя полученные выражения в интеграл Кирхгофа-Котлера и интегрируя по переменной § , получаем следующее выражение при n = 1

Выражение для поля вблизи фокального кольца совпадает с выражением, полученным ранее в работе [5], что подтверждает справедливость предложенного метода расчета поля в окрестности фокальной кривой.

^ ^( § 1 , п 1 , f ) =

Г Г

= exp ik Y ( § i , п , § i ,0 ) +

^{a (} § 1 ) п 1

X

Пример: фокусировка излучения в отрезок.

_X RR T ( x (§i,ni), ^y (§i,ni), ^u (§i,n), v (§₁,n)) _X -L                 R ( § 1 , п , § 1 0)

В случае фокусировки излучения в отрезок, расположенный перпендикулярно оси z , параметрические уравнения имеют вид

X W ( u ( § 1 , п ), v ( § 1 , п )) X

—L 1 x=т+§*’ у = о,

2 n 4f ² +п ² ( 4a ² ( § 1 ) + 1 ) k

X

криволинейные координаты в плоскости фокусатора имеют следующий вид

x exp

- ik пп 1 _v4^² + f 2 V 1 + a ² ( § i ) _?

u =- L + § + а ( § ) 4f 2 +П 2 ,                (63)

x^ 1 + a '(§ i ) 4 f² +п 2 | d п

v = п,(64)

криволинейные координаты в области фокусировки x = -L + §i ± а(^1)П1,

У = П1, якобиан преобразования

J (§, п) = 1 + а'(§) 4 f 2 +П2|.(67)

Разложение функции ¥ в окрестности слоя и фокальной кривой имеет вид

%( § , п , § i , П 1 ) = ^ i ( § i , п , ^ 1 ,0) +

+ ^д ^ ¹⁽ § ¹, ч , ^,0) п 1 +                          (68)

dn i

+^№ , п , § 1 ,0)-( §-§ ¹)²-,

^ i ( § i , п , § i ,0) = -J ^ ^ d L ,              (69)

0 4a ²( § ) + 1

Легко проверить, что в параксиальном приближении выражение для поля совпадает с известным выражением для интенсивности поля, представленным в работе [4].

Из приведенных примеров видно, что в обоих случаях двойной интеграл от быстроосциллирую-щей функции сводится к однократному интегралу.

3. Дифракционная коррекция фазовой функции фокусаторов в фокальную кривую

Расчет фокусаторов, приведенный в работах [2, 6] производился в приближении геометрической оптики. В этом приближении кривая представляет собой полосу, имеющую нулевую ширину. Распределение энергии в этом случае характеризуется линейной плотностью. Понятие линейной плотности является математической абстракцией и не учитывает дифракционные эффекты. В данном разделе предлагается метод расчета фокусатора в произвольную фокальную кривую, основанный на понятии интенсивности вдоль геометрической кривой. Расчет проводится на основе дифракционной аппроксимации оператора распространения для четырехмерного бивектора. При этом предполагается, что поле в плоскости, непосредственно прилегающей к ДОЭ, рассчитывается в асимптотическом

приближении. Будем также предполагать, что поле вблизи фокальной кривой формируется в основном за счет члена с n = 1 в асимптотическом разложении. Остальные члены в указанном разложении описывают дефокусированные изображения и не вносят значительного вклада в распределение интенсивности в окрестности каустической кривой, хотя и приводят к снижению контраста изображения и уменьшению дифракционной эффективности.

Пусть лазерное излучение

W ( x , y ) = I^eW₀⁺ e + I h W₀⁺ h .                    (73)

7 a ²( § 1) + 17 f ² +n ²

W ( u ( § 1 , n ), v ( § 1 , n )) =

= ( T^e ( u , v ) ( cos 9 I^е - sin 9 I h ) x

x ( PW ^{+ e} ( a 1 ,0) ) +

+ T h ( u , v )(sin 9 I^е - cos 9 I h ) ( PW ^{+ e} ( a 1 ,0) ) ) ,

падает на фокусатор [1]. Согласно методу, изложенному в предыдущем пункте, поле в фокальной плоскости вблизи фокальной кривой представляется в следующем виде

9 = arctg

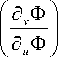
a’= cos 9 d _u Ф ( u , v ) + sin 9 d _v Ф ( u , v ),

d u Ф =

W ⁽ § 1 , П 1 , f ) = ik- ^X

4п f ( xexp ik ¥(§nn,§1,0) +      * 1

d_n v д § Ф -d § v 9_пФ J ( § , n )

X

d v ф =

d § u 8_пФ-8_п u 8 § Ф

J ( § , n )

да

x (

-да

T ^{( x (} § 1 , П 1 X У ⁽ § 1 , П 1 X u ⁽ § 1 , n X v ⁽ § 1 , n ))

V ( a ²⁽U + ¹ )( f ² +П ² )

X

Анализ полученных результатов показывает, что плотность потока электромагнитной энергии в окрестности фокальной кривой явно зависит от переменных § ₁, n ₁, a ( § ₁), a ' ( § ₁), т.е. имеет вид

x W ( u ( § 1 , n ), v ( § 1 , n )) X

2 n

X -------•-------------X

V k ^" ( § 1 , n , § 1 ,0 )

x exp

- ik nn ₁

)

■ J ( § 1 , n ) d n ,

J ( § 1 , n ) = 1 + ,----------            , x (75)

+ a '( § 1 )7 f ² +n ² -n C ( § 1 )(1 + a ²( n )),

^1(§1, n, §1,0)=4 a§dL,(76)

0 7 a ^(9 +1

%4§1, n, §1,0) =, i 1з , +

(7a2(§1) +1) 7f2 +n2 v             ’(77)

+      a '( § 1 )                 n C ( § 1)

(7 a ²(§a + 1 ) ³ 7 a ²⁽§d ^{+ 1}7 f ² +n ²

I = I ( § 1 , n 1 , a ( § 1 ), a ‘ ( § 1 )).                          (85)

Выражение (85) можно использовать для решения обратной задачи, рассматривая его как дифференциальное уравнение относительно функции a ( § ₁). Вопрос о существовании решения задачи фокусировки сводится к двум задачам:

• 1.    задача существования решения дифференциального уравнения;

• 2.    возможность восстановления функции эйконала по функции a ( § ₁).

По первому вопросу можно с определенностью сказать, что не существует в общем случае теоремы существования для нелинейных дифференциальных уравнений, не разрешенных относительно старшей производной, поэтому мы ограничимся параксиальным приближением. Предположим, что падающая волна линейно поляризована и вектор поляризации направлен вдоль оси x . В этом случае бивектор электромагнитного поля определяется только одной компонентой Е_т x

T ^{( x (} § 1 , n 1 X У ⁽ § 1 , n 1 X u ⁽ § 1 , nX v ⁽ § 1 , n ),) =

- r 0 z	0	- r 0 yr 0 x	r 20 x - 1 "
0	- r 0 z	1 - r 20 y	r 0 xr 0 y	(78)
r 0 yr 0 x	1 - r 20 x	- r 0 z	0	,
r 2 0 y - 1	- r 0 xr 0 y	0	- r 0 z _

Ex =_А Р- x )/2л f

Lf § r x exp ik - j

a ( § ) d § ± ^a ( § 1 ) n 1

7 a ²( § ) + 1 "71 + a ² ( § 1 ) J_y

„ = - a ( § 1 )7 f² +n ² X '( § 1 ) + n Y '( § 1 )

⁰ x         7 a ²(§ 1 ) +17 f ² +n ²

„ = - a ( § 1 )7 f² +n ² Y '( § 1 ) -n X '( § 1 )

⁰ y         7 a ²( § 1 ) + 17 f ² +n ²      '

x ( a ² ( § 1 ) + 1 ) x

да

X j I^е ( u ( § 1 , n ), v ( § 1 , n ) ) exp

-да

- ik nn ₁

_ч f 71 + a² ( § 1 )

x ( 1 + a ‘ ( § 1 ) f -n C ( a ² ( § 1 ) + 1 ) ) d n .

Вектор Умова-Пойтинга в этом случае пропорционален \Е_Х |².

В параксиальном приближении а ² <<1, и предыдущая формула приобретает вид

магнитных полей. Полученное выражение можно представить в виде ряда

1 1 ( § 1 ) = ^ k 7( d '( § 1 ) ) ³ x

^{9 п} f

Е _х =

X

■ ^ B 2 n + 1

'( R ² — d ²(§j ) С ( § 1 ) '

d '( § 1 )

.

г                           ( — ik nn 1

x j I ( U ( § 1 , n ), v ( § 1 , n ) ) exp I —-¹- lx        (87)

—г                              \         7

Удерживая в разложении первый член, получим

x ( 1 + a ‘ ( § 1 ) f — n C ) ^1/2 d n .

Для определения функции а ( § )получаем интегро-дифференциальное уравнение

I i ( ^ i ) =

1 1 ( § 1 ) =

= 9^7 ( d^4M ) B ² 1 ( ^R ‘ —

дифференциальное уравнение для определения функции d ( § ₁) (93)

= A

г j Ie (u(§1, П) v(§1, n))(1 + a'(^1) f—nCУ'2 dn

—г

1 1 ( § 1 ) = A ( d '( § 1 ) ) B ²1 ( R ² —

или

1261) = A x xj j Iе (u (§1, n), v (§1, n)) exp [—ik^lx,    (89)

— 8 —г                                \   7    7

x ( 1 + a '( § 1 ) f — n C ) ^1/2 d pl d П 1 ,

где A - нормировочная константа

В качестве примера рассмотрим фокусатор в произвольную фокальную кривую, имеющий круглую апертуру с радиусом , и освещаемый равномерным пучком.

В данном случае удобно ввести новую систему криволинейных координат. Связь между декартовыми и криволинейными координатами имеет вид u = d (§) X '(§) — ц Y ‘(§), (90)

с граничными условиями

d (0) = — R , d ( l ) = R .                         (98)

Уравнение разрешено относительно старшей производной, и теорема существования и единственности доказана.

Теперь для того, чтобы доказать существование решения задачи фокусировки, необходимо проверить условия корректности введения криволинейной системы координат в плоскости фокусатора. Для того чтобы ввести криволинейную систему координат, достаточно, чтобы в пределах фокусатора якобиан преобразования был отличен от нуля d'(§) + nC(§) = 0 при п2 + d2 > R2

или

C ( § ) <

d '( § )

V R ² — d ²(§)

v = d ( § ) Y '( § ) + ц Х ‘ ( § ).                       (91)

связь между новой и старой системой координат имеет вид

ц = п +

( X '( § ) X ( § ) + Y '( § ) Y ( § ) ) X ' ( § ) — X ( § ) Y ' ( § )

Следует отметить, что это условие аналогично условию отсутствия пересечения слоев в области фо-кусатора. Подставляя выражение для производной, получаем условие разрешимости задачи фокусировки

,(92)

C ( § ) <

d ( § ) = X '( § ) X ( § ) + Y'§YY ( § ) + a ( § ) f .       (93)

I ( § 1 )

/ э о \3/2 .

A ( R ² — d ²( § 1 ) )

В этом случае, вычисляя интегралы, входящие в (85), получаем

1 1 ( § 1 ) = A x

2 Г /              I \з/2

—— (d '(§1) + VR2 — d 2(§1) C(§1))   —

3C (§1) Lv’

i                1 ------------------- \ 3/2

— ( d ' ( § 1 ) — Rr ²— d ²(§j c ( § 1 ) )

Следует отметить, что условие (100) есть аналог теоремы существования, изложенной в работах других авторов [7]. В заключении распространим изложенный метод на случай, когда вместо интенсивности на геометрической фокальной кривой задана нелокальная характеристика. Пренебрегая в формуле (89) членами, содержащими произведение С п, получаем простое выражение для вычисления интенсивности электромагнитного поля вблизи фокальной кривой

Выражение представляет собой асимптотику для поля на геометрической кривой. Простой вид позволяет использовать его в инженерных расчетах для оценки качества работы фокусаторов и для тестирования численных алгоритмов расчета электро-

I ( § 1 , П 1 ) =

ck x 8п 2пf

x

j d n J ( § 1 , n )^1/2exp

I e ( § , П ) .

Рассмотрим случай, когда входной пучок имеет гауссово распределение

I^е К, n ) = exp

' -( d ²© + n2 ) '

Учитывая, что мы имеем дело с фокальными кривыми с небольшой кривизной, разложим J ( ^ _i, n )^i/2 в ряд Тейлора по степеням n C (^V d '( ^ i )

( J &, n )Г = ( d 'Ki)F 2 A n f ³^ J , (103) V d ⁽ ^ i ) J

подставляя это разложение в (101) и учитывая свойства преобразования Фурье, получим

I ^i , n i ) = c ^x i6 n f

2 An

iC &) f

d '(U k

n

I \d ' ( ^ i )exp

d X) ) d n _x

a ²

dn i n

или

xj dn exp

- iknni

f

f-n exP I —

I a

I ( ^ i , n i )

ck

--V x i6 n ² f

x

V d XUexp ^f- d-^- J D

V a J

x2 A

f iC(^,)f )n dn f n,2 ) --i— --exp —

V d '(^) k J dn _i n    V a 2 D 2 J

где D = | ff .

ka ²

При учете двух первых членов выражение приобретает вид

I Ki, n i ) =

ckd '(^) i6 n ² f ^x

x exp

2 d ²( ^ i )

a

exp

2 n i²

_a 2 _D

D ^{- i} x

( 05)

x i - A

f ic Ki) f ) 2ni

V d '( ^ ) k ^J a ² D ²

Для характеристики распределения электромагнитной энергии вдоль кривой введем нелокальную характеристику

s

0 ( ^ i , s ) = j I Ki , n i ) d n i .                        (i 06)

-s

Полагая 0 ( ^ , s )= const , получаем дифференциальное уравнение, разрешенное относительно производной.

Полученные формулы можно использовать для инженерных расчетов при оценке качества фокусировки. При c ( ^ _i) ^ 0 кривая вырождается в отрезок, и выражение переходит в формулу, приведенную в работе [8].

Заключение

В рамках электромагнитной теории впервые получены асимптотические выражения для интенсивности светового поля вблизи фокальной кривой. Приведены примеры для фокусировки в кольцо и отрезок. На основании полученных выражений предложен метод коррекции геометрооптических фазовых функций фокусаторов.