Digital IIR Filter Design using Real Coded Genetic Algorithm

Published Online June 2013 in MECS

Digital IIR filter design principally follows two techniques: transformation technique and optimization technique. Due to nonlinear and multimodal error surface of IIR filters, conventional gradient-based design methods may easily get stuck in the local minima of error surface. In order to avoid this problem efficient design methods which can achieve the global minima in a multimodal error surface are required. Genetic Algorithm (GA) is not only capable of searching multidimensional and multimodal spaces but also optimizes complex and discontinuous functions that are hard to analyze mathematically. Therefore, researchers have developed design methods based on modern heuristics optimization algorithms such as genetic algorithms [2-10], particle swarm optimization [11], seeker-optimization-algorithm-based evolutionary method [12], simulated annealing [13], tabu search [14], ant colony optimization [15], hybrid taguchi genetic algorithm (HTGA) [16],immune algorithm (TIA) [17] and many more.

Optimization methods are broadly classified based on the type of the search space and the objective function. In IIR filter design problems, the evaluation of candidate solutions could be computationally expensive since it requires time-consuming computer simulation. The normal GA design for IIR filter always assumes a predefined topology of the filter. Only the coefficients of the filter need to be determined. Genetic algorithm has been applied by Tang et al. ^[5] to design the digital IIR filters. With this method the filter can be constructed in any form, such as cascade, parallel, or lattice and also the low-pass, high-pass, band-pass, and band-stop filters can be independently designed and the classical analog-to-digital transformation is avoided.

This paper proposes an efficient real-coded genetic algorithm (RCGA) with arithmetic-average-boundblend crossover (AABX) and wavelet mutation (WM) for multicriterion optimization of digital IIR filter. The values of the filter coefficients are optimized with RCGA to achieve Lp-norm error criterion in terms of magnitude response and ripples both in pass band and stop band for multicriterion optimization problem.

The paper is organized as follows. Section II describes the IIR filter design problem statement. The real-coded genetic algorithm for designing the optimal digital IIR filters is described in Section III. In Section IV, the performance of the proposed method has been evaluated and achieved results are compared with the design results by Tang et al. ^[5], Tsai et al. ^[16] and Tsai and Chou ^[17] for the LP, HP, BP, and BS filters. Finally, the conclusions and discussions are outlined in Section V.

II. IIR Filter Design Problem

A digital filter design problem involves the determination of a set of filter coefficients which meet various performance specifications such as pass-band width and corresponding gain, stop-band width and attenuation, band edge frequencies and tolerable peak ripple in the pass band and stop-band. The traditional design of the IIR filter is described by the following difference equation:

MN y (n) = S PkX(n - k) -S q*y (n - k)            (1)

k = 0                 k = 1

where pk and qk are the coefficient of the filter. x ( n ) and y ( n ) are filter input and output. M and N are the number of filter coefficients, with N≥M.

The transfer function of IIR filter is stated as below:

H ( z ) =

M

S pkz - k k=0________

N

1+ S qkz -k k=1

To design digital filter a set of filter coefficients pk and qk are determined, which meet specified performance indices. A common way of realizing IIR filters is to cascade several first-order and second-order sections together ^[4-5]. Regardless of the filter type, the structure of cascading type digital IIR filter, is stated as [5]

and Vector x denotes the filter coefficients of dimension V×1 with V = 2M + 4N + 1 and A is the gain. The IIR filter is designed by optimizing the coefficients such that the approximation error function in L_p-norm ^{[16, 17]} for magnitude is to be minimized. The magnitude response is specified at K equally spaced discrete frequency points in pass-band and stop-band. e ₁( x ) denotes the absolute error L 1 -norm of magnitude response and e ₂( x ) denotes the squared error L₂-norm of magnitude response and are defined as given below:

K e1(x) = S|Hd (toi) - H(toi,x)l|                  (4)

i = 0

K ₂

e 2 ^{( x} ) = S ^{( H} d ^{( to} i ) - l ^{H ( to} i , x )lI)                  ⁽⁵⁾

i = 0

Desired magnitude response H ^ ( ®i -) of IIR filter is given as:

,  . _ J1, for toi e pas5band d (toi)  |o, for toi G 5topband

The ripple magnitudes of pass-band and stop-band are to be minimized, which are denoted by 5 1 ( x ) and ^ 2 ( x ) respectively. Ripple magnitudes are defined as:

51( x) = max{ Hto, x )|}-min{ H (®i, x )|} toi                    toi                          (7)

for®! e pa55band and

5 2 ( x ) = max{ H ( ®i , x )| ^{} to} i                                  (8)

for^i e 5topband

Aggregating all objectives and stability constraints, the multicriterion constrained optimization problem is stated as

Minimize f 1 ( x ) = e 1 ( x )           (9a)

Minimize f 2 ( x ) = e ₂ ( x )

Minimize f 3 ( x ) = 5 1 ( x )

Minimize J 4 ( x ) = 5 2 ( x )

ML

^H to x ) = A П

V i = 1

⁺ P 1 e

- j to ^

where

N х П V k = 1

⁺ Que - j  7

^{1 + r} 1 k e - j ® ^{+ r} 2 k e 2 j ™

1 + 5 1 k e j + ^ 1 k e ~^j

\

x = [ P 11 , ^ 11 ,-., P 1 M , 4 1M , Г 11 , r 21 , 5 11 , 5 21 ,... r 1 N , r 2 N , s 1 N ^, s 2 N ^, A ] ^T

Subject to: the stability constraints

1 + qh> 0( i = 1,2,....M)(9b)

1-qu> 0(i = 1,2,....M)(9c)

1 -52k >0(k = 1,2,....,N)(9d)

1 + 51 k + 52k >0(k = 1,2,....,N)(9e)

1 -51 k + 52k > 0(k = 1,2,....,N)(9f)

In multiple-criterion constrained optimization problem for the design of digital IIR filter a single optimal tradeoff point can be found by solving following:

Minimize f ( x ) = ^ wf ( x ) (10) j = 1

Subject to: The satisfaction of stability constraints given by (9b) to (9f). where w_j is nonnegative real number called weight.

The design of causal recursive filters requires the inclusion of stability constraints. Therefore, the stability constraints given by (9b) to (9f) which are obtained by using the Jury method [18] on the coefficients of the digital IIR filter in (3) have been forced to satisfy by updating the coefficients with random variation as given below. The variation is given as small so that the characteristic of population in RCGA should not be changed.

q i i (1 - r )²

qii = i

q _{1 i}

;(1+qn) < 0 or(1 - qn) < 0

; Otherwise

(11a)

5 2 k (1 - r )²

5 2 k = *

s _{2 k}

;(1 -52k) < 0 or(1 -52k) ^ 0

; Otherwise

(11b)

5 1 k (1 — Г )²

51 k =*

^s 1 k

; (1 + 5 1 k + 5 2 k ) <  0 or (1 - 5 1 k + 5 2 k ) <  0

; Otherwise

(11c)

where r is any uniform random number which is varied between [0,1]. Square term gives small increment.

• III.    Real Coded Genetic Algorithm

Real coded genetic algorithm represents parameters without coding, which makes representation of the solutions very close to the natural formulation of a problem. In RCGA recombination and mutation operators are designed to work with real parameters. The use of real-parameter makes it possible to use large domains (even unknown domains) for variables. Capacity to exploit the graduality of the functions with continuous variables is another advantage. In the real-coded GAs, a chromosome is coded as a finite-length string of the real numbers corresponding to the design variables. Since the crossover operator makes cuts between genes in the binary-coded GA, it changes the value of the goal function variables, while in the real-coded GA it just interchanges the variables between individuals. A comparative study conducted by [19] has concluded that the real-coded GAs outperformed binary-coded GAs in many optimization problems. The basic elements of real coded genetic algorithms are selection, crossover and mutation. In reproduction, the individuals are selected based on their fitness values relative to those of the population. In the crossover operation, two individuals are selected at random from the mating pool and a crossover is performed using mathematical relations. In mutation, an occasional random alteration of an individual is done. In this paper, a real coded genetic algorithm with genetic operators including arithmetic-average-bound-blend crossover and wavelet mutation is applied to solve the short-term fixed-head hydrothermal scheduling problem. The arithmetic-average-bound-blend crossover operator combines the arithmetic crossover, average crossover, bound and blend crossover. The arithmetic crossover operation produces some children with their parent’s features; average crossover manipulates the genes of the selected parents and the minimum and maximum possible values of the genes and bound crossover is capable of moving the offspring near the domain boundary. Therefore the offspring spreads over the domain so that a higher chance of reaching the global optimum can be obtained. The wavelet mutation operation based on wavelet theory [20] is a powerful tool for fine tuning of the genes to search the solution space locally. This property of wavelet mutation operation enhances the searching performance and provides a faster convergence than conventional real coded genetic algorithm. The above procedure to implement real coded genetic algorithm is outlined below:

Algorithm: Real coded genetic algorithm

• 1    Randomly generate initial population strings.

• 2    Evaluate fitness values of population members.

• 3    Is solution available among the population?

If ‘ yes ’ then GOTO Step 8.

• 4    Select highly fit members as parents using stochastic remainder roulette wheel selection and produce offsprings according to their fitness.

• 5    Create new member by mating current offspring’s. Apply crossover and mutation operators to introduce variations and form new member.

• 6    New members replace existing one by applying competition and selection.

• 7    GOTO Step 3 and repeat.

• 8    Stop.

• IV.    Design Examples and Comparisons

A real coded genetic algorithm with arithmeticaverage bound-blend crossover and wavelet mutation operator is applied to design the IIR filter.For the purpose of comparison, the lowest order of the digital IIR filter is set exactly the same as that given by Tang et al. [5] for the LP, HP, BP, and BS filters. Therefore, in this paper, the order of the digital IIR filter is a fixed number not a variable in the optimization process. The objective of designing the digital IIR filters is to minimize the objective function given by (10) with the stability constraints stated by (9b) to (9f) under the prescribed design conditions given in Table 1.

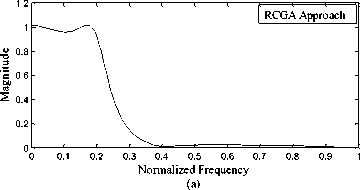
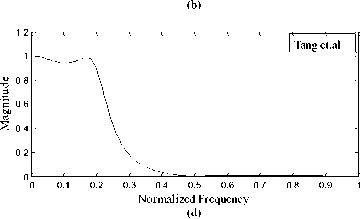
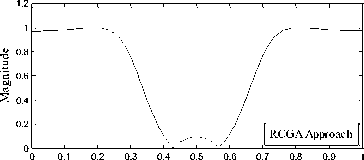
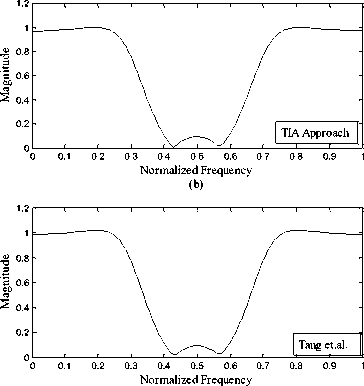
The examples of the IIR filters considered by Tang et al. ^[5], Tsai et al.^[16] and Tsai and Chou ^[17] are considered to test and compare the performance of proposed real coded genetic algorithm. For designing digital IIR filter 200 equally spaced points are set within the frequency domain [ 0, n ] . In the proposed RCGA approach the combination of four criteria, L₁ -norm approximation error, L 2 -norm approximation error, ripple magnitudes of pass-band and ripple magnitude of stop-band are considered for designing IIR filter. These four criteria are contrary to each other in most situations. The filter designer needs to adjust the weights of criteria to design the filter depending on the filter specifications. For the purpose of comparison the weights w₁, w₂, w₃ and w₄ are set to be same as in ^[17] for the LP, HP, BP and BS filters respectively. The computational results obtained by the proposed RCGA approach are presented and compared with the results obtained by ^{[5], 16].and [17]} in Tables 2,3,4 and 5 and Figures 1-4 for the LP, HP, BP and BS filters respectively. The designed IIR filter models obtained by the RCGA approach for LP, HP, BP and BS are given by (12), (13), (14) and (15) respectively.

( z + 1.1156040( z ² - 0.5927346 + 1.100357()

H_T a ( z ) = 0.04158594----------———---------------

( z - 0.63 86290( z ² - 1.3677100 + 0.7289657

(zz - 0.989191<)( z ² + 0.7097803 + 1.0503780

Hu e>( z ) = 0.05619067----------——----------------

HP               ( z + 0.614503^( z ² + 1.3455070 + 0.7274078

A 22-

H_{B p}zz ) = 0.0259320 ^ z^

- 0.269304 I z - 1.285163()( z ² + 0.2281272 z - 0.6565860 ' - 0.6371706 + 0.769549()( z ² + 0.009468 I z + 0.5415890,

x

( z ² - 0.0769073 z - 1.1026850) _v ( z ² + 0.6324920: + 0.7692200 ,

„    а        ( z ² + 0.4143518 + 0.9403490( z ² - 0.4205 842 + 0.9600804

H d c — 0.4555/58—---------------------

( z ² - 0.8350366: + 0.5427910( z ² + 0.833525 z + 0.541830)

Table 1: Prescribed design conditions on LP, HP, BP and BS filters

Filter type	Pass-band	Stop-band	Maximum Value of H ( to , x )|
Low-Pass(LP)	0 <  to <  0.2 n	0.3 n <  to <  n	1
High-Pass(HP)	0.8 n <  to <  n	0 <  to <  0.7 n	1
Band-Pass(BP)	0.4 n <  to <  0.6 n	0 <  to <  0.25 n 0.75 <  to <  n	1
Band-Stop(BS)	0 <  to <  0.25 n 0.75 <  to <  л	0.4 n <  to <  0.6 n	1

Table 2: Design results for Low Pass (LP) Filter

Method	L 1 -norm error	L 2 -norm error	Pass-band performance (Ripple magnitude)	Stop-band performance (Ripple magnitude)
RCGA Approach	4.0095	0.4185	0.9335 ≤ 1 H(ej ω ) ≤ 1.0160 (0.0825)	H ( ej ω ) ≤ 0.1510 (0.1510)
TIA Approach[17]	4.2162	0.4380	0.9012 ≤ H ( ej ω ) ≤ 1.0000 (0.0988)	H ( ej ω ) ≤ 0.1243 (0.1243)
HTGA Approach[16]	4.2511	0.4213	0 . 9004 ≤ H(ej ω ) ≤ 1 . 0000 (0.0996)	1 H ( ej ω ) ≤ 0.1247 (0.1247)
Method of Tang et al. [5]	4.3395	0.5389	0.8870 ≤ H ( ej ω ) ≤ 1.009 (0.1139)	H ( ej ω ) ≤ 0.1802 (0.1802)

Table 3: Design results for High-Pass (HP) Filter

Method	L 1 -norm error	L 2 -norm error	Pass-band performance (Ripple magnitude)	Stop-band performance (Ripple magnitude)
RCGA Approach	4.5296	0.4415	0.9677 ≤ H ( ej ω ) ≤ 1.0186 (0.0508)	H ( ej ω ) ≤ 0.1540 (0.1540)
TIA Approach [17]	4.7144	0.4509	0.9467 ≤ 1 H ( ej ω ) ≤ 1.0000 (0.0533)	1 H ( ej ω ) ≤ 0.1457 (0.1457)
HTGA Approach [16]	4.8372	0.4558	0.9460 ≤ H ( ej ω ) ≤ 1.0000 (0.0540)	1 H ( ej ω ) ≤ 0.1457 (0.1457)
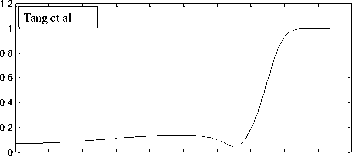
Method of Tang et al. [5]	14.5078	1.2394	0.9224 ≤ H ( ej ω ) ≤ 1.003 (0.0779)	H ( ej ω ) ≤ 0.1819 (0.1819)

Table 4: Design results for Band-Pass (BP) Filter

Method	L 1 -norm error	L 2 -norm error	Pass-band performance (Ripple magnitude)	Stop-band performance (Ripple magnitude)
RCGA Approach	1.4062	0.1961	0.9862 ≤ H ( ej ω ) ≤ 1.0050 (0. 0187)	H ( ej ω ) ≤ 0.0598 (0.0598)
TIA Approach [17]	1.6119	0.2191	0.9806 ≤ H ( e j ω ) ≤ 1.0000 (0.0194)	H ( ej ω ) ≤ 0.0658 (0.0658)
HTGA Approach [16]	1.9418	0.2350	0.9760 ≤ H ( ej ω ) ≤ 1.0000 (0.0234)	H ( ej ω ) ≤ 0.0711 (0.0711)
Method of Tang et al. [5]	5.2165	0.6949	0.8956 ≤ H ( ej ω ) ≤ 1.000 (0.1044)	H ( ej ω ) ≤ 0.1772 (0.1772)

Table 5: Design results for Band-Stop (BS) Filter

Method	L 1 -norm error	L 2 -norm error	Pass-band performance (Ripple magnitude)	Stop-band performance (Ripple magnitude)
RCGA Approach	3.7976	0.4566	0.9774 ≤ 1 H ( ej ω ) ≤ 1.0190 (0.0415)	H ( ej ω ) ≤ 0.1164 (0.1164)
TIA Approach [17]	4.1275	0.4752	0.9560 ≤ H ( ej ω ) ≤ 1.0000 (0.0440)	H ( ej ω ) ≤ 0.1171 (0.1171)
HTGA Approach [16]	4.5504	0.4824	0.9563 ≤ H ( ej ω ) ≤ 1.0000 (0.0437)	H ( ej ω ) ≤ 0.1013 (0.1013)
Method of Tang et al. [5]	6.6072	0.7903	0.8920 ≤ H ( ej ω ) ≤ 1.000 (0.1080)	1 H ( ej ω ) ≤ 0.1726 (0.1726)

1.2

0.8

0.6

0.4

0.2

0     0.1     0.2     0.3    0.4     0.5     0.6    0.7    0.8     0.9      1

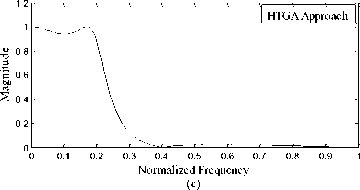
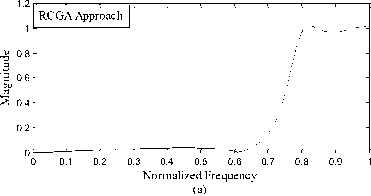
Fig. 1: Frequency responses of low pass filter using the RCGA approach and methods given in [17], [16] and [5]

Normalized Frequency

1.2

0.8

0.6

s 0.4

0.2

0     0.1     0.2     0.3    0.4     0.5     0.6    0.7     0.8     0.9      1

Normalized Frequency

(c)

0     0.1     0.2     0.3    0.4     0.5     0.6    0.7     0.8     0.9      1

Normalized Frequency (d)

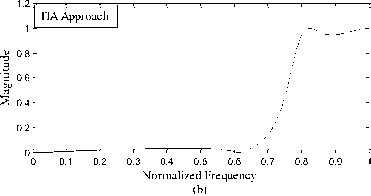
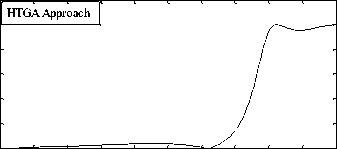
Fig. 2: Frequency responses of high pass filter using the RCGA approach and methods given in [17], [16] and [5]

1.2

0.8

0.6

0.4

0.2

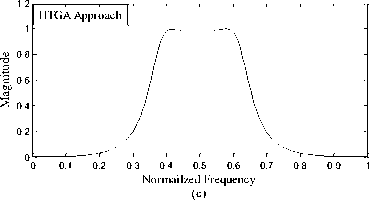
RCGA Approach

1.2

0.8

0.6

0.4

0.2

0     0.1     0.2     0.3    0.4     0.5     0.6    0.7     0.8     0.9      1

0     0.1     0.2     0.3    0.4     0.5     0.6    0.7     0.8     0.9      1

Normailzed Frequency (a)

Normailzed Frequency

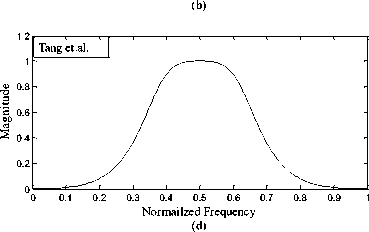
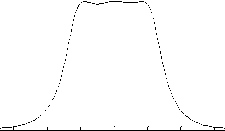
Fig. 3: Frequency responses of band pass filter using the RCGA approach and methods given in [17], [16] and [5]

Normalized Frequency

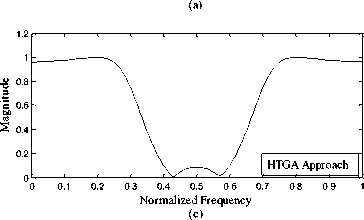
Fig. 4: Frequency responses of band stop filter using the RCGA approach and methods given in [17], [16] and [5]

(d)

• V.    Conclusion

On the basis of above results obtained for the design of digital IIR filter, we can conclude that with the proposed RCGA approach all LP, HP, BP, or BS filters can be independently designed and gives better performance in terms of magnitude approximation as compared to the GA-based methods presented by Tang et al. ^[5], Tsai et al. ^[16] and Tsai and Chou ^[17]. Summing up as shown through simulation studies RCGA proves to be a useful technique for the design of IIR filters as it satisfies prescribed amplitude specifications consistently.