Digital Image Enhancement with Fuzzy Interface System

Published Online September 2012 in MECS DOI: 10.5815/ijitcs.2012.10.06

Image can be contaminated with different types of noise, for different reasons. For example, noise can occur because of the circumstances of recording with electronic cameras, dust in front of the lens, because of the circumstances of transmission (damages data) or storage, copying, scanning, etc. [1].     Image enhancement is to improve the interpretability or perception of information in images for human viewers, or to provide `better' input for other automated image processing techniques. Image Enhancement (IE) transforms images to provide better representation of the subtle details. It is an indispensable tool for researchers in a wide variety of fields including (but not limited to) medical imaging, art studies, forensics and atmospheric sciences. Image enhancement techniques are divided into three broad categories: Spatial Domain Method Frequency Domain Method and Fuzzy Logic [2]. A fuzzy relaxation algorithm based on the second and higher order S fuzzy membership functions for the purpose of image enhancement [3].

The fuzzy set theory is incorporated to handle uncertainties (arising from deficiencies of information available from situation like the darkness may result from incomplete, imprecise, and not fully reliable, vague). The fuzzy logic provides a mathematical frame work for representation and processing of expert knowledge. The concept of if-then rules plays a role in approximation of the variables likes cross over point. Also the Uncertainties within image processing tasks are not always due to randomness but often due to vagueness and ambiguity. A fuzzy technique enables us to manage these problems effectively [4]. The fuzzy statistics are handles the inexactness of gray values in much better way compared to the classical crisp histograms thus producing a smooth histogram. The local maxima based partitioning of histogram. In the fuzzy histogram are located using the first and second derivatives [5]. Flexibility and reduction of ambiguity in decision rule are motivating factor for the use of fuzzy logic technique [6].

In this thesis the algorithm is proposed using fuzzy membership function. This algorithm enhances image contrast very effectively. Some images are not available to good quality, so proposed fuzzy algorithm can be used for image enhancement to improve the quality of images.

The remainder of this thesis is organized as follows: Section 2 gives Fuzzy Image Enhancement. Section 3 Fuzzy rule – based for Image enhancement. Section 4 presents the Proposed Algorithm. Section 5 gives Experimental Result. Conclusion & future work is given in the final section .

• II.    Fuzzy Image Enhancement

In classical or crisp set theory, the boundaries of the set are precise, thus member is determined with complete certainty. An object is either definitely a member of the set or not a member of it. However, in reality most sets and proposition are not so neatly characterized [7]. With the concept of fuzzy sets, an image X of M x N dimension and L levels can be considered as an array of fuzzy singletons, each with a value of membership function denoting the degree of having some brightness level l [8] . Fuzzy image enhancement is based on gray level mapping into a fuzzy plane, using a membership function. The aim is to generate an is image of higher contrast than the original image by giving a larger weight to the gray levels that are closer to the mean gray level of the image than to those that are farther from the mean. An image f of size M x N and L gray levels can be considered as an array of fuzzy singletons, each having a value of membership denoting its degree of brightness relative to some brightness levels. For an image f( x, y ) , we can write in the notation of fuzzy sets [9].

f (x, у) = Un xy/Ixy xy

x = 1,2,.....M and y=1,2....N           (1)

w here Ixy is the intensity of ( x , y ) th value and Ц ху is its membership value. The membership function characterizes a suitable property of image like darkness, edginess, textural property etc. and can be defined globally for the whole image or locally for its segments.[10] The basic principles of fuzzy enhancement scheme are illustrated in Fig. 1.

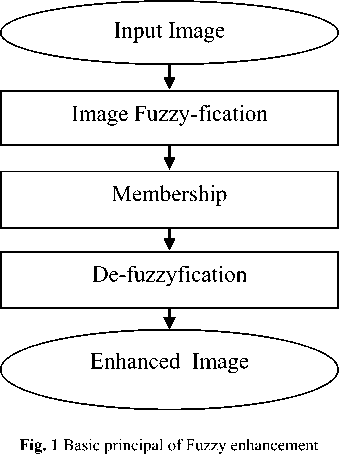
• III.    Fuzzy Rule -Based For Image Enhancement

The enhancement of an image obtained by the superposition of two complementary effects: detail sharpening and noise supersession [11]. The advantage of fuzzy interface, it balances the strength of sharpening and noise-suppression according to the properties of the input data. The first is that the image (foreground) and the background are intensity separable. A single threshold value that can separate foreground and background completely, it’s not necessary. In many case, it is vary hard to find single threshold value of the image[12].

• A.    If-then rules are three-part process:

• •    Fuzzify inputs: Resolve all fuzzy statements in the antecedent to a degree of membership between 0 and 1. If there is only one part to the antecedent, then this is the degree of support for the rule.

• •    Apply fuzzy operator to multiple part antecedents: If there are multiple parts to the antecedent, apply fuzzy logic operators and resolve the antecedent to a single number between 0 and 1. This is the degree of support for the rule.

• •    Apply implication methods: Use the degree of support for the entire rule to shape the output fuzzy set. The consequent of a fuzzy rule assigns an entire fuzzy set to the output. This fuzzy set is represented by a membership function that is chosen to indicate the qualities of the consequent. If the antecedent is only partially true, (i.e., is assigned a value less than 1), then the output fuzzy set is truncated according to the implication method.

• B.    Member Function

The only condition a membership function must really satisfy is that it must vary between 0 and 1. The function can be an arbitrary curve whose shape we can define as a function that suits us from the point of view of simplicity, convenience, speed, and efficiency. The Fuzzy toolbox includes 11 built-in membership function types. These functions are, built from several basic functions:

• •    piece-wise linear functions: The simplest membership functions are formed using straight lines.

o guess2mf: membership function is a twosided composite of two different Gaussian curves.

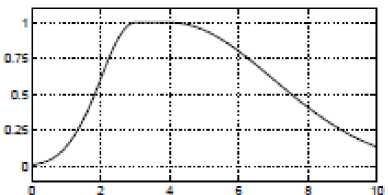
guess2mf P=[1,3,3,4]

o Trimf: the simplest is the triangular membership function, and it has the function name trimf.

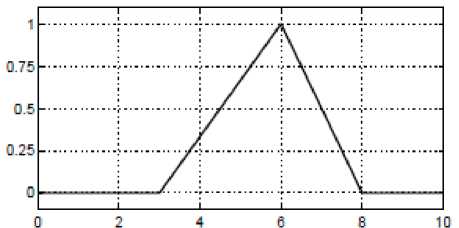
trimf, P=[3,6,8]

o gbellmf: The bell membership function has one more parameter than the Gaussian membership function, so it can approach a non-fuzzy set if the free parameter is tuned.

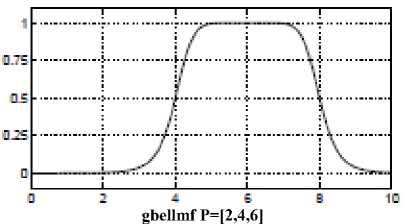
o Trapmf: The trapezoidal membership function, trapmf, has a flat top and really is just a truncated triangle curve.

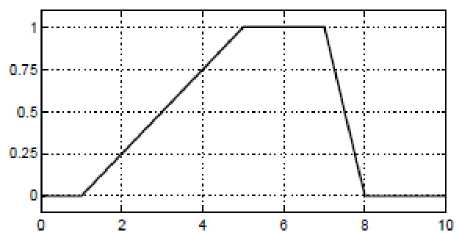
trapmf, P=[1,5,7,8]

• •    The Gaussian distribution function: membership functions are built on the Gaussian distribution curve.

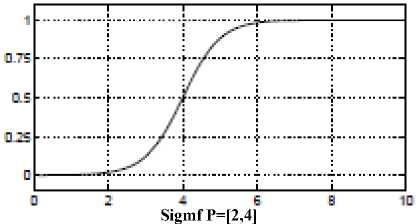
• The sigmoid curve: sigmoidal membership function, which is either open left or right.

o Sigmf:   Asymmetric and closed membership functions can be synthesized using two sigmoidal functions, so in addition to the basic sigmf.

o Guessmf: it is a simple gussen member function.

o dsigmf:  the difference between two sigmoidal functions.

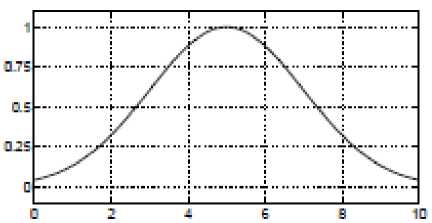
guessmf P = [2,5]

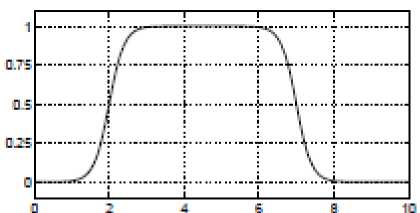
desigmf P=[5,2,5,7]

o psigmf: the product of two sigmoidal functions

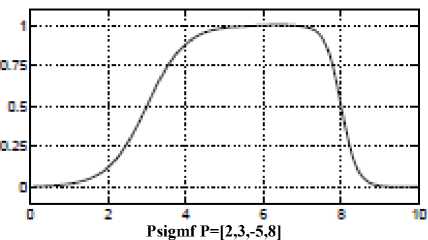
• • quadratic and cubic polynomial curves:

o zmf: is the asymmetrical polynomial curve open to the left.

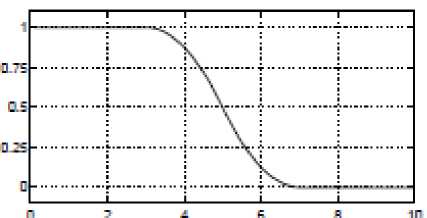
Zmf P=[3,7]

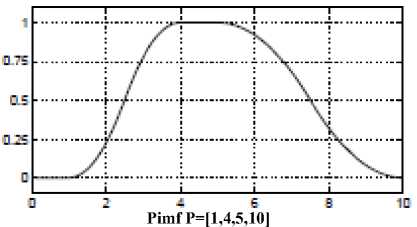
o pimf: is zero on both extremes with a rise in the middle.

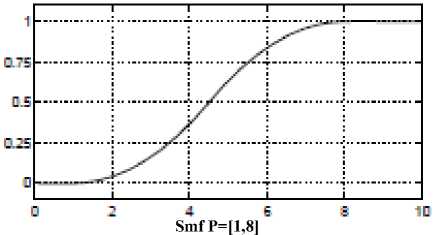
o smf: is the mirror-image function that opens to the right.

• IV.    Fuzzy Filtering (Proposed Algorithm)

This section proposes a new filtering algorithm for image enhancement method based on fuzzy interface system. The process of fuzzy inference involves all of the pieces that are described in the previous sections: membership functions and if-then rules. The following steps of an algorithm are:

• •    Read the original image.

• •    Convert it into Gray Scale image if it is RGB image.

• •    Add the noise to the image.

• •    Calculate size of original image.

• •    Perform morphological operation on image.

• •    Apply fuzzy inference Engineering.

• •    Normalization of pixel values.

• •    Passing parameters to the FIS.

• •    Compare the enhanced image with the other enhanced images.

For example, consider a 8 x 8 windows of pixel as follow:-

Table 1 Input pixel to the FIS system (8 x 8):

97	98	99	101	99	98	97	98
95	98	99	102	102	101	98	102
97	102	106	106	106	101	98	95
97	117	109	113	110	106	98	91
98	112	112	123	117	110	95	95
101	109	114	121	122	119	108	106
105	108	117	122	128	128	113	119
108	107	122	128	130	123	121	122

Table 2 Output pixel to the FIS system (8 x 8):

124	124	124	125	125	125	124	124
124	125	125	124	126	124	124	123
123	125	126	124	126	125	124	123
124	126	126	127	127	125	126	123
124	126	127	125	126	127	126	123
124	126	123	126	127	126	125	126
125	126	127	124	127	126	127	126
126	127	127	128	127	126	126	126

• V.    Experimental Result

  After designing the system we store this file into MATLAB workplace as a .fis extension. Executed this file in the Mat-Lab 2010 using the above proposed method discussed in section IV and the output of this proposed method (system) is shown in fig. 2 that the enhanced image is better than the original image.

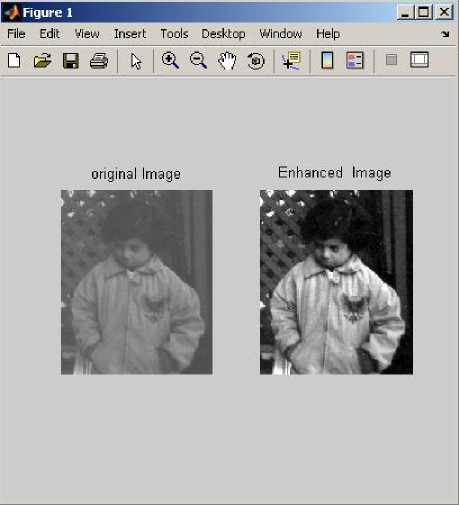
Fig 2 Enhanced image after processing original image

• VI.    Conclusion & Future Scope

The fuzzy interface system is powerful tool for formulation of expert system in a comprehensive way. The proposed technique used fuzzy if – then rules are a sophisticated bridge between human knowledge on the one side and the numerical framework of the computers on the other side, simple and easy to understand. The proposed technique is able to overcome the draw backs of spatial domain methods like thresholding and frequency domain methods like

Gaussian low pass filter. The proposed technique is able to improve the contrast of the image.

In the future the existing systems can be modified by fuzzy set theory application. Modification of fuzzy rules can produce better results. Neuro-Fuzzy techniques can be used to enhance the images.

Acknowledgment

The authors are very thankful to the reviewers and the associate editor for their remarks that helped to improve this work