Диэлектрические свойства триглицинсульфата в пористых матрицах

Многочисленные исследования, проведенные для малых частиц, выявили зависимость их физических свойств от размеров. Одним из способов получения малых частиц является внедрение исследуемого вещества в пористые матрицы, характерный размер пор которых лежит в микро-метровом или нанометровом диапазоне. Физические свойства малых частиц в таких матрицах связанны с размерами и геометрией сетки пор. Кроме того, существенную роль играют степень заполнения пористой матрицы, взаимодействие частиц со стенками матрицы и связь частиц между собой. В совокупности эти факторы приводят к тому, что характеристики частиц в ограниченной геометрии могут значительно отличаться от характеристик, как соответствующих объемных материалов, так и изолированных малых частиц.

Сегнетоэлектрические свойства частиц, введенных в нанопористые матрицы, изучены сравнительно слабо. Наибольшее количество публикаций посвящено исследованиям малых частиц нитрита натрия в порах синтетических опалов, пористых стекол и молекулярных решеток MCM-41 (см. [1-3] и ссылки в них). Имеются несколько работ посвященных сегнетовой соли и триглицинсульфата (ТГС). В частности, в [3] было обнаружено, что для пористых пленок Al₂O₃ с включениями ТГС в зависимости емкости от температуры наблюдаются два максимума. Первый из них примерно соответствует темпе ратурной области перестройки доменной струк- Трюхан Татьяна Анатольевна, аспирант кафедры теоретической и экспериментальной физики.

туры (39-41оC), второй, основной максимум, смещен относительно точки Кюри объемного монокристалла ТГС на 5-6 оC в сторону высоких температур. Сведения по исследованию ТГС в пористых матрицах другого типа, насколько нам известно, в литературе отсутствуют, поэтому целью нашей работы было исследование свойств ТГС в зависимости от типа матрицы.

ОБРАЗЦЫ И ЭКСПЕРИМЕНТ

Триглицинсульфат представляет собой классический сегнетоэлектрик с фазовым переходом второго рода и уже в течение долгого времени является объектом активных теоретических и экспериментальных исследований. Выше температуры Кюри ( Т_с = 49 ^оС) кристалл ТГС имеет моноклинную симметрию и принадлежит к центросимметричному классу 2/m. Ниже Т_с зеркальная плоскость исчезает и кристалл принадлежит к полярной точечной группе 2 моноклинной системы. Полярная ось лежит вдоль моноклинной (2-го порядка) оси b . Параметры решетки при комнатной температуре равны: a =9,15 А , b =12,69 А , c =5,73 А . На элементарную ячейку приходится более 100 атомов. Структура ТГС сложна и представляет собой сетку молекул глицина CH₂NH₂COOH и тетраэдров SO₄, связанных между собой водородными связями типа – О-H...О и N-Н.

В качестве пористых матриц в наших исследованиях использовались: фильтровальная бумага с размером пор порядка 4 мкм, окисные пленки Al₂O₃, полученные путем анодирования химически чистого алюминия в щавелевой кислоте, cо средним размером пор 100 нм и силикатные матрицы SBA-15 c размером пор 51 А . Внедрение триглицинсульфата в поры проводилось из насыщенного водного раствора. Для сравнения проводились также исследования соответствующих объемных образцов.

Для измерения электрических параметров образцов использовались цифровой измеритель импеданса E7-12 с рабочей частотой 10⁶ Гц. В качестве электродов применялась In - Ga паста. Для измерения температуры применялся электронный термометр CENTER-304 с хромель-алю-мелевой термопарой. Точность измерения температуры составляла 0,1 ^оС. Исследования проводились в температурном интервале от 20 ^оС до 100 ^оС. Для исключения влияния адсорбированной воды измерения проводились в вакууме.

ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Проведенные исследования показали, что максимум диэлектрической проницаемости для всех образцов не отличается более чем на 1-2 ^оС от температуры фазового перехода для объемного поликристаллического образца (рис. 1). Во всех матричных образцах наблюдается размытие максимума е' ( Т ) , которое определяется не размерами пор, а степенью упорядочения матрицы. Наибольшее размытие е ' ( Т ) имеют образцы из фильтровальной бумаги, где наибольший разброс по размерам и направлениям пор. Меньшую ширину фазового перехода имеют образцы из окисной пленки Al₂O₃, и еще меньшая ширина е '( Т ) для силикатных матриц SBA-15, где размеры пор калиброваны с точностью до 0,1 Å .

Для образцов ТГС в силикатных матрицах SBA-15 кроме уширения фазового перехода наблюдается активационный рост е ' ( Т ) с ростом температуры (рис. 2), что можно объяснить ионно-миграционной поляризацией за счет увеличения числа ионов принадлежащих поверхности.

Для понимания незначительного изменения температуры фазового перехода при уменьшении размера пор обратимся к теории ГАК (Гинзбурга-Андерсона-Кохрэна), где природа сегнетоэлектричества связывается с существованием в кристалле низкочастотного температурно-зависимого поперечного оптического колебания “мягкой моды”.

При сокращении размеров кристалла в одном, двух или трех измерениях (пленка, нить, сфера) из-за отсутствия трансляционной симметрии при анализе динамики решеточных колебаний нельзя уже использовать циклические условия Борна-Кармана. Последние должны быть заменены граничными условиями на поверхности. В результате, прежде всего не реализуются длинные волны с Я2 > d (q < Пd) , где d — меньший размер кристалла, а q = 2п/Я — волновой вектор [4]. В обычных кристаллах оптические ветви LO и ТО почти не имеют дисперсии и на них такое отсечение почти не влияет. В сегнетоэлектриках, благодаря большой роли даль- нодействующих кулоновских сил, частота ветви ТО для длинных волн резко падает и размер d может существенно влиять на спектр решеточных колебаний. Последнее приводит к тому, что при определенных размерах частиц длинноволновые колебания не возникают и сегнетоэлектрические свойства уже не будут реализоваться.

Строго говоря, приведенные выше выводы получены: во-первых, для изолированных сегнетоэлектрических частиц; во-вторых, для веществ, где “мягкая мода” имеет малое затухание. Для сегнетоэлектриков типа порядок–беспорядок, сегнетоэлектрическое колебание имеет релаксационный характер с большим коэффициентом затухания, и говорить о длине волны и граничных условиях не совсем корректно.

Из вышеизложенного можно предположить, что в сегнетоэлектриках типа ТГС механизм, связанный с ограничением длинны волны “мягкой моды”, не будет иметь место, хотя остаются механизмы, связанные с изменением соотношения количества атомов в объеме и на поверхности, механическим зажатием нанокристаллов в порах и т.д.

Размытие фазового перехода является общим свойством всех сегнетоэлектрических кристаллов при увеличении концентрации дефектов. Это раз-мытие означает, что в сильно дефектных кристаллах сингулярность в по-ведении материальных констант исчезает. По-видимому, это связано с тем, что в таких кристаллах фазовый переход при температуре T _о, происходит не по всему объему образца, а появляется некото--рое распределение локальных температур перехода, значения которых зависят от распределе-

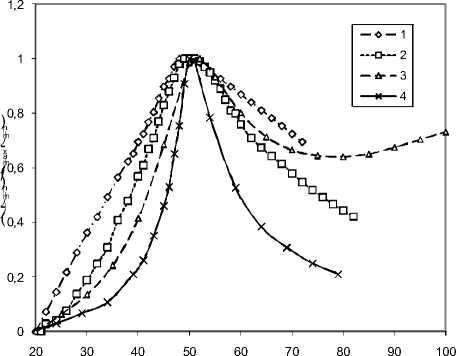
t, oC

Рис. 1. Температурная зависимость относительного изменения диэлектрической проницаемости для ТГС в различных матрицах: 1 - фильтровальная бумага ( и 4 мкм), 2 - пористая пленка A12O3 ( U 100 нм), 3 - силикатная матрица SBA-15 ( и 5,1 нм), 4 – прессованный объемный ТГС ния дефек-тов по различным локальным областям кристалла [5].

Размытие фазового перехода можно объяснить и в рамках феноменологической теории Ландау - Гинзбурга [6]. Вклад в плотность свободной энергии сегнетоэлектрика, обусловленный поляризацией Р , может быть представлен в виде:

F = 2 a P ² + 4 P P ⁴ + 6 Y P ⁶ - EP , a = a (T - T o ), (1) где a ₀, в , Y - температурно-независимые коэффициенты Ландау, Т _о – температура Кюри. Отметим, что при в >  0, Y ^ 0 (1) описывает фазовый переход второго рода, а при в <  0, Y >  0 -переход первого рода.

Разложение Ландау для плотности свободной энергии неоднородной системы содержит не только различные степени параметра порядка, но также и производные от параметра порядка по координатам. В случае идеали-зированной изотропной системы первые производные параметра порядка могут входить в разложение только в виде скалярной комбинации (grad P )², и поэтому мы можем в самом общем виде записать [7]. F ( P r ), T ) = 2 « Т^ ( r ) + 4 вП ^ + ^ S T) ( grad P ( r ) ) ² - EP (2)

Используя вариационный подход и минимизируя свободную энергию (2), можно найти уравнение состояния в электрическом поле:

E=ao (T - To) P(r)+Mr)+23(T) (APr)). (3)

Чтобы получить диэлектрическую восприимчивость X , нам необходимо найти производную по поляризации от соотношения (3):

/' = dE = a o (T - T o ) + 3 P B 2 ( r ) + 2 5 (T)d ( A P ( r ) ) . (4)

Или ограничиваясь, первыми членами разложения, и выражая, диэлектрическую проницаемость получим:

( T ) « 1 +------------------------ f 51

^V "      a o ( T - T o ) + f ( P ( r , T)) ,     ⁽⁵⁾

где f ( P ( r ), T ) = 2 5 (T ) dP ( A P ( r , T ) ) .

Из вышеизложенного следует, что для неоднородных систем в знаменателе закона Кюри-Вейсса появляется дополнительное слагаемое, приводящее к размытию кривой Р ( Т ) . Степень размытия будет определяться неоднородностью композита матрица-сегнетоэлектрик, которую проблематично выразить в общем виде, т.к. она зависит от распределения поляризации по образцу.