Dimensionality reduction for classification and clustering

Published Online April 2019 in MECS

Thanks to the advancements in information and communication technology, data are generated massively from different sectors such as medical, education, commercial, etc. These data are processed for making decision. The classification and clustering tasks are carried out to make data-driven decisions. These decisions are used to improve the quality of service or production process in various sectors. In general, the clustering and classification algorithms build the predictive model based on the data. Then, these predictive models are used to predict the unknown data from the known data. If the size of the data is large, the classification and clustering algorithm take more time to build the predictive model. Moreover, the large size of the data reduces the accuracy of the predictive model. Hence, the size of the data can be reduced using dimensionality reduction method. This method is also known as feature selection or variable selection.

Variable selection is classified into three types namely wrapper, filter and embedded methods. The wrapperbased variable selection method generates the possible variable subsets from a dataset and each subset is evaluated using any one of the classification algorithm. Based on the merit of the evolution a particular variable subset is selected as significant variable subset for classification or clustering task. The wrapper-based variable selection produces higher accuracy for classification tasks. It does not possess high generality since it produces higher accuracy only for the classification algorithm that is used for the variable subset evaluation. Computational complexity is more since it uses the classification algorithm for the evaluation of the variable subsets. The filter-based variable subset selection selects the significant variable subsets from the dataset using any one of the statistical measures. The computational complexity is less since it does not use any classification algorithm to evaluate the variable subsets. It possesses high generality since it does not use classification algorithm for the variable selection process. In the embedded-based variable selection method a part of the classification algorithm is used to evaluate the significance of the variables. It does not possess high generality since it uses classification algorithm and also it produces higher accuracy only for the classification algorithm which was used for variable selection process. The computation complexity of embedded-based method is lesser than the wrapper-based method and it is higher than the filter-based method.

In general, the accuracy in prediction determines the quality of the data-driven decision making. Therefore, improving the accuracy of the classification and clustering algorithm is the prime task of the researchers to carry out accurate prediction in data-driven decision making. Hence, this paper presents a wrapper-based variable selection method to improve the accuracy of classification and clustering algorithms.

The rest of this paper is organized as follows: Section II presents the related work. Section III presents wrapper- based variable section. Section IV discusses the experimental setup and experimental procedure. Section V discusses the results. Section VI concludes the paper.

• II.    Related Works

This section presents the review on the research works that are carried out by various researches related to the proposed research work. The classification task is carried out for recognition, prediction, and identification of the objects or data. The clustering tasks can be used to identify or predict the group label of the objects. The classification and clustering tasks are carried out in several domains for vide range of applications. For example, in medical, the classification task is used to diagnose the disease of the patient. In commercial applications, the classification task is performed to predict the buying behavior of the customers, genuine of the currency notes, etc. The clustering task is carried out in many sectors. For example, the clustering tasks are carried out for outlier detection in social networks to detect the intruders or unethical behavior groups. In a manufacturing unit, the outlier detection is used for identifying the defective components, etc. Therefore, there is a pressing need to improve the accuracy of clustering and classification. Improving the accuracy in classification and clustering can be achieved by dimensionality reduction methods. Hence, many researchers are involved in developing suitable dimensionality reduction methods to improve the accuracy in the classification and clustering algorithms.

In the recent past, face recognition is widely used for authentication and to provide security. Therefore, many researchers carry out the dimensionality reduction for face recognition application. Lina Liu et al presented a dimensionality reduction with locality constrained dictionary learning approach for data classification. This method is used for gender classification, face identification, and object recognition [1]. Sen Yuan et al. proposed a method known as multi-linear spatial discriminant analysis (MSDA) for dimensionality reduction. Using this method, the classification accuracy for face recognition is improved [2]. Moreover, Qiang Yu presented Euler- locality preserving projection (LPP) approach for dimensionality reduction and the experiment is conducted on the face dataset [4]. Furthermore, Min Jiang presented a dimensionality reduction approach to improve accuracy in classification. The face dataset is used to conduct the experiment [7].

Some of the researchers try to improve the classification accuracy in hyper-spectral data. Xuesong Wang et al. presented a dimensionality reduction method based on nonnegative sparse divergence and pairwise constraint discriminative analysis for improving accuracy in hyperspectral data classification [3] and Yanni Dong developed a dimensionality reduction method for improving accuracy for hyper-spectral image classification. In this method, locally adaptive dimensionality reduction metric is used for dimensionality reduction [6].

The classification algorithm is also used for detection of software fault and software vulnerability. Jeffrey Stuckman et al. investigated the effect of dimensionality reduction in predicting the software vulnerability [5]. Furthermore, some of the researchers concentrated on improving the accuracy in recognition and clustering tasks using dimensionality reduction. Changqing Zhang presented an unsupervised dimensionality reduction for improving accuracy in recognition and clustering tasks [8]. Dominik Sacha presented a dimensionality reduction approach [9]. Junli Liang presented a dimensionality reduction approach for tensor data recognition [10]. Moreover, D. Singh et al. developed a dimensionality reduction method for medical diagnosis [11].

• H. B. Kekre et al described a dimensionality reduction method for content-based image retrieval (CBIR). However, the histogram-based feature extraction framework is used for variable reduction. In order to evaluate the presented work, the performance evaluation metrics such as precision, recall and length of string to retrieve all relevant images are used [12].

Ah. E. Hegazy et al proposed a dimensionality reduction approach using an improved whale optimization for data classification. The performance of this proposed method is compared with the different optimization techniques such as standard whale optimization, antlion optimization, genetic algorithm and particle swarm optimization [13].

Micheal O. Arowolo et al explored a hybrid dimensionality reduction approach to classify the microarray data. Moreover, the performance evaluation metrics such as time taken for training, accuracy, sensitivity, specificity, precision, area under curve and error are used to justify the performance of the proposed system [14].

Shilpa Sharma et al presented a dimensionality approach using the principle component analysis for recognize the hand sign [15]. Amir Enshaei et al presented a dimensionality reduction using the targeted projection pursuit technique [16].

Masoumeh Zareapoor et al used the dimensionality reduction method to classify the text documents [17]. Asir et al presented a feature ranking method for reducing the dimensionality to improve the accuracy of the classification algorithms [18]. Asir et al proposed a dimensionality reduction method using the rough set theory in order to improve the classification accuracy [19].

From the literature, it is observed that the dimensionality reduction removes the irrelevant and redundant variables from the training data so that the significant variables are obtained to develop the highly accurate classification or clustering models. Moreover, the dimensionality reduction is a tool to improve the accuracy of classification and clustering tasks. Therefore, this paper presents a wrapper-based dimensionality reduction approach to improve the accuracy of classification and clustering tasks.

• III.    Wrapper-Based Dimensionality Reduction

This section presents a wrapper-based dimensionality reduction approach. In the wrapper-based approach the classification algorithm is used to select the significant variable subset from the dataset. The algorithm of the wrapper-based approach is presented in Algorithm 1.

Algorithm 1: Wrapper-based dimensionality reduction

Input: Dataset with all variables D = {V 1 , V 2 , V 3, _,V N } Output: Selected set of variables D _ss = {V 1 , V 2 , V ₃,...,V_n }

Where, D, V and D represent the dataset, variables and selected variable subset respectively. N represents total number of variable in D. n represents total number of variables selected from D.

Step 1: Begin

Step 2: Read the dataset D

Step 3: Perform searching to form the variable subset

Step 4: Evaluate variable subset using classification algorithm

Step 5: If the selected subset does not meet the criterion go to Step 4 otherwise go to Step 6

Step 6: Select the best variable subset

Step 7: End

• IV.    Experimental Setup and Experimental Procedure

  The experiment is conducted using the Weka software [20] with the computer system configuration of Windows 7 Professional 64-bit Operating system, Intel(R) Core(TM) 2 CPU T5300 @ 1.73 GHz Processor, 4.00 GB RAM and 300 GB Hard disk. The experiment is conducted with 10 well-known publically available dataset from various domains, collected from the Weka dataset repository. The details of datasets are presented in Table 1.

• A.    Experiment1: Dimensionality Reduction for Classification Algorithm

The Fig. 2 shows the experimental procedure for the dimensionality reduction for classification algorithm. Initially, the dataset is given to the dimensionality reduction algorithms namely correlation-based feature selection (CFS) and the wrapper-based method namely wrapper-based feature selection with naïve Bayes classifier (W-NB), wrapper-based feature selection with OneR classifier (W-OR), wrapper-based feature selection with random forest classifier (W-RF). Then, the variables of the dataset are reduced.

Dataset with full variables

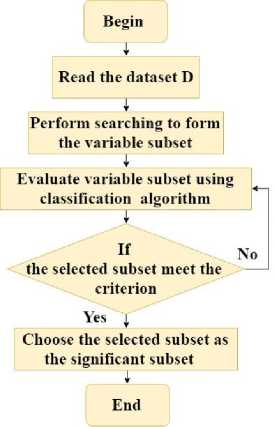
Fig.1. Flowchart representation of Wrapper-based dimensionality reduction

Dimensionality reduction algorithm

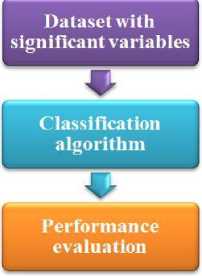
Fig.2. Flowchart representation of Experiment1: Dimensionality Reduction for Classification Algorithm

Algorithm 1 and Fig. 1 presents the wrapper-based dimensionality reduction. This algorithm receives the dataset with all variables D= {V 1 , V 2 , V 3 ,_,V N } and produces the selected set of variables D ss = {V 1 , V 2 , V ₃ ,...,V _n } is received as the output. Initially, the dataset is read and searching is performed on the dataset to generate the variable subsets. Then the variable subsets are evaluated using the classification algorithm. If the evaluated variable subset meets the criterion then that variable subset is selected as the significant variable subset.

Then the reduced variable dataset is given to the respective classification algorithms. In this paper, three classification algorithms are used to validate the dimensionality reduction methods namely naïve Bayes classifier (NB), OneR classifier (OR), and random forest classifier (RF). Moreover, the correlation-based feature selection (CFS) and the classifiers that are used in this paper are described as follows:

Correlation-based feature selection (CFS): This approach initially generates the number of possible variable subsets from the given dataset. Then, each subset is evaluated using the correlation measures with the statement of “The variables of a best variable subset have high correlation with the class attribute and have low correlation among the variables that are present in the variable subset” [21].

Naïve bayes classifier (NB): The NB classifier fundamentally belongs to the category of probabilisticbased classification approach. The naïve Bayes probabilistic method is used in classification algorithm to develop the classification model. In this classification approach, it is assumed that the values of the different variables that are present in the dataset are independent. This classification approach is used for various real-world applications in order to solve the classification problems. Moreover, the NB classifier estimates the parameters that are used to classify the unknown class label of the given instance by even small number of training data [22].

OneR classifier (OR): The OR classification algorithm is known as “one rule” classification algorithm. This algorithm generates one rule for each variable that are present in the dataset and selects the rule which one is minimum error among the other rules to perform the classification task [23].

Random forest classifier (RF): The random forest algorithm uses the decision trees to construct the classification model. The forest is refereed as a set of decision trees used for improving the predictive accuracy [24].

• B.    Experiment 2: Dimensionality Reduction for Clustering Algorithm

The Fig. 3 shows the experimental procedure for the dimensionality reduction for clustering algorithm. Initially, the dataset is given to the dimensional reduction algorithms namely wrapper-based feature selection with naïve Bayes classifier (W-NB). Then, the variables of the dataset are reduced. Then the reduced variable dataset is given into the k-means clustering algorithm with different number of clusters.

Table 1. Details of the dataset

Dataset	Variables	Instances	Classes
Breast-Cancer	9	289	2
Contact-Lenses	4	24	3
Credit-G	20	1000	2
Diabetes	8	768	2
Glass	9	214	7
Ionosphere	34	351	2
Labor	16	57	2
Segment	19	1500	7
Soybean	35	683	19
Vote	16	435	2
Average	17	7.4	5.9

Dataset with full variables

Dimensionality reduction algorithm

Dataset with significant variables

Clustering algorithm

Performance evaluation

Fig.3. Flowchart representation of Experiment1: Dimensionality Reduction for Classification Algorithm

K-means clustering: This clustering algorithm randomly chooses the k numbers of data points from the dataset to form the k number of clusters. Initially, the chosen k data points are considered as the cluster center and the distance between the cluster center and other data points are calculated in an iterative manner. Then, the cluster center is changed iteratively for forming the perfect clusters [25] [26].

• V.    Results and Discussion

This section presents the experimental results. Table 2 and Figure 4 show the total number of variable (WO) of the dataset and the number of variables in the reduced dataset by the dimensionality reduction methods. Table 3 and Figure 5 show the classification accuracy of naïve Bayes (NB) classifier with total number of attributes and different dimensionality reduction techniques. Table 4 and Figure 6 show the classification accuracy of OneR classifier (OR) with total number of attributes and different dimensionality reduction techniques. Table 5 and Figure 7 show classification accuracy of random forest classifier (RF) with total number of attributes and different dimensionality reduction techniques. Table 6 shows the sum of squared errors of clustering with different number of clusters respect to total number of attributes and different dimensionality reduction techniques for various dataset. Figure 8 shows sum of squared errors of clustering with different number of clusters respect to total number of attributes and different dimensionality reduction techniques for the dataset Breast Cancer. Figure 9 shows sum of squared errors of clustering with different number of clusters respect to total number of attributes and different dimensionality reduction techniques for the dataset Glass. Figure 10 shows sum of squared errors of clustering with different number of clusters respect to total number of attributes and different dimensionality reduction techniques for the dataset Ionosphere.

Table 2. Number of variable with respect to the wrapper methods

Dataset	WO	CFS	W+NB	W+OR	W+RF
Breast-Cancer	9	5	2	1	2
ContactLenses	4	1	2	1	2
Credit-G	20	3	12	1	3
Diabetes	8	4	5	1	7
Glass	9	8	2	1	5
Ionosphere	34	14	5	1	15
Labor	16	7	5	1	16
Segment	19	6	6	1	7
Soybean	35	22	17	1	15
Vote	16	4	3	1	7
Average	17	7.4	5.9	1	7.9

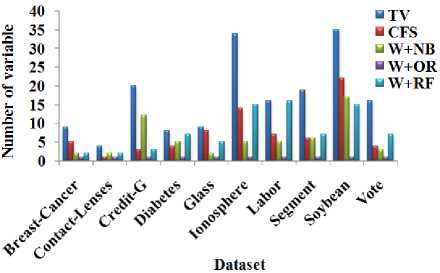
Fig.4. Number of variable with respect to the wrapper methods

Table 3. Classification accuracy of naïve Bayes (NB) classifier with total number of attributes and different dimensionality reduction techniques

Dataset	WO	W+NB	CFS
Breast-Cancer	71.67	75.17	72.37
Contact-Lenses	76.15	87.50	82.49
Credit-G	75.40	76.10	74.40
Diabetes	76.30	77.73	77.47
Glass	48.59	58.87	47.66
Ionosphere	82.62	91.45	92.02
Labor	89.47	89.47	91.22
Segment	81.06	88.06	81.73
Soybean	92.97	93.85	92.24
Vote	90.11	96.32	96.09
Average	78.43	83.45	80.76

From Table 2 and Fig. 4, it is observed that W+OR significantly reduces the number of variable from the datasets and W+NB reduces more number of variables from the dataset than the CFS and W+RF. From Table 3 and Fig. 5, it is observed that W+NB produces better accuracy compared to other dimensionality reduction methods in terms of average accuracy.

Fig.5. Classification accuracy of naïve Bayes classifier (NB) with total number of attributes and different dimensionality reduction techniques

Table 4. Classification accuracy of OneR classifier (OR) with total number of attributes and different dimensionality reduction techniques

Dataset	WO	W+OR	CRF
Breast-Cancer	65.73	72.37	65.73
Contact-Lenses	70.83	70.83	70.83
Credit-G	66.10	71.70	71.1
Diabetes	71.48	71.48	71.48
Glass	57.94	57.94	57.94
Ionosphere	80.91	82.62	80.91
Labor	71.92	77.19	77.19
Segment	64.26	65.00	64.26
Soybean	39.97	39.97	36.60
Vote	95.63	95.63	95.63
Average	68.47	70.47	69.16

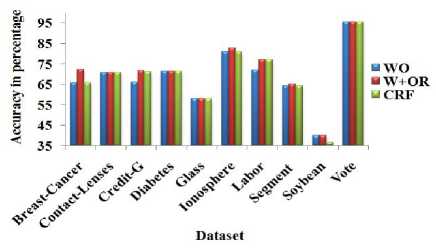
Fig.6. Classification accuracy of OneR classifier (OR) with total number of attributes and different dimensionality reduction techniques

Table 5. Classification accuracy of random forest classifier (RF) with total number of attributes and different dimensionality reduction techniques

Dataset	WO	W+RF	CFS
Breast-Cancer	69.58	75.17	70.62
Contact-Lenses	70.83	83.33	62.50
Credit-G	76.40	73.90	70.20
Diabetes	75.78	76.17	74.73
Glass	79.90	78.50	79.90
Ionosphere	92.87	95.15	94.87
Labor	89.47	85.96	87.71
Segment	97.86	98.00	98.13
Soybean	92.97	93.26	94.28
Vote	96.09	95.86	96.09
Average	84.17	85.53	82.90

Table 6. Sum of squared errors of clustering with different number of clusters respect to total number of attributes and different dimensionality reduction techniques for various dataset

Dataset		Number of clusters
		2	3	4	5	6	7	8	9	10
BreastCancer	WO	1177.00	977.00	932.00	888.00	847.00	826.00	798.00	800.00	766.00
	W+NB	0191.00	120.00	100.00	067.00	045.00	033.00	025.00	018.00	000.00
	CFS	0553.00	479.00	444.00	443.00	430.00	422.00	386.00	365.00	351.00
Glass	WO	0118.20	077.12	075.33	066.13	052.18	049.94	048.47	048.04	038.47
	W+NB	0075.51	044.99	043.98	042.33	029.52	041.20	028.95	012.27	028.46
	CFS	0118.97	073.14	070.58	061.39	048.43	046.19	045.15	035.49	035.35
Ionos phere	WO	0726.10	698.25	585.51	537.73	518.41	512.51	492.88	466.82	452.85
	W+NB	0210.64	201.97	082.00	076.90	075.67	075.05	074.63	063.33	054.16
	CFS	0302.91	263.11	254.00	242.02	235.37	227.92	207.80	214.86	196.37

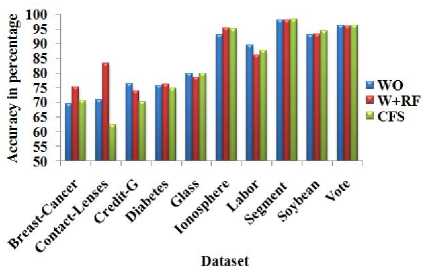
Fig.7. Classification accuracy of random forest classifier (RF) with total number of attributes and different dimensionality reduction techniques

The full set of variables (WO) produce the accuracy equal to the W+NB for the Labor dataset. However, the W+NB reduces the 25% of the features from WOW+NB produces better accuracy with NB for more number of datasets than CFS. From Table 4 Fig. 6, it is observed that W+OR produces better accuracy compared to other dimensionality reduction methods in terms of average accuracy. W+OR produces better accuracy with NB for more number of datasets than CFS. Table 5 and Fig. 7 reveals that W+RF produces better accuracy compared to other dimensionality reduction methods in terms of average accuracy.

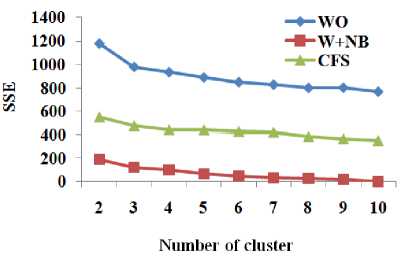
Fig.8. Sum of squared errors of clustering with different number of clusters respect to total number of attributes and different dimensionality reduction techniques for the dataset Breast-Cancer

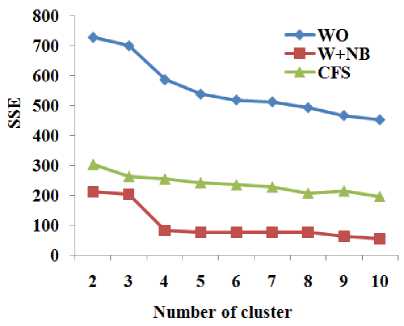
Fig.10. Sum of squared errors of clustering with different number of clusters respect to total number of attributes and different dimensionality reduction techniques for the dataset Ionosphere

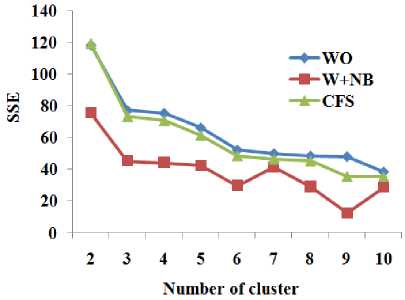
Fig.9. Sum of squared errors of clustering with different number of clusters respect to total number of attributes and different dimensionality reduction techniques for the dataset Glass

W+RF produces better accuracy with the RF for more number of datasets than CFS. From Table 6 and Fig. 8 to Fig. 10, it is obvious that W+NB reduces the sum of squared errors of clustering with different number of clusters compared to WO and CFS for the datasets Breast-Cancer, Glass and Ionosphere. Hence, the wrapper-based methods produce higher classification accuracy with the classification algorithms and reduce the sum of squared errors for the clustering algorithms.

• VI.    Conclusion

This paper presented the wrapper-based dimensionality reduction method for classification and clustering. The presented wrapper-based methods namely wrapper-based feature selection with naïve Bayes classifier (W-NB), wrapper-based feature selection with OneR classifier (W-OR), and wrapper-based feature selection with random forest classifier (W-RF) produce better accuracy for the classification algorithms. Moreover, the wrapper-based dimensionality reduction method W-NB reduces the sum of squared errors compared to other methods. For the extension of this work, different types of classification algorithms can be incorporated with the presented approach.