Динамическая и статическая космологическая постоянная в семимерных гравитационных уравнениях

В общей теории относительности вводится физическая величина. - космологическая постоянная, которая характеризует свойства вакуума. Впервые космологическая постоянная появляется в трудах Альберта Эйнштейна с целью получения однородного статического решения в космологии [1]. Однако после построения Александром Фридманом теории динамической Вселенной и получения подтверждающих наблюдений необходимость в космологической постоянной отпала. [2].

В лекции Д. Гросса. "Грядущие революции в фундаментальной физике"говорилось, что до 1997 года достоверных указаний па отличие космологической постоянной от пуля не было [3], поэтому опа рассматривалась в общей теории относительности как необязательная величина, наличие которой зависит от эстетических предпочтений автора. Величина космологической постоянной меньше чем 10-29 г/см3, что позволяет пренебрегать эффектами, связанными с ее наличием, вплоть до масштабов скоплений галактик, то есть практически в любой рассматриваемой области, кроме космологии [4]. В космологии наличие космологической постоянной может существенно изменять некоторые этапы эволюции наиболее распространенных космологических моделей. В 1998 году двумя группами астрономов, изучавших сверхновые звезды, практически одновременно было объявлено об открытии ускорения расширения Вселенной, которое объясняется теорией с ненулевой космологической постоянной [5], [6]. К настоящему времени эта теория хорошо подтверждена, наблюдениями WMAP [7]. Величина космологической постоянной соответствует плотности энергии вакуума. 5, 98 • 10-10 Дж м3.

Но, если в уравнениях Эйнштейна, для четырехмерного пространства-времени, введение космологической постоянной зависит от эстетических предпочтений автора, или из данных наблюдений a posteriori, то в работе [8], для пространств больших размерностей n > 4, космологическая постоянная необходима для выполнения закона сохранения. С другой стороны, в работе [9] показано, что для объяснения динамики не только поступательного, по и вращательного движения тел можно использовать семимерпое пространство-время. Применяя подобную концепцию, автор получает гравитационные уравнения которые также содержат космологическую постоянную, вводимую из соображений равенства между тензором кривизны и тензором энергии-импульса.

Основная часть

Для определения положения твердого тела в пространстве необходимы три координаты центра, тела x, y, z и три угла Эйлера ориентирующие тело в пространстве у - угол собственного вращения, ф - угол прецессии. 9 - угол нутации. Тогда, совокупиость координат события (t, x, y, z, ^, ф, 9) будет полностью описывать положение любого твердого тела в пространстве-времени. В результате уравнения геодезических в семимериом пространстве-времени будут описывать не только поступательное движение, по и дадут уравнения гироскопов, описывающих вращательное движение, см. [9], [10], [11].

При отсуствии материи в имеет вид [11]:

семимериом пространстве-времени метрика несимметричного тела.

9oo = 1, gaa = — 1,

944 = — -, m

~ = ~ = I4 cos 9

45    54

(I4 (sin ^)2 + I5(cos ^)2)(sin 9)2 + I4(cos 0)2

~    ~      (I4 — I5 )sin 9 sin у cos у g56   g65

~ =  I4(cos y)2 + /5(sin y)2

где I4, I5, I 6 - моменты инерции пробного тела относительно осей вращения, прецессии и нутации, m - масса тела, а пробегает значения 1, 2, 3. В той же работе [11] показано, что гравитационные уравнения в семимериом пространстве-времени принимают вид:

R mn

— Ж ^Tmn

2 g mn T^ +^Лтп,

где Л_тп - дополнительный тензор. Введение Л_тп необходимо по той причине, что не все компоненты R_mn для метрики (1) в отсутствии материи T mn = 0 обращаются в ноль. Находя альтернативную форму записи уравнений (2) нетрудно получить:

R mn  5 g mn R  ^жТтп + А mn ,

где тензор Amn равен:

^A mn ^Л тп   5 ^д тп ^Л.

Его можно трактовать как некоторую нулевую энергию вакуума:

-        1

Tmn  “ Amn.

Ввиду независимости тензора энергии-импульса нулевой энергии А_тп от времени в дальнейшем будем его называть статической космологической постоянной.

Расчет значений компонент тензора нулевой энергии T_mn, для метрики (1) приводит к следующим компонентам тензора энергии-импульса пустого пространства:

2^00 = _—T¹¹ = -2^22 = -2^33 = m ^(2I4I5 ^— I4 ^{+ 2I}4I6 ^— I5 ^{+ 2I}5I6 ^— I6 ) Ж                4I4I5I6

Сопоставим полученные значения (6) с тензором энергии-импульса для идеальной жидкости:

mn

T^mn = (ec² + p) —— — g^mnp. c²

Подставляя значение компонент метрики (1) и сравнивая между собой (6) и (7), находим:

m (2I4I5 — I2 + 2I4I6 — I2 + 2I5I6 — I2)

Ж                4I4I5I6

p11 = p22 = p33 =

^{m (2I}4I5 ^— I 4 ^{+ 2I}4I6 ^— I2 ^{+ 2I}5I6 ^— I6 )

Ж                4I4I5I6

Индексы у давления показывают по каким координатам это давление создается. Рассматривая только пространственные давления (9), нетрудно убедится, что уравнение состояния для плотности энергии и давления имеет вид:

p = —ec2,

(Ю)

что соответствует уравнению состояния вакуума, как формы энергии с постоянной плотностью, независимо от системы отсчета. Следовательно, постулируя существование дополнительных степеней свободы у твердого тела, и повышая тем самым размерность пространства, мы получаем ненулевую энергию, равномерно заполняющую пространство и по своим свойствам сопоставимую с темной энергией.

Рассчитаем, какую часть составляет полученная энергия пустого пространства от критической массы Вселенной. Из формулы (8), подставляя гравитационную постоянную ж = 8C4G, находим, что плотность энергии найдется как:

(2I 4 I 5 - I² + 2I 4 I 6 - I 2 + 2I 5 I 6 - I²)^mc² 20Gnl 4 l 5 l 6

(П)

По определению инерционный радиус несимметричного вращающегося тела, равен:

Rin

________________ 3I 4 I 5 I 6 __________

^m(2I 4 I 5 - Ц + ²I 4 I 6 - I 2 + 2I 5 I 6

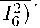
Используя определение инерционного радиуса выразим его из формулы (11):

Rin = V.                                     (12)

2'08 \ Gn

В работе [12] показано, что экспериментально рассчитанная плотность энергии вакуума составляет е_д = (7 ± 1) • 10^-30г см³, тогда, расчет по формуле (12) даст значение равное R in = 20 млрд. св. лет.

Данное теоретически полученное значение по порядку величины совпадает с величиной полученной в работах Нейла. Корниша, который провел детальный анализ топких колебаний в космическом микроволновом фоне, и определил, что верхняя граница, для радиуса Вселенной [13] составляет около 78 миллиардов световых лет.

На. сегодняшний день единственно доступный способ обнаружения гравитации - это наблюдения за движением пробных тел. Поэтому говорить о наличии или отсутствии гравитации можно только с позиции поведения пробного тела. В случае исследования эволюции Вселенной в качестве такого пробного тела, выступает сама. Вселенная, поэтому не удивительно, что радиус инерции равняется радиусу самой Вселенной.

Известно, что критическая плотность энергии может быть найдена по формуле [14]:

_ 3H^{2 Е к} = sGn'

Найдем отношение плотностей энергии Ед и критической плотности Ек'.

Пд =   .

εk

После подстановки (11) и (13) в (14) получаем:

⁽²I 4 I 5 ^— I 2 ⁺ 2I 4 I 6 ^— I^{2 + 2}I5I 6 ^— Г 6) ^{2 т} С 2 Пх = -----------------------------------

^Д                   15H 2 l 4 l 5 l 6

Расчет Пд по формуле (15) с использованием найденного радиуса. Вселенной R in позволяет получить значение:

Пд = 75%.                                        (1G)

Измерения реликтового излучения Вселенной, проведенные спутником WMAP, показывают, что форма Вселенной очень близка к плоской. Но одной только видимой и темной материи не хватает для создания плоской Вселенной, недостающее количество энергии около 70% должна давать темная энергия [1], [12]. Однако недостающие значение энергии может быть получено, как показывают расчеты (16), посредством введения дополнительных степеней свободы тела, и использования семимериого пространства-времени.

С другой стороны, анализируя уравнения поля, записанные в форме (3):

Rmn  5 gmnR  ^Tmn+Amn , можно обнаружить, что они могут быть легко преобразованы к виду:

1     _    3

R mn 2 ^g mn ^{R +} 10 g mn R ^ Tmn + Amn .

И если ввести в обозначение некоторую функцию:

- ,      3

Л(R) = 10 R, то легко получить традиционное гравитационное уравнение поля:

R mn 2 g mn ^R ^ Tmn + Amn

^д тп ^Л(^) ,

с Л космологической постоянной, которую в дальнейшем будем называть динамической космологической постоянной. Ввиду зависимости скаляра кривизны R от масштабного фактора a(t) в метрике Фридмана легко увидеть, что динамическая космологическая постоянная Л также будет зависима от масштабного фактора a(t). Это будет оказывать влияние на эволюцию Вселенной. В работе [15] показано, что наличие переменного Л - члена влияет на процесс эволюции масштабного фактора а на ранней стадии расширения.

Расмотрим метрику расширяющейся Вселенной:

дав    a (t^gae, где индексы а, в = 1-б. Компоненты тензор Риччи для метрики (19) равны:

R 0 =

ба"

c2a,

12 а"   30( а' ) ²   m / I 4     I 5     I 6     111

Eh    с² а^{2  +} О² ( 2I 5 I 6 ⁺ 2I 4 I 6 ⁺ 2I 4 I 5 — I 4 — I 5 — I 6

где штрих означает дифференцирование по времени. Компоненты статической космологической постоянной равны:

_А 0 = - ^m ( I 4 ⁰      5 а² V2 I 5 I 6

+ _А_ + _А_

21 4 I 6    21 4 I 5

--

I 4    I 5     I 6

Для описания барионной материи, заполняющей Вселенную, будем использовать тензор энергии-импульса пыли:

mm

-Г-n — EU U n .

В синхронных координатах материя находится в состоянии покоя, поэтому единственная не нулевая компонента 7-скорости равна: и⁰ = с. Подставляя найденные компоненты тензоров (20), (21), (22) и (23) в уравнение (3), получаем:

18 а" б( а' ) ² 5 с² а ⁺ 5 с² а²

2 = ЖЕС 2 .

Опираясь на уравнение состояния p = ye можно найти зависимость между плотностью энергии е и масштабом Вселенной a(t):

- = -3(1+ y) — .                             (25)

εa

Интегрируя зависимость (25) для барионной материи, находим:

Рис. 1. Изменение масштаба Вселенной со временем

где C - некоторая постоянная. Подставим (26) и ж = 8nG в уравнение (24) и произведем упрощение. Полученное дифференциальное уравнение второго порядка примет вид:

„ _ 15(a^z)² _- 20nGC

9a        9a2

Применяя метод Рунге—Кутты, для решения дифференциального уравнения (27), получаем, что в узком диапазоне граничных условий и значений C эволюция масштабного фактора со временем протекает согласно зависимости рис. 1. Из графика изображенного на рис. 1 видно, что после замедленного расширения, согласно сценарию Фридмана, Вселенная переходит к ускоренному расширению, которое подтверждается наблюдательными данными в настоящее время.

Итоги работы

• 1)    В рамках модели семимерного пространства-времени показана необходимость включения в гравитационные уравнения двух видов космологических констант: статической Amn и динамической A(R).

• 2)    Расчитан инерционный радиус Вселенной, совпадающий по порядку величины с размерами Вселенной.

• 3)    Наличие в гравитационных уравнениях статической A mn и динамической K(R) космологических постоянных оказывает влияние на эволюцию Вселенной, обеспечивая плавный переход от стадии расширения Фридмана к стадии ускоренного расширения.