Динамическая модель гравитационного течения сыпучей зерновой смеси по наклонной поверхности

Гравитационные течения зернистых материалов возникают под действием силы тяжести на склонах, наклонных поверхностях и широко распространены как в природных явлениях, так и в различных технологических процессах. Если при этом угол наклона поверхности близок к углу сухого трения или немного превосходит его, то перемещение частиц по отношению к соседним по высоте слоя является сдвиговым.

Различают три режима гравитационного течения зернистых сыпучих сред: связный, переходный и несвязный. Связный режим характеризуется наличием устойчивых связей между частицами среды – это характерно для процесса прессования порошков, движения сыпучей среды в бункерах и т.д. Несвязный режим сопровождается кратковременными контактами частиц, быстрым нарушением связей между ними и интенсивным перемешиванием относительно друг друга [1]. Граница между этими режимами определяется углом внутреннего трения сыпучей среды.

При угле наклона поверхности близком или чуть превышающем угол внутреннего трения, в сыпучей среде проявляется явление «ожижения», приводящее к разделению сыпучей массы на фракции по толщине слоя, когда в нижние слои уходят наиболее крупные частицы, в верхние – мелкие.

Этот эффект можно использовать для сепарирования зерновой массы на простейших устройствах в виде наклонных желобов с минимальными затратами энергии.

Объект и цель исследования

Несвязный установившийся режим соответствует быстрому гравитационному течению сыпучей среды, которое существует при углах ската близких углу естественного откоса материала. Параметры гравитационного течения зависят от угла наклона ската, и при этом выделяются три вида течения:

• а)    неразвитое скользящее;

• б)    скользящее;

• в)    расплескивающееся.

Вид течения а) наблюдается при углах наклона ската несколько меньших или близких к углу естественного откоса материала. Скорости частиц вблизи основания слоя малы по величине, а профиль скорости по высоте слоя имеет вогнутую форму.

Течение вида б) появляется при небольшом увеличении угла наклона ската относительно угла покоя сыпучей среды. Происходит увеличение скорости частиц, все частицы находятся в движении, и профиль скорости имеет трапециевидную форму.

Вид течения в) появляется при дальнейшем увеличении наклона и сопровождается увеличением скорости сдвига около основания потока сравнительно с его поверхностью. Профиль скорости частиц по глубине слоя становится более гладким, а движение самих частиц характеризуется активным выбросом отдельных частиц на поверхность слоя, которые образуют «облако» частиц несколько меньшей плотности, чем в основном потоке. Взаимодействие верхнего «облака» с воздухом приводит к его торможению и загибу профиля скорости против потока. Во всех трех случаях такие эффекты наблюдаются при достаточно большой высоте слоя.

Цель исследования ‒ изучение процесса самосортирования частиц зерновой смеси в слое зернового материала при движении его в прямолинейном желобе. Новизна состоит в том, что аналитические методы исследования таких течений далеки от завершения и до настоящего момента не создано достаточно адекватных математических моделей.

Механизм разделения зерновой смеси на фракции, отличающиеся по различным физическим свойствам, зависит от многих факторов. Устройство, реализующее рассматриваемый эффект разделения смеси на фракции, представлено на рисунке 1.

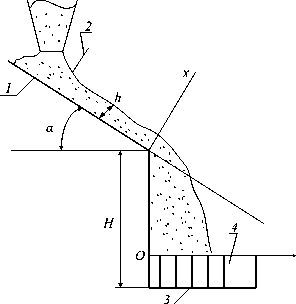
Рис. 1. Установка, производящая разделение сыпучей смеси на фракции

Установка имеет следующие элементы конструкции: 1 – наклонная рабочая поверхность; 2 – затвор для регулирования высоты потока смеси; 3 – приемник с разделительными стенками; 4 – ячейки приемника.

Регулировочные параметры: α – угол наклона скатной поверхности; h – толщина потока смеси; Н – высота полета частиц до решетчатого приемника; х – текущая координата по высоте слоя.

Установка работает следующим образом. Поток сыпучей среды по толщине формируется заслонкой 2 и движется вниз по наклонной поверхности 1. В процессе движения легкие и мелкие частицы «всплывают» вверх и с разными скоростями разные фракции попадают в различные ячейки приемника 4, самые крупные фракции попадают в ближние ячейки, а легкие фракции – в дальние. Таким образом происходит сепарирование сыпучей смеси на фракции.

Результаты исследования

Математическая модель этого процесса строится на следующем допущении. Весь процесс разделения смеси на фракции определяется поверхностными силами взаимодействия при соударениях частиц и объемными силами, зависящими от объема самих частиц. Таким образом, представляется возможным взять за основу математической модели соотношение между поверхностными и объемными силами, действующими на отдельную частицу сыпучей смеси.

В работе [1] приводятся результаты экспериментально-аналитического исследования в виде профиля скорости u(x), порозности (концентрации твердой фазы) e (x), где х – координата по высоте слоя (рис. 2).

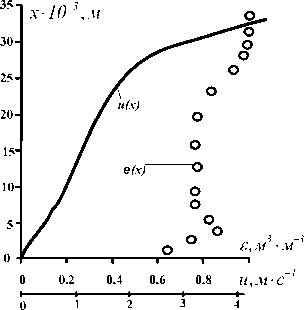
Рис. 2. Профили скорости и порозности гранул диаметром 6,6∙10-3 м

Следуя выводам этих исследований, вся зерновая масса представляется состоящей из частиц эллипсоидной формы (рис. 3), а, b, c – полуоси эллипсоида.

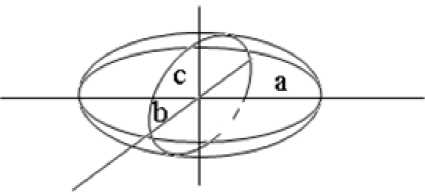
Рис. 3. Приближенная форма зерновой частицы – эллипсоид

В первом приближении для зерновой частицы характерно следующее соотношение между размерами по осям симметрии:

a

Объем и площадь поверхности эллипсоида выражаются следующими формулами:

4 к na .

• V = п • abc =      ;

S = 4 п

( a^pd^p + b^pc^p + c^pa^p ) 1 р

где p « 1,6 .

С учетом условия (1) формулы (2), (3) преобразуются в следующий вид:

V = 1,04a³, S = 0 , 5 • a ² .                                     (4)

Далее введем величину отношения объема к площади эллипсоида

D ( a ) =

V ( a ) S ( a )

1,04 a ³

0,5 а ²

» 2 a .

Далее примем а ≈ а с р – средний размер зерновой частицы по большой полуоси. Зададимся следующими геометрическими размерами частиц зерновой смеси: a mn = 0,004 м, a m = 0,006 м , а ср = 0,005 м .

Тогда величина

D ( a ) = 2 a_cp = 2 • 0,005 = 0,01 м .

Таким образом, при движении сыпучей среды по наклонной плоскости под действием силы тяжести в ней проявляются свойства жидкости и появляется действие архимедовой силы, вследствие чего происходит разделение неоднородной среды на фракции. Этот процесс адекватно зависит от параметра D(a) и может быть описан уравнением обратной диф- фузии [2]:

д a (x t) д t

= - d ( a) ^^ д x

где a (x, t) ‒ функция размера частицы по высоте потока х, времени t, отражающая распределение зерновых частиц внутри сыпучей среды.

Решение уравнения (6) будем искать методом разделения переменных. Представим решение уравнения (6) в следующем виде:

a (x, t) = X(x) • T(t).                                            (7)

Подставив (6) в (5), получим: X(x) - T'(t) = -D( a )X"(x) - T(t ).

Далее разделим переменные

TKt) = -D( a )XM = - X 2 .

T(t)         X(x)

Здесь - X <  0 при любых X, так как решение уравнения (6) должно иметь экспоненциальную форму.

Выражение (8) разделим на два обыкновенных дифференциальных уравнения, где корни характеристических уравнений действительные.

T'(t)- X T(t) = 0

^< X''(x)- ^{X X(x)} = 0

[         D( a )

.

Интегрируем (9) известными методами

а)

T^ = -X , lnT(t) = - X t + In C, ,

T(t)        ^{,                          1}

ln^T(t) = - X t , TW = e"X t , C 1        ^,   C 1

T(t) = C,e ^{- X t} .

б) второму уравнению соответствует характеристическое уравнение с действительными корнями

k2

-

k1,2

^X = 0

D( a )     ,

= ± ^X^2 a_cp = ±7 X 12 - 0,005 = ±xj 0,01 = ± 0,1 2 .

Соответственно общее решение имеет вид

X(x) = C₂ e ^k ' ^x + C e k^{2 x} = C₂ e

Решение уравнения (6) приобретает следующий вид

-(

-0 , 1 X x ₊ q ^0 , 1 X x

.

a (x, t) = Ce ^{- X t} (C₂ e

-(

■ 0 , 1X x  . x-r 0 , 1X xx

+ C 3 e ⁾

.

Неизвестные величины С 1 , С 2 , С 3 , λ найдем из начальных и граничных условий.

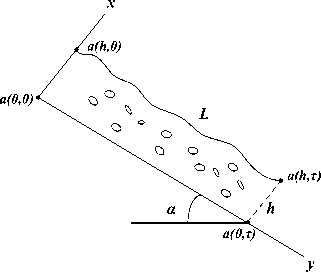
Рис. 4. Схема распределения функции a (x,t) по точкам потока зерновой смеси

На схеме τ – время наблюдения за процессом; L – длина желоба; h – толщина смеси в желобе.

a ( 0 - 0 ) = а ср

.   а (0- ") = аср a (Т0 ,0) = a max

_ a ' ⁽ T _h , h ) = a min .

Таким образом, приходим к системе нелинейных уравнений:

Г С , ( C 2 + C 3 ) = а_Т

• С , ( С 2 e - 0 - 1 ^ " + С з e ⁰ - 1 ^ " ) = а ср 'с Ле ^{- х2т} 0 ( С 2 + С з ) = a max _ С,е ^{- Лт} " ( С₂ e ^{- 0 - 1 Л} " + С₃ e ^{Л 0 -} 1" ) = а _ш„■

LL

Т =    - Т =    -

• ^{0    V}0     ^{h    V}h

  
  
  
  

где V 0 – скорость частиц на поверхности ската; V h – скорость частиц на поверхности потока.

В системе Matchcad построим графическую интерпретацию математической модели распределения зерновых частиц сыпучей среды по толщине слоя с течением времени. На графиках (рис. 5, 6) показано влияние архимедовой силы на разделение неоднородной сыпучей среды на фракции.

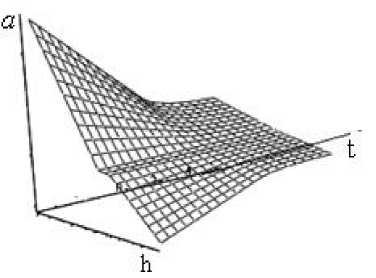
Рис. 5. Графическая интерпретация модели распределения зерновой смеси по высоте с течением времени

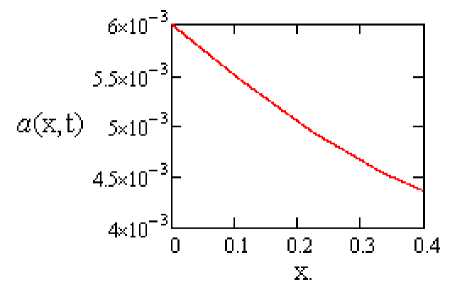
Рис. 6. Распределение зерновой смеси по высоте потока в момент времени t=5 с

Выводы