Динамическая модель контактирования при фреттинге бандажных полок лопаток компрессора низкого давления газотурбинного двигателя

Проблема повышения фреттингостойкости деталей малоподвижных и номинально неподвижных соединений, работающих в условиях вибраций и повторно-переменных нагрузок, является одной из наиболее важных. Износы при фреттинге бандажных полок титановых лопаток компрессора низкого давления ГТД приводят к снижению натяга по окружности бандажа, механического демпфирования в системе, вибрационной прочности лопаток, разрушению поверхностей замковой части, к потере других эффектов бандажирования [1].

Фреттинг-процессом занимались отечественные и зарубежные исследователи [2] однако единых представлений о природе фреттинг-износа и мерах по его предупреждению не достигнуто. Недостаточно систематических исследований по оценке механических параметров контактирования с учетом реологии фреттинг-износа титановых сплавов.

Целью работы является разработка динамической модели контактирования бандажных полок лопаток ГТД и её математическое описание, с учетом упругих и диссипативных свойств материала лопаток и изнашиваемого стыка полок, для расчета параметров контактного взаимодействия (амплитуды относительных перемещений, частоты колебаний, нагрузки в стыке) в условиях многокомпонентной вибрации, необходимых для моделирования и проведения испытаний, расчета износа и прогнозирования фреттингостойкости.

СХЕМА КОНТАКТИРОВАНИЯ ЛОПАТОК

Рассматривается, с учетом общепринятых допущений [3], схема контактирования соседних лопаток осевого турбокомпрессора ГТД под действием переменных газовых сил в системе координат X, Y, r (рис.1). Оси X, Y, r связаны с вращающимся диском и проходит через центры тяжести корневых сечений лопаток (О₁, О₂). Ось Y направлена по потоку газов вдоль оси вращения турбины, ось X – в плоскости вращения, ось r – вдоль радиуса диска. Считается, что выносы центров тяжести поперечных сечений лопатки от оси r небольшие, поэтому направление оси r принимается вдоль оси лопатки, совпадающим с осью Z, поперечные сечения лопатки перпендикулярны оси Z, а оси X₁, X₂ и Y₁, Y₂, проходящие через центры тяжести сечений полок, параллельны, соответственно, осям X, Y. Оси ξ ₁, ξ ₂ и η ₁, η ₂ – главные центральные оси сечений, при этом ξ _i – ось наименьшей жесткости, ∆ φ ₀ – угол между осями соседних лопаток в диске.

Переменные газовые силы, приведенные к центрам тяжести Ц1 и Ц2 сечений полок можно представить [3] в виде:

P_r(t)=P_cp+P₁sin(2πnt+ φ ₀₁)+...+P_ksin(2π(kn)t+ φ _0k), (1) где P cp –^cp среднее значение газовых сил на заданном режиме; P₁,..., P_k– амплитуды сил соответствующих гармоник, φ ₀₁,..., φ _0k – их фазы; n – частота вращения ротора.

Раскладывая, в соответствии с правилами механики , вектор газовых сил Pr1(t) на составляющие по осям X1, Y1 и перенося их в точку О1 центра тяжести корневого сечения лопатки видим, что полка совершает колебательные перемещения совместно с лопаткой вдоль осей X, Y, Z (см. рис.1) под действием динамических со-

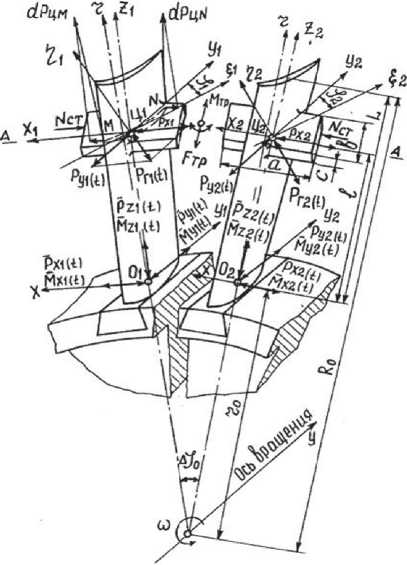
Рис. 1. Схема контактирования лопаток компрессора ставляющих газовых сил Px1(t), Py1(t) и динамической центробежной силы Pz1(t), а также крутильные колебания вокруг оси Z1 под действием динамического момента Mz1(t) от пары сил dPцМ и dPцN. Лопатка, кроме того, совершает крутильные колебания вокруг осей X и Y под действием динамических моментов Mx1(t), My1(t) (на рис.1 показаны векторы этих моментов направленные перпендикулярно плоскостям действия пар сил). Аналогичны динамические схемы контактирования остальных пар лопаток колеса компрессора. Из приведенного анализа следует, что особенностью рабочего режима контактирования в замках и по бандажным полкам лопаток турбокомпрессора в поле действия периодически изменяющихся газовых сил является наличие относительных тангенциальных, нормальных и крутильных колебаний по всем шести степеням свободы, вызывающих интенсивный фреттинг-износ поверхностей.

ДИНАМИЧЕСКАЯ И РАСЧЕТНАЯ МОДЕЛИ КОНТАКТНОЙ ПАРЫ

На основе проведенного выше анализа с использованием традиционных приемов схематизации и допущений [3, 5] динамическая модель (рис.2) представлена двухмассовой системой с шестью степенями свободы. Массы М1 и М2 равны между собой и являются приведенными сосредоточенными массами контактирующих лопаток. Массы имеют упругие и диссипатив-

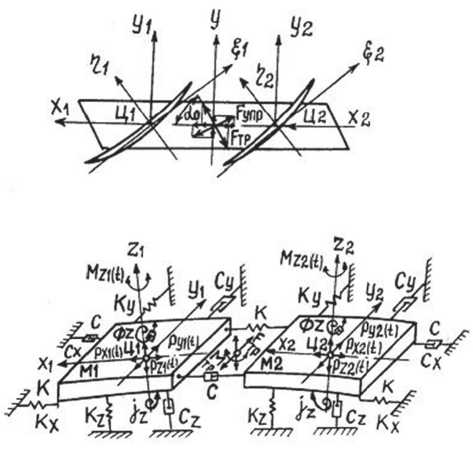
Рис. 2. Динамическая модель контактирования бандажных полок ные связи в направлении действия компонент возмущающих сил и моментов. Упругие Kx, Ky, Kz, jz и диссипативные Cx, Cy, Cz, Фz связи полок с жестким телом лопаток имеют линейные характеристики. Упругие K и диссипативные С связи изнашиваемого стыка полок нелинейны. Эти характеристики подвергались специальному экспериментальному исследованию, результаты которого и установленная нелинейность связей учтены при их математическом описании.

Процедура контактного взаимодействия состоит в том, что за один период колебаний нормальная составляющая возбуждающих сил Pxi(t) (см. рис.2) вызовет контактное сближение поверхностей полок. При этом произойдет рассеяние упругой энергии импульса на деформирование материала в шероховатом контакте и в нижележащих слоях металла. Одновременно с процессом сближения происходит контактное трение под действием возмущающих сил Pyi(t), Pzi(t) и моментов Mzi(t), Mxi(t), Myi(t). Предварительный количественный анализ модели показал, что наибольший вклад в контактные вибросмещения полок вносят изгибные колебания лопаток [4] в направлениях ЦiXi и ЦiYi, в плоскости их наименьшей жесткости ηiЦiZi (рис.1), и крутильные колебания относительно осей ЦiZi. Поэтому, наряду с традиционными, сделаны следующие допущения: поступательные степени свободы полок в направлении осей ЦiZi и вращательные вокруг осей ЦiXi и ЦiYi не учитываются вследствие повышенных (на два, три порядка) модулей жесткости растяжения-сжатия и изгиба стержня лопатки; бандажную кольцевую связь, с которой взаимодействует выделенная элементарная ячейка колеса компрессора (см. рис. 2), принимаем абсолютно жесткой; колебаниями вала и диска компрессора пренебрегаем, что мотивируется их значительным начальным нагружением.

Рассмотрим движение двух точек, принадлежащих сосредоточенным приведенным массам М1 и М2 полок, в трехмерном пространстве с центрами координат Ц1 и Ц2. С учетом схемы действия сил и связей (рис. 2), а также принятых упрощений система уравнений движения деталей контактной пары примет вид:

M X -FMlX )- F„ ^(,) (X , )- F tx (X i )- F_tx(X , -X₂). F cx (X i )- F cx (X i - X 2 )- F^X i )-^ -F_lx(X , -X₂)+P_xl(t),

MX .— l_k ; ^l ^X . )- F_C x ^|2) ( X 2 )- F tx (X 2 )- F tx (X 2 - X , )- F_C x (X 2 )- F_C x (X 2 - X , )- F tx (X 2 )-

^-F tx ^(X 2 ^{- X} l ^)+P x2 ^(t),                                                                            / О \

MF -hxX Y )- Ь/^ ) - F t, (Y , )- F t, (Y , - Y 2 )- F t _y(F i )-F t _y(Y i - X₂)+P yi (t),     ( (2)

MY 2 =-F t _y ^,2, (Y 2 )- F_C y> ²⁾ ( F 2 )- F ty (Y 2 )- F ty (Y 2 - Y i )-F ty (Y 2 )-F ty (F 2 - X i )+P y2 (t),

I Ф —Mz^x i-MJXyj )-M_/У2 )-M , (0 -оз-Мм^ )-Мм ф -ф j-M , ш, 1 2 ^ 2 =-М_ух ⁽²⁾ (ф 2 )-М ф _х ’ ²⁾ ( ^ 2 )-М_ух(ф 2 )- M_jz(ф 2 -ф l )-M_lz(p 2 )- M , _z(^₂-^₁)+M₂₂(t),

Опишем каждую составляющую системы уравнений (2) движения полок.

М=М1=М2 – приведенная масса полки.

i=d2Xi/dt2, i=d2Yi/dt2 , где Xi Yi – линейные перемещения полок вдоль соответствующих координатных осей.

I_i – приведенные моменты инерции полок относительно осей Ц_iZ_i. _i=d² φ _i/dt² , где φ _i – угловые перемещения полок относительно осей Ц_iZ_i.

Линейные упругие силы лопаток в направлениях X и Y

F⁽ⁱ⁾ кx (X i )=K x X j =3EJ y X i /l³ ,

F(i)ky(Yi)=KyYl=3EJxYi/l3 , (3) где Е – модуль упругости материала лопатки; Jx, Jy – осевые моменты инерции сечения лопатки; l – длина лопатки от корня до центра масс полки (рис. 1).

Линейные моменты сил упругого сопротивления относительно оси Z, обусловленные крутильной жесткостью jz лопаток

M⁽ⁱ⁾_jz( φ _i)=j_z φ _i≈0.38EJ_p φ _i/l , (4) где J_p – полярный момент инерции сечения лопатки.

Линейные силы демпфирования лопаток в направлениях Х и Y

F⁽ⁱ⁾ ( )=C =2M δ f , cx i x i m x i ,

F⁽ⁱ⁾ cy ( i )=C y i =2M δ m f y i ,

где δ _m– логарифмический декремент колебаний материала лопаток; f_x, f_y – частота колебаний в направлении координатных осей Х и Y, определяемая с учетом свойств материала, конструктивных особенностей и форм колебаний лопаток в поле центробежных сил [3].

Линейные моменты сил демпфирования лопаток относительно оси Z

M⁽ⁱ⁾ фz ( i )=Ф z i =2J i δ м f мz i ,              (6)

где fмz – частота крутильных колебаний лопатки [3].

Возмущающие силы и моменты:

Pxi(t)= Pxi i sin2tot+Px2isin4tot+Px3isin6tot,

P x2 x i2 sin(2mt+^ o )+P_X 22 sin(4mt+^ o )+P_X 32 sin(6mt+^ o ),

P_yi (t)= P_{yi i} sin2tot+P_y2isin4tot+P_y 3 ₁ sin6tot,

P y2 (t)= P yi2 Sin(2tot+^ o )+P y22 Sin(4tot+^ o )+P y32 Sin(6tot+^ o ),

M_z i (t)= M zii sinrot,

M z2 zi2 sin(tot+^ o ) ,

где φ ₀=2π/Z – фазовое положение полки (лопатки) на периферии диска, Z – число лопаток.

Возмущающие силы и моменты представляются в виде периодических функций, раскладываемых в ряд Фурье. При этом, как показала практика, достаточно ограничиться тремя основными гармониками, так как не учитываемый спектр возмущений меньше точности решения дифференциальных уравнений (2). Амплитуды возмущающих сил определяются по спектрограммам напряжений в лопатках [3] путем статистического прогнозирования. Практика показала, что переменные напряжения у корня лопаток вдали от резонансов не превышает 2-4% от средних постоянных. В плоскости бандажных полок уровень переменных напряжений может достигать 10% и более [1], в связи с чем амплитуды возмущающих сил следует варьировать в пределах 2-20% от средних постоянных.

Нелинейные упругие силы в изнашиваемом стыке:

F_K x (X i )=K(X o +X i ),         )

F_K x (X i -X 2 )= K(X o +X i - X 2 ),

F kx (X 2 -X i )= K(X o +X 2 -X i ), I F Ky (Y i )=K(Y o +Y i ),

F Ky (Y i -Y 2 )= K(Y o +Y i - Y 2 ),

FKy(Y2-Yi)= K(Yo+Y2-Yi), J где X0, Y0 – сближение в контакте обусловленное предварительным натягом на полках, создаваемом при сборке лопаток в колесо.

Нелинейные моменты упругих сил относительно оси ЦiZi:

M_jz (p i )=o,5[F _kx (X i ,_V i )b+F _ky (¥ i ,_V i )a],

M_J z (_V i -_V 2 )=o,5[F _kx (X i -X 2 )b+F _ky (¥ i -Y 2 )a], ^ (9)

MJz(ф2-фl)=0,5[Fkx(X2-Xl)b+Fky(¥2-¥l)a],J где a и b – длина и ширина полки (рис. 1).

Нелинейные силы демпфирования в стыке:

F_cx(X_l)CX_l 2M6i x _iX„

F ex (¥ i -¥ 2 )=2M5f x (¥ i -¥ 2 ), *

F cx (W i )=2M5f x (M i ),

где δ – логарифмический декремент колебаний в изнашиваемом стыке, fx – частота колебаний в стыке в направлении X, fx= K / M /(2π).

Силы и моменты сил трения:

F tx ^—F kx Ц^cO^sU o ^, F t_y =F kx Цsina o, >

M t_z =G,5-a- F t_y ,

где μ – коэффициент трения в стыке полок, α ₀ – угол наклона стыка полок к оси ЦX (рис. 1).

Представление разработанной динамической модели контактной пары, специфика которой раскрыта уравнениями (1-12), как суперпозицию возмущающих сил и нелинейной реакции системы на эти воздействия делает ее универсальной, применимой к расчету нормальных и касательных виброперемещений в номинально неподвижных и малоподвижных плоских стыках широкого круга соединений в машинных.

Нелинейные контактные характеристики изнашиваемого при фреттинге стыка: контактная жесткость К, диссипативность С (логарифмический декремент колебаний в стыке δ ), коэффициент трения μ и их зависимости от параметров внешних воздействий оценивались экспериментально на лабораторных образцах.

Результирующей проверкой адекватности параметров разработанной модели по отношению к объекту явился численный эксперимент, подтвердивший количественно правомерность принятой схематизации и несущественную роль приведенных выше упрощений.

РЕШЕНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ ДЕТАЛЕЙ КОНТАКТНОЙ ПАРЫ

Экспериментальная зависимость контактного давления от сближения получена в виде:

q=cm∆sn, (13)

где q – давление в стыке в Н/м2; ∆ – нормальное сближение в м; m=1,85, sn=1,3 – средние значения эмпирических коэффициентов, аппроксимирующих нелинейную зависимость контактного давления от сближения; с=1013,8 - коэффициент приведения размерностей в систему СИ.

Полагая q=Fк/S, где S – номинальная площадь контакта, получим выражение для упругой силы

где Mk=q/q0 – коэффициент, учитывающий ослабление предварительного натяга q0, создаваемого в контакте при сборке лопаток в колесо, в результате износа торцов бандажных полок. Применение коэффициента Mk вызвано тем, что, натяг по полкам ослабевает уже в первые часы работы колеса [6], а при наработке 900-1500ча-сов натяг исчезает и между контактными поверхностями полок появляется зазор.

Для удобства программирования поделим правые части уравнений (2) на множители перед второй производной перемещений и введем новые обозначения. Тогда, нелинейные упругие силы изнашиваемого стыка (8), отнесенные к приведенной массе полки, запишутся в виде:

FК1(X)= Fкx/M=K(X)(X0+X);

FК2(X,Y)=Fкy/M=0,4K(Х)(Y0+Y), (15)

где K(X)=(cmMk/M)S(X0+X)sn-1 – отнесенный к приведенной массе полки коэффициент нормальной жесткости, зависящий от сближения в контакте X(∆); 0,4 – коэффициент приведения к тангенциальной жесткости в контакте [5];

X_o=A_osina_o=^sryq o /cm-sina_o ; Y_o~^sryq o /cm-cosa_o ,

где ∆0 – нормальное сближение в контакте при давлении предварительного натяга q0.

Приведенная масса полки

M=M1=M2=Mп+(lz/l)MЛ ,        (17)

где Mп – масса полки, MЛ – масса лопатки (без учета массы замковой части), lz – расстояние от корня до центра масс лопатки.

Линейные упругие силы пера лопатки в направлении Y (3) преобразуются к виду:

FК3(Y)=3EJxY/(Ml3),           (18)

а силы демпфирования в стыке (10), с учетом (11), к виду

FC(X, X )=5 X V К ( X ) л.        (19)

Трение в контакте (12) представим функцией FT(X, Y )=sign Y -FK1(X) • (Ь з +Ь 1 ехр(Ь₂| У |)), (20)

где sign – функция, учитывающая изменение направления силы трения в контакте при изменении направления векторы скорости относительного проскальзывания; b3+b1exp(b2| |)=μ-экспериментально полученное выражение коэффициента трения в стыке, где b1=0,5, b2=-500, b3=0,53 - эмпирические коэффициенты.

Момент упругих сил (9), возникающий в контакте при закручивании зажатой (рис.1) с обеих сторон полки

M_j=(b²/12)K(X) ^. φ . (21)

Поделив (21) на R=a/2, где R – радиус про- скальзывания на полке, получим

FM(X, φ )= (b²/12R)K(X) ^. φ .        (22)

В уравнениях (7) ограничимся первым членом разложения в ряд Фурье и обозначим функции

FB1=sin(2πft),

FB2=sin(2πft + φ ₀),            (23)

где f=n/60 – частота колебаний в ГЦ.

В условиях нераскрытия стыка полок (при коэффициенте ослабления натяга Mk≥0,1) силами и моментами упругости и демпфирования стержней лопаток можно пренебречь, вслед- ствие их малости (на два, три порядка) по срав- нению с силой трения в контакте. Тогда, в принятых обозначениях (13-23), система уравнений движения (2) перепишется в виде:

X1=FK1(-X1)-FK1(X1-X2)-FC(-X1,X1)-FC(X1-X2,X1-X2)+(Px11/M)FB1;      '

X ₂=FK1(X₁-X₂)-FK1(X₂)-FC(X₂, X₂)-FC(X₁-X₂, X₂-X₁)+(P_x12/M)FB2;

P 1 =-FK2(-X 1 , Y 1 )-FK3(Y 1 )-FK2(X 1 -X 2 , Y 1 -Y 2 )-FT(-X_b Г 1 )-

-FT(X 1 -X 2 , K 1 -K 2 ))+(P y11 /M)FB1;

p 2 =-FK2(X 2 , Y 2 )-FK3(Y 2 )-FK2(X 1 -X 2 , Y 2 -Y 1 )-FT(X 2 , Г 2 )-

• -FT(X₁-X₂, Г ₂- Г ₁) )+(P_y12/M)FB2;

^ ₁=(MR/I₁)(-FM(-X₁ ,ф₁ )-FM(X₁ -x₂,ф₁ -v₂)+FK2(-X₁ , Y₁ )-FK2(X₁ -X₂, Y₁ -Y₂)-

• -FT(.X 1 , y 1 )-FT(X 1 -X 2 , ? 1 -? 2 ))+(M_z 11 /I 1 )FB1;

^ 2 =(MR/I 1 )(-FM(X 2 ,V 2 )-FM(X 1 -X 2 ,V 2 -V 1 )-FK2(X 2 , Y 2 )+ FK2(X 1 -X 2 , Y 2 -Y 1 )-

-FT(X 2 , y 2 )+FT(X 1 -X 2 , / 2 -^ 1 ))+(M_z 12 /I 1 )FB2;                                  ,

где

I 1 =J_vp²dV=jjj(X²+Y²)dzdydx=(M/12)(a²+b²). (25)

Введем обозначения:

Z(1)=X₁; Z(2)=X₂; Z(3)=Y₁; Z(4)=Y₂; Z(5)= φ ₁;

Z(6)= φ ₂; Z(7)= ₁; Z(8)=  ₂; Z(9)= ₁; Z(10)= ₂;

Z(11)= 1; Z(12)= 2 .

Система (24) примет вид:

DZ(1)-Z(7);

DZ(7)-FK1(-Z(1))-FK1(Z(1)-Z(2))-FC(-Z(1),Z(7))-FC((Z(1)-Z(2)),

(Z(7)-Z(8)))+(P_X ii /M)FB1

DZ(2)-Z(8);

DZ(8)-FK1(Z(1)-Z(2))-FK1(Z(2))-FC(Z(2), Z(8))-FC((Z(1)-Z(2)),

(Z(8)-Z(7)))+(P_X 12 /M)FB2;

DZ(3)-Z(9);

DZ(9)-FK2(-Z(1),Z(3))-FK3(Z(3))-FK2((Z(1)-Z(2)),(Z(3)-Z(4)))-FT(-Z(1), Z(9))-FT((Z(1)-Z(2)),(Z(9)-Z(10)))+(Py„/M)FB1;

DZ(4)-Z(10);                                                           , (26)

DZ(10)--FK2(Z(2),Z(4))-FK3(Z)4))-FK2((Z(1)-Z(2)), ((Z(4)-Z(3)))-FT((Z(2), Z(10))-FT((Z(1)-Z(2)),(Z(10)-Z(9))))+(P y12 /M)FB2;

DZ(5)-Z(11);

DZ(11)- (MR/1 1 )(-FM(-Z(1), Z(5))-FM((Z(1)-Z(2)), (Z(5)-Z(6)))+FK2((-Z(1),Z(3))-

-FK2((Z(1)-Z(2)),(Z(3)-Z(4)))-FT(-Z(1),Z(9))-FT((Z(1)-Z(2)),(Z(9)-Z(10))))+(M ,11 /I 1 )FB1;

DZ(6)-Z(12);

Dz(12)-(MR/I 1 )(-FM(Z(2), Z(6))-FM((Z(1)-Z(2)), (Z(6)-Z(5)))-FK2(Z(2), Z(4))+ FK2 ((Z(1)-Z(2)), (Z(4)-Z(3)))-FT(Z(2), Z(10))+FT(Z(1)-Z(2))), (Z(10)-Z(9)))) +(M ,12 /I 1 )FB2.

Система уравнений (26) имеет нормальную форму и входит в техническое задание на про граммирование .

Результаты решения рассмотренных диффе ренциальных уравнений движения бандажных полок лопаток компрессора низкого давления приведены на рис .3 при следующих исходных данных : M=4 ^. 10^-1, X₀=6,25 ^. 10^-6, E=1,1 ^. 10¹¹, I=2 ^. 10^-8, R=4 ^. 10^-2, F=2 ^. 10², I₁=2,37 ^. 10^-4, X_k=2 ^. 10^-1, S=1,68 ^. 10^-4, L=2,4 ^. 10^-1, a=2,4 ^. 10^-2, b=2,8 ^. 10^-2, I₂=2,56 ^. 10^-9, F₁=1,57 . 10^-1, α ₀=90^o.

Численное исследование модели показало, что, в условиях нераскрытия стыка полок, упругие колебания в нормальной плоскости происходят (рис. 3а) в пределах остаточного предва- рительного натяга X0 c амплитудой X=(0,05-0,2) мкм. В тангенциальной плоскости (рис. 3б) амплитуда относительного проскальзывания изменяется в пределах Y=(0,2-0,6) мкм. Наибольшее проскальзывание в контакте возникает при крутильных колебаниях полок (рис. 3в) Lt=∆φ.R= (5-30) мкм, где ∆φ – угол закручивания лопатки.

ЗАКЛЮЧЕНИЕ

Разработанная динамическая модель кон тактирования при фреттинге бандажных по лок лопаток компрессора низкого давления газотурбинного двигателя может быть ис пользована для расчета относительных ви броперемещений в зоне трения полок в на правлении компонент возмущающих сил и моментов в условиях многокомпонентной вибрации лопаток . Возможно также решение задач оптимизации геометрических , кинема тических и динамических параметров кон такта , площади контакта , положения стыка полок в пространстве , предварительного на тяга на полках при сборке лопаток с целью минимизации вибросмещений , оценки вли яния на вибросмещения упрочняющей обра ботки , покрытий , смазок путем оптимизации упругих и диссипативных свойств изнашива емых поверхностей контакта .

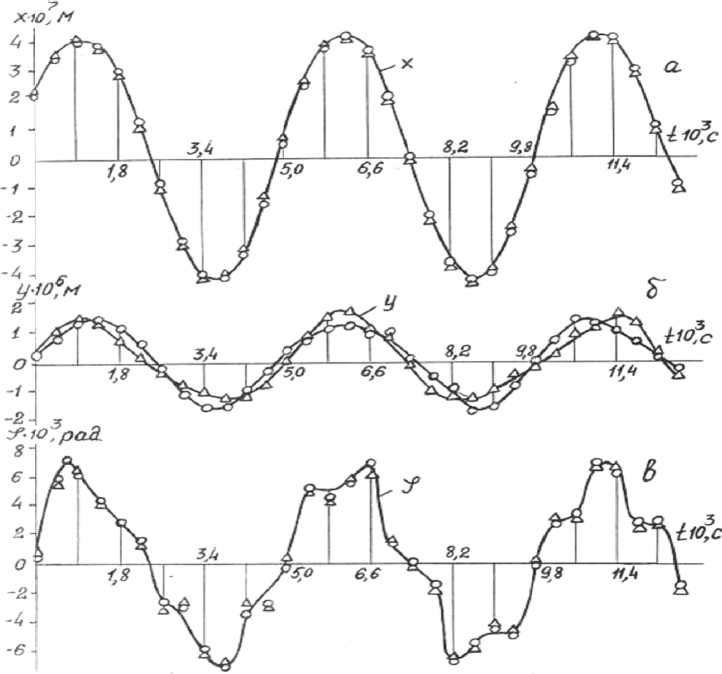
Рис. 3. Микросмещения бандажных полок лопаток :

а – нормальные , б – касательные , в – угловые . o – X₁, Y₁, φ ₁; ∆ – X₂, Y₂, φ ₂