Динамическая модель механизма с параллельной кинематикой

Перспективность использования механизмов с параллельной кинематикой при построении технологического оборудования в силу ряда их положительных качеств не вызывает сомнений [1]. При проектировании технологического оборудования, построенного на основе таких механизмов, возникает потребность в решении задач кинематики и динамики.

Решение задач кинематики позволяет связать между собой при помощи математических зависимостей выходные координаты механизма с его обобщенными координатами: прямая задача связана с определением выходных координат по известным обобщенным; цель решения обратной задачи - определение обобщенных координат по заданным выходным. Составление уравнений кинематики рассмотрено во многих публикациях, например [1, 2]. Эти уравнения могут использоваться при анализе рабочего пространства механизма с параллельной кинематикой [3], а также при решении траекторных задач применительно к технологическому оборудованию, построенному на основе подобных механизмов [4].

Динамический анализ позволяет учитывать такие параметры конструктивных элементом технологического оборудования, как масса и моменты инерции. Прямая задача динамики - определение параметров движения элементов оборудования и возникающих в них усилий при заданных усилиях приводов - представляет интерес при проверочных расчетах и при моделировании функционирования оборудования. Решение обратной задачи динамики - определение усилий приводов, необходимых для обеспечения движения исполнительного органа оборудования в заданном направлении или с заданным усилием - представляет интерес как с позиций управления оборудованием, так и с позиций проектирования: получаемая в ходе решения этой задачи информация о характере движения элементов оборудования (линейных и угловых скоростях и ускорениях) с учетом их массо-инерционных характеристик и возникающих в них усилиях может использоваться в прочностных расчетах.

При решении задач динамики возникает необходимость в получении уравнений, позволяющих описывать поведение оборудования с учетом массо-инерционных характеристик его элементов, т. е. в построении динамической модели. Эти уравнения позволят осуществлять моделирование работы оборудования на качественно более высоком, по сравнению с уравнениями кинематики, уровне, в том числе обеспечивая исследования динамических погрешностей при решении траекторных задач.

Рассмотрим динамическую систему, в которую входят механизм типа «гексапод» [1] и приводы, обеспечивающие движение элементов этого механизма. Гексапод включает в себя подвижную платформу, соединенную с основанием с помощью шести штанг, способных изменять свою длину (рис. 1). Примем, что обобщенными координатами q₍ для этого механизма являются величины, связанные с длинами штанг.

Подвижная р_вн

Штанги

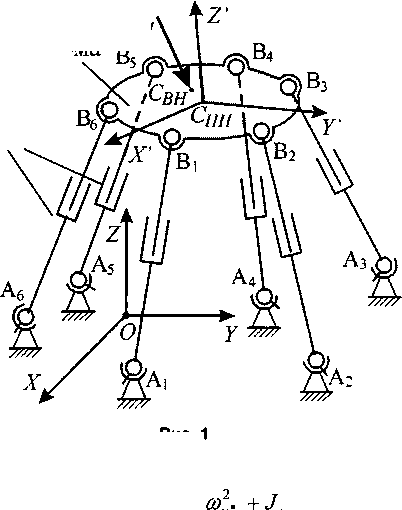
Рис. 1

Для составления уравнений динамики данной динамической системы можно воспользоваться уравнениями Лагранжа 2-го рода [5]:

а\ аг dtyjacp

r=QPj=^,

где Т - кинетическая энергия системы; Qj - обобщенная сила, соответствующая j-й обобщенной координате.

Рассмотрим одну из штанг переменной длины (рис. 2). Штанга состоит из двух частей: нижней массой т_хн и верхней массой т_хв, соединенных посредством поступательной кинематической пары. Определим кинетическую энергию этой штанги.

Нижняя часть штанги может рассматриваться как твердое тело с одной закрепленной точкой А], поэтому ее кинетическая энергия может быть записана в следующем виде [5]:

Т ю ю _j ю ю _J ю ю , (2) 2 мнАн мн Ан Анмн Ан Ан мнмн -ан мн где компоненты тензора инерции нижней части штанги JXH и проекции угловой скорости ®хн записаны для осей связанной со штангой подвижной системы координат A.xXxhYxhZxh . Компоненты тензора инерции при этом будут постоянными величинами. Если оси системы координат XxXxhYxhZxh являются главными осями инерции для нижней части штанги в точке А], то выражение для кинетической энергии примет следующий более простой вид:

т- _ ^Х1Н ^Х\Н Ан Ан ^zw ^z\h

Верхний элемент штанги совершает сложное пространственное движение. Кинетическая энергия этого элемента в соответствии с теоремой Кёнига будет складываться из двух составляющих: кинетической энергии движении центра масс С15 в предположении, что в нем сосредоточена вся масса элемента, и кинетической энергии вращения элемента вокруг центра масс:

гр _ грЦ.М . ’рВр 1\в -^в  ^*\в *

Первое слагаемое в (4) можно записать следующим образом:

^8 М'- 27И18|тС|д| .

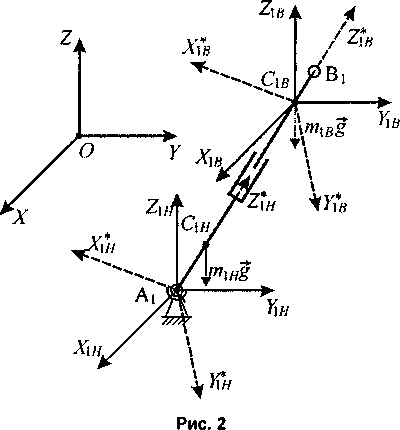
Скорость v_Cifi точки С_хв определяется как

V_C]S =|A]C_ls|S] + ^, следовательно, |т_С]Д|² = [AjC^]² оу,² + ^²

(так как 5] ± ^ ) и

Тхцвм =^тхв

|А]С1Д|2(®2. + <У2. + ®2. ) + £[ , 1 МН цн ^лн где qx - производная по времени обобщенной координаты. В качестве обобщенной координаты можно принять длину штанги - расстояние между шарнирами А] и В,, однако с целью упрощения математических выкладок примем за обобщенную координату длину |A]CW|. Тогда

Tjs ~ 2 ^W1S 9^х ^®.

2           7          2 х • 2

' • +(0". +0 . ) + ^ . ^х\н    чн    Ан

Второе слагаемое в (4) можно записать аналогично (2):

„ JсоЧ *J.co\*J . соЧ

Т^ВР- х_хв Х_хв Y_XB У₁₅ ____ Z_XB Z_XB ,                _ ,               _ ,

• ¹⁸                     2                      -^IS^lS Х_хв Y_XB Y*_BZ_XB Y_XB Z_XB Z_XBX_XB Z_XB X_XB ’

где система координат CxbXxbYxbZxb связана с верхним элементом. Так как проекции вектора на сонаправленные оси равны, то последнее выражение можно переписать в виде

J . юЧ + J . ю1.    . юЧ

Т^Вр = ^{Ххв Ххн YxH Z}'^H - I m m - T m m          m m

• ¹⁸                      2                        X_XBY_XB X_XH Y_XH Y_XBZ_XB Y_XH Z_XH Z_XBX_XB Z_XH X_xff ’

если принять, что соответствующие оси систем координат CxbXxbYxbZxb и AxXxhYx‘hZxh сона- правлены.

С учетом (6) и (7) выражение для кинетической энергии верхнего элемента штанги можно записать как

^is = |р1в?1² + ^^ ("М? + J^ ) + ю¹^ (m_XBq_x

+ J_Y* ) + ^ {m^+J . ) 'IB Z_XH                ^Z_XB ■

„• co . to . J . . ю . co . J . « co . ю.

X\B4B XXH YXH YXBZXB YXH ZXH ZXBXXB ZXH XXH

Полная кинетическая энергия штанги равна со QmXBqx-\-J . +J . ) + to. (mXBqx+J . +J . ) + ® • (jnXBqx +J . +J . ') + mXBqx XXH            XXB XXH______YXH 1          YXH______ZXH 1 ZXB ZXH_________

®Y* ^ X* Y* ^ ^X* Y* ®Y* ®7* ^Y*7* ^ ^7* ^—®7* ® Y* ^ 7* Y*      X*

Х\н YXH XXBYXB XXHYXH YXH ZXH YXBZXB YXHZXH ZXH XXH ZXBXXB ZXHXXH

Аналогичные выражения должны быть составлены для каждой штанги механизма.

Для определения проекций угловой скорости на оси системы координат A_XX_XHY*_HZ_XH можно использовать следующие кинематические уравнения:

®xt_H"^H^y_XH ; со . =У\н\ со . = ^ sin/_w .                                   (9)

Л\Н                  чн         £\н

Уравнения (9) выводятся аналогично кинематическим уравнениям Эйлера [5] при условии, что поворот штанги в двухстепенном шарнире А] рассматривается как совокупность двух последовательных поворотов: вокруг связанной со штангой оси А_хХ_хн на угол 9_ХН , вокруг связанной со штангой оси A_XY_XH на угол /_ш.Углы S_XH и у_хн определяют пространственную ориентацию системы координат A_xX_xhY_xhZ_xh относительно некоторой неподвижной системы координат. Пусть в качестве неподвижной выступает система координат A_xX_xhY_xhZ_xh . При решении задач кинематики для заданных значений обобщенных координат q, могут быть определены координаты (х™_н, у™_н ’ ^Z™_H ) точки С_хн (или любой другой точки, принадлежащей нижнему элементу штанги и лежащей на оси A_XZ_XH) в этой неподвижной системе координат. Так как пересчет координат при развороте систем координат на углы д_хн и у_хн описывается произведением

матриц 0 0 > 4osy 0 - sin y^ 0 cos .9 sin i9 ^7- 0 1 0 .0 -sin 19 cos#. 4siny 0 cosy ? то можно записать

^Хс_хн ^=s*ⁿ/i//|^1Сш|; Ус_хн ^-siniS]^ со5/]_Я lA^i^l; y_Cw =cosS_XH cosy_XH |AjC_w|, откуда получаются два простых выражения для определения углов S_XH и у_хн по известным координатам точки С_хн:

„НП            _

У\н = ^агс8ЮТГ7^7; ^н = arctg—.

(Ю)

ZCXH

Продифференцировав (10) по времени:

НП -НП _ НП -НП

/, _ ХС\Н          Q _ZcAH^C\H Усхн2СХН а с 1-х™       у

ХСхн           УСи Чн можно переписать выражения (9) как функции от координат точки Схн :

,™ ..НП _ НП -НП „ _ ²с_хнУс_хн ^С\_Н ^ZC\h со • —           :       5

Х\н НП 2 НП 2

Усхн *zcXH

1-

X™ ХСХн

хнп ХС\н

^; “V ⁼ "'Г^Л.....

™ пас 12-х™ уН-гин! xCw

НП -НП _ НП -НП

0) , г\н

ХС\Н

(П)

у"?„²«™„² 1^А'^С“1'

Выражения (11) входят в уравнение (8) кинетической энергии штанги. При составлении уравнений Лагранжа 2-го рода потребуется дифференцирование (8) по обобщенным координатам и скоростям. Координаты (х™ , у™_н , z™_H) , входящие в (11), являются функциями обобщенных координат q, , однако получение этих функций в явном виде затруднительно. Поэтому целесообразно представить проекции угловой скорости в следующем виде:

8ю.           дсп.           8®.

tox*XH = 5~^-’ Х =        ®zXH а уравнения (11) использовать для численного определения частных производных угловых ско-дсох.   8®у.   8юг.

ростей---—,---—,---—. При этом координаты и скорости, входящие в (11), определяются

8q,      Sq, 8q, численно при решении прямой задачи кинематики как функции обобщенных координат q,.

Кинетическая энергия Т_пп подвижной платформы как абсолютно твердого тела будет определяться следующим образом:

m _ грЦ.М , прВр

1ПП ~1ПП ^ПП’ где Т^ - кинетическая энергия движения центра масс подвижной платформы в предположении, что в нем сосредоточена вся масса платформы; Т^ - кинетическая энергия вращения платформы вокруг центра масс. Аналогично (5) можно записать:

тЦ-^м               I²

^ПП - ^nnVCnn! ’ где mnn - масса платформы; vCnn - скорость центра масс платформы. Величину |тСда | целесообразно выразить через обобщенные координаты qe следующим образом:

i?c>z^,=z:%L                        («I где модуль радиус-вектора центра масс подвижной платформы УСпп | определяется через координаты центра масс (хСпп, Успп, 2спп) в нек0Т0Р°й неподвижной системе координат, например, OXYZ: ^гСпп | = ^х^пп + у1-пп + z^nn . Входящие в (12) частные производные находятся из решения задач кинематики. При моделировании координаты (хСпп, уСпп, zc ) можно принять в качестве выходных координат механизма.

Свяжем с подвижной платформой систему координат C_nnX'Y'Z' (см. рис. 1), такую, что ее оси являются главными осями инерции платформы. Если известны компоненты тензора инерции подвижной платформы в точке С_пп относительно осей этой системы координат, то аналогично (3) можно записать, что

J , ю1, +J, ю2, +J, ®2, уВр _ х'пп Х'пп Y'nn Y'nn Z'nn Z'nn nn                     2                   > где проекции вектора угловой скорости могут быть определены в виде

® X'nn

а® ,                 а® ,

R™q. ’ ®Y. =          ’03г dq j       Y пп у dq/ z пп

a®

Для определения частных производных в (13) можно использовать кинематические уравнения Эйлера [5]:

^юх'_пп ”Фпп s™ ^пп sin^ _пп + 9_ПП cos ср_пп; ю_у._пп =i//_nnsm9_nncos

nn -9_nns"m

nn;

®z’nn ~^пп С08^лл +Фпп где углы прецессии у/пп, нутации Эпп и чистого вращения фпп определяют разворот системы координат CnnX'Y'Z' (соответственно, разворот платформы) относительно осей некоторой неподвижной системы координат, например, OXYZ. При моделировании целесообразно принять эти углы в качестве выходных координат механизма; связь этих углов с обобщенными координатами определяется из решения задач кинематики.

Полная кинетическая энергия элементов механизма равна Т^ = 5^^+^7л >где z = l,6.

Найдем производные кинетической энергии, необходимые для записи уравнений Лагранжа:

ay _ у ат, атпп 8^ ^ 8q j Bq j

= qjT4miB*mnn

STcnn aq.

IV^™!^;

d dT^ _

dt Bq

d . 4.

= д qj4m‘B+m,

д гсял Лд гс .

9q,

Bq,

Bq,

■пп

5|гг I 6 gif I lymzl V^ l£mz| "

q.;

BTy ar aq, ^aq.

am 6                     B®„. 6

aq, ^        ^ XiH eq, tl

6 3®.

xiH

Sq»

qn+miBqj £

6 a® .

XiH

-|2

qn

a®v. t + (miBq^J . +J.

Qq

6 a®.

”1 YiH

6 а®. qn+^iBqj ^-x^qn

-12

1                       а®.

6 а®.

м 8qiX

q^m^qj ^

6 a®.

²Ш Sq_iX

- 2

9,1 Y* Y* Y* V* ^xiB^Y,B X_iHYiH

a®.

x_iH у aq, h

6 a®.

YiH

Sqn

9,1

814 4^X1, „

&1, IS &,« "

+ VY* 7* "*" JY* 7* ^

YiHzm Qq

а®. 6 а®.

У,н у ZiH. м aq_n

dm. 6 a®.

aq.

YiH

q^ + У

ziBxiB ziHxiH

x

a®. 6 a®.

^ZiH у X_iH 8q, 8q_iXⁿ

аю. aq.

6 a®.

a® , '         X’nn x'nn dq

6 a®

a®

Г ^Y'nn ^rnn dq.

6 a®.

X

Y’nn

a®.

Sqn

9,1 + J.

2'nn

z'nn Bq

6 a® C ^ пп

8qn

qt\-

Смирнов В.А., Петрова Л.Н.                                  Динамическая модель механизма___________________________________________________________с параллельной кинематикой

Обобщенные силы Q₍, присутствующие в рассматриваемой динамической системе, определяются активными силами в приводах, силами веса элементов штанг и подвижной платформы, а также некоторой внешней силой, например, силой резания.

Пусть внешняя сила Р_вн приложена в точке С_вн (см. рис. 1) с координатами (х'_вн 1 Увн 1 ^z'bh ) ^в связанной с подвижной платформой системе координат С _nnX'Y’Z' ; направление действия этой силы определяется направляющими косинусами 1_ВН, т_вн, п_вн в неподвижной системе координат, например, OXYZ . Элементарная работа этой силы равна скалярному произведению вектора силы на изменение радиус-вектора точки С_вн ее приложения: ЗА_ВН⁼ ^вн ' ^с_вн • Если изменение радиус-вектора точки С_вн вызвано изменением обобщенной

координаты q_x, то можно записать:

Ж                         _(^9хвн 7 , ^вн , ^9z.

Свн "" ^Свн иУсвн №свн -

5^1

где i , j, k - единичные векторы системы координат OXYZ ; частные производные по обобщенной координате рассчитываются с использованием уравнений кинематики. Элементарная работа в этом случае равна:

SA_BH - Zj

i ®^xbh , 9y_BH       8z_BH

BH -  + mBH -   + "BH a

5?i d^i 5q_x

что позволяет записать составляющую обобщенной силы ^, определяемую внешней силой:

^_Р_ВН О h

' ®^хвн , ™ 8у_вн         dz_BH

ВН - +тВН -   + ПВНЕШ а

9q\ oqx            oqx

Ip I

\ГВНЕШ | '

Составляющая обобщенной силы Q_x , определяемая силой веса подвижной платформы, запишется следующим образом:

8zCmi й Рпп = -Х^™пп8,

• -    ™ oq_x

где z_Cnn - соответствующая координата центра масс подвижной платформы в неподвижной системе координат OXYZ ; g - модуль ускорения свободного падения.

Составляющие, определяемые силами веса элементов раздвижных штанг, равны: g_z™            q_z™       _

61 Рпп             й Рпп =-Х^^т>в8. z = l,6,

• -    oq_x            ~ oq_x

где частные производные рассчитываются для координат соответствующих центров масс в любой неподвижной системе координат, оси которой сонаправлены осям OXYZ.

Выражение для j-Й обобщенной силы примет следующий вид:

г ^9хвн , ^Увн , вн _а^{+ т}вн ^{+ п}вн 8q,         9q.

^ВН

dq

вн

^ пп V ^j

т,

« 94j

где Р_} - активная сила, соответствующая j-й обобщенной координате.

Активные силы могут задаваться через статические Р, = PCTjQu pqpq ^ или динамические TjPj + Р, = PCTJ (и}, q}, q}) характеристики приводов [6], где и3 - управляющее воздействие, т} - постоянная времени привода.

Полученные выражения для обобщенных сил и производных кинетической энергии после подстановки в (1) позволяют получить 6 (по числу степеней свободы) дифференциальных уравнения 2-го порядка, описывающих динамику рассмотренной системы.