Динамическая модель спецстанка для сверления глубоких отверстий в трубных досках большого диаметра из труднообрабатываемых материалов

Введение. Одной из особенностей обработки трубных досок большого диаметра на радиальносверлильных спецстанках для сверления глубоких отверстий на основе станков типа «Чепель» является возникновение в процессе обработки автоколебаний системы СПИД в вертикальном направлении. Возникновение автоколебаний является следствием относительно малой жесткости как преобразующей системы станка, так и обрабатываемой заготовки [1]. Практика эксплуатации описанного станочного оборудования показала, что возникающие автоколебания, в зависимости от частоты и амплитуды, могут иметь и благотворное влияние на процесс обработки и негативное.

Цель исследования – повышение технологической надежности процесса сверления отверстий (в том числе, глубоких) в трубных досках большого диаметра из труднообрабатываемых материалов, а также в трубных досках из слоистых материалов на спецстанках, изготовленных на основе радиально-сверлильных станков «Чепель» с использованием твердосплавных сверл с внутренней подачей масляной СОЖ.

Поставленная цель может быть достигнута в результате решения комплекса объемных научных и технологических задач, составляющих содержание исследования:

– разработка динамической математической модели подсистемы инструмента спецстанка;

– разработка динамической математической модели подсистемы заготовки и рабочего стола спецстанка;

– разработка математической модели процесса сверления глубоких отверстий, учитывающей особенности сверления труднообрабатываемых материалов;

– построение объединенной динамической математической модели, включающей в себя вышеупомянутые модели;

– идентификация параметров математической модели по результатам экспериментальных исследований, проведенных при сверлении образцов трубных досок, а также по результатам непосредственных измерений и расчетов;

– аналитическое и численное, с использованием методов имитационного моделирования, исследование динамических свойств объединенной модели. Определение возможности и условий возникновения автоколебаний в системе сверления;

– разработка методов выбора режимов обработки для получения возможности управления автоколебательными режимами при глубоком сверлении труднообрабатываемых материалов.

В ходе исследования определены:

• –    возможность и условия возникновения автоколебаний в модели системы сверления;

• –    наблюдаемость и управляемость модели по управляющим воздействиям и параметрам системы управления;

• –    области устойчивости и области возникновения устойчивых автоколебаний в динамической системе сверления.

В исследовании представлено решение первой из поставленных задач – построение динамической математической модели станка для сверления глубоких отверстий.

Математическая модель преобразующей подсистемы спецстанка. Внешний вид радиально-сверлильного станка RF-51 «Чепель», на базе которого создан спецстанок для сверления глубоких отверстий, приведен на рис. 1. Станок состоит из колонны, траверсы, сверлильной бабки. На рабочем столе расположен обрабатываемый пакет перегородок пароконденсатора. Упрощенная кинематическая схема станка приведена на рис. 2.

Рис. 1. Внешний вид радиально-сверлильного станка RF-51 «Чепель»

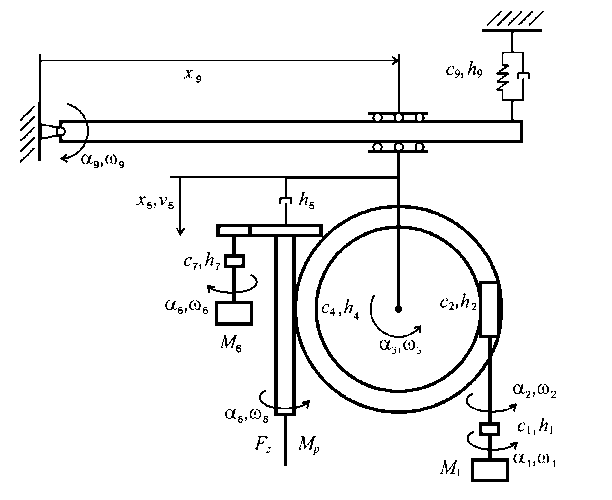
Рис. 2. Кинематическая схема модели станка

Математическая модель, включающая в себя все кинематические подсистемы станка, получается достаточно объемной (станочная система имеет не менее 7 степеней свободы). Однако для анализа устойчивости системы и определения закономерностей возникновения автоколебаний, связанных с взаимовлиянием подсистем через процесс обработки, она может быть существенно упрощена. В частности, динамическими процессами в зацеплениях между червячной передачей и зубчатым колесом можно пренебречь без изменения качественного поведения системы, сведя их к эквивалентному моменту инерции J _{2 e} . Также можно пренебречь динамическими процессами в редукторе между приводом главного движения и шпинделем, рассматривая редуктор как идеальное усилительное звено. Подсистему закрепления сверлильной бабки на траверсе можно заменить эквивалентной упруго-диссипативной системой, учитывая изменение плеча рычага переменными коэффициентами. Преобразованная эквивалентная кинематическая схема спецстанка показана на рис. 3.

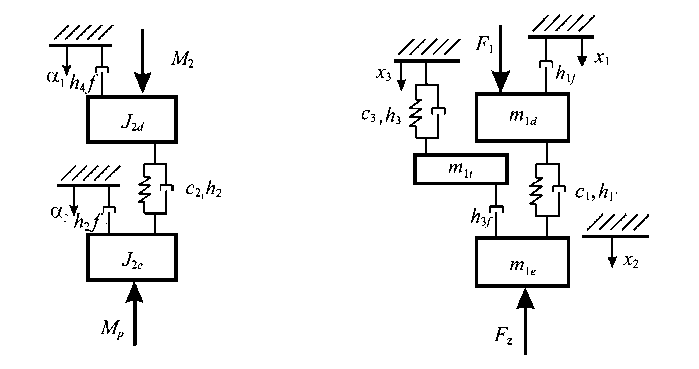
а)                                       б)

Рис. 3. Упрощенные кинематические схемы подсистемы привода главного движения ( а ) и подсистемы подачи ( б )

Подсистема привода главного движения. Механическая подсистема вращения шпинделя характеризуется углом поворота вала двигателя а 1 и скоростью вращения и 1 , вращательным моментом M ₂ , приложенным к ротору, моментом инерции ротора электродвигателя и упругой полумуфты сочленения со шпинделем станка J _{2 d} , коэффициентом диссипации в подшипниках двигателя h 6 f , жесткостью и диссипацией в упругой муфте с₇ и h 7 , углом поворота шпинделя а ₈

и скоростью его вращения ю ₈ , моментом инерции шпинделя станка J ₈ , коэффициентом диссипации в подшипниках шпинделя h _{8 f} и моментом сопротивления вращению, формируемому процессом резания M ₈ . Система уравнений, описывающая вращение шпинделя, имеет вид:

d а

"dT "ю1, dt j  [M2  c2 (а1  а 2 )  h2 (®1  ®2 )  h4f ®1 ] ,

• 1    ,

d а

= О , dt 2

""d ^" = — [ С 2 ^(а 1 ^-а 2 ) + h 2 (/ О ^-® 2 ^)- h 2 _f ® 2 ^- M p ] .

Подсистема сервопривода. Упруго-диссипативная подсистема c коэффициентами жесткости c ₁ и диссипации h ₁ обеспечивает передачу усилия от сервопривода на шпиндель, обеспечивая его поступательное перемещение. Принятые обозначения: h _{1 f} – коэффициент диссипации в подшипниках; x ₁ – координата подвижной части сервопривода; v ₁ – скорость; x ₂ – координата поступательного перемещения шпинделя; v ₂ – скорость; m _{1 d} – эквивалентная масса подвижной части сервопривода; m _{1 e} – эквивалентная масса подвижной части шпинделя; F ₁ – усилие, действующее на сервопривод со стороны серводвигателя [2]; F_z – усилие, действующее на шпиндель со стороны процесса обработки. Влияние траверсы учитывается коэффициентами жесткости и диссипации c ₃ и h ₃ и эквивалентной массой m _{1 t} . Демпфирующий коэффициент h _{3 f} учитывает потерю энергии в пластинчатой пружине в подсистеме подвеса шпинделя.

Уравнения динамики подсистемы имеют вид:

dx 1

v”

dvr = — [ F1 - cl ( xl - x 2 )-hl ( vl - v2 )-hl fvl ], dt   m1d dx

= v 2 ,

<

dt

dv2- = — ^ cl ( xl - x 2 ) + hl (vl - v2 )-hl f ( v2 - vз )-Fz ], dt   m1e dx

= v3, dt dv 1

—- = —I - с ( x, dt m i t ^{L 3 ( 3}

-

x 2 ) - h ( ^V 3

-

v 2 ) + h l f ( v 2

-

Моделирование процесса резания. Процесс резания выступает нелинейным элементом, объединяющим подсистемы сверлильного станка. Поэтому построение корректной модели процесса сверления является принципиально важным для достижения поставленной цели исследования.

Сила резания в первом приближении может быть описана [3] выражением: IFp\ =ptpSоб , где p - коэффициент резания; tp - ширина срезаемого слоя; Sоб - оборотная подача.

Осевая составляющая силы резания в этом случае составляет F_z = X _z p t _p S об , момент сопротивления вращению M _p = X_Tp t _p S _об r , где r - радиус сверла. Учитывая, что для спиральных сверл t _p = r , имеем:

F = X z p S об r ,   M p = X_Tp S об r ² .

При равномерном сверлении S _об определяется отношением скорости вертикальной подачи к частоте вращения сверла (в единицах СИ):

_S =^ v_ ^об 180 to₈ , 8

т. е. зависимость оборотной подачи от скорости подачи и частоты вращения формирует нелинейную связь между подсистемами станка через силовые характеристики процесса резания:

n v_{9    2}

MD =XTp---— r2, p       180rn2

c        n v₂

F, = X о---— z       180rn2

r .

Для понимания процессов, приводящих к заклиниванию при глубоком сверлении, принципиальное значение имеет взаимовлияние приводов [4, 5]. При этом можно пренебречь подсистемой траверсы и промежуточных упругих соединений, сосредоточившись на подсистемах приводов:

d m2 dt dv2 dt

J 2 e

m _{1 e}

d m2 dt dv2 dt

^П v2   2

M_A — h ,m_? - X о — r ^{1    2 f 2 T} 180 m ₂

F₂ - h v 2

-     n v₂

X.p — 180 m ,

,

J 2

m 1 e

M i — h 2 f m, — ki —— m2

F₂ — h 1 v 2 — k 2 " v ²"

m ₂

В самом простом случае практический интерес представляет анализ области существования стационарных положительных значений скорости подачи и скорости вращения шпинделя в зависимости от сил, приложенных со стороны приводов. Для этого уравнение статики для системы (7) необходимо разрешить относительно координат состояния. После очевидных преобразований и подстановок получаем уравнение для скорости главного движения:

h i h f m 2 + ( h 2 f k 2 — h i M 1 ) m 2 + k i F 2 — k 2 M 1 = 0 , (8)

^k 2 _— ^M i _— 4 ^k 1 ^F 2   ^k 2 ^M 1

_v h i     h 2 _f J            h i h 2 _f

m (ⁱ,2⁾ =— ¹ f k 2 — M i 1± 1

• ²       2 ( h i h 2 f J 4

  Необходимым условием существования сверления является неотрицательность дискриминанта. Это позволяет определить возможные значения скорости вращения в зависимости от сил, прикладываемых со стороны привода:

  

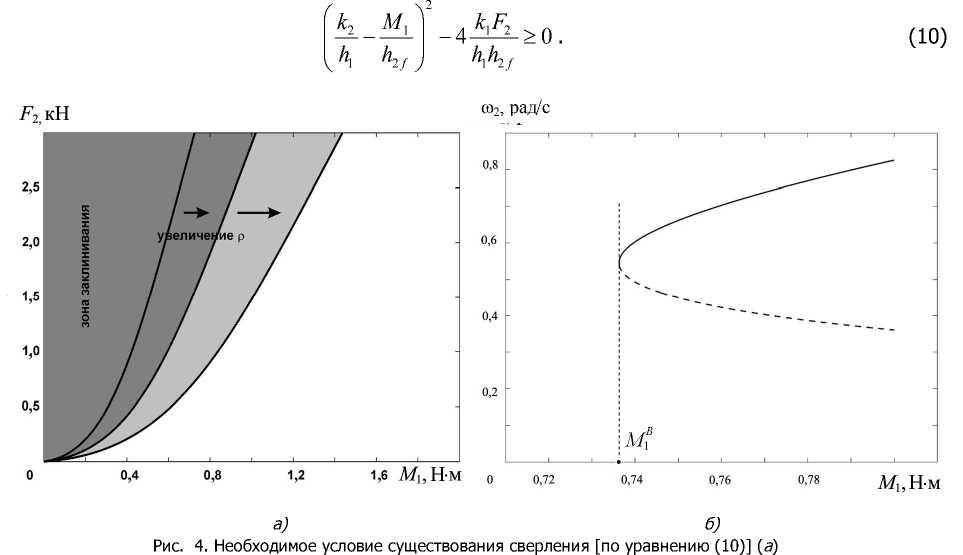
  и частота вращения привода главного движения [действительные корни уравнения (9)] ( б )

  
  

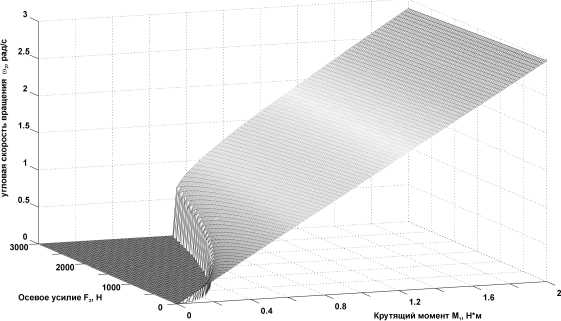
  Значение M B * 0,7353 крутящего момента на приводе главного движения соответствует (при данной осевой нагрузке на сверло) бифуркационному значению, при котором сверление становится возможным. Диаграммы стационарных точек – зависимость скорости вращения шпинделя от M 1 и F ₂ приведены на рис. 5.

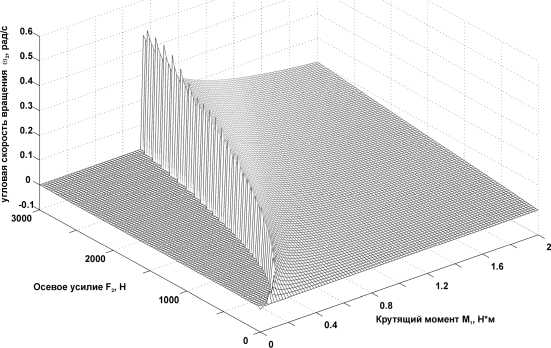
м 2¹)

® 2²’

Рис. 5. Зависимость скорости вращения шпинделя [уравнение (9)] от M 1 и F 2

Следующий вопрос, который должен быть исследован – устойчивость стационарных точек.

Линеаризуя (7) в стационарных точках для значений M 1* и F , , получаем системную матрицу:

A =

(

J 2 e

V

- h f ⁺

V

*

Jv^ ( ГО ) ’ J

^k 2 v 2

m l e ( ® 2 ) ²

m

1 e

^ ^k 1

J 2 e ®2

-

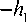
V

k^ ^

^ГО 2 J

J

Для значений силовых воздействий M 1 = 0,76 Н - м и F 2 = 3000 Н определяем стационарные частоты вращения m 2¹) = 0,4145 и m 2²) = 0,7174 , скорости v 21) = 0,0101 и v 22) = 0,0102 и, таким образом, получаем явный вид системных матриц:

A^J21,9 2090 )

( 1,5    - 3145 _v

A (2)=H2,0

, I 0,5

1208 2

- 3048_v

.

Матрица A ^{( 1 )} имеет собственные числа Х^{( 1 )} = 22,8

и Х 2¹ ) =- 3146 и соответствует неустой-

чивому положению равновесия (нижняя ветвь на рис. 4,б), матрица A ^{( 2 )} имеет собственные числа Х^{( 2 )}=- 11,8 и /.'? - 3049 и соответствует устойчивому положению равновесия (верхняя ветвь на рис. 4, б ).

Фазовая траектория нелинейной системы сверления, полученная численным моделированием и подтверждающая приведенные выше рассуждения и выкладки, показана на рис. 6.

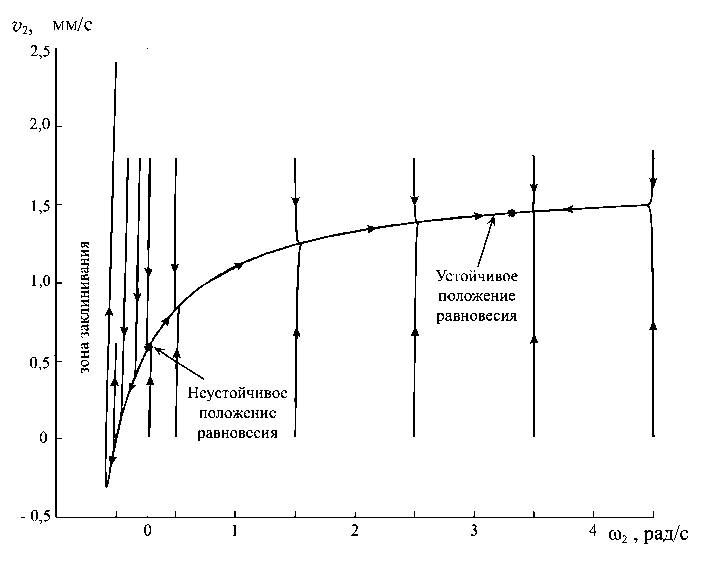
Рис. 6. Фазовый портрет системы сверления для M * = 2,75 Н - м, F 2* = 500 Н и координатами { m ₂, v ₂ } (рад/с, мм/с) устойчивой {3,31; 1,4} и неустойчивой {0,28; 0,6} точек соответственно

Заключение. Изложена процедура построения математической модели спецстанка для сверления глубоких отверстий в труднообрабатываемых и гетерогенных материалах. В ходе проведения работ были получены следующие результаты:

– получена упрощенная математическая модель динамики сверления на спецстанке для сверления глубоких отверстий;

• –    при анализе модели определены условия возможности сверления (существование и величина бифуркационного параметра) в зависимости от характеристик преобразующей системы спецстанка и силовых воздействий приводов подачи и главного движения;

• –    построены области существования сверления в зависимости от силовых воздействий приводов подачи и главного движения;

• –    проведено имитационное моделирование и получен пример фазового портрета, подтверждающего правильность проведенных аналитических вычислений.