Динамическая осесимметричная задача прямого пьезоэффекта для круглой биморфной пластины
Автор: Шляхин Д.А.
Статья в выпуске: 1, 2017 года.
Бесплатный доступ
Рассматривается динамическая осесимметричная задача для круглой биморфной конструкции, состоящей из металлической подложки и пьезокерамической аксиально поляризованной пластины. Ее изгибные колебания осуществляются за счет действия на торцевой поверхности механической нагрузки (нормальных напряжений), являющейся произвольной функцией радиальной координаты и времени. Учитывается жесткое и шарнирное закрепление цилиндрической поверхности пластины. Исходные расчетные соотношения сформулированы для пьезокерамического материала с гексагональной кристаллической решеткой класса 6 mm. Для решения задачи теории электроупругости в трехмерной постановке используются конечные интегральные преобразования Ханкеля по аксиальной координате и обобщенное преобразование (КИП) по радиальной переменной. При этом на каждом этапе решения проводится процедура стандартизации, которая позволяет реализовать соответствующий алгоритм преобразования. В первом случае краевые условия представляются в смешанной форме, а во втором приводятся к однородным путем введения вспомогательных функций. Данный подход позволяет получить точные, в рамках используемых моделей, расчетные соотношения в наиболее общем виде. Построенное замкнутое решение позволяет определить частотный спектр собственных осесимметричных колебаний, напряженно-деформированное состояние и характер изменения индуцируемого электрического поля биморфной пластины. Это дает возможность на основании анализа связанности электрических и механических полей напряжений научно обосновать конструктивные решения проектируемых приборов, определить способ фиксации электрического сигнала, подобрать все геометрические, а также физические характеристики типовых элементов пьезокерамических преобразователей. Разработанный алгоритм решения позволяет также решать задачи теории упругости и электроупругости для круглых толстых и тонких пластин с произвольным количеством слоев при наиболее общих условиях загружения без использования кинематических гипотез.
Биморфная пластина, задача прямого пьезоэффекта, теория электроупругости, динамическая нагрузка, конечные интегральные преобразования
Короткий адрес: https://sciup.org/146211660
IDR: 146211660 | УДК: 539.3 | DOI: 10.15593/perm.mech/2017.1.10
Текст научной статьи Динамическая осесимметричная задача прямого пьезоэффекта для круглой биморфной пластины
В различных технических устройствах используются пьезокерамические датчики в виде тонких биморфных пластин [1–8]. Как правило, они состоят из двух жестко соединенных круглых пьезокерамических пластин с противоположной или параллельной направленностью вектора поляризации. Для повышения механической прочности в рассматриваемой конструкции применяется металлическая подложка [9, 10].
Расчет пьезокерамических многослойных конструкций в основном выполняется с помощью прикладных теорий для тонких пластин [11–13], в которых кинематические гипотезы дополняются аналогичными допущениями о характере изменения электрического поля [14–21]. Для более полного учета связанности физических полей в многослойных пьезокерамических пластинах в работах [22, 23] было проведено исследование и получено замкнутое решение нестационарной задачи обратного пьезоэффекта в трехмерной постановке. На основании численных результатов сделан вывод, что при аксиальной поляризации материала напряженность электрического поля по высоте тонкой пластины изменяется по линейному закону. Кроме того, установлено, что при использовании сплошного электродного покрытия касательными напряжениями, возникающими в конструкции, можно пренебречь.
В настоящей работе рассматривается нестационарная задача прямого пьезоэффекта для асимметричной (отсутствует симметрия физических свойств материала относительно нейтральной плоскости) сплошной биморфной пластины с жестким, а также шарнирным закреплением ее цилиндрической поверхности.
1. Постановка задачи
Пусть круглая двухслойная пластина, занимающая в цилиндрической системе координат ( r * , 0 , z * ) область Q : { 0 < r * < b , 0 < 0 < 2 п , 0 < z * < h * } , состоит из пьезокерамического элемента высотой h * , выполненного из аксиально поляризованного (электроупру-гого) материала с гексагональной кристаллической решеткой класса 6mm , и металлической (упругой) заземленной подложки толщиной h 2 ( h * = h * + h . ). Изгибные осесимметричные колебания возбуждаются за счет действия на лицевой поверхности конструкции ( z * = 0) механической динамической нагрузки (нормальных напряжений) q* ( r * , t * ) , являющейся произвольной функцией радиальной координаты r * и времени t * (рис. 1). Подключение электродов к измерительному прибору позволяет зафиксировать величину и форму электрического напряжения V * ( t * ) . Рассматриваются случаи жесткого, а также шарнирного закрепления цилиндрической поверхности конструкции.
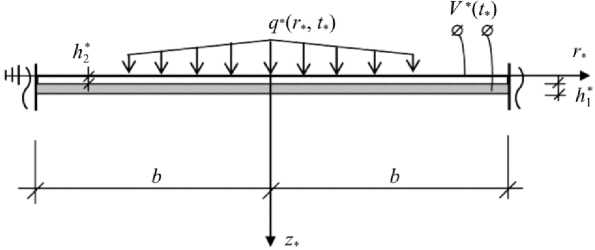
Рис. 1. Биморфная пластина
Fig. 1. Bimorph plate
Дифференциальные уравнения движения и электростатики в цилиндрической системе координат и безразмерной форме имеют следующий вид [24, 25] :
5 V/ ,4- C 55 8 2 U 4-( C'3 ) + C “ ) 8 W 4- ( e =■ + e 15 ) 8 2 Ф ф( ' ) 8 ^
(1.1)
= 0,
V U + + +
5r Су 5z2 С1у 5r5z e33 5rdz
C55!V5W+c33) 52w ,(C3)+C55))£vU+ei5v^+5^—Ф(s) 52w Ch) 5r C111) 5z2 C11) 5z e33 5r 5z2
(e31 + e15) £уU + ei5V5W + 52W - C^ у5ф — С^зз 52ф e33 5z e33 5 r 5z2 e323 5r e323
При исследовании упругой среды (s = 1) система (1.1) состоит только из уравнений движения, сфор- мулированных относительно компонент вектора перемещений.
Граничные условия на цилиндрической поверхности определяются равенствами r = 0,1 W (0, z, t ) Drr=1 C^Sn 5ф e2 9 r e_ (9 W 9 U + ^51 — + — e33V 9r 9z жесткое защемление W(1,z,t) = 0, U(1,z,t) = 0; шарнирное закрепление W (1, z, t ) = 0 CTrr^r=1 C^ 9U C"?U -£ 9 W e31дф -1(1’ 9r C1(1) r C1(1) 9z e339z (1.2) (1.3) (1.4) Первые три неравенства (1.2) являются условиями регулярности решения для сплошной пластины, а последнее учитывает отсутствие электродного покрытия. Граничные условия по аксиальной координате формулируются следующим образом: z = 0 z = h 2 z = h CTzz = V U + -S’ C 32 9 W -M 9z = q, ctrz —2(9 W 9 U ) A 55^1= 0 -11’ V dr 9z J -111VU+C33) d W . •" -« -W 5z 5z V|z+0 -2 (9 W 9U ) e15 бф JJ । । 15 -11’ V 5r 9z J e335r (-£v y+c£8W+* V di1U di) sz & A J|z-0 -52’ ( 5 W 9 U Г(1)\ 9r 9z C11 V dr dz J|z-0 U (z + 0) = U (z - 0), W(z + 0) = W (z - 0), ф(z + 0) = 0; „ - -n’v,,C">8W Эф CT„ = --7— V U +--7—--1--= 0, -11’ -11’ 9z 9z (1.5) (1.6) (1.7) CT rz -5J^(SW +8U^+8ф= 0D =_C^8ф +e,!VU+aW = 0. C,i : V dr 9z J e339r , z e323 5z e33 5z Равенства (1.6) являются условиями совместности напряжений, деформаций и заземления подложки. Кроме того, последнее равенство (1.7) учитывает подключение электро-дированной поверхности пьезокерамической пластины к измерительному прибору с большим входным сопротивлением, что соответствует режиму «холостого хода» (отсутствию свободных электрических зарядов). Начальные условия задаются в общем виде и позволяют определить состояние пластины в момент приложения нагрузки: t = 0 U(r,z,0) = U0(r,z), -— = U0 (r,z), (1.8) dt \t=0 d W W (r, z ,0) = W> (r, z), — = W0 (r, z). dt \t=0 Перевод размерных функций и переменных в безразмерные величины производится по формулам {U,W,U0,U0,Wo,Wo,r,z,h,hl,h2} = {u*,W*,U0,U0,W^,w,r*,z*,h*,h*,h0}/b , a- q— z z -~tb~\ (2) /o(2) q = (1) , v(r, z, t) v (r, z, t) e33 (bC11 ) , t t*b \C11 / р• C11 В равенствах (1.1)-(1.8) приняты следующие обозначения: U*(r*, z*, t*), W*(r*, z*, t*), cpm (r*,z„ t*) - компоненты вектора перемещений и тензора напряжений (p, m = r, z); Dr (r*, z*, t*), Dz (r*, z„ t*), v* (r*, z*, t*) - компоненты вектора индукции и потенциал электрического поля; emk, 811, 833- пьезомодули и коэффициенты диэлектрической проницаемости электроупругого материала (m, к = 1,5); р(s), Cmk - объемная плотность, модули упругости электроупругого (s = 1) и упругого (s = 2) материалов; U*, Uo*, Wo*, Wo* - извест- C(2)р(1) ные в начальный момент времени перемещения, скорости перемещений; Ф(1)= “ р , С Р2) Ф(2)= 1, V = —+ 1. dr r Соотношения (1.1)-(1.8) представляют математическую формулировку рассматриваемой краевой задачи электроупругости.
2. Построение общего решения На первом этапе решения краевой задачи (1.1)-(1.8) используется метод конечных интегральных преобразований Ханкеля по радиальной координате r [26]. При этом данное преобразование позволяет удовлетворить только смешанные граничные условия. Для выполнения данного требования необходимо: - для жесткого закрепления первое равенство (1.3) заменить на условие отсутствия на цилиндрических поверхностях пластины (r = 1) касательных напряжений: c = c55) (aW +8U >+e^ dv= (2.1) rz|r=1 C(1) v dr dz J e33 dr ’ - для шарнирного закрепления последнее соотношение (1.2) заменить условием наличия потенциала электрического поля ф1 (z, t) на цилиндрической поверхности при r = 1: v(1,z,t) = V1 (z,t). (2.2) Кроме того, вводятся новые функции u (r, z, t), w(r, z, t), v(r, z, t), связанные с U(r, z, t), W (r, z, t) , v(r, z, t) соотношениями U (r, z, t) = N1 ( r, z, t) H (z - h2) + N2( r, t) + u (r, z, t), (2.3) W(r,z,t) = P1 (t) + w(r,z,t), v(r,z,t) = V1 (z,t) + v(r,z,t), Ni (r, z, t ) = - e31 2e33 5ф1 (z, t) 5z r j1 = 0, Ф1к=h2 = 0), N2 (r, t ) = ( r2- r) q (r, t). k 5Z | z=h 2 у Здесь H(...)-единичная функция Хэвисайда [27]; P1 (t),ф1(z,t) - неизвестные функции, определяемые в процессе решения задачи соответственно из условий отсутствия вертикальных перемещений цилиндрической поверхности (r = 1) пластины при z = 0 (первое равенство (1.3)) и радиальной компоненты вектора индукции электрического поля при r = 1 (последнее равенство (1.2)). В результате подстановки (2.3) в (1.1)–(1.8), (2.1), (2.2) получаем новую краевую задачу относительно функций u, w, ф . При этом дифференциальные уравнения (1.1), первое условие (1.5), первые два условия (1.6) и равенства (1.7) становятся неоднородными с правыми частями R1 ^ R3, B1 ^ B6, а начальные условия U0, U0, W0, W0 следует заменить на и0,й^,W0,w0: R = — R2 ' 5 С^) 52 /п 52 ' V + —55Ф(1) 5 r С^ 5z2 512 N1H (z - h 2 )- ( (1V 1 СУ) e31+ С1(1)8зз +( e31 + e15) e31+ 1 R з = С11 ^33 + (e31+e15 ) e31 5 ф1 e 23 5z2 B2 n(2) 13 c (1 С1) (3 r - 2) q - 1 -k — V U - Ф(5) 5 r 5 2U 5 ф1 H (z - h2) + Ф( 5) 5z2 V 27 H (z - h 2 ), B1 = C(1)e 13 e31 C(1)e e N2, 52P 512, П ( 2) 1 - lf(3 r -2) d\ b,=b, = 5z3 5 q, С55^ e31rd ф1 2 С11 ee33 5z С(1) , x c(1)8 +e2e , B4 =-С1У ( 3 r - 2 ) q, B 6 = С11 V e31 дф1- e31(3 r - 2) q, w, = Wo- p=0, С(1) e33 5z e33 wv0 = W^0 - Tpt=0, и0 = U0 - [N1H (z - h2) + N2 ]t=0, ut. = UJ0 - [7N1H (z - h2) + TV2 ]t=0, а краевые условия (1.2)–(1.4) принимают следующий вид: – жесткое закрепление U(1,z,t) = 0, 5W = 0, |ф = 0; (2.4) 5r |z=1 5r\z=1 – шарнирное закрепление W(1,z,t) = 0, ф(1,z,t) = 0 VUr=1 = 0. (2.5) Здесь следует отметить, что в отличие от классической постановки задач теории упругости в настоящем исследовании «жесткое» закрепление (2.4) характеризуется также отсутствием угла поворота. Кроме того, последнее условие (2.5) получается при С^5) = С12). Только в этом случае, в дальнейшем, дополнительные внеинтегральные члены в первом трансформированном уравнении (1.1) равны нулю. Применяем к краевой задаче (1.1)–(1.8), (2.1), (2.2), (2.4), (2.5) относительно функций u, w, ф конечные интегральные преобразования Ханкеля, используя следующие трансформанты: Uh (Л, z, t ) = J u (r, z, t) rJ1 (j,r) dr, (2.6) {Wh (J,z,t),ФH (Л,z,t)}=!{w(r,z,t),Ф(r,z,t)}rJ0 ( j,r)dr, 0 и формулы обращения u (r ,z, t ) = 2£ ' jt)J1 (j,r), (2.7) , =1 S(Jn ) ( ( Л ( п{wH( j", z, t),фh( j", z, t)}r / • A {w (r, z, t), Ф( r, z, t )} = 2L J°(J"r), n=0 S ( Jn ) где J, - положительные нули функций J1 (J,), J0(J,) соответственно при жестком и шарнирном закреплении пластины, расположенные в порядке их возрастания (, = 0, да; Jо = 0); S (J, ) = Jо (j,) при жестком и S (J, ) = J1 (j,) при шарнирном закреплении. В пространстве изображений получаем новую краевую задачу: z = 0 z = h2 z = h -j2uH+ C555) d2u C;) dz2 (;) С2 C^ J-wH+ С333) d2w cf;1dz1 (e31 + e15 ) e33 uH n dwH (e31 + e15) • d Ф Jn dz du H jn du dz e33 dz Ф ,(;) дuH д t2 = R1H (2.8) Сп1 dz e — jnф H + d фH e33 dz2 Ф , (; )д2^Н д t2 R 2 H , e -— J, Wh+ f1 (2) ^13 CW JnuH e33 + d2w dz2 + С(1'е e 7,2Ф h С32^33 d фH e dz2 = R3 H ; Сзз) дw« 33 H C<1>6z (Af) _ f,(2) 13 13 (z + 0) = B1H C552) Г дuH cji> dz jnw (2.9) Cfl) JnuH+ C33)- C(2) dw C55)- C52 pUh C<1> дz - uH Cfl) дz + дф дz = B 2 H , (2.10) - jnw - e33 jnфH = B3 H , (z - 0) = 0, wH (z + 0) - Wh (z - 0) = 0, фh = 0; C (1) ^13 CW JnuH C33) дWj C1>6z дф дz = B4 H (2.11) t = 0 -ЦГди» -W I 5z ^ eis • „ D - JnwH I--JnФH = B5H , / e33 e31 V „ , dwH С1(11)£зз 5фH --jnuH +^27— e33 оz e33 оz = B6 H u (jn , z, 0) = u0H (jn , z) , u (jn , z,0) = u0H (jn , z) , (2.12) wH ( jn , z,0) = woH ( jn , z) , wH ( jn , z,0) = w0H (jn , z) . где {R1H , В3 H , B5 H}=J{ R1, B3, B5 }rJ1 (jnr ) dr, {R 2 H , R3 H , B1H , B 2 H , B4 H , B 6 H}=J{R2 ’ R3, B1, B 2, 00 B4, Be} rJ0 ( jnr) dr. На втором этапе решения используется обобщенный метод конечных интегральных преобразований (КИП) [28] по координате z . Предварительно выполняется процедура стандартизации, связанная с приведением граничных условий (2.9)–(2.11) к однородным, с помощью следующих разложений: uH ( jn , z, t ) = Y1H ( z, t ) + UH ( jn , z, t ) , wH ( jn , z, t) = Y2H (z, t) + WH ( jn , z, t) , (2.13) Ф H ( jn , z, t ) = Y3 H ( z, t ) +X H ( jn , z, t ) . C(1)- C(2) В случае жесткого закрепления, принимая во внимание ф1= 0, B2H = —13—^ 13 BXH , C13 С(1) С(1)е B4H = -^ B1H , B6H = ^1^-31- B1H , имеем C13 C13 e33 Y™ = 0, ¥г„ = h (z)B1„ [1 -H(z-*2)]+f2(z)B,„H(z-h), Y3„ = f3(z)B„H(z-h2), а при шарнирном закреплении, с учетом P1 = N2= 0, получаем Y1H = f (z) B1H [1 Н( zh2 )] + f1 (z) B3HH (zh2 ) , Y2H = f3 (z) B6HH (z - h2 ) , Y3H = f4 (z) B6HH (z - h2 ) . В результате подстановки (2.13) в (2.8)–(2.12), при учете соотношений: при жестком закреплении f(1) f1'( 0) = f1'( h2 ) = -Ц) , (2-14) C33 n ^ 0: f1 (h2) = f2(h2) = f/(h2) = 0, f/(h2) = A1, f,’(h) = A2, f/(h) = A3, f1 (0) = 0, f 2 (h ) = 0 f 3 (h ) = 0, l)/--<1) C(1|fc(1|e +e e 1 fc(1|e -C^e К C,(/C(? ^11 1^13 °33 +e31 e33 / 1^13 e33 ^33 e31 /e33 11 13 A1 C^Cz2), A2 d2) c(1)p 2 , 3 d2) c(1)p +e2 ; 33^13 —13 I- 33 b33 + e33 I —13 I- 33 b33 + e33 I при шарнирном закреплении с (1) f(0) = f(h2) = f'(h) = 0, f'(0) = 77-, (2.15) C33 (1) eL .f2(h2) =f2(h) = 0, f/(h.) = f2'(h) = Д. f,'(h) _ С55 С33 E33 + -33 f•'( h ) = — , ' f’( h ) , fm. ( h 2 ) = fm ’( h2 ) = fm (h ) = 0 (” = 1, 2) C получаем новую краевую задачу относительно функций UH , WH , хH с однородными граничными условиями по координате z . Правые части дифференциальных уравнений (2.8) и начальные условия и,, „, йп н. wn н. wn„ заменяются на R„ ^ F „ , U „, U „ , Wn „.W „ : 0H 0H 0H 0H 1H 3H 0H 0H 0H 0H = Rh 2H C(5) C(5) d2Y (С(з) + С55)) dY e С55 2 С33dY2H13 55 dY1H e152 С) jH С^) dz2 С^) jn dz + -33 - d-YH-+ф( 5) dz2 5 2Y2 H F1H = R1H + i2V -^ d2Y1 H+(С13+ С55) i dY2H . (-3L±-1s) dY3H , ф(5) d211H j"11 H dj) dz2 ' С?5) jn dz ' -33jn dz ' Ф 512 F = R 1 3 H 3H H (-31 + —15 ) dYH ^5 л d YYH Сц^ц 2y С1У£33 d YH jn , JnY2H + ,2 + 2 jnY3H 2 > 2 e33 dz e33 dz e33 e33 dz U0 H u0 H(jn w z ) Y! H11=0, U0 H Ul0 H(jn w z ) Y1H11=0 , W0H = w0H(Jn W z) — Y2H11=0 w WoH = ^w0H(Jn , z ) —Y2H11=0 • Функции f1 (z)^ f 4 (z) w входящие в разложения (2.13)w определяются с помощью следующих равенств: k fm ( z )=Е apz-1 ( m = 1w4) w (2.16) p=1 где ap - постоянные; k - параметрw соответствующий количеству граничных условий для функций fm (z) • Подстановка (2.16) в (2.14)w(2.15) позволяет определить функции fm (z): – жесткое закрепление .f4 (z ) = 0; 7(1) A n = 0 f1 ( Z ) = -(2y( Z - h 2 ) w f3 ( z ) = —( z2 - 2 h 2 z + h 22 ) w C33 2h1 f, ( z) =( 2 h1) 1{(A2 - A1) z2+ 2 ( A1 h - A2h2) z + h2[ A1 ( h2- 2 h) + A2 h2]}; n ф 0 fx ( z ) = C(1) / C11 3 C32) К2 ( - 3 h2z2+ h22z), f2 ( z) = hl 2{( Ax+A2 ) z3-[(2Ax+A2) h+( Ax+ 2A2 ) h2 J z2 + +[ Ax h2+ A h 2 + 2 (Ax + A2) hh2J z - hh2(Ax h + A2h2)}, A f, (z) = —3 Гz3 —(h + 2h2) z2 + h2 (2h + h2) z — hh2 J; – шарнирное закрепление C(x) C(x) f■ ( z ) = Г Л ( z3 - 2 h 2 z 2 + h 2 z ) , f4 ( z ) = - Д f3 ( z ) , C33h2 C11 C f2 ( z ) = C^ [ 2 z — 3 ( h + h 2 ) z +( h + h 2 + 4 hh 2 ) z — hh 2 ( h + h 2 )] , f3 ( z ) = 2 e33 ( С33833 + e33) h Начально-краевую задачу (2.8)-(2Л2) относительно функций UH, WH, хH решаем, используя обобщенный метод конечных интегральных преобразований (КИП) [28] с использованием неизвестных трансформанты G (Xin, n, t) и компонент Kx(Xin, z), K2(Xin, z), K3(Xin, z) вектор-функции ядра преобразования (Xin - положительные параметры, образующие счетное множество (i = x, ^)). Общее решение краевой задачи (2.8)-(2Д2) для электроупругого (s = x) и упругого (s = 2) слоев представлено в работах автора [22, 29, 30]. Здесь следует отметить, что в отличие от стандартной процедуры разложения по собственным функциям [26] метод КИП [28] позволяет в процессе решения динамической задачи определить частоты и формы собственных колебаний конструкции. Окончательные выражения функций U(r,z,t), W(r,z,t) , ф(r,z,t) получим, применяя последовательно формулы обращения КИП [28] и метод конечных преобразований Ханкеля (2.7). В результате с учетом (2.3), (2.13) имеем ^ Jxijnr) YxH (z, t )+:Ё G„K „n|Kn| ^ (Jn) L i=x U (r, z, t) = Nx (r, z, t) H (z — h2) + N2 (r, t) + 2^ n=x J„( J r\V W (r ,z, t ) = Px (t)+ -V ^-2). Y2 H (z, t ) + £ GnK 2in||Kin|| , (2.17) "-02 (Jn) L '-x J ф(r,z, t) = 9x (z, t) + 2jr Jokjnrl Г Y3H (z, t) + jr GinK3in IKin I n=0 2 (Jn) L i=x Заключительным этапом исследования является определение неизвестных функций P1 (t), Ф1 (z, t). В случае жесткого закрепления пластины, когда ф1 (z, t ) = 0, функция P1 (t) определяется из условия отсутствия вертикальных перемещений цилиндрической поверхности пластины при z = 0 и на основании (2.17) принимает вид да да P (t ) = —2Z J0 (j. )—1 Z GK. (А. ,0)1 И Г2- (2.18) n=0 i=1 При шарнирном закреплении P1 (t ) = N2 (z, t ) = 0. Для упрощения расчета функция Ф1 (z, t) определяется из условия равенства нулю суммарного значения тока смещения на h цилиндрической поверхности пьезокерамической пластины J Drlr=1 dz = 0 . Для этого пред-h2 ставляем ее в виде следующего многочлена: Ф1 (z, t) = A0(z2- 2h2z + h22 ) Jq(r, t)rdr . (2.19) Данное выражение учитывает условия неразрывности деформаций ^1 = 0 и за- 5z|z=h2 земление металлической подложки ф^=h2 = 0. Постоянная A0определяется при удовлетворение условия С^Бц 5ф e323 5r |r=1 dz = 0. (2.20)
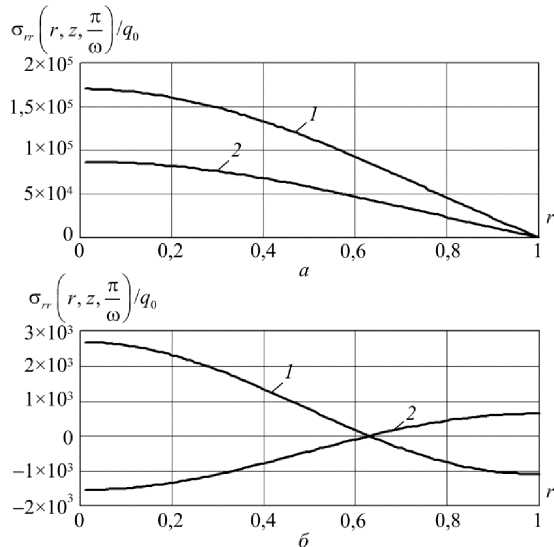
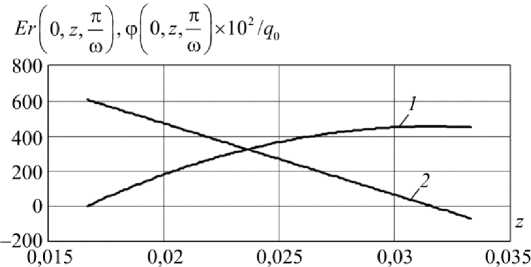
3. Численные результаты. Выводы В качестве примера рассматривается биморфная пластина, имеющая следующие физические и геометрические характеристики аксиально поляризованных пьезокерамических пластин состава ЦТС–19 [24] и металлической стальной подложки: IC(1) Г^1 Г^1) Г^1) Г^Н — Л П Q Q1 A 1 S4 ?d.lv1D10 Ы/м2p p 1 — {С11 , С зз , С12 , С13 , С 55 } {10.9, 9.1, 6.1, 5.4, 2.4jX10 H/м , {e31, езз, e15 } = {-4.9, 14.9, 10.6} Кл/м2, {£11,e33} = {7.73, 7.2б}х10-9Ф/м, p(1) = 7730 кг/м3, (2) C(2) C(2) C(2) C(2)l-f21 21 2 2 9 31хЮ10 Н/м2 { Си , С зз , С12 , С13 , С 55 } {21, 21, 2, 2, 9.3}х10 н/м , p(2) = 7800 кг/м3, h2= 0,5 х10-3 м, b = 3 х10-2м. Рассмотрим случай действия равномерно-распределенной гармонической нагрузки q (r, t ) = q (t ) = q 0 sin(ra t), где q0 - амплитудное значение интенсивности в безразмерной форме; го - относительная частота вынужденных колебаний (го = го*b^р(2) j с12, го* - круговая частота вынужденных колебаний). На рис. 2–4 изображены графики, характеризующие изменение напряженно-деформированного состояния и характер распределения электрического поля в рассматриваемой конструкции при го = 111/5 (111 - положительный параметр, соответствующий первой частоте собственных колебаний). Их анализ позволяет сделать следующие выводы. 1) При жестком закреплении конструкции на лицевой поверхности пьезокерамической пластины одновременно образуются зоны растяжения и сжатия, что приводит к появлению электрических зарядов разных знаков. Поэтому использование сплошного металлического покрытия нецелесообразно в связи с индукцией на электроде электрического потенциала небольшой величины. Для решения данной проблемы, когда частота внешнего воздействия го <1П, для регистрации разности потенциалов V (t) необходимо использовать два разрезных круговых электрода (радиус R раздела электродов определяет нулевое значение функции J0 (j1 r), R = 0,63). Подключение электродов к измерительному прибору позволяет определить V (t): R 1 V(t) = 2 |ф(r,h,t)rdr-|ф(r,h,t)rdr . I п I Рис. 2. Зависимость амплитудных значении VI — I от толщины пьезокерамической пластины h*: а - шарнирное закрепление; б - жесткое защемление Fig. 2. The dependence of the amplitude values of the thickness of the piezoceramic plate: a – securing hinge; b – hard pinching ( П 1 Рис. 3. Изменение амплитудных значений оrr I r, z,— I по радиальной к Юу координате (1-z = 0,2-z = h): а - шарнирное закрепление; б - жесткое защемление Fig. 3. The change in the peak values of the radial coordinate (1- z = 0,2- z = h ): a – securing hinge; b – hard pinching n1 (_ n1 Рис.4. Изменение амплитудных значений ф! 0,z,— I-1, EzI 0,z,— I-2, к юУ к юУ по высоте пьезокерамической пластины (шарнирное закрепление) Fig. 4. The change in amplitude values, the height of the piezoceramic plate (hinge fixing) При шарнирном закреплении пластины разность потенциалов V (t) между электро-дированными поверхностями пьезокерамических пластин (в данном случае одна плоскость заземлена) определяется равенством V (t) = 2j ф( r, h, t) rdr. 2) Для конструкции с заданной толщиной подложки можно определить оптимальную высоту пьезокерамической пластины, позволяющей наиболее эффективно преобразовать внешнее механическое воздействие в индуцируемый электрический сигнал. На рис. 2 показаны графики изменения амплитудных значений разности потенциалов V [ — | для различной толщины пьезокерамической пластины. В данном случае для металлической под- ложки толщиной h2 = 0,5 x 10 высотой И) = 0,6 x10 3 м. 3 м необходимо использовать пьезокерамическую пластину I П 1 3) Амплитудные значения электрического импульса V1 — 1 при шарнирном закреп ление пластины существенно больше, чем в случае жесткого защемления ее контура (см. рис. 2, а, б). Однако шарнирное закрепление характеризуется также большими нормальными механическими напряжениями сrr в центре пластины (см. рис. 3, а, 1-z = 0, 2- z = h). Данная особенность вводит ограничения на величину интенсивности нагрузки q0. При жестком защемлении контура пластины величина сrr значительно меньше (см. рис. 3, б) (сrr = 0 при r = R), что приводит к увеличению диапазона изменения интенсивности нагрузки q0 . I П 1 4) Амплитудное значение потенциала электрического поля ф| 0, z,— I по высоте пье-I to) зокерамической пластины при разных случаях закрепления изменяется по параболической зависимости (рис. 4, кривая 1, шарнирное закрепление), соответственно график, I П 1 описывающий изменение аксиальной компоненты вектора напряженности Ez I 0, z,— I, I to) представляет прямую линию (см. рис. 4, 2). Аналогичная картина наблюдается при анализе биморфных пластин в задачах обратного пьезоэффекта [22]. В заключение отметим, что разработанный в настоящей работе алгоритм расчета позволяет исследовать биморфные конструкции с произвольным количеством упругих и электроупругих слоев.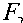
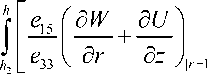
Список литературы Динамическая осесимметричная задача прямого пьезоэффекта для круглой биморфной пластины
- Piezoelectric bimorph bending sensor for shear-stress measurement in fluid flow/D. Roche, C. Richard, L. Eyraud, C. Audoly//Sensors and Actuators. -1996. -Vol. 55. -P. 157-162.
- Yoo J.H., Hong J.I., Cao W. Piezoelectric ceramic bimorph coupled to thin metal plate as cooling fan for electronic devices//Sensors and Actuators. -2000. -Vol. 79. -P. 8-12.
- Sharapov V. Piezoceramic sensors. -Springer Verlag, 2010. -498 p.
- Jurenas V., Bansevicius R., Navickaite S. Piezoelectric bimorphs for laser shutter systems: optimization of dynamic characteristics//Mechanika. -Kaunas: Technologija, 2010. -No. 5(85). -P. 44-47.
- Seung-Bok Choi, Young-Min Han. Piezoelectric actuators: control applications of smart materials. -N.-Y.: CRC Press, 2010. -280 p.
- Шарапов В., Сотула Ж. Пьезокерамические преобразователи. Новые технологи проектирования//Электроника:НТБ. -2012. -№ 5. -С. 96-102.
- Ультразвуковые колебательные системы для синтеза полимерных композиционных материалов/Д.А. Негров, Е.Н. Еремин, А.А. Новиков, Л.А. Шестель. -Омск: Изд-во Омск. гос. техн. ун-та, 2012. -128 с.
- Шикина В. Е. Расчет частоты колебаний пьезокерамического первичного преобразователя для массового расходомера жидкостей//Изв. высших учебных заведений. Поволжский регион. Технические науки. -2014. -№ 1 (29). -С. 54-63.
- Ивина Н.Ф., Тагильцев А.А. Анализ собственных колебаний дисковых изгибных пьезопреобразователей с произвольным соотношением размеров //Электронный журнал «Техническая акустика». -2005. -№ 2. -С. 1-9. -URL: http://webcenter.ru/eeaa/ejta.
- Янчевский И.В. Минимизация прогибов электроупругой биморфной пластины при импульсном нагружении//Проблемы вычислительной механики и прочности конструкций. -Харьков, 2011. -Вып. 16. -С. 303-313.
- Никофоров С.Н. Теория упругости м пластичности. -М.: Госиздат. по арх. и стр-ву, 1955.-284 с.
- Сеницкий Ю.Э. Исследование упругого деформирования элементов конструкций при динамических воздействиях методом конечных интегральных преобразований. -Саратов: Изд-во Сарат. ун-та,1985. -174 с.
- Mohammad Amin Rashidifar, Ali Amin Rashidifar. Vibrations Analysis of Circular Plate with Piezoelectric Actuator Using Thin Plate Theory and Bessel Function//American Journal of Engineering, Technology and Society. -2015. -No. 2(6). -P. 140-156.
- Tsaplev V., Konovalov R., Abbakumov K. Disk bimorph-type piezoelectric energy harvester//J. of Power and Energy Eng. -2015. -No. 3. -P. 63-68.
- Jafar Eskandari Jam, Mahmood Khosravi, Nader Namdaran. An exact solution of mechanical buckling for functionally graded material bimorph circular plates//Metall. Mater. Eng. -2013. -Vol. 19 (1). -P. 45-63.
- Adelman N.T., Stavsky Y. Flexural-extensional behavior piezoelectric cilcular plates//J. Acoust. Soc. Amer. -1980. -Vol. 67. -No. 3. -P. 819-822.
- Karlash V.L. Resonance Electro-Mechanic Vibration of Piezo-Ceramic Plates//Int. Appl. Mech. -2005. -Vol. 41. -No. 7. -P. 535-541.
- Ватульян А.О., Рынкова А.А. Об одной модели изгибных колебаний пьезоэлектрических биморфов с разрезными электродами и ее приложениях//Изв. РАН. МТТ. -2007. -№ 4. -С. 114-122.
- Wang Y., Xu R.Q., Ding H.J. Analytical solutions of functionally graded piezoelectric circular plates subjected to axisymmetric loads//Acta Mechanica. -2010. -Vol. 215. -Iss. 1-4. -P. 287-305.
- Шляхин Д.А. Вынужденные осесимметричные колебания пьезокерамической тонкой биморфной пластины//Изв. РАН. МТТ. -2013. -№ 2. -С. 77-85.
- Shlyakhin D.A., Kazakova O.V. Non-Stationary Flexural Fluctuations of a Round Flat Bimorph Plate with Graded-Varying Thickness//Procedia Engineering. -2014. -Vol. 91. -P. 69-74 DOI: 10.1016/j.proeng.2014.12.014
- Шляхин Д.А. Динамическая осесимметричная задача электроупругости для жестко закрепленной биморфной пластины//Вестник Пермского национального исследовательского политехнического университета. Механика. -2015. -№ 2. -С. 164-178 DOI: 10.15593/perm.mech/2015.2.11
- Shlyakhin D.A., Kazakova O.V. A dynamic axially symmetric goal and its extended solution for a fixed rigid circular multi-layer plate//Procedia Engineering. -2016. -Vol. 153. -P. 662-666. DOI information: 10.1016/j.proeng.2016.08.219
- Гринченко В.Т., Улитко А.Ф., Шульга Н.А. Механика связанных полей в элементах конструкций. -Киев: Наук. думка, 1989. -279 с.
- Партон В.З. Кудрявцев Б.А. Электроупругость пьезоэлектрических и электропроводных тел. -М.: Наука,1988. -470 с.
- Снеддон И. Преобразование Фурье. -M.: Изд-во иностр. лит., 1955. -669 c.
- Владимиров В.С. Обобщенные функции в математической физике. -М.: Наука, 1978. -318 с.
- Сеницкий Ю.Э. Многокомпонентное обобщенное конечное интегральное преобразование и его приложение к нестационарным задачам механики//Изв. вузов. Математика. -1991. -№ 4. -С. 57-63.
- Шляхин Д.А. Вынужденные осесимметричные изгибные колебания толстой круглой жестко закрепленной пластины//Вестн. Самар. гос. ун-та. Естественно-науч. серия. -2011. -№ 8 (89). -С. 142-152.
- Шляхин Д.А. Вынужденные осесимметричные изгибные колебания толстой круглой жестко закрепленной пьезокерамической пластины//Вестн. Самар. гос. ун-та. Естественно-науч. серия. -2012. -№ 6 (97). -С. 124-135.


