Динамическая устойчивость работы городского пассажирского транспорта

ДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ РАБОТЫ ГОРОДСКОГО ПАССАЖИРСКОГО ТРАНСПОРТА

Рассматривается проблема устойчивого во времени функционирования городского пассажирского транспорта. Доказана динамическая устойчивость оптимальной по Парето траектории в задаче городских пассажирских перевозок.

Авторами была построена математическая модель работы городского пассажирского транспорта (ГПТ) в виде многокритериальной оптимизационной задачи и изучены вопросы, связанные с существованием оптимальных (в смысле того или иного принципа векторной оптимизации) решений, признаками оптимальности, механизмами формирования и регулирования тарифных ставок [1-5]. Целью настоящей работы является изучение проблемы устойчивого во времени функционирования ГПТ. Смысл такой устойчивости понимается в состоятельности во времени тех принципов, которые порождают оптимальный сценарий развития городских пассажирских перевозок. Проблема динамической устойчивости возникает после того, как выбран определенный принцип оптимальности (например, принцип равновесия спроса и предложения, принцип оптимальности по Парето, принцип лексикографического предпочтения и т. д.), выявлены условия существования и построена оп тимальная (в смысле выбранного принципа) траектория. После того как проведены эти предварительные исследования и принято решение об их применении на практике, наступает этап реализации оптимального сценария в реальном времени, т. е. «движения» системы по оптимальной траектории. Если при этом в любой текущий момент, оставшийся (до конца процесса) участок траектории продолжает быть оптимальным в первоначальном смысле, то такая траектория называется динамически устойчивой. Нарушение динамической устойчивости в тот или иной момент времени (по какой-либо заранее непредусмотренной причине) приводит к невозможности реализации до конца выбранной траектории и, следовательно, к необходимости пересмотра ранее принятых планов, ценностей, соглашений.

Принцип динамической устойчивости является обобщением на сложные системы принципа реализуемости Р. Беллмана из теории оптимального управления и был впервые предложен Л. А. Петросяном [4] в теории кооперативных дифференциальных игр.

Перейдем к формализации работы ГПТ и понятию динамической устойчивости.

Предприятия ГПТ, предоставляющие услуги различных видов транспорта, характеризуются одними и теми же показателями (затраты, прибыль, штат сотрудников, подвижной состав и т. д.), а различные виды транспорта имеют одинаковые характеристики (скорость движения, вместимость, удобство перемещения пассажиров и т. д.). Не углубляясь в технические характеристики различных видов транспорта, будем считать, что троллейбус, автобус и трамвай - это один вид транспорта, с различными моделями подвижного состава. Все предприятия, занимающиеся перевозкой пассажиров, назовем транспортными предприятиями (ТП).

Для построения общей математической модели работы ГПТ введем следующую систему обозначений: А= {1,., и} - множество закрепленных за данным ТП маршрутов; i - номер маршрута; j - номер остановки на i -ом маршруте (там, где это не вызывает путаницы, индекс i будем опускать); Г - число остановок на маршруте i ; к - индекс марки транспортного средства (ТС), к=1, ..., т ; m _k - число ТС марки ку данного ТП; x i_k -тариф (цена одного билета) по маршруту i для категории пассажиров Z=1, . ., р и ТС марки к ; z j - среднее время стоянки ТС на остановке./ маршрута i (вычисляется прогнозно, const - среднее значение за год); t i - время (момент) прихода ТС на остановку j по маршруту i; y'_k - число ТС марки к, выделенных (курсирующих) по маршруту i ; P j - число всех вошедших пассажиров на остановке,/ на маршруте i (вычисляется прогнозно, т. е. const - среднее значение за год); c _k - постоянные затраты ТП (в среднем в год) на содержание одного ТС марки к ; s _k - переменные затраты ТП (в среднем в год) на эксплуатацию одного ТС марки к (ремонт, заправка и т. д.); p‘_k - почасовая зарплата одного водителя ТС марки к на маршруте i ; n k - количество водителей одного ТС для к и i за рабочий день; A _k - количество рейсов, осуществляемых за год одним ТС марки к ; ц _l - доля пассажиров категории Z от их общего числа; ф k - длительность (в часах) рабочего дня для к и i ; с - коэффициент пропорциональности стоимости недвижимости и хозрасходов ТП к количеству подвижного состава; d - количество рабочих дней в году; to - доля налоговых и страховых отчислений от годовой выручки ТП; о ² -среднеквадратическое отклонение интервала движения от графика; ^ j - вероятность отказа в посадке на остановке,/; W¹ - функция полезности пассажиров категории Z, оценивающая качество обслуживания пассажиров по маршруту; T j - средняя продолжительность ожидания посадки на остановке./ маршрута i ; T - время в пути по маршруту i ; F - функция прибыли данного ТП; V - функция, описывающая суммарный объем перевозок пассажиров в среднем в год для данного ТП.

Матрица x _l = || x l_k ||n _х m называется тарифной сеткой для данной категории Z пассажиров. Ряд x = { x _l , l = 1,К , p } называется общей тарифной сеткой. Множество всех возможных тарифных сеток для данного Z обозначим X _l , а множество всех возможных общих тарифных сетокА.

Матрица У = ^y ||_{n х} m называется распределением ТС по всем маршрутам. Множество всех возможных распределений обозначим У

Последовательность t = { t i ,К , t r } , где t j <  t ' _{+ 1} , называется графиком движения ТС по маршруту i . Вектор t = ( t ¹ ,К , t ⁿ ) называется графиком движения ТС данного ТП. Множество всех возможных графиков движения обозначим Т .

Тройку g = ( х , у , t ) будем называть управляющим параметром для ТП, если х е Х , у е У, t е Т , где

X = { x е R а| 0 <  x ik <  х^ , I = 1,К , p , i = 1,К , n , k = 1,К , m } ,

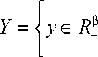
n

X y k <  m k , y k ^ 0, i = 1,K , n , k = 1,K , m I ,

T = { t е R ₊ r | t j <  t j <  t j , i = 1,K , n , j = 1,K , r i } , где a — p • n • m , в = n • m, r = r ¹ +K + r ⁿ , x [ _k - максимальная стоимость проезда по маршруту i пассажира категории Z на ТС марки к, t j , t j - минимально и максимально возможное время прихода ТС на остановку/ маршрута i . Так как «оптимальность» этих трех групп, управляю

щих параметров

( x , y , t ) = { { x , l = 1,K , p } , y , t } =

= {l| ^xlk||

n х m х p

понимается в смысле их соответствия «наилучшим» значениям выбранных критериев качества, то нас будут интересовать следующие функциональные зависимости: T = T ( y , t ) , W ¹ = W ¹ ( x , y , t ) , F = F ( x , y , t ) , V = V ( x , y , t ) .

Приведенные построения позволяют формировать математическую модель работы одного ТП в виде следу

ющей задачи многокритериальной оптимизации:

Ti ( у , t ) =

T ( y , t ) ₊ m 2 X y k k =1

m о2 IX yk

V k =1

2 T ( y , t )

+ ^j

T (У, t)

m

X yk

k =1

^ min,

j = ^1,...^,P , i = 1,...,n;

^где T ( y , t ) = X ( [ t j +1 ^- t j 1⁺ z j ) ;

j =1

W¹ ( x , У , t ) = XX a ki x ki + XX в ki y k + SZ r L Y ji t - ^ max, (2) е N k = 1             i е N k = 1            i е N j = 1

¹ = 1,..., р ;

nm

V (x, У, t ) = XX i=1 k=1

r i -1

A k X Pj j=1

pnm

F ( x , У , t ) = XXX x k l =1 i =1 k =1

y k ^ max;

r i -1

ц i A k X Pj j=1

y kⁱ

-

mn

-XI cckmk+sk X yk - k=1 V                  i=1     ?

mn

- dXX ^kpknkyk - toF+ ^ max k=1 i=1

при следующих ограничениях:

n

X y k <  m k , к -1

i =1

., m;

y k >  0, ( y k - целоечисло ) , i = ' 1, ..., п; k = 1, ..., т; (5) 0 <  х\_к <  xk , l = 1,К , p ; i = 1, ..., п; k = 1, ..., т; (6)

t j <  t j < j , j = 1, ..., P; k= 1, ..., n.          (7)

Совокупность g = ( x , y , t ) назовем допустимым управлением в задачах (1)-(7), если для них выполнены условия (5)-(7). Таким образом, множество всех допустимых управлений можно представить в виде прямого произведе-ния^ - У - Т .

Работа всего ГПТ представляет собой сложную структуру, в которой принимает участие большое количество ТП, обслуживающих все маршруты города. Поэтому если работа каждого ТП в отдельности описывается моделью вида (1)-(7), то работа всего ГПТ - совокупностью таких моделей.

Для построения математической модели работы всего городского пассажирского транспорта будем считать что:

• 1)    перевозки в городе осуществляются всего h различными транспортными (пассажирскими) предприятиями П 1, ..., П ^ ;

• 2)    в модели (1)-(7) выделены параметры, имеющие отношение к конкретным ТП (т. е. разные для разных ТП); снабдим их индексами ТП: N ^а , n ^а , т ^ , щ^а , c ^а , s ^а , F ^а , V ^а ( a =1,.,h);

• 3)    все остальные параметры модели (1)-(7) одинаковы для всех ТП.

Полученные таким образом h моделей предприятий обозначим символами Q ₁,^If.., Q h . Следовательно, математическая модель работы всего ГПТ может быть представлена совокупностью

Q = ( Q _a , a = 1,'I, h ) .               (8)

Множество всех троек (x,y, t), удовлетворяющих условиям (5)-(7) при замене N на N ^a (и соответственно, п на n ^a ) обозначим M ^a = X ^а - Y ^а - T ^а . Тогда символически модель (8) можно записать в виде _

T ( y , t ) ^ min , j = 1, ..., r ;

j               ( y, t )eY ax t a i e Na; a = 1,..., h

W ^l ( x , y , t ) ^ max , l = 1,..., p ; a = 1, ..., h ;

'      ( x , y , t ) e m ^a

V ^a ( x , y , t ) ^ max , a = 1,..., h ;

• *     ( x , y , t ) e m ^a              _

F ^a ( x , y , t ) ^ max , a = 1, ..., h .

'      ( x , y , t ) e M ^a

Первые две группы показателей T j и W ^l отражают интересы пассажиров, а вторая группа у ^а и F ^а - интересы ТП.

В случае необходимости подчеркнуть принадлежность тройки (x,y, t) предприятиюП , мы будем писать Y^a= ( x ^a , y ^а , t ^а ) Е M ^а .                  ^а

Таким образом, допустимым управлением в модели W работы всего ГПТ следует считать совокупность { y^a e M ^а , а = 1,К , h } . Множество всех таких допустимых управлений в модели Q будем обозначать через М .

Модель Q , построенная на микроуровне, представляет собой многокритериальную задачу оптимизации с числом критериев h n ^a

(2+р ) h+ц га

=1 i =1

и числом ограничений h~| h na

• 1    + ( h + p ) I n ^a m ₊ ££ r a , _                  a=1 _         a=1 i =1

где через r a - количество остановок по маршруту z, обслуживаемому предприятиемП _а . Исследование модели столь большой размерности представляется весьма трудоемким делом. Поэтому в зависимости от конкретных целей исследование практически приемлемые и полезные рекомендации можно получить путем применения различных приемов модификации исходной (общей) модели (8). Можно использовать следующие способы модификации:

• 1)    осреднение показателей:

• -    по остановкам и по маршрутам для отдельных предприятий;

• -    категориям пассажиров для определенных предприятий;

• -    количеству пассажирских предприятий для общей модели работы всего ГПТ;

• 2)    Выделение одного главного показателя:

• -    выбор одного главного критерия при исключении остальных критериев из рассмотрения;

• -    выбор одного главного критерия с присоединением условий на остальные критерии в ограничения;

• 3)    агрегирование модели работы всего ГПТ: в этом случае модель Q изначально строится не в виде совокупности (8), а как одна модель вида (1)-(7), где все параметры являются агрегированными - все маршруты города, все остановки в городе, общее количество транспортных средств в городе ит. д.;

• 4)    декомпозиция общей модели работы ГПТ по различным параметрам: по видам транспортных средств -автобусные, трамвайные, троллейбусные маршруты, государственные и частные виды транспорта (государственные и частные пассажирские предприятия) и т. д.

• 5)    Снижение уровня абстракции (формализма): в этом случае допускается укрупнение и упрощение некоторых параметров модели - рассмотрение одной марки транспортных средств ( к = 1), единого тарифа по всем маршрутам города и маркам транспортных средств ( x j. = x l ), одинаковость норм постоянных и переменных затрат, налоговых и страховых отчислений по всем пассажирским предприятиям и др.

В зависимости от содержания исследуемых конкретных вопросов, можно выбрать те или иные модификации из приведенного перечня и применить к ним соответствующие подходы из методов оптимизации, теории многокритериальных задач, теории игр и другие, а также соответствующие принципы и понятия оптимального выбора управленческого решения.

Пусть работа ГПТ рассматривается на конечном отрезке времени [0, Т|, где t = 0 - начало планового периода, т = Т- конец этого периода. Предположим, что измерения значений всех параметров задачи (1)-(7), зависящих от времени, а также корректировка управляющих воздействий ( x , y , t ) осуществляется в дискретные моменты вре-мениt = 0,1,..., Т- 1, Т.

Динамический аналог модели (8) обозначим символом

q[0-T1= [Qa0,T], a = 1, ..., h], где Q[0'т1 - динамическая модель транспортного предприятия с номером а, в которой показатели (2)-(4) принимают «интегральный» вид

TTT

W^l = f W T , V = f V , F = f F t ,     (9)

т=0               т=0              т=0

где WTl, VT, F в момент т вычисляются по формулам (2)-(4). Показатель (1) в динамической модели не рассмат ривается, так как не имеет «интегрального» аналога.

Дальнейшие построения будем приводить для одного произвольного ТП, опуская в обозначениях индекс а (т. е. символ Q[0’т1 будет означать модель одного ТП).

Имея в виду зависимость параметров x*k, mk, tj и tj, множество допустимых управлений в задач Q[0’т] обо значим:

M ^{[ 0}’ ^{т 1}

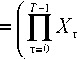
Л / т -1

^Х| П Y

^J V^T =⁰

А (т -1 А ^Х| П T T

J V ■      / где Xт, YT, Тт в каждый момент t описываются условиями (5)-(7). Примем также обозначения Y(•) = (Y0 ’ Y1 ’’■■■ ’ Yт-1), где Yt = (xт, Ут, tт), т-0,1, ., Т-1.

Пусть в задаче Q^{[ 0}’ ^{т 1} выбран конкретный принцип оптимальности (п.о.), который обозначим символом G, а G(0, Т ) с M ^{[ 0}’ ^{т 1} - множество допустимых управлений, удовлетворяющих этому п.о. Каждый элемент y ( ^ ) OG(0, Т) по определению порождает оптимальные (в смысле п.о. G) значения всех показателей (9). Поэтому Y ( • ) мы будем называть оптимальной траекторией (или оптимальным сценарием) развития ТП.

Для определения динамической устойчивости оптимальной траектории введем следующие обозначения: ^Y( ")| , _t . T 1 - сужение траектории Y ( ^ ) на отрезке времени [t, Т|, t - 0,1,..., Т- 1; G(t, Т ) - аналог множества G(0, Т ) в текущей задаче Q^[t ’ ^{т 1} , определенной на траектории y ( ^ ) , отличающейся от Q^{[ 0}’ ^{т 1} лишь продолжительностью.

Определение. Траекторию Y (•) OG(0, Т) назовем динамически устойчивой (д.у.) в модели Q[0’т 1, если выпол нены следующие условия:

1)G(t,7) ^Ф ,t-0,1,.,Т-1;

2) ^Y(" )I [_T ’ _т 1 е G(t, Т) для всех т -0,1, .,Т-1.

Множество оптимальных траекторий G(0, Т ) называется д.у в модели Q^{[ 0}’ ^{т 1} , если д.у. все его траектории.

Одним из наиболее распространенных п.о. в многокритериальных задачах является п.о. по Парето. Исследуем д.у. траекторий, порожденных этим п.о. в задаче Q^{[ 0}’ ^{т 1} .

Итак, пусть в Q[0’т в качестве п.о. G выбран п.о. Паре то (обозначим через Gp )0 т 1

Траектория ^Y ( " ) ^e M ’ называется оптимальной по Парето в задаче Q^{[ 0}’ ^{т 1} , если не существует такой допустимой траектории y ( " )^g M ^{[ 0}’ ^{т 1} , при которой

W ^l ( y ( " ) ) > W ^l ( y ( " ) ) ’ l = 1’K ’ p ;

V(y("))>V(y("))’ F(y("))>F(y(")), причем хотя бы одно из этих^ + 2 неравенств строгое.

Множество оптимальных по Парето траекторий в задаче Q^{[ 0}’ ^{т 1} обозначим G ^p ( 0. т ) .

Так как множество M[0’т 1 компактно (см. (5)-(7)), а функции (2)-(4) непрерывны на M[0’т 1, то по теореме 7.6 [5. С. 185] Gp (0,т) ^ф. Аналогичным образом можно доказать непустоту множеств Парето G(t, Т) во всех теку щих задачах Q[t’т 1 ,t - 1, ..., Т- 1, определенных вдоль Парето-оптимальной траектории y(") ■

Рассмотрим произвольную траекторию

Y ( " ) e G ^p ( 0, т ) .                 (10)

Предположим, что траектория (10) динамически неустойчива, т. е. существует такой момент т'е ( 0, т ) , при котором

Y ( " ) [ T‘, т 1 ^й G p (т' ’^т ) .

Тогда найдется такое Ре G ^p ( т' , т ) , что выполнены одновременно^ + 2 строгих неравенства:

f w (e^fxpoi^ 1 ). ^l = v". p ;

т=т'             т=т'

Ь'ттоффои; т=т'            т=т'

^от^тои)- т=т'            т=т'

Для любого из / первых_р неравенств имеем:

f W w+ e W («■Uibf^oU+ f w ^l (you,] т=т'             т= 0                             т=т'                        т= 0

(так как прибавляемая к обеим частям величина неотрицательна). Построим совокупность

(V(")l[0^11’₽), которая, очевидно, является допустимым управлением в задаче Q[0’т 1, т. е. принадлежит M[0’т 1. Последнее неравенство теперь можно переписать так:

W^l (М, - . ) ’ в ) = f W T ^l (Y C) [ 0, t.- 1 1 ’ в ) >  2 Х ( Y ( " ) ) = W^l ( У0) . т= 0                             t= 0

Это неравенство противоречит (10).

Таким образом, мы показали, что в задаче Q^{[ 0, т 1} оптимальная по Парето траектория существует и динамически устойчива. Ввиду произвольности y ( ) из выражения (10) это же утверждение верно для всего Парето-оптимального множества G ^p ( 0, т ) .

В работе построена динамическая модель работы транспортного предприятия. Рассмотрена проблема устойчивого во времени функционирования городского пассажирского транспорта. Доказано существование оптимальной по Парето траектории в построенной динамической задаче. Применен принцип динамической устойчивости, который может рассматриваться как механизм реализуемости (состоятельности во времени) решения системы вдоль оптимальной траектории. С помощью этого принципа доказана динамическая устойчивость оптимальной по Парето траектории в задаче городских пассажирских перевозок.