Динамическая визуализация решения дифференциальных уравнений при преподавании высшей математики

В связи с изменением учебных планов и сокращением часов, отведенных на изучение высшей математики, необходимо внедренияеновых методов обучения, которые позволят за достаточно короткий промежуток времени обеспечить высокий уровень овладения изучаемым материалом и закрепления его на практике. Поэтому методические инновации связаны с применением информационных технологий обучения.

Применение информационных технологий на занятиях по высшей математике предоставляет перспективные возможности для обучения: позволяет сделать аудиторные занятия более интересными, динамичными, визуализированными.

В статье рассматривается применение информационных технологий, а именно математическое моделирование, для изучения темы «Дифференциальные уравнения».

Математическое моделирование является основой научного познания окружающего мира. Суть математического моделирования заключается в перенесении реальных свойств объекта или процесса на некоторые математические отношения на конкретной базе, состоящей из декартовых произведений изученных в математике множеств, имеющих определенную математическую структуру. Физические, химические, биологические и социальные процессы не являются в этом смысле исключением. Одним из распространенных способов изучения явлений математическими методами является моделирование этих явлений и процессов дифференциальными уравнениями и их системами. Простейшие модели явлений и процессов описываются обыкновенными дифференциальными уравнениями и даже более узким их классом – обыкновенными линейными дифференциальными уравнениями. Можно сказать, что линейные дифференциальные уравнения и их системы являются достаточно адекватной математической моделью процессов, либо слабо нарушающих состояние системы, в которой они протекают, либо протекающих в течение малого по сравнению с характерным временным масштабом системы. При учете влияния процессов на систему, либо при изучении их долговременного поведения математическая модель линейных дифференциальных уравнений становится непригодной и ее необходимо заменить на нелинейную модель. В этой статье мы рассмотрим линейные процессы. Именно линейные дифференциальные уравнения хорошо изучены, так что их решение обычно легко алгоритмизируется, поэтому именно эти уравнения и изучаются в стандартных курсах дифференциальных уравнений. Однако даже основы теории обыкновенных линейных дифференциальных уравнений плохо усваиваются студентами нематематических факультетов. Причинами этого, по-видимому, являются некоторая абстрактность материала и малая степень наглядности. Как неоднократно отмечалось в работах [1] – [5], графическая визуализация излагаемого материала с помощью системы компьютерной математики (СКМ) Maple и особенно динамическая визуализация помогает качественному усвоению абстрактного материала, а также более глубокому пониманию изучаемых объектов и явлений. Следует также отметить, что для неспециалистов в математике гораздо более важным является аспект математической формулировки модели и ее исследование, чем тонкости, связанные с теорией дифференциальных уравнений. Поэтому при изложении темы дифференциальных уравнений для студентов необходимо максимально упростить процедуру ввода задачи Коши, перенося акцент на исследование решений и выяснение их смысла.

Рассмотрим программные процедуры автоматизированного решения дифференциальных уравнений и различные способы динамической визуализации с помощью системы компьютерной математики Maple.

СКМ Maple позволяет находить в квадратурах общее решение систем обыкновенных линейных дифференциальных уравнений с помощью стандартной команды dsolve(Eqs,Vars), где Eqs – система обыкновенных дифференциальных уравнений (ОДУ), записанных в виде неупорядоченного множества {Eq1,Eq2,…,Eqn}, Vars – неупорядоченное множество искомых функций {y1(x),y2(x),…, yn(x)} (см., например, [6]).При этом решение выдается в виде неупорядоченного множества равенств:

{y1(x)=F1(x,_C1,..,_Cn), y2(x) = F2(x,_C1,..,_Cn), ..,yn(x)= Fn(x,_C1,..,_Cn)}, (1) в которых Fi(x,_C1,..,_Cn) – функции переменного x и n произвольных констант _Ci; при этом функции Fi могут выражаться через элементарные или специальные функции, либо в тех случаях, когда программе не удается найти явное значение интегралов, записываться в виде квадратур. Решение же задачи Коши достигается в пакете Maple этой же командой в формате dsolve({Eqs,IC},Vars), где IC – начальные условия. В этом случае решение выдается в явном виде:

^{ У 1 ( x ) = F 1 ( x ), y 2 ( x ) = F 2 ( x ), .., У п ( x ) = F n ( x )} . ⁽²⁾

Формат вывода решений (1) – (2) не позволяет непосредственно использовать полученные решения для их анализа и построения графиков. Для вывода решения в удобной для использования форме необходимо представить полученные решения в списочном формате векторной функции заданного аргумента. Программные процедуры GenDifSolve и DsolveCoush созданной нами библиотеки программных процедур ODES позволяют решить эту проблему и тем самым предоставляют пользователю возможность обращаться с решениями ОДУ, как с обычными функциями. Программная процедура GenDifSolve(Eq,x,y,n,G) [3] находит общее решение обыкновенного дифференциального уравнения Eq произвольного порядка n относительно функции у(х) с приданием n произвольным константам имен Gi:

Следует прокомментировать эту программную процедуру. Формат вывода произвольных констант в СКМ Maple имеет вид: _C1, _C2, …, _Cn, что не соответствует Российским математическим стандартам. В связи с этим программная процедура переводит формат вывода Maple в Российский стандарт. Приведем пример нахождения общего решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами y " - 0.2 y' + 10 y = 74sin3 х .

>Z:=(x,S)->ODES[GenDifSolve](diff(y(x),x$2)-0.2*diff(y(x),x)+10*y(x)-74*sin(3*x)=0,x,y,2,S);

>Z(x,F);

(1 x 0 ) 7 3/111 x )      ( x )    ( 3/ПТ x )     555          925

e    sinl---—--- I F + e cosl---—--- I F + —cos(3 x ) + — sin(3 x )

0      10     )  ²              0      10     )  1 17                1/

В этом решении F1 и F2   – произвольные константы согласно обозначениям пользователя. Для получения частного решения данного уравнения, отвечающего значениям констант F1=1, F2 =2, достаточно использовать эту же команду в следующем формате:

>Z1:=(x)->ODES[GenDifSolve](diff(y(x),x$2)-0.2*diff(y(x),x)+10*y(x)-74*sin(3*x)=0,x,y,2,[1,2,3]);

>Z1(x);

, (1 x 0 ) . ( 3 ЛТТ x ) , „ (I x 0 )     ( 3ЛЙ x ) , 925 . _ . , 555    _ .

6 e      sinl----—---- I + 3 e      cosl ----—---- I + -p^-sin(3 x ) + -p^-cos(3 x )

Для адекватного представления компьютерных моделей объектов, описываемых ОДУ, необходимо создать программные процедуры управляемой, оснащенной динамической визуализации. Для повышения наглядности компьютерных моделей ОДУ можно использовать различный графический формат вывода решений: динамическая визуализация решения в виде графика функции с временной разверткой по переменной x, динамическая визуализация в формате динамической гистограммы и динамической цветовой/бело-серой визуализации. В случае цветовой визуализации каждому цвету (или освещенности) сопоставляется значение функции y (x).

Программная процедура AnimF(f,x,a,b,i) [3] позволяет решить проблему визуализации решения дифференциального уравнения и представить это решение в виде графика функции. В этой процедуре f -решение дифференциального уравнения, x – переменная, a, b – начало конец отрезка анимации, i – число кадров.

Рассмотрим пример решения дифференциального уравнения у ² - 0,2 y ' + 10 y - 74sin3 x = 0 с начальными условиями y (0) = 6, y '(0) = 3 в виде анимации фазовой траектории функции (рис. 1):

> ODES[AnimF]((Z1(x)),t,0,20,64):

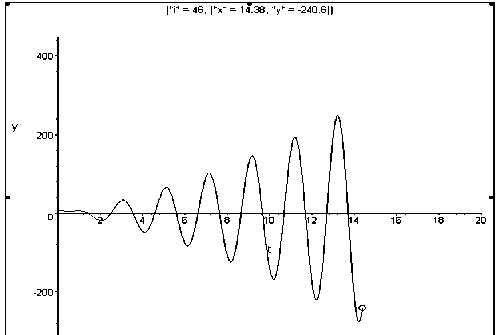
Рис. 1. Вывод решения неоднородного дифференциального уравнения с постоянными коэффициентами в виде анимации функции

Программная процедура RectangleColor(f,x,k,a,N) [3] выводит решение дифференциального уравнения в форме гистограммы. В данной процедуре f - решение дифференциального уравнения, x – переменная, a – интервал отрезка анимации, N – число кадров.

Для большей наглядности динамическая визуализация RectangleColor(f,x,k,a,N) [3] решения дифференциального уравнения в форме гистограммы может быть реализовано в сочетании с анимацией цветом. При такой реализации оттенкам серых цветов соответствуют меньшие значения функции, а темных – большие значения.

На рис.2 - рис.3 представлена графическая интерпретация решения данного дифференциального уравнения.

> ODES[DsolveCoush](diff(y(x),x$2)-0.2*diff(y(x),x)+10*y(x)-

74*sin(3*x)=0,[y(0)=3,D(y)(0)=3],y,x,[0,1.4],50);

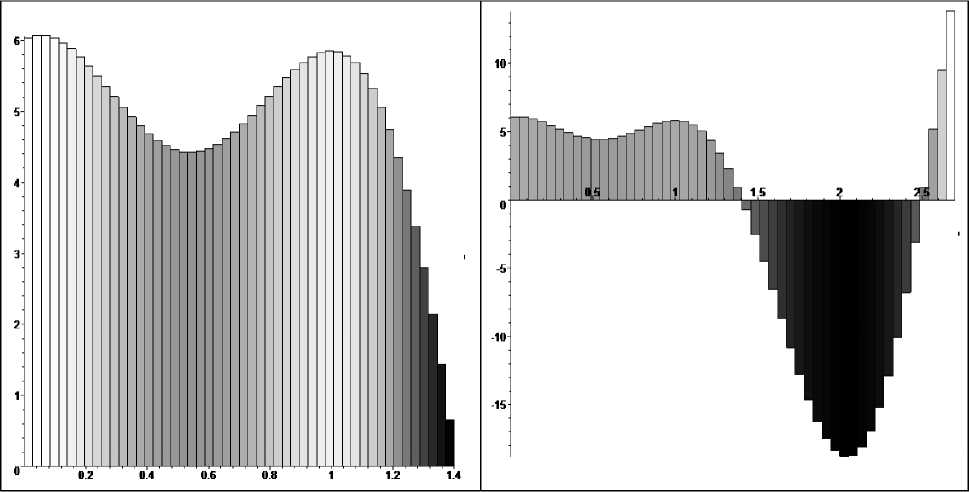
Рис. 2. Вывод решения неоднородного дифференциального уравнения с постоянными коэффициентами в виде динамической гистограммы изменения цвета. Справа иллюстрация на интервале [0, 2,28], а с лева на интервале [0, 1,4].

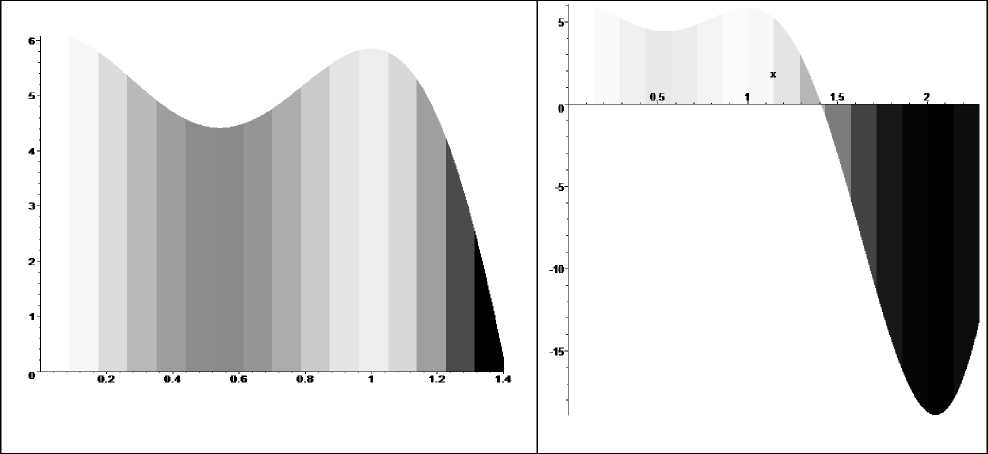
Рис 3. Вывод решения неоднородного дифференциального уравнения с постоянными коэффициентами в виде динамической гистограммы изменения цвета (гладкий рисунок). Справа иллюстрация на интервале [0, 2,28], а с лева на интервале [0, 1,4].

Таким образом, различные способы динамической визуализации с помощью системы компьютерной математики Maple позволяют наглядно представить решения дифференциальных уравнений, а, следовательно, эффективнее усвоить данный раздел высшей математики.

ЛИТЕРАТУРА:   1. Сачкова О.А. Динамические модели дифференциальных уравнений в учебном процессе // Системы компьютерной математики и их приложения:  материалы ХIII международной научной конференции.- Смоленск: Изд-во СмолГУ, 2012. – Вып. 12. -256с., с. 47- 49. 2. Сачкова О.А. Программные процедуры автоматизированного решения обыкновенных линейных и нелинейных дифференциальных уравнений и оснащенной динамической визуализации их решений. // Труды Российской школы «Математическое и компьютерное моделирование фундаментальных объектов и явлений» и Международного научного семинара «Нелинейные поля в теории гравитации и космологии» 21-26 октября 2013, -Казань: Отечество, 2013г. – с.131-132.    3.Сачкова О.А. Методическое обеспечение темы

«Дифференциальные уравнения» на основе технологии оснащенной динамической визуализации решений обыкновенных дифференциальных уравнений в системе компьютерной математики Maple // Информационные технологии в образовании и науке. Материалы международной научнопрактической конференции ИТОН-2012 8-12 октября. Изд-во КФУ, 2012.242с.,   с.159-161.   4.Сачкова   О.А. Программные процедуры автоматизированного     решения     обыкновенных     нелинейных дифференциальных уравнений и оснащенной динамической визуализации их решений // Труды Математического центра имени Н. И. Лобачевского: Материалы двенадцатой молодежной научной школы конференции «Лобачевские чтения - 2013» 24-29 октября 2013, -Казань: Казан. Ун-т, 2013. –Т.47. – с.157-160. 5.Оснащенная динамическая визуализация решений однородных линейных и нелинейных дифференциальных уравнений //  13-15 ноября 2013 года 2-й Международная молодежная научно-практическая конференция «ПОКОЛЕНИЕ БУДУЩЕГО – 2013: взгляд молодых ученых» (МЛ-03), Курск 2013, том-5, с. 326-328. 6. Дьяконов В.П., Maple 9.5/10 в математике, физике и образовании – М.: СОЛОН-Пресс, 2006.

ДИНАМИЧЕСКАЯ ВИЗУАЛИЗАЦИЯ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРИ ПРЕПОДАВАНИИ ВЫСШЕЙ МАТЕМАТИКИ

Сачкова О.А.

Резюме

Описаны основные принципы математического моделирования и программные процедуры в системе компьютерной математики Maple, оснащенной динамической  визуализацией  решений обыкновенных линейных дифференциальных уравнений.

DYNAMIC VISUALIZATION OF SOLUTIONS OF DIFFERENTIAL EQUATIONS IN THE COURSE OF HIGHER MATHEMATICS

Sachkova O.A.