Динамические особенности подвески с возможностями регулирования межкоординатных связей

Во многих областях современной техники часто возникают колебательные движения различных механических систем. Вследствие вибраций увеличиваются динамические нагрузки в элементах конструкций, которые приводят к появлению сбоев в работе аппаратуры, возникновению трещин в конструкциях и других дефектов. В связи с этим имеет особое значение создание специальных устройств, снижающих динамические нагрузки, а также меняющие свои свойства в зависимости от условий внешнего окружения [1, 2].

Известные конструктивные решения, например [3, 4], при хорошем наборе полезных свойств не всегда обладают в достаточной мере возможностями регулирования параметров, необходимыми для обеспечения эффективной работы транспортных подвесок.

Постановка задачи исследования. Общие положения

Рассматривается математическая модель устройства, которое содержит две пружины, разнесенные по сторонам причем нижними концами они опираются на основание, а верхними концами соединены с объектом защиты. Пружины вставлены таким образом, что штоки опираются нижними концами на колеса, а верхними концами соединены с поршнями, находящимися в цилиндрах, которые расположены в полой полости объекта защиты и имеют возможность двигаться под действием сжатого воздуха.

На рисунке 1 показан объект защиты 1, пружины – 2, 3, соединительная пневматическая пружина – 4, поршни (рабочая полость) – 5, 6, основание – 7, компрессор – 8, ресивер – 9, дроссель – 10, регулятор – 11, датчики давления – 12.

В рассматриваемом устройстве объект защиты 1 имеет две степени свободы движения; колебания основания 7 передаются объекту защиты 1 через обычные пружины 2, 3, пневматическую пружину – 4 и через поршни-толкатели – 5, 6, что, в свою очередь, вызывает соответствующее перемещения поршней и их взаимодействие через пневматическую соединяющую пружину 4. Работа осуществляется следующим образом: при возмущении со стороны основания 7 объект защиты 1

приходит в движение, определяемое координатами y ₁ и y ₂ , действием пружин 2, 3 и штоков 5, 6. Взаимодействие между парциальными системами возникает из-за того, что в системе существуют инерционные и упругие перекрестные связи. Движение по одной координате обязательно приводит к движению по другой координате. Необходимые изменения динамического состояния достигаются тем, что в виброзащитной системе объекта имеется пневматическая соединительная пружина 4 с жесткостью k ₃ , которая может регулироваться во время действия внешних нагрузок. Для измерения параметров динамического состояния имеются датчики 12, которые передают информацию в блок 11. Насос (или компрессор) 8 в соответствии с сигналом из блока 11 начинает работать и изменяет давление в ресивере 9.

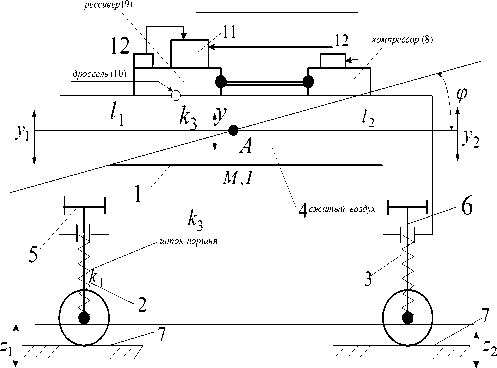
Рис. 1. Принципиальная схема динамического гасителя колебаний

Система сжатого воздуха включает компрессор, ресивер, дроссель и трубопровод для подвода воздуха к полой части объекта защиты. Динамическое гашение по координатам y ₁ и y ₂ на двух частотах определяется из соотношений:

по координате y ₁ :

2   ^ki ^k 2 + ^k 3^{( k} i + ^k 2 ) . k 1 ( Mb² + Ic² ) + k 2 ( Ic² — Mab )

по координате y ₂ :

2_        к 2 ^ki + k з⁽ k i + k 2 )

^ 2 =                                ^.

k_i ( Ic ² — Mab ) + к ₂ ( Ma ² + Ic ²)

Динамическое гашение и развязка колебаний на 3-й частоте определяется по формуле: k ® 3 = —, 3----,

( Ic ² — Mab )

где tti, ^2 - частоты динамического гашения по координатам yi и у2; (У3 — частота, на которой осуществляется развязка взаимовлияния движений по координатам yi и у2; M, I — масса и момент инерции объекта защиты; ki и к2 - упругие элементы внешнего подвеса; к3 — приведенная жесткость воздуха в рабочей полости, которая зависит от давления, создаваемого насосом или l компрессором; a = 2 , ь = —1—, c _отношения расстояний между центром тяжести и li + l 2        li +12        li +12

точками крепления упругих элементов k ₁ и k ₂ .

В свою очередь, изменение давления в рабочей полости приводит к изменению параметров, определяющих значения частот для режимов динамического гашения (формулы (1), (2) или частоты режимов развязки колебательных систем, при котором движение по одной координате не вы- зывает движение по другой. Дроссель 10 используется для предварительной настройки быстродействия системы.

Математическая модель системы

Рассматриваемая виброзащитная система обеспечивает комплекс режима динамического гашения и развязки колебаний, для которых определяются частоты динамического гашения механической колебательной системы развязки колебаний. Движение данной системы при кинематическом возмущении определяется дифференциальными уравнениями:

У 1⁽ Ma 2 + Ic 2 ) + У 1⁽ k i + k 3 ) + ^y2 ( Mab ^- Ic 2 ) - y 2 k = z i ( k 2 + k 3 ) - k 3 z 2 ;                (4)

^y 1 ( ^{Mab + Ic} 2 ) - У 1 ^к 3 ^{+ y} 2^{( Mb 2 + Ic} 2 ) ⁺ У 2^{( к} 2 ^{+ к} 3 ) = z 2^{( к} 2 ^{+ к} 3 ) - ^к 3 ^z 1 ,                (5)

где y ₁ и y ₂ – обобщенные координаты или перемещения объекта защиты;

m - масса объекта защиты;

I - момент инерции объекта защиты;

k i , к 2 - жесткости пружин, соединяющих объект защиты с основанием;

к 3 — жесткость соединительной пневматической пружины (рабочая полость);

Z 1 и z 2 — возмущения со стороны основания;

• a , b , c - коэффициенты, определяемые соотношениями расстояний от точек закрепления пружин k ₁ и k ₂ относительно центра тяжести объекта защиты.

Используя преобразования Лапласа, можно по обычным правилам построить структурную схему эквивалентной в динамическом отношении системы автоматического управления и найти передаточные функции v к1 Гк1(Mb2 + Ic2)p2 + к2 + к31-к2 Г(Mab - Ic2)p2 - к31

W 1 = У ¹ =  -------------------²—^L--------------² ,                (6)

z A ₀

• -   к 1 Г ( Mab + Ic ²) p ² - к 3 1- к 2 Г ( Ma ² - Ic ²) p ² + к + к 3 1

W ₂ = y ² =                     J^---------------------² ,                     (7)

z A ₀

где A y =Г ( Ma ² + Ic ²) p ² + к 1 + к 3 j|^ ( Mb ² + Ic ²) p ² + к ₂ + к 3 j- ( Mab - Ic ²)² p ⁴ - частотное характеристическое уравнение, из которого могут быть найдены две частоты собственных колебаний (при подстановке p = jc = , j V- 1 ); в расчете принимается, что Z 1 = z 2 = z .

Из формул (6), (7) следует, что для механической системы без трения на определенных частотах (1), (2), (3) реализуются режимы динамического гашения колебаний и развязки колебаний, а данная система может служить «фильтром вибрации» этих частот при защите объекта от внешних воздействий.

Варьируя и массоинерционными параметрами, и жесткостью пневматической пружины, можно изменять диапазоны частот динамического гашения. На рисунке 2 а, б, в показано, что частоты динамического гашения находятся в прямолинейной зависимости от величины коэффициента жесткости k ₃ , который, в физическом смысле, отражает упругие свойства воздуха в рабочей полости объекта, в свою очередь, зависящей от давления, нагнетаемого насосом или компрессором. Как следует из графиков на рисунке 2 а, 2 б, приведенная жесткость виброзащитной системы по сравнению с исходной будет возрастать, а графики зависимости при к 3 = 0 имеют значения к 1 и k ₂ , соответствующие переходным значениям упругости подвески по координатам y ₁ и y ₂ . Что касается зависимости частоты развязки колебаний по парциальным системам, то график на рисунке 2 б начинается с нулевого значения.

Настройка динамического гасителя колебаний – амортизатора может осуществляться путем предварительного выбора параметров жесткости по координатам y1 и y2, т.е. параметров k1 и k2, которые могут быть выбраны меньших значений (в 1,5 раза), чем обычно применяемых на практике; жесткость пневматической пружины k3 может быть задана в соответствии с предполагаемой внешней нагрузкой и отслеживается системой датчиков 12. Интенсивность воздухообмена, или скорость перехода системы из одного состояния в другое, может регулироваться дросселем.

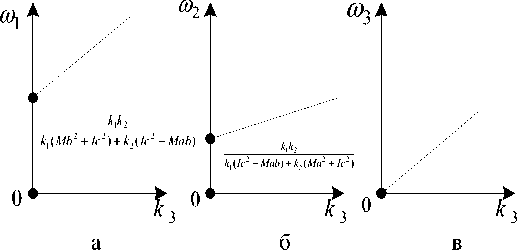
Рис. 2. Графики зависимости частот динамического гашения от жесткости пневматической пружины

Использование режимов динамического гашения колебаний в задачах виброзащиты объектов, установленных на подвижном основании, наиболее эффективно при точной настройке, когда частота внешнего воздействия совпадает с частотой антирезонанса. Динамическое гашение по координатам y ₁ и y ₂ реализуется на двух частотах, определяемых из соотношений:

2           k 1 k 2 + k ₃( k 1 + k 2 )           2  _______ k i k 2 + k 3⁽ k i + k 2) _______

^1 =     99       9      , ^2       9              9    9, k1 (Mb 2 + Ic 2) + k2 (Ic 2 - Mab)       k1 (Ic 2 - Mab) + k2 (Ma 2 + Ic 2)

а развязка колебаний реализуется на 3-й частоте, определяемой выражением:

2        k 3

.

3 =—9-----

Ic² - Mab

Заключение

Таким образом, в подвесках транспортных машин можно обеспечивать межкоординатные связи, используя нетрадиционные конструктивно-технические решения, в частности в виде регулируемых пневматических пружин. Расширение числа режимов динамического гашения в сочетании с режимами развязки колебаний позволяет создать основы для реализации более сложных форм рациональной организации динамических взаимодействий, в которых возникающие при внешних возмущениях силы инерции будут взаимно полностью или частично компенсироваться.