Динамические системы, описываемые двумя дифференциальными уравнениями с производными дробного порядка
Автор: Назаралиев Магомед-Шафи Ахмедович, Бейбалаев Ветлугин Джабраилович
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 1 т.15, 2013 года.
Бесплатный доступ
В работе рассмотрены динамические системы, описываемые двумя дифференциальными уравнениями дробного порядка. Исследованы поведения фазовых траекторий в случае действительных корней характеристического уравнения. Построены фазовые траектории при различных значениях параметра $\alpha$ и установлен переход системы из одного динамического состояния в другое при изменении параметра $\alpha$.
Динамическая система, дробная производная, фазовые траектории, фазовый портрет, характеристическое уравнение
Короткий адрес: https://sciup.org/14318408
IDR: 14318408 | УДК: 517.958
Текст научной статьи Динамические системы, описываемые двумя дифференциальными уравнениями с производными дробного порядка
Повышенный интерес к изучению нелинейных динамических систем, где реализуются идеи детерминированного хаоса и фрактальной геометрии, обусловлен тем, что закономерности таких систем становятся базовыми для установления сущности широкого круга явлений, охватывая не только физические, но и химические, геофизические, биологические, социально-экономические системы. Проникновение идей фрактальной геометрии [1] в естествознание сформировало новую концепцию — концепцию фракталов [2, 3]. Особый интерес в концепции фрактала представляет аналитический подход, основанный на использовании математического аппарата дробного интегро-дифференцирования, в рамках которого удается не только воспроизвести известные результаты, но и получить принципиально новые [4–10]. Говоря о физическом смысле дробной производной по времени, заметим, что один из критериев необратимости процессов, заключающийся в смене знака производной при изменении знака времени t → - t, в случае дробных производных состоит в замене
(—а —> t a (cos(na) + i sin(na)).
Таким образом, при переходе к дробным производным по времени часть процесса соответствует обратимым, другая часть — необратимым процессам. Такое сочетание обратимых и необратимых процессов фактически означает возможность описания нелинейных процессов путем перехода к дробным производным.
Математические методы исследования нелинейных колебательных процессов хорошо известны. Различают аналитико-топологический подход, основанный на качественной теории нелинейных дифференциальных уравнений [11–13] преимущественно для систем с малым числом степеней свободы (второго порядка), и подход, основанный на анализе асимптотических решений нелинейных дифференциальных уравнений, содержащих заданный параметр [14–16], преимущественно для систем выше второго порядка. Несмотря на значительные усилия по развитию теории нелинейных колебательных процессов, наши знания в этой области далеки от своей полноты и необходимо развитие принципиально новых подходов. В качестве одного из таких подходов предлагается метод, основанный на применении математического аппарата дробного интегро-дифференцирования.
В статье рассматриваются автономные динамические системы, отображаемые двумя дифференциальными уравнениями с производными дробного порядка:
d 0t x(t) = P (x,y), d&yCt) = Q(x,y),
где
ga _ na-1 dx(t)
d 0 t x(t) = D 0 t dt
-
— производная Капуто [8],
t
D a x(t) = — J1 [ x ( s ) dt ot v ’ Г(1 - a) dt J (t - s) a
-
— дробная производная Римана — Лиувилля [4], 0 < а 6 1.
Как известно, для математического изучения таких систем необходимо построение математического портрета рассматриваемой системы. Таким портретом является картина движения представляющей точки в фазовом пространстве, дающая взаимно однозначное отображение многообразия состояний системы, т. е. таким портретом является фазовое пространство, разбитое на траектории с указанием направления движений по траекториям.
1. Линейные однородные динамические системы, описываемые двумя дифференциальными уравнения с производными дробного порядка
Рассмотрим сначала простейшие динамические системы, принадлежащие к виду (1), а именно, те, которые отображаются системой двух линейных дифференциальных уравнений с производными дробного порядка:
d 0 t x(t) = ax + by, d ot y(t) = cx + dy,
где 0 < a 6 1, a, b, c, d — некоторые постоянные параметры. Характеристическое уравнение системы (2) имеет вид
(a — A)(d — A) — bc = 0.
Задача. Найти решение x(t),y(t) E AC 2 [0,T] системы (2), удовлетворяющее начальным условиям x (0) = x 0 , y (0) = y 0 .
Решение задачи, если корни характеристического уравнения различны, имеет вид [18]
x(t)
y(t)
X 0 (E a, 1 (A 1 t a )+ E a,1 (X 2 t a ) )
+ t a ) - MW
2 ^y 2 + (cb — ad)
2 ( ЕаД(Х 1 t a )+ E a,1 (X 2 t a ) )
+
X o c — y o a + Yy o
2 pY 2 + (cb — ad)
(Ea, 1 (A 2 t a ) - E a, 1 (A 1 t a )) ,
где X1,2 = y ± pY2 + (cb — ad) — корни характеристического уравнения (3), y = a+d• Характеристические корни λ1, λ2 являются решениями уравнения (3). Нормальная форма матрицы коэффициентов a c
и параметр α полностью определяют поведение траек- торий в окрестности особой точки. В случае, когда корни характеристического уравнения (3) действительны, действительное преобразование координат приводит систему к системе того же вида, но с матрицей коэффициентов одного из двух типов [12]:
λ 1
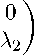
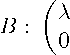
1\
λ.
В данной работе рассматриваем случаи действительных корней характеристического уравнения, т. е. случаи с матрицами коэффициентов типа A и B .
Пусть корни одного знака, а матрица типа A. В этом случае с помощью линейного однородного преобразования u = ax + ву, v = Yx + ^У система (2) приводится к виду dotu(t) = X1u, dotv(t) = X2v
где λ 1 , λ 2 — корни характеристического уравнения (3). Решение системы (5) имеет вид
u(t) = U o E a,1 (X 1 t a ),
v(t)= VoEa,1 (X2ta ), где u0 , v0 — произвольные постоянные.
Предположим, что оба корня X 1 , X 2 действительные и отрицательные. Пусть X i = — ^ i , ^ i > 0, i = 1, 2. Решение системы (5) имеет вид
u(t) = U o E a, 1 ( — M 1 t a ), v(t) = V o E a, 1 ( — ^ 2 t a ).
На рис. 1, 2 приведены графики фазовых траекторий в случае отрицательных корней характеристического уравнения. Как видно на рис. 1, фазовые траектории приближаются к началу координат при t ^ + го . Они совпадают с полуосью u, когда v o = 0, и с полуосью v, когда u o = 0. В этом случае особой точкой является устойчивый узел.
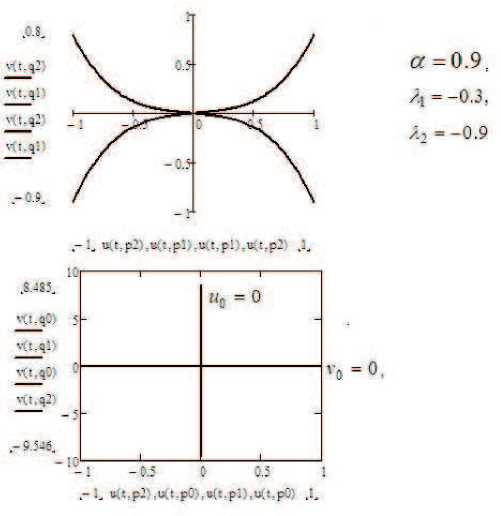
Рис. 1. Графики фазовых траекторий в случае отрицательных корней характеристического уравнения.
А когда а ^ 0 и t ^ + го , как видно на рис. 2, происходит топологическое изменение фазовой плоскости.
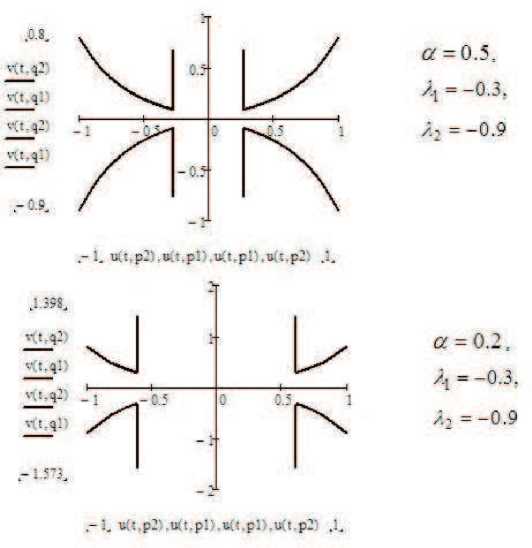
Рис. 2. Графики фазовых траекторий в случае, когда α → 0.
Пусть оба корня λ 1 , λ 2 положительны. На рис. 3 приведены графики фазовых траекторий в случае положительных корней характеристического уравнения. Как видно на рис. 3, фазовые траектории отдаляются от начала координат при t → ∞ . В этом случае особой точкой является неустойчивый узел.
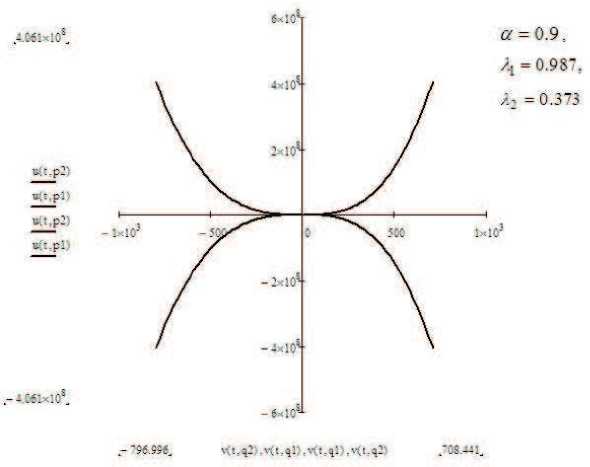
Рис. 3. Графики фазовых траекторий в случае положительных корней характеристического уравнения.
Теперь предположим, что оба корня λ 1 , λ 2 действительные, но противоположных знаков. Пусть A i = — А < 0, а А 2 = ц > 0. Тогда
u(t) = u o E a,i (—At “ ), v(t) = V 0 E a, i ( — ^t “ ).
Полуоси u, v являются траекториями, соответствующими u o = 0 и v o = 0. Если u o v o = 0, то u ^ 0, v ^ то при t ^ + то . На рис. 4 приведены графики фазовых траекторий в случае, когда оба корня λ 1 , λ 2 действительные, но противоположных знаков. В этом случае особой точкой является седло.
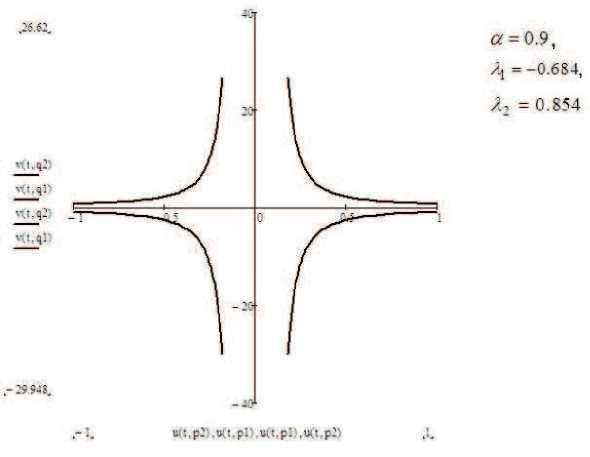
Рис. 4. Графики фазовых траекторий в случае, когда оба корня λ 1 , λ 2 действительные, но противоположных знаков.
А когда | A i | > 1, а ^ 0 и t ^ + го , как видно на рис. 5, происходит топологическое изменение фазовой плоскости, т. е. из одного состояния с особой точкой типа седло (рис. 4) переходит в другое с особой точкой типа неустойчивый узел.
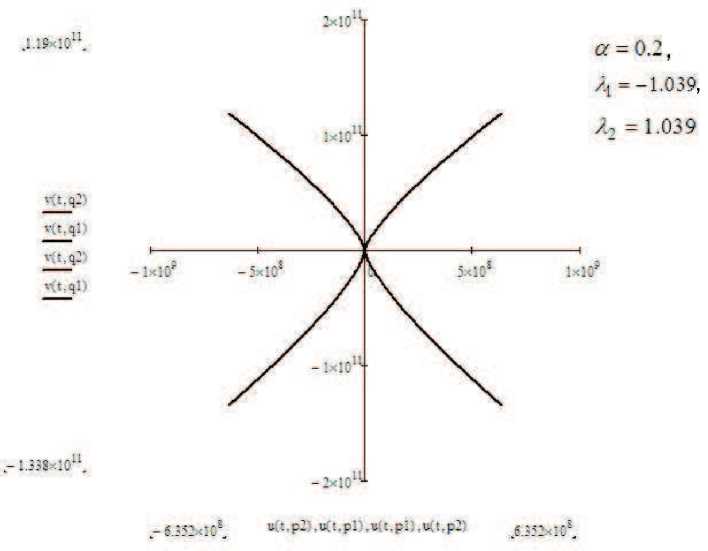
Рис. 5. Графики фазовых траекторий в случае, когда корни действительные, противоположных знаков, | λ i | > 1 и α → 0.
Рассмотрим теперь случай, когда характеристическое уравнение имеет один корень λ и этот корень действительный.
Тогда приведенная система имеет вид d0tu(t) = Au, да v(t) = u + Av.
Решением системы (6) будет
u(t) = u o E a,1 (At a ),
∞
v(t) = v o E a,1 (At “ ) + u o t a X A k t ak Е а,ак+а+1 (At “ ).
k =0
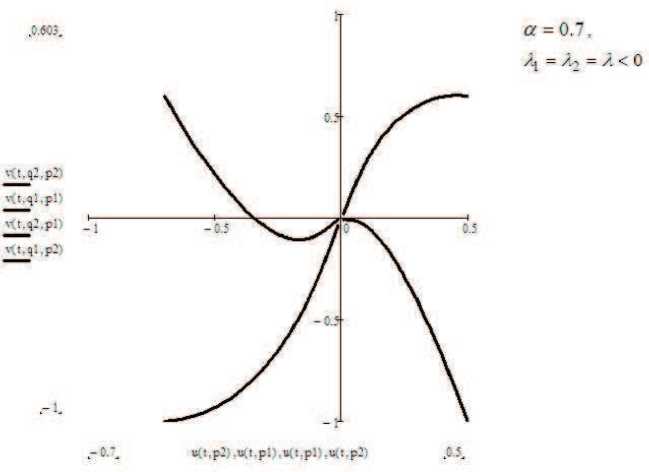
Допустим сначала, что A < 0. Как видно на рис. 6, в случае, когда u o = 0 и v o > 0, фазовые траектории представляют собой положительную полуось v, а когда v o < 0 — отрицательную полуось v.
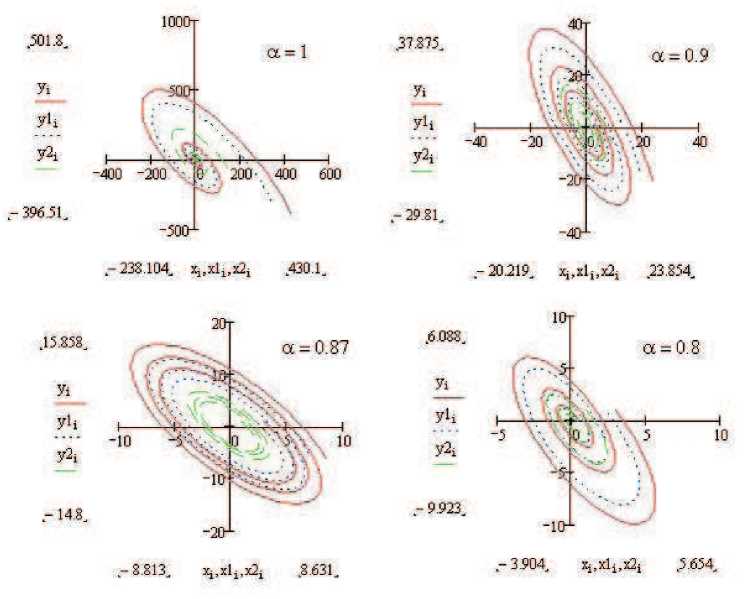
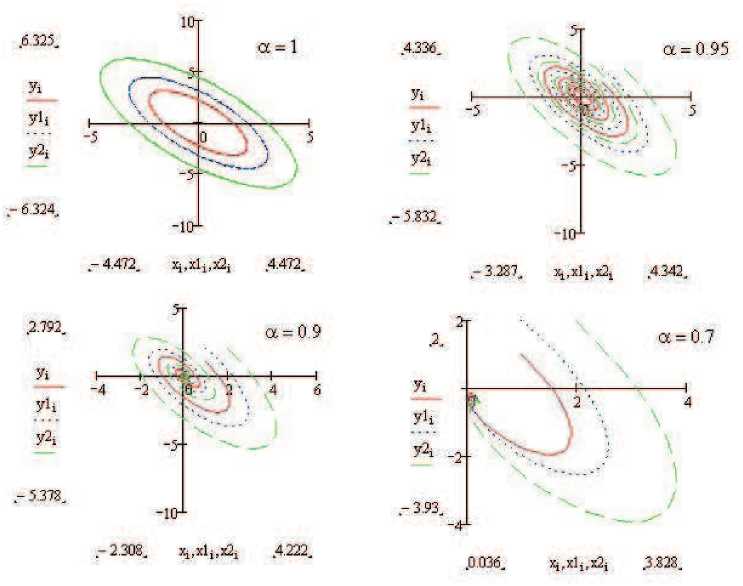
v r(t,q2,pi) Рис. 6. Графики фазовых траекторий в случае, когда характеристическое уравнение имеет один корень А < 0 и и0 = 0. v(Lq2,p2) v(t.ql,p2) В этом случае независимо от uo и vo одновременно u, v ^ 0 при t ^ +го, и особой точкой будет устойчивый узел (рис. 7). В случае А > 0 особой точкой будет неустойчивый узел. Рис. 7. Графики фазовых траекторий в случае, когда характеристическое уравнение имеет один корень А < 0. 2. Нелинейные динамические системы, описываемые двумя дифференциальными уравнениями с производными дробного порядка В работе [20] была исследована система дифференциальных уравнений с производными дробного порядка: d0atx(t) = a + x2y — (b + 1)x, 'dby(t) = bx - x2y. В случае a = 1 система (8) принимает вид dx- = a + x2y — (b + 1)x, = bx — x2y. dt Система (9) была исследована Пригожиным и Лефевром в 1965 г. [21]. Динамическую систему, описываемую с помощью системы (9), авторы назвали брюсселятором. Точка x = a, y = a, является особой точкой. С помощью замены x = x* +a, y = y* + a, ограничиваясь только слагаемыми первого порядка малости, система (8) приводится к линеаризованному виду d0atx*(t) = (b — 1) x + a2y, d0ty*(t) = -bx - a2y. Решение системы (10) имеет вид [20] x*(t) = '2 (Ea, 1 (A1 ■') + Ea,i(A2ta)) + a.- E (A11„ ) — Ea,t(A2t« )), 2 у 72 — a2 y* (t) = y0(Ect, 1 (Aita) + Ea,i (A2■' )) — (x0 +yo^b—jlr 2b (Ea, 1 (A2ta) — Ea, 1 (A11“)), 2 v72— a2 где A1,2 = —y ± 7/72— a2 — корни характеристического уравнения, y = a—2b 1). На рис. 8, 9 приведены рассчитанные по формулам (11) графики фазовых траекторий. На рис. 8 видно, что в случае b > 1 + a2при переходе к дробным производным по времени происходит переход от неустойчивого вида особой точки фазовой траектории к устойчивому виду. На рис. 9 видно, что в случае b = 1 + a2при переходе к дробным производным происходит топологическое изменение фазовой плоскости. Таким образом, учет эффектов памяти приводит к принципиально новым результатам, когда в системе возможны переходы между различными особыми точками фазовой траектории. Фазовые траектории при различных значениях а в случае b > 1 + a2. Рис. Рис. 9. Фазовые траектории при различных значениях а в случае b = 1 + a2.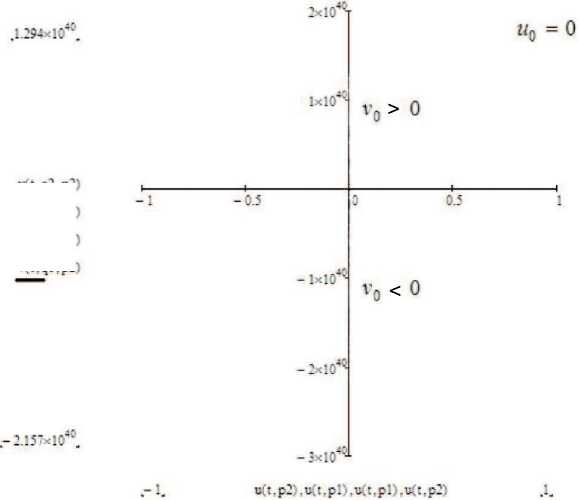
Список литературы Динамические системы, описываемые двумя дифференциальными уравнениями с производными дробного порядка
- Mandelbrot B. B. The Fractal Geometry of Nature.-New York: W. H. Freeman, 1982.-468 p.
- Олемской А. И., Флат А. Я. Использование концепции фрактала в физике конденсированной среды//Успехи физ. наук.-1993.-Т. 163, № 12.-С. 1-50.
- Зосимов В. В., Лямшев Л. М. Фракталы в волновых процессах//Успехи физ. наук.-1995.-Т. 165, № 4.-С. 361-402.
- Самко С. Г., Килбас Ф. Ф., Маричев О. И. Интегралы и производные дробного порядка и некоторые приложения.-Минск: Наука и техника, 1987.-688 с.
- Нигматулин Р. И. Дробный интеграл и его физическая интерпретация//Теорет. и мат. физика.-1992.-Т. 90, № 3.-С. 354-368.
- Чукбар К. В. Стохастический перенос и дробные производные//Журн. эксперем. и теорет. физики.-1995.-Т. 108, № 5.-С. 1875-1884.
- Мейланов Р. П., Янполов М. С. Особенности фазовой траектории фрактального осциллятора//Письма в журн. техн. физики.-2002.-Т. 28, № 1.-С. 67-73.
- Нахушев А. М. Элементы дробного исчисления и их применение.-Нальчик, 2003.-299 с.
- Нахушева В. А. Дифференциальные уравнения математических моделей нелокальных процессов.-М.: Наука, 2006.-174 с.
- Андреев А. А., Огородников Е. Н. Применение матричных интегро-дифференциальных операторов в решении задачи Коши для некоторых систем обыкновенных дифференциальных уравнений с производными дробного порядка//Тр. VI Всерос. науч. конф.-Самара, 2009.-Ч. 3.-С. 31-38.
- Бейбалаев В. Д. Решение начальной задачи для дифференциального уравнения фрактального осциллятора//Вестник СамГТУ. Сер. Физ.-мат. науки.-2009.-№ 2(19).-С. 240-242.
- Лефшец С. Геометрическая теория дифференциальных уравнений.-М.: Изд-во иностр. лит-ры, 1961.-388 с.
- Андронов А. А., Леонтович Е. А., Гордон И. И., Майер А. Г. Качественная теория динамических систем.-М.: Наука, 1966.-568 с.
- Малинецкий Г. Г., Потапов А. Б. Современные проблемы нелинейной динамики.-М.: Эдиториал УРСС, 2000.-336 с.
- Боголюбов Н. Н., Митропольский Ю. А. Асимптотические методы в теории нелинейных колебаний.-М.: Наука, 1974.-504 с.
- Хейл Дж. Колебания в нелинейных системах.-М.: Мир, 1966.-230 с.
- Моисеев Н. Н. Асимптотические методы нелинейной механики.-М.: Наука, 1981.-400 с.
- Вебер В. К. Структура общего решения системы $y^\alpha=Ay$, $0
- Назаралиев М. А., Бейбалаев В. Д. Нелинейные колебания в средах с фрактальной структурой//Сб. тр. междунар. Российско-Болгарского симпозиума "Уравнения смешанного типа и родственные проблемы анализа и информатики".-Нальчик~-Хабез, 2010.-С. 177-180.
- Назаралиев М. А., Мейланов Р. П., Бейбалаев В. Д., Шабанова М. Р. Особенности фазовой траектории фрактального "брюсселятора"//Сб. тр. VII Всерос. науч. конф. с междунар. участием "Математическое моделирование и краевые задачи".-Самара, 2010.-Ч. 3.-С. 204-210.
- Лаврова А. И., Постников Е. Б., Романовский Ю. М. Брюсселятор -абстрактная химическая реакция?//Успехи физ. наук.-2009.-Т. 179, № 12.-С. 1327-1332.


