Динамический анализ привода рычажных гидромеханизмов грузоподъёмных машин

В различных отраслях машиностроения, таких, например, как подъемно-транспортное и строительнодорожное машиностроение, а также авиационнокосмическая техника широко применяются гидроприводы, содержащие исполнительные гидроцилиндры, приводящие в действие плоские рычажные механизмы, нагруженные весовой нагрузкой. Рычажная связь и вариативность направления движения звеньев исполнительного механизма при выполнении рабочих операций обусловливают изменение весовых и инерционных нагрузок, что на этапе проектирования механизмов затрудняет реализацию имитационного математического моделирования и анализ динамики процесса их эксплуатации.

В работе [1] рассмотрен элементарный рычажный механизм с гидроприводом и приведена методика анализа его динамики, которая может быть принята за основу при проведении анализа динамики более сложных механизмов. Усовершенствованными примерами [2] таких механизмов могут служить разработанные нами гидроприводы грузоподъемного механизма [3] и рабочего оборудования фронтального погрузчика [4] (рис. 1).

Рис. 1. Кинематическая схема гидропривода рабочего оборудования одноковшового погрузчика

Обозначим постоянные и переменные параметры механизма и привода: A1 – размер установочной базы пяты гидроцилиндра О1 и шарнира стрелы О2; А2 – размер установочной базы шарнира поворота ковша О4; Х1, Х2, – координаты перемещений соответствующих секций телескопического гидроцилиндра; aj, pj - переменные углы, определяющие положение механизма. В схеме на рис. 1. совмещены два механизма, образующие соответственно кинематические треугольники О1,О2,О3 и О3,О4,О5, приводимые в движение различными секциями одного исполнительного гидроцилиндра телескопического типа, причем центральная точка О3 расположена на кулисе и ее положение будет зависеть как от подъема стрелы (при изменении Х1), так и от поворота ковша (при изменении координаты Х2).

Рассмотрим отдельно механизм подъёма стрелы (рис. 2).

Рис. 2. Кинематическая схема механизма подъема стрелы

Требуется определить функцию нагрузочного режима S 1 в зависимости от перемещения первой секции гидроцилиндра X ₁ и массы стрелы G _c без учета масс отдельных элементов гидроцилиндра, так как они совместно с переменной массой рабочей жидкости, находящейся внутри полостей гидроцилиндра, уже учтены в имитационной модели гидроцилиндра [5].

Составляя уравнение моментов относительно опоры O ₂ и приравнивая его нулю (состояние равновесия механизма), получим:

5 (xj)• sin[р, (х)-а]• Bj -

- Gc • cos{90° -[а, (X ) + у,]}• rc = 0, откуда для текущего положения механизма

⁵ ( ^X , ) =

G_c • cos { 90 ° - [a j ( X j ) + Y j ] } • r c sin ^[P j ( X ) ^-a ]• B j

Как видно из формулы (2), функция нагрузки зависит от положения механизма, задаваемого координатой X 1 и для выявления зависимости S 1 = f ( x 1 ) требуется определить функции а 1 = f(x 1 ) и р 1 = f ( x 1 ). В первом приближении данные функции можно найти на этапе проектирования механизма следующим образом. Задавая дискретно массив координат X 1 i и построив несколько положений по траекториям движения точек механизма, определяем значения а 1 i и р 1 i и аппроксимируем их математическими зависимостями, соответствующими полям парных корреляций для искомых функций.

Для нахождения более точного и универсального решения переходим к относительным параметрам, принимая в качестве линейной единицы измерения постоянный размер базы механизма A ₁ = 1.

Вводя относительные переменные B 1 = —; X. = — A 1¹ A 1

и выбирая в качестве обобщенной координаты X 1 , что равносильно перемещению поршня первой секции гидроцилиндра, так как X 1 - X = const, а, следова

i 12 ^{( Х} 1)       - ■

A 2

¹ Х 1 ■

1 - B 2

^^^^^^в

2 x 1

x2-(1 -B2) ■ (1 + B2)

^^^^^^в

2 x 1

1                      2 ■ x 1

A 22   22

J x 1 - ( 1 - B 1 ) ■ ( 1 + B 1 ) - x 1

;

Искомые функции кинематического положения механизма будут определены в результате интегрирования приведенных ниже зависимостей:

^а 1( Ч)

Р 1( _ч)

x 1max

J x1min

x 1max

=2 J

x 1min

x 1

^^^^^^в

1 - B 1 - x 1

dx ; (5)

x 1

(1- B 1) ■ (1+B 1)

dx . (6)

^^^^^^в

x 1

тельно, и X 1 = X , опишем кинематику плоского рычажного механизма, используя передаточные отношения его звеньев 1, 2, 3:

а.	= 1	d а 1
i 2( X ) = —		■ —^=^ ;
,                       • X	= Ait	dX 1
1 •			(3)
i 3,2 ( X 1 ) = 41" X 1	1 = А	d Р 1 ■ —= . dX 1

С учетом решений, приведенных в [1] для передаточных функций, имеем

Для определения нагружающего усилия S 2 рассуждения аналогичны.

Аналогичным способом, проводя разбиение механизмов на элементарные звенья, можно произвести анализ и синтез плоских рычажных механизмов любой сложности. Вычисление значений определенных интегралов (5) и (6) производится с помощью стандартной подпрограммы QART из пакета SSP прикладных программ на фортране [6].

Для применения выведенных уравнений нагрузочного режима в анализе изменения давлений в гидроприводе исполнительного гидроцилиндра используются исследования, приведенные в работе [7].

Результаты синтеза и динамического анализа, рассмотренного выше плоского рычажного механизма в CAE-системе АПМ Winmachine [8] (модуль Dynamics), приведены на рис. 3–7

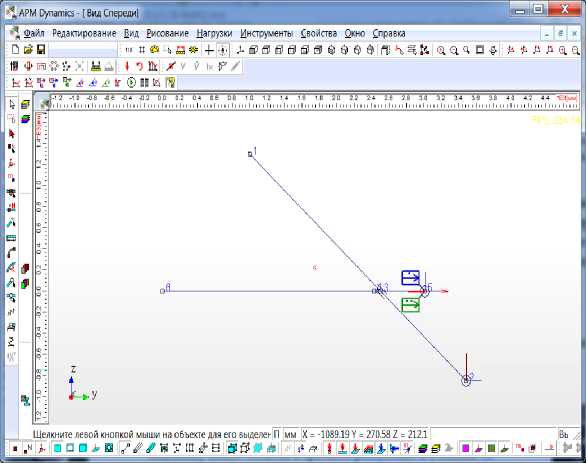
Рис. 3. Расчетная модель рабочего оборудования фронтального погрузчика

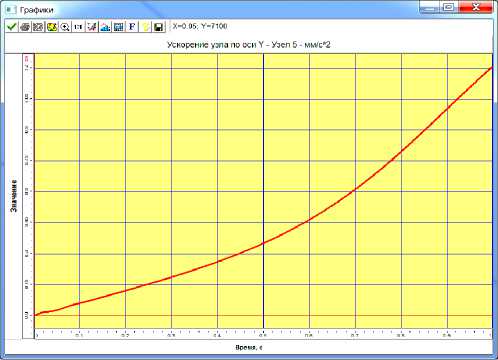
Рис. 4. Диаграмма ускорений верхнего шарнира крепления ковша

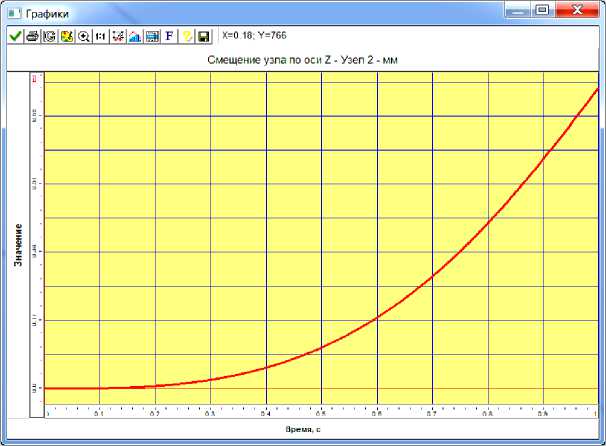
Рис. 5. Диаграмма перемещений нижнего шарнира крепления ковша

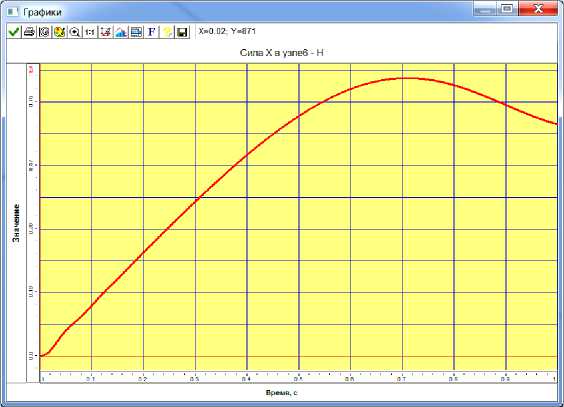
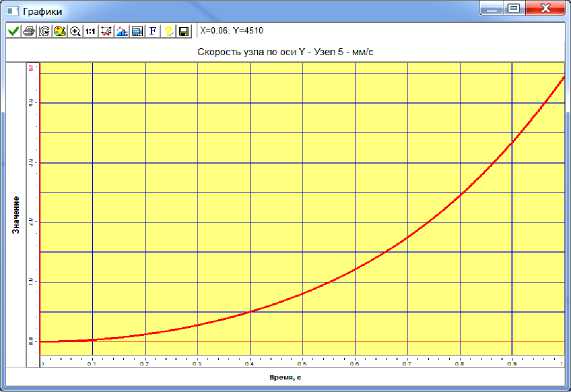
Рис. 7. Диаграмма изменения скорости подъема стрелы

Приведенная методика определения функций нагрузочного режима гидропривода грузоподъемных механизмов, использующая их относительные размеры и передаточные функции, позволяет находить переменные по рабочему ходу исполнительных гидроагрегатов функции весовых и инерционных нагрузок, действующие от элементов грузоподъемных механизмов различных типов и приводить их к элементам крепления исполнительных гидроагрегатов, что позволяет применять универсальную имитационную модель и программное обеспечение [9] без их дополнительного редактирования и последующей трансляции.

Использование пакета программ APM Winmachine кроме анализа динамических характеристик дает возможность анализировать работоспособность синтезируемых механизмов, что в совокупности с описанной методикой в итоге позволяет сократить сроки проектирования и повысить качество принимаемых проектных решений.