Динамический анализ ресурсного обеспечения предприятия в условиях кризиса

В экономике вообще и при управлении предприятиями, в частности, имеется стабильный спрос на прогнозные исследования эффективности использования ресурсов. Особенно это актуально в кризис и посткризисный период, так как неопределенность внешней среды сказывается на адекватности оценки деятельности предприятия в эти периоды.

В экономической науке широко используется концепция неоклассического понимания предприятия (фирмы) как носителя производственной функции (преобразование ресурсов в продукцию, продающуюся на свободном рынке). При управлении предприятием основной задачей становится определение соотношения объема производства и ресурсов, обеспечивающее эффективное использования ресурсов. «Организовать производство -это, значит обеспечить его факторами, соединить их в определенной комбинации, получить продукт и использовать его таким образом, чтобы сделать возможным повторение акта производства» [1, с. 76].

Производственная функция, известная в экономической теории как функция Кобба-Дугласа, позволяет исследовать объёмы производства в зависимости от двух факторов производства - численности и основных производственных фондов:

Q=A^K “ ^L ^ , (1) где Q - объем выпуска продукции, тыс. руб./год; L - численность персонала, чел.; K- объём основных производственных фондов, тыс. руб.; A -эмпирически определяемый коэффициент, обеспечивающий сопряжение размерности левой и правой части и одновременно выполняющий роль масштабного переводного множителя между всеми компонентами формулы (1); а, Р- коэффициенты эластичности выпуска продукции по соответствующему ресурсу, безразм.

В случае если хозяйственная деятельность имеет высокую материалоемкость, а выпускаемая продукция относится к наукоемкой, в производственной функции имеет смысл учесть влияние материальных ресурсов и инновационно-инвестиционных затрат на выпуск продукции:

ТС = A • 0A“ • SnA • ФОТ' • Ito5,       (2)

где ТС - общие затраты на выпуск продукции, тыс. руб./год; A - масштабный переводной множитель; 0A - оборотные активы предприятия, тыс. руб./год; SnA - внеоборотные активы предприятия, тыс. руб.; ФОТ - фонд оплаты труда (заработная плата и единый социальный налог), тыс. руб./год; Inv - инновационно-инвестиционные затраты на развитие предприятия, тыс. руб./год; а,Р,у,5 - эластичность выпуска продукции по соответствующему ресурсу, безразм. По своей величине показатели эластичности должны быть меньше 1. Выбор показателя общих затрат в качестве результирующего обусловлен желанием снизить погрешность влияния на результаты работы предприятия факторов внешней среды (величины спроса, изменения цен на рынках и пр.).

При проведении анализа на значительных интервалах времени (10-15 лет) негласно делается допущение, что технический прогресс отсутствует, и весь рост результата производства вызван изменением лишь ресурсных показателей. На самом деле результат производства может меняться из-за лучших в качественном отношении основных производственных фондов и материалов, вследствие лучшей организации труда, возрастающей стабильности кадрового состава и повышения квалификации, лучшей работы функциональных служб и обеспечивающих подразделений. Чтобы выявить подобные изменения, строится производственная функция, учитывающая технический прогресс, когда результаты производства растут во времени при неизменном количестве вовлекаемых в производство ресурсов за счет совершенствования как их качества, так и условий использования.

В зависимости от подхода к описанию технического прогресса выделяют:

• -    автономный технический прогресс по Харроду и по Хиксу;

• -    овеществленный технический прогресс по Соллоу;

• -    индуцированный технический прогресс по Эрроу и по Моисееву;

• -    подход на основе рассмотрения особого ресурса.

На их основе разработаны различные модели экономической динамики, позволяющие прогнозировать рациональное соотношение ресурсов для достижения желаемых темпов развития открытых и закрытых экономических систем, со сбалансированным и несбалансированным ростом.

Однако используемые модели имеют существенный недостаток, так как основаны на допущении сохранения пропорций между характеристиками экономических систем в течение всего ретроспективного периода (фиксированные значения), что не соответствует действительности. Иными словами, факторы являются функциями основных переменных [2, с. 59]. То есть при экстраполяции трендов различных показателей используют постоянные (фиксированные) коэффициенты, не учитывающие динамику изменения свойств как факторов производства, так и их взаимосвязей. Очевидно, что изменения условий производства, вызываемые воздействием внешней среды, вносят существенные погрешности в результаты моделирования. Кроме того, прогнозирование по модели, построенной на ретроспективной базе, переносит все «огрехи» прошлого менеджмента на перспективу.

Для анализа деятельности предприятия в условиях кризиса технический прогресс не учитывался, так как его влияние в краткосрочном периоде существенно ниже разброса уровня воздействия факторов производства.

В качестве исходной информации для анализа использованы данные результатов деятельности типичного промышленного предприятия Челябинской области за 2,5 года (14 периодов (кварталов)). Полученные исходные данные генеральной совокупности (population), «очищенные» от изменений вызванных результатами неосновной деятельности, инфляционной составляющей, приведенные к

Таблица 1

Генеральная совокупность, тыс. руб./год

№	Объем пр-ва ТСi	Об. акт. ОА i	Внеоб. акт. ВnАi	ФОТ FОТ i	Инвестиц. Invi
1	77 639	221 392	274 059	4 601	32 653
2	89 260	281 120	274 376	5 306	83 702
3	107 533	316 618	275 771	6 378	61 738
4	111 874	329 161	327 071	6 659	93 753
5	98 098	349 534	325 421	5 802	48 267
6	126 874	331 969	332 853	7 521	19 276
7	136 869	336 811	333 930	8 111	35 191
8	142 831	348 084	330 310	8 454	37 431
9	124 543	356 631	333 866	7 396	41 563
10	182 242	367 117	335 166	10 804	41 093
11	133 059	354 734	334 095	7 855	15 837
12	168 265	339 604	342 630	9 532	22 885
13	157 580	324 830	348 963	8 869	21 056
14	185 710	372 070	306 426	10 422	29 175

постоянным ценам, представлены в табл. 1.

Для анализа параметров динамики факторов производства разобьем генеральную совокупность, представленную в табл. 1, на 6 групп методом «скользящего окна». Из первоначальной совокупности выделяем 9 наблюдений с № 1 по № 9, и включаем их в первую выборку (окно). В табл. 1 данные наблюдения выборки 1 выделены жирной рамкой. Во вторую выборку включаем наблюдения из генеральной совокупности с номера № 2 по № 10. Аналогичным образом формируем остальные выборки 3, 4, 5, 6. В последнюю, шестую выборку, соответственно входят наблюдения с № 6 по № 14. Обоснование количества наблюдений в каждой выборке оставляем за рамками исследования.

Путем логарифмирования совокупности данных, каждой выборки (окна с 1 по 6), приводим их к линейному виду. Полученные системы линейных уравнений решаем методом наименьших квадратов (МНК, SSD). Расчет параметров производился программой Microsoft Office Excel 2007, инструмент Данные / Анализ данных /Регрессия, и Данные /Анализ данных /корреляция :

Е ln TCt = Е ln А + a • Е ln 0А; + ^ • Eln5nA; + у • ElnFOTj + 5 • Eln^nv;.     (3)

На основе полученных линейных уравнений рассчитаны параметры производственных функций, которые сведены в табл. 2 и 3 и представлены на рис. 1 и 2.

Практический интерес с позиции менеджмента представляет не столько исследование факторов производства, сколько анализ изменения тренда факторов производства. Объясняется это тем, что воздействуя на доминантные факторы производства, можно изменять технологию для улучшения результатов производства.

По найденным в процессе решения уравнений (3) коэффициентам регрессии (α, β, γ, δ) (см. табл. 3) и исходным данным факторов производства (А, OA, BnA, FOT, Inv) (см. табл. 1) получим расчетные значения затрат на производство (TCt) по каждой выборке,    полученные результаты представлены на рис. 3 и в табл. 4. Можно отметить высокую степень совмещения расчетных значений затрат TCt, для различных групп (линии 1–6) и фактических значений (линия – факт), рис. 3.

Динамика коэффициентов корреляции между TС ; И факторами производства, приведенные в табл. 2 и рис. 1, позволяют сделать

Таблица 2

Динамика показателей корреляции

Наименование фактора	Номер выборки
	1	2	3	4	5	6
Ln OA	0,809	0,725	0,584	0,354	0,017	0,400
Ln BnA	0,784	0,649	0,465	0,801	0,685	–0,267
Ln FOT	1,000	1,000	1,000	0,997	0,994	0,990
Ln Inv	–0,316	–0,534	–0,354	–0,363	–0,237	0,155

1,500

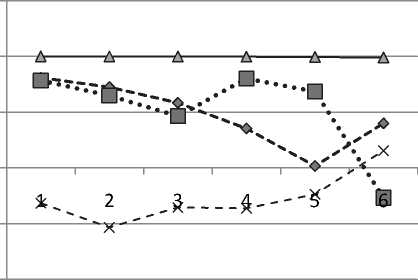
Рис. 1. Динамика показателей корреляции

LnOA

LnBnA

LnFOT

LnInv

1,000

0,500

0,000

-0,500

-1,000

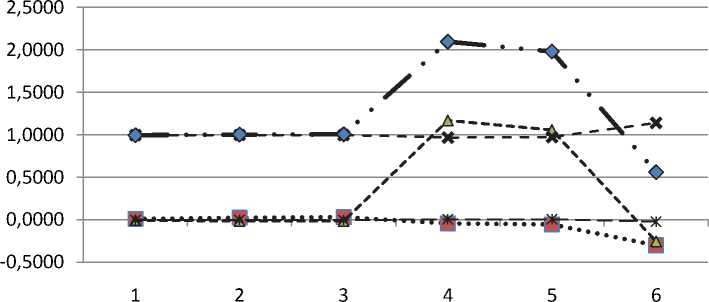
Рис. 2. Динамика показателей степеней производственной функции

Таблица 3

Динамика коэффициентов эластичности

Наименование Номер выборки За период 1 2 3 4 5 6 а 0,0099 0,0228 0,0299 –0,0441 –0,0548 –0,3013 –0,05106 Р –0,0072 –0,0152 –0,0170 1,1682 1,0569 –0,2555 –0,0472 γ 0,9953 0,9969 0,9962 0,9668 0,9722 1,1395 1,0701 δ –0,0036 –0,0029 –0,0034 0,0043 0,0049 –0,0233 –0,0104 Σ 0,9944 1,0016 1,0057 2,0952 1,9792 0,5594 0,9614 a β γ δ Σ вывод, что теснота корреляционной связи только фактора FOT (фонд оплаты труда) с объемом производства ТСЬ демонстрирует постоянство и стабильность, остальные имеют большой разброс, вплоть до отрицательной связи.

Динамика коэффициентов корреляции факторов OA, BnA, Inv показывает, как сильно меняется теснота связи в различных выборках (окнах), что характеризует низкую устойчивость предприятия к внешним воздействиям в период кризиса. Измене- ние воздействий внешней среды, проявляющееся через изменение объемов производства, особенно в условиях кризиса, существенно меняет отдачу (эффективность) факторов производства.

Результаты анализа динамики коэффициентов эластичности (показателей степени факторов) α, β, γ, δ, приведенные в табл. 3, рис. 2, подтверждают

Особый интерес представляет наличие отрицательных значений показателей эластичности выпуска по вещественным факторам производства. На наш взгляд это объясняется необоснованным вовлечением в производство дополнительных ресурсов при неполном использовании имеющихся ресурсов при реальном снижении объемов про-

Таблица 4

Расчетные значения Т? , по окнам

№	Номер окна
	1	2	3	4	5	6
1	76 922
2	88 548	88 476
3	106 594	106 677	106 663
4	110 994	111 022	110 978	115 910
5	97 077	97 119	97 164	100 318	99 971
6	126 006	125 930	125 974	132 135	131 539	125 905
7	135 562	135 570	135 582	142 956	142 344	134 602
8	141 292	141 389	141 428	146 740	146 274	139 902
9	123 660	123 755	123 813	130 489	129 800	118 639
10		180 693	180 767	188 847	188 094	181 010
11			131 892	137 887	137 127	130 153
12				171 828	170 696	161 957
13					162 573	150 774
14						178 469

190 000

170 000

150 000

130 000

110 000

90 000

70 000

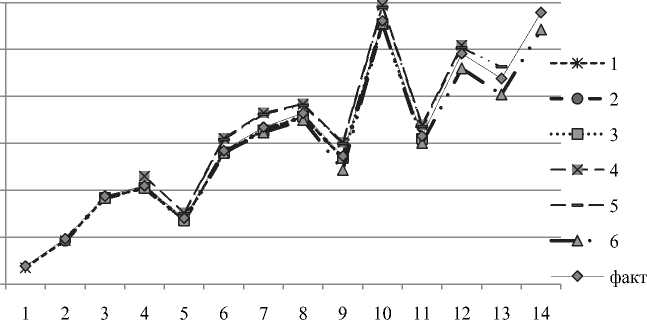
Рис. 3. График исходной (линия – факт) и прогнозных значений за различные выборки (линии 1–6)

вывод о слабой связи факторов с объемом производства. Разброс показателей α, β, γ, δ, при своей низкой значимости за соответствующие выборки, довольно широк. В различные периоды они принимают как положительные, так и отрицательные значения. Интересна положительная динамика значений показателя β в 4 и 5 выборке. Скорее всего, она вызвана отрицательной динамикой значений BnA за соответствующие периоды, при общем росте объемов производства ТС .

Анализ динамики суммы коэффициентов эластичности У, = а + Р + у + 5, т. е. масштаба производства, позволяет сделать вывод, что на масштаб производства кризисные явления влияния не оказывают.

изводства (см. наблюдения № 5, 9, 11, 13 табл. 1). В равной степени это относится и к инновационноинвестиционной деятельности.

На динамику коэффициентов эластичности повлияло следующее:

• –    высокий уровень эластичности фонда оплаты труда определяется действующей негибкой системой мотивации труда, а также высокой долей заработной платы основных рабочих;

• –    низкий уровень эластичности внеоборотных активов понятен и объясняется их экономической природой;

• –    низкий уровень эластичности оборотных активов, скорее всего, обусловлен недостаточно эф-

• фективной системой управления оборотным капиталом;

  – низкий уровень показателя эластичности инвестиций и его отрицательная корреляция вызваны временным лагом между моментом проведения капиталовложений и их отдачей, а также низкой загрузкой оборудования. Анализ влияния величины инвестиций на эффективность производства, по мнению авторов, надо проводить на значительно больших временных интервалах.

Таблица 5

Динамика средней относительной ошибки аппроксимации

Наименование	Выборки
	1	2	3	4	5	6
Eo	0,0087	0,0085	0,0083	0,0348	0,0301	0,0267

Необходимо отметить, что вероятностные модели дают лишь оценки коэфициентов регрессии. Анализ верифицируемости полученных оценок относительно фактических данных достигается проверкой статистической значимости коэффициентов регрессии и близости расположения фактических данных к рассчитанной линии регрессии [3, с. 271].

Для оценки точности модели использована средняя относительная ошибка аппроксимации, т. е. статистическая значимость коэффициентов определялась степенью вариации вокруг оценочного значения. Полученные результаты, приведены в табл. 5 и на рис. 3:

Ео = ^2 l^^l •lOO %, (4)

п 1 с [ где n - количество наблюдений; ТС, - расчетное значение переменной i - го периода; ТС, - фактическое значение, для выборок 1–6.

Средняя ошибка аппроксимации укладывается в диапазон от 0,85 до 3,48 %, что позволяет сделать вывод о высокой достоверности построенной модели.

Результаты расчетов критерия Фишера (F-статистики) приведены в табл. 6. Расчетные значе- ния больше табличного на всех периодах, что отражает достоверность результатов.

Таблица 6

Динамика F-критерия

Наименование	Выборки
	1	2	3	4	5	6
F	360,27	506,77	386,06	21,13	24,37	5,76

На основании анализа динамики показателей производственной функции можно сделать сле- дующие выводы.

• 1.    Необходимо осторожно подходить к вопросам подбора факторов. Рациональной базой для включения и исключения факторов в модель может служить теория, лежащая в основе модели.

• 2.    Предлагаемый метод на основе производственной функции, позволяет не только оценивать влияние факторов производства на конечный продукт, но и проанализировать динамику эффективности (пропорциональности) этих факторов (затрат соответствующих ресурсов).

• 3.    Предложенный метод диагностики и прогнозирования динамики факторов производства позволяет значительно повысить точность и достоверность прогноза.

• 4.    Для обеспечения достоверности результатов моделирования необходимо исследовать влияние числа степеней свободы выборок на значимость коэффициентов регрессии.