Динамический синтез пружинно-зубчатой муфты

Трансмиссия находится в рабочем состоянии – установившийся режим. Расчетная модель с учетом упругости валов, но без учета диссипативных сил, представляется трехмассовой. Система дифференциальных уравнений имеет вид:

Jхфх + С12(Ф1 - ф2) = M p

J2ф2 - c12 (ф1 - ф2 ) + c23( ф2 - ф3) = 0,

B 2 =-

^c 23 ^{ф( c} 23 ^J 2 ^в 1 ) в 2 J2<в 2 " вх^

В ² = -^c 23- r ^р1,2    2 J ₂

^c 12^{( J} 1 ^{+ J} 2 ) ^c 23 ^J 1

^c 12^{( J} 1 ^{+ J} 2 )

^c 23 ^J 1

„ T

) 2   ^{4 c} 12 ^J 2 ]

^c 23 ^J 1

где ф i , ф ₂, ф₃ - обобщенные координаты, углы поворота масс с моментами инерции J 1 , J ₂, J ₃. На рисунке J 1 - приведенный момент инерции вращающихся масс привода трансмиссии; J ₂ -приведенный момент инерции муфты: J ₂ = J ₂ ‘ + J₂ - _ ^J ₂ - , J₂ ‘ - моменты инерции полумуфт; J 3 - приведенный момент инерции исполнительного органа; c ₁₂, c ₂₃ - пиведенные жесткости валопроводов, Осуществив переход к обобщенным координатам M ₂₃= c ₂₃( ф ₂- ф ₃) -упругим моментам на валах система (1) преобразуется к виду:

Mi, + В M12 + С12 M 23 = ^, J 2

2        С 23          С 23 M 3

M + β M - M =-

23      23    2312

J2            J3

_Гд_е R ² _{= с} ^J 1 ^{+ J 2} В ² = с J ^{2 +} J ^{3 |де в} 12 ^С 12 _т , , ^В 23 ^С 23 г _Л .

^J 1 ' ^J 2                    ^J 2 "  ^J 3

Первая фаза (рис. 1б). Возникает стопорная нагрузка. Масса с моментом инерции J ₃ останавливается. Расчетная модель для напряженного состояния представляется следующей системой дифференциальных уравнений:

mx 2 + s^M 2 - -12 m2 , = -12 mx 12      12    12             231

J 2

, m9 ,+e?3 m, 3 —23 m,2 = 0 23      23   2312

J 2

, где в12 = -12(J1 + J2)/J1J2 B^ = c23/J2, M 23 = c23Ф2.

Решение данной системы имеет вид:

M12 = A1 sin в11 + B1 sin в21 + M 1,

M23 = A2 sin Д1 + B2 sin в21 + M 1, где A = A2(1 J231 / c23),

B 1 = B 2 (1 - J 2 в./ c 23 ),

A 2 =-

^c 23 ^{ф ( c} 23   ^J 2 ^в 2 )

в 1 J ₂( в 2² — в ')

В этот момент возрастает давление на грани зубьев [3]. Для оценки состояния системы необходимо учитывать возникающее осевое усилие Q (рис. 2).

Q = P n (sin( a - р' ) - в 1 R cos( a - р )/ r )

P n = M ₂₃ /( Rcos ( ^а - Р ) )

где P n - сила нормального давления на грани зубьев, а - угол наклона рабочей грани кулачка, р - угол трения на кулачке (tg( p ) = в - коэффициент трения), в 1 - коэффициент трения муфты на шлицах, R - средний радиус муфты, измеренный по кулачкам, r - радиус вала или радиус впадин шлицевого вала подвижной полумуфты. На рисунке обозначено T = M ₂₃/ R tg( а р ) - осевая сила, Т - сила трения втулки подвижной полумуфты на шлицах втулки T = в 1 M ₂₃/ r . Как только это усилие станет положительным, то происходит осевое движение ведомой полумуфты.

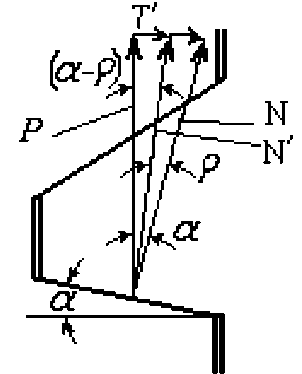
Рис. 2. Расчетная схема

Вторая фаза (рис. 1в). Относительное перемещение полумуфт. Расчетная модель для напряженного состояния представляется следующей системой дифференциальных уравнений [3]

M,„. + В2.М„. -c.M. - / J . = 12       12     12       12     2 2      2 пр

с 123 (М1J2' + Mр J 1)/( J1J2')

M... + в. I- M. v - cM.J J. +

2 2       2 2     2 2       2 2     12     2 пр с^- Mt /IJ" =- M,Av( J, + J J/( J J J

2 2 ^a 2          ^p 2 2    2     2 ^22

, лл         ²

^M 2" 3 ⁺ Р т3 ^M 2" 3 ^c 2'3 ^M 2'2" ^{1 J} 2"    c 2"3 ^M p ^{1 J} 2"

, m2" x2" + cnp (x° - x2" ) = Pn (sin(^ - P) -p1 R cos(a - p) signx I r

M _p = RP n (cos( a - p ) + p sin( a - p ) signX ) X sign ф ^- Ф у)

где в12' = c12'(J1 + J2' np )I( J1J2' np ) , в2" n = cnp 1 m 2'' , вТТ = c2'2" ( J2' np + J2'') I( J2' npJ2'') , в2"з = c 2-' з 1 J2" C12' = C12 c 2''3 = c 23

,                              ,                                ,

M ₁₂ ' = c ₁₂ ' ( Ф 1 — Ф ₂ ' ) M ₂'₂ " = c ₂'₂ " ( ф ₂■ — Ф ₂ " )

,

,

M2‘3 c2‘3^2’, m2 = m —масса подвижной по-

лумуфты; xr x - угловое и осевое перемещения подвижной полумуфты, x ° = x ₀ - начальное натяжение пружины; ^c 2-3 - крутильная жесткость вала от ведомой полумуфты до преграды, ^J 2 ' пр приведенный момент инерции ведущей полумуфты ^J 2 ' np = ^J 2 ' ⁺ m 2 " ^{R 2 tg a} . Полумуфты связаны упругой связью, жесткость которой равна приведенной жесткости пружины с ₂ ' ₂ '' . с 22• = ^C np ^R /[ tg^{( а -} P ) ^- R P 1 ¹ r ] . Для правильного сцепления кулачков подвижная муфта должна передвигаться по валу без качения, что достигается при помощи шлицевого соединения или посадкой полумуфты на двух диаметрально противоположных направляющих шпонках. Статический момент срабатывания муфты:

^M cm = ^P np ^{R I[} tg ^{( a} - P ) - P 1 ^{R 1} r ^]

Наибольший крутящий момент (М) складывается из статического М _ст и динамического М д моментов: М = М _ст + М д . Для определения динамического момента рассмотрим движение подвижной полумуфты. Динамический крутящий момент М д при проскальзывании кулачковой муфты определяется:

Md = c2,3 • ф2- sin(p1t) I p1

где p 1 - круговая частота собственных угловых колебаний подвижной полумуфты p1 = cc2,'31J2" , to = ф2- - угловая скорость подвижной полумуфты.

Третья фаза (рис. 1г). Полумуфты выйдут из зацепления. Установившийся процесс проскальзывания можно представить состоящим из следующих этапов: а) полумуфты разобщены (скольжение по торцам и вход кулачков ведущей полумуфты во впадины другой); б) удар и скольжение кулачков ведущей полумуфты по кулачкам ведомой. Подвижная полумуфта совершает угловые и осевые колебания в направлении упругих связей в двух взаимно перпендикулярных плоскостях. Возникают две системы: двухмассовая и одномассовая. Перемещение подвижной полумуфты, обладающей двумя степенями свободы можно привести к двум перемещениям с одной степенью свободы. Расчетные модели для напряженного состояния представляются следующими системами дифференциальных уравнений [2-3]. Для двухмассовой системы:

M12' + в122' M i2' = ci2' M1 / J1 , где в122' = c12'(J1 + J2')/(J1J2) . Данное уравнение описывает вынужденные колебания масс 1 и 2 под действием постоянного приведенного момента двигателя М1. Для одномассовой системы:

•&           2

^M 2 '' 3 ^{+ в} 2 '' 3 ^M 2 '' 3 = ⁰

^Х 2 '' ^{+ в} 2 '" n x 2 "

= 0

где ^в 2 3 = ^c2- 3 ^{1 J} 2 '' , ^в 2 " n = c np ¹ m 2 '' .

Это означает, что ведомая полумуфта совершает крутильные колебания вокруг оси и линейные колебания под действием пружины. Эта полумуфта перемещается в осевом направлении не более, чем на высоту зуба h ₃ = h , т.е. муфта проходит расстояние AB =2 h sin а (рис. 3).

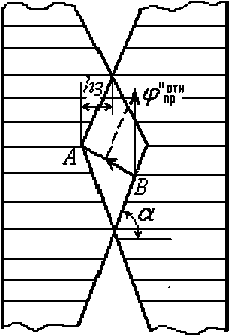
Рис. 3. Схема определения времени движения полумуфт до их зацепления

Относительная приведенная скорость полумуфт

v2’2, = R (m2' - шт) + X2.tg (a)

1t3                                                        ■ где ®2' = ~ JM12'dt + ®2'(0) ,

J 2 ' 0

1 t ³

m ₂ - = ——J M ₂ ' ₃ dt + ^ю ₂"(₀) - угловые скорости

J 2 ' 0

полумуфт в начале третьей фазы. Замыкание полумуфт происходит при условии

2 h ₃ sin а = R cos а

t 3

J to^ " ^dt

В момент замыкания возникает удар. Прини- мая соударение пластическим и мгновенным имеем:    J2‘m2'(3) + J2"®2P(3) = m2 J2 .

скорость муфты после

® 2    ® 2 " (3)^J 2 ' / ^J 2 ⁺ ® 2 P (3) ^J 2' ^{I J} 2 ’

Угловая удара где

m ₂ ^p ₍₃) = to _{Y (3}) + X_{Y (3}) tg a I R - приведенная скорость ведомой полумуфты в конце третьей фазы; to ₂" (3) , X 2"(3) - угловая скорость ведущей и линейная скорость ведомой полумуфт в конце третьей фазы, т.е. до удара. Отсюда после удара: М 12 ' ( у ) = С 12 ' ( ^ - » ₂ ) , ^М 2"3( y ) = c 2 '' 3 ^ 2 • Во время соударения возникают нормальные p n и тангенциальные p t импульсы, которые вызывают соответствующее изменение скоростей [3]:

m [ X ( + 0) - X ( - 0)] = - p_n sin a ± p_t cos a J ₂ ' [^ ^ 2 ' ( + 0) - ф_г ' ( - 0)] = p _n R cos a ± p _t R sin a J 2 ' [Фх ( + 0) - Ф₂ ' ( - 0)] = - p_nR cos a + p_tR sin a

Время t, необходимое для смещения подвижной полумуфты под действием пружины на расстояние h , равное высоте кулачка

.    1     „ h .

t1 =—arc cos(1--), p 2           x 0 + h где р22=спрIm - круговая частота собственных осевых колебаний подвижной полумуфты, t1 -время, через которое наступает соприкосновение полумуфт. Время t2, за которое ведущая полумуфта повернется на угол, соответствующий окружному смещению кромок у вершины и основания кулачков из-за наклона рабочей поверхности: t2=h tgaI(to0R)

•x ^{( - 0)} > J^ Rtg ( a + p ) ^ 2,2 ' ( - 0)1

J 2

Послеударные скорости:

( 9 ₂,₂ '' ( + 0) = ^ & ₂,₂ '' ( - 0) I B 1 + Xc ( - 0) I B ₂

X ( + 0) = ф₂,₂, ( - 0) I B ₃ + J& C - 0) I B ₄

где B1 = 1 +

_   _        J_Ptg a^ tg ( a + p ),

B2 = Rctga[1 +    ---——],

J 2

B3 = tg^[1 +

R     J ₂ ,tg a ■ tg ( a + p )

^J 2 . tg ^a^ tg ^{( a} m p )

^B 4 =^{1 +}----------------

J ₂

Полученные послеударные значения угловых скоростей, моментов являются начальными для дальнейшего моделирования. Расчет муфты сводится к определению: допускаемого напряжения на срез в шлицах, размеров пружины. Решающую роль в работе муфты играет скорость ее выключения и надежность. Эти показатели зависят от вида кулачков (прямоугольные, трапецеидальные), их количества и расположения. Исследование действительных значений упругих моментов в валах машины при заклинивании исполнительного органа позволяет принять решение о работоспособности муфты. На этапе проектирования необходимо оценить данные моменты, исследовать влияние конструктивных параметров муфты и трансмиссии, а также влияние скорости вращения привода на коэффициент динамичности [2-4].