Динамическое моделирование наноразмерных систем

татус математического моделирования как «третьего метода познания» в настоящее время общепринят. В большинстве областей науки и техники средства математического моделирования занимают равноправное положение вместе с теорией и экспериментом.

Натурные исследования наноразмерных системами подчас являются дорогостоящими и осложняются специфическими для данного масштабного уровня требованиями к измерительному оборудованию. В частности, многие методы вносят в процесс измерения недопустимые искажения: зонд атомно-силового микроскопа может необратимо изменить поверхность объекта, а интенсивное излучение осветителя оптического микроскопа может вызвать нежелательные фазовые переходы.

Использование инструментария математического моделирования – предпосылка получения качественно новых результатов в прорывных областях, связанных с разработкой наномодифицированных и наноструктурированных строительных композитов. Актуальность разработки методов моделирования наноразмерных систем обусловлена устойчивым повышенным интересом к свойствам и областям практического использования указанных систем.

Выбор методов, алгоритмов и инструментальных средств моделирования в первую очередь определяется масштабным уровнем, представляющим для исследователя наибольший интерес. На нижнем масштабном уровне (менее 10 нм) для исследования удается привлечь модели, полученные из первых принципов, однако при переходе к следующему масштабному уровню – 10...100 нм – эти модели постепенно теряют вычислительную пригодность [1]. Начиная с этого масштабного уровня, становится целесообразным применение метода частиц.

Термин «метод частиц» является собирательным для большой группы методов, оперирующих с системами дифференциальных уравнений основного закона динамики. Многочисленные модификации метода частиц, ориентированные на моделирование наноразмерных систем, называют методами молекулярной динамики. Эти методы привлекают в тех случаях, когда интерес представляет не только установившееся состояние, но и эволюция нанообразований, а также фазовые переходы в наноразмерных областях.

Особенностью связующего, наполняемого тонкодисперсным материалом, к поверхности частиц которого привит (или иным образом перераспределен из вяжущего в массиве) наномодификатор, является наличие сравнительно больших тангенциальных сил, возникающих при взаимных перемещениях структурных элементов верхнего масштабного уровня (микроструктуры строительного композита). Необходимость учета указанных сил затрудняет использование известных программных пакетов молекулярной динамики.

В ряде работ (например, [2, 3]) исследуемая дисперсная система представлена моделью

mzT,.-^.(r,.-vz.)=-Vt/-, i = X,N

где mi – масса i-й частицы; ri = (xi; yi; zi) – ее координаты; ki – коэффициент, определяемый диссипативными свойствами дисперсионной з Д среды; vi – скорость дисперсионной среды в точке ri; V У

/=i

e, — – опе-

1 OX:

ратор Гамильтона; U _i – потенциал в точке r _i (зависящий от характеристик дисперсионной среды, а также от характеристик и взаимного расположения всех остальных частиц системы).

При решении некоторых задач система обыкновенных дифференциальных уравнений (1) может быть записана в форме, допускающей аналитическое решение. Так, в работе [4] при исследовании характерных параметров процесса кластерообразования выполнено аналитическое исследование модели (1) для ряда предельных ситуаций (значительное межчастичное расстояние, однородное взаимное расположение, пренебрежимо малая вязкость дисперсионной среды).

В общем случае система (1) аналитического решения не допускает. Ее левая часть, являющаяся разностью сил инерции и вязкого трения, неизменна по форме. Потенциал парного взаимодействия обычно определяют выражением с заданным числом минимумов, соответствующих положениям равновесия.

В частности, он может быть принят в виде

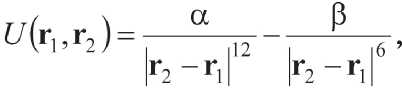
α >0, β >0,

где r₁ , r₂ – координаты частиц.

Выражение (2) содержит два независимых параметра, численные значения которых зависят от:

– расстояния r _m = | r₂ – r₁ |, соответствующего положению равновесия, для которого ∇ U | _r=r = 0 ;

– глубины потенциальной ямы U _m = –U ( r _m ).

Как глубина потенциальной ямы, так и расстояние, соответствующее минимуму потенциальной энергии, определяются на основе анализа физико-химических процессов в дисперсной системе.

В [4] для определения расстояния r _m был использован энергетический подход. Получено выражение

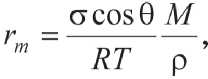
где θ – краевой угол смачивания; M – молекулярная масса вяжущего; σ – поверхностное натяжение вяжущего; ρ – плотность вяжущего; R – универсальная газовая постоянная, T – температура, K.

Потенциал в правой части (1) можно записать в виде

^=^.»+y,,g+f^,                           (4)

j*i где Ui,b – потенциал взаимодействия с границами; Ui,g – гравитационный потенциал; Uij,p – потенциал парного взаимодействия; N – число частиц.

Учет влияния наномодифицированного наполнителя может быть произведен параметрами выражения потенциала парного взаимодействия. Последний в наиболее общей ситуации выбирается в виде Леннарда–Джонса

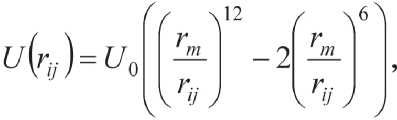
где r _ij – расстояние между поверхностями частиц; U ₀ – характерная энергия взаимодействия; r _m – расстояние, соответствующее положению равновесия.

Для описания эволюции дисперсных систем, между частицами которых действуют силы отталкивания, можно использовать (5) при сохранении только первого слагаемого.

Выбор потенциала взаимодействия с границами области должен обеспечивать финитный характер движения частиц.

Полагая скорость частицы v _i = г _i в качестве новой переменной, систему (1) можно записать как 6N обыкновенных дифференциальных уравнений первого порядка

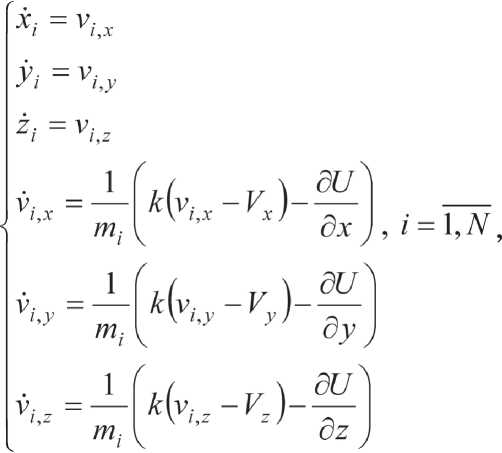
где N – число частиц.

С целью исключения операции разностного дифференцирования по пространству вместо потенциала U следует использовать модуль силы парного взаимодействия (действующей вдоль прямой, соединяющей центры i -й и j -й частиц), модуль силы взаимодействия с границей области (действующей вдоль проходящей через i -ю частицу нормали к границе области), силу тяжести и силу вязкого трения

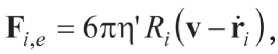
действующую со стороны дисперсионной среды. Система (6) примет вид:

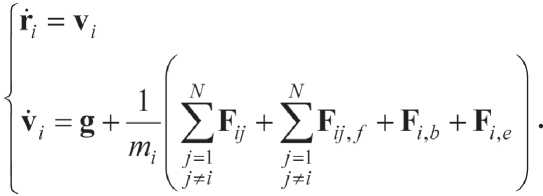
Ее можно представить в форме

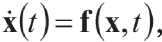
где x = ( r₁ , r₂ ,..., r _N , v₁ , v₂ ,..., v _N ) – радиус-вектор системы частиц в 6N -мерном фазовом пространстве.

Учет сил вязкого трения, действующих на частицу верхнего структурного уровня со стороны ближайших таковых, окруженных слоями наномодифицированного связующего, может быть выполнен следующим образом. Пусть частицы (полидисперсные сферы) окружены слоями толщины d _g .

Примем, что искомая сила F _ij,f , j = 1,2V, подчиняется закону вязкого трения Ньютона и отлична от нуля в случае ненулевой площади S _ij , по которой перекрываются окружающие частицу слои. Для площади S _ij имеем

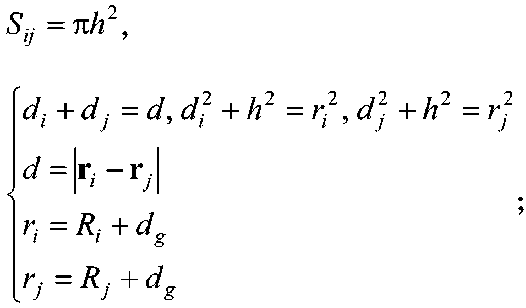
7.2 _      ,2 _ 21/2   2,2^•

/7 - Г- (2; — Г:        . Г Г; A" d ;(12)

Sg = ^ (R, + d J - ^y ((r, + d J - (r , + d J + (r, - r J ) ,(13)

Е.В. КОРОЛЕВ и др. Динамическое моделирование наноразмерных систем где r2 = r•r = r2 – скалярный квадрат.

Сила Fij,f действует в плоскости сечения Sij и пропорциональна про- екции vi,t скорости частицы vi на плоскость сечения:

17    _        4 х f —                  .

'' K R,

Искомая тангенциальная сила – проекция v _i,t – равна

V = v — v.

1,1 I i,n , где

^i^^.'Yij^Y^ ,

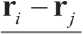
– орт вектора r _i – r _j , соединяющего центры j -й и i -й частиц.

Предложенные алгоритмы моделирования реализованы в переносимом (платформы POSIX – FreeBSD, Solaris, Linux – и Microsoft NT – Windows NT 4.0...Windows 7) модульном автономном программном обеспечении. Переносимость достигается на уровне исходного кода, посредством изоляции платформенно-зависимых функций в каркасную библиотеку с минимальной необходимой функциональностью [5].

На платформе Microsoft NT вычислительное ядро может быть дополнено графическим интерфейсом пользователя. Блок интерфейса взаимодействует с ядром посредством текстовых заданий, записанных на проблемно-ориентированном алгоритмическом языке описания систем частиц.

Исполнение вычислительного ядра начинается с синтаксического разбора командной строки, в которой пользователем (возможно, посредством интерфейсного блока) передается имя управляющего задания. Расчетное задание содержит текстовое описание моделируемой системы, в котором определены общие параметры системы (число частиц – полидисперсных сфер, распределение частиц по размерам и плотности), начальные условия (пространственное распределение частиц), расположение и вид границ, вид функций парного взаимодействия и взаимодействия с границами, численные значения параметров, входящих в выражения для функций взаимодействия.

Перед первым вызовом процедуры вычисления правой части (9) треугольные матрицы (размера NxN) расстояний и сил разбиваются на линейные блоки. Число блоков совпадает с числом вычислительных ядер (произведение числа центральных процессоров на число ядер в центральном процессоре использованной платформы). Инициализацию параллельного планировщика завершает создание потоков исполнения и вспомогательных объектов блокировки и ожидания. В момент создания нитям исполнения передаются аргументы, однозначно идентифицирующие элементы блока, подлежащие обработке в соответствующей нити.

При каждом вызове процедуры вычисления правой части системы (9) происходит освобождение объектов блокировки; в нитях выполняется расчет сил парного взаимодействия (в т.ч. – учет тангенциальных сил для частиц, находящихся по отношению друг к другу на расстоянии меньше некоторого предельного), по завершению которого из нитей объекты блокировки устанавливаются в закрытое состояние. Нити ожидают их освобождения при следующем вызове процедуры вычисления правой части, в основной нити выполняется нахождение сил взаимодействия с границами и дисперсионной средой.

В процессе моделирования регистрируются статистические оценки энергетических и топологических показателей дисперсной системы. Результаты численного эксперимента представляются вычислительным ядром в csv-формате и на интерпретируемом языке пакета 3DS MAX, который на платформе Microsoft NT может быть использован для визуализации пространственных конфигураций исследуемой системы.

Уважаемые коллеги!

При использовании материала данной статьи просим делать библиографическую ссылку на неё:

Королев Е.В., Смирнов В.А., Иноземцев А.С. Динамическое моделирование нанораз-мерных систем // Нанотехнологии в строительстве: научный Интернет-журнал. М.: ЦНТ «НаноСтроительство». 2012, Том 4, № 3. C. 26–34. URL: (дата обращения: ______________).

Dear colleagues!

The reference to this paper has the following citation format:

Korolev E.V., Smirnov V.A., Inozemtcev A.S. Dynamic simulation of nanoscale systems. Nanotechnologies in Construction: A Scientific Internet-Journal, Moscow, CNT «NanoStroitelst-vo». 2012, Vol. 4, no. 3, pp. 26–34. Available at: (Accessed _____________). (In Russian).