Динамика антропоморфных демонстрационных роботов
Автор: Урмакшинова Елена Рониславовна, Мархадаев Баир Ендонович
Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths
Рубрика: Математическое моделирование и обработка данных
Статья в выпуске: 4, 2016 года.
Бесплатный доступ
В статье рассмотрены подходы к решению задач динамики демонстрационных роботов, преимущественно антропоморфных. Особенностью демонстрационных роботов является ориентация на зрительское восприятие при наличии в их составе не слишком сложных механизмов и исполнении чаще всего циклических движений. На примере двухзвенного механизма, представляющего руку робота, приведен расчет частот колебания звеньев. Также представлены общие формулы для расчета колебаний при наличии упругих элементов.
Демонстрационный робот, колебательные свойства, антропоморфный, динамика
Короткий адрес: https://sciup.org/14835201
IDR: 14835201 | УДК: 621.865 | DOI: 10.18101/2304-5728-2016-4-69-75
Текст научной статьи Динамика антропоморфных демонстрационных роботов
Понятие «демонстрационные роботы» было введено сравнительно недавно. К демонстрационным роботам относятся механические устройства, подвижные или с подвижными составными частями, с автоматическим управлением, которые не выполняют никаких производственных функций, а демонстрируют или сами себя, или другие объекты. Демонстрационные роботы широко используются в рекламе и также с успехом используются как тренажеры. Новая область применения демонстрационных роботов, больших движущихся фигур, относится к механическому оснащению сцены.
Основными отличительными чертами демонстрационных роботов являются: наличие не слишком сложных механизмов, движение составных частей механизмов, ориентация на зрительное восприятие [1].
Во всех случаях при разработке внешних форм любого демонстрационного робота значительное место обычно принадлежит дизайнерам. С другой стороны, современный демонстрационный робот представляет собой автоматически управляемую систему, часто с совершенным компьютерным устройством управления. Однако есть все основания считать, что все же чаще всего основная проблематика создания демонстрационных роботов заключается в механике, начиная с выбора рациональных кинематических схем, и кончая созданием систем автоматического управления [2].
Так как демонстрационные роботы в подавляющем большинстве представляют собой имитацию человека или животного с активным движением конечностей, позвоночника, необходимо уметь рассчитывать колебательные свойства их звеньев.
Если задавать законы движения звеньев во времени, то формулируется прямая задача динамики. Решение этой задачи дает требуемые законы изменения обобщенных сил (моментов, создаваемых приводами). Динамические погрешности отработки программ, хотя и являются второстепенным фактором, поскольку зрительно не воспринимаются, все же в определенных режимах могут представлять интерес. Для определения динамических погрешностей необходимо решить обратную задачу динамики для механизма с учетом характеристик приводов, интегрируя систему дифференциальных уравнений движения системы.
Исследование динамики антропоморфных демонстрационных роботов
Уравнения Лагранжа механической системы относительно обобщенных координат в общем виде:
d (д T ) д T S П
--I--=— + Qi dt ^ д q, J д q, д q, где T - кинетическая энергия, выраженная через обобщенные координаты, обобщенные скорости qi, время t, П - потенциальная энергия, a Qi -обобщённые непотенциальные силы.
Обобщенные силы удобно представить в виде сумм
Q = Qi(1)( q„ q,) + 0(2 (Uj, q„ q,), где uj - параметр воздействия, задаваемого приводом. Первое слагаемое определяется только свойствами самого механизма, второе - воздействием привода, далее звенья механической системы считаются жесткими телами, однако дополнительно можно ввести в рассмотрение «упругие» степени свободы и при составлении уравнений Лагранжа считать их равноправными.
В качестве иллюстрации методики расчетного определения колебательных свойств конечности демонстрационного робота рассмотрим для примера двухзвенный шарнирный механизм. Система уравнений Лагран- жа записывается в виде одного матрично-векторного уравнения: d faT) дT ,, дП
I= M .
dt (д ф ) д ф д q
Здесь M —
M 1
M 2
- вектор-столбец управляющих моментов, ф - вектор
столбец межзвенных углов, дП дф
д П дф 1 д П
дФ2 .
.
A —
ml 2 ml 2
+ mJ, + —2L 3213
+ m 2 1 1 1 2 cos ф 2
ml 2
2 2 2 + m 2 1 1 1 2 cos ф 2
ml 2
2— 1^- + m 2 1 1 1 2 cos ф 2
m 2 l 2
,
где m 1 – масса первого звена, m 2 – масса второго звена, l 1 – длина первого звена, l 2 – длина второго звена.
П — 0,5 m1 g1 1 sin ф 1 + m 2 g ( 1 1 sin ф 1 + 0,5 1 2 sin( ф 1 + ф 2 ). (5)
После подстановки получаем систему уравнений
. В1\ ф 1 +В 12 ф 2 + В 13 ф 1 ф 2 + В 14 ф 2 B 10
B 21Ф1 + B 22ф2 + B 23ф1Ф — B 20
где
B 11 — A n , B 12 = B 21 = 2 A 12 , B 13 — m 2 1 1 1 2 sin ф 2 ,
B 14 — B 23 —- 0.5 m 2 1 1 1 2 sin ф 2 ,
B 10 — M 1 - 0.5 m 1 g1 1 cos ф- - m 2 g1 1 cos ф- - 0.5 m 2 g1 2 cos( ф 1 + ф 2 ),
B 22 — 13 m 2 1 2 ,
B 20 — M 2 - 0.5 m 2 g1 2 cos( ф 1 + Ф 2 ). (7)
Так как закон движения звеньев известен, то, подставив выражения для ф i ( t ) и ф 2( t ): в систему уравнений (6), получим требуемые обобщенные моменты M 1 и М 2 .
Исследуем далее частоты колебаний звеньев [3]. Для этого представим углы в следующем виде:
< ф 1 — ф 10 ( t ) + V 1( t ), _ ф 2 — Ф 20 ( t ) + V 2 ( t ),
где ф 10( t ) и ф 20( t ) - номинальные значения углов ф 1 и ф 2 , а v 1 ( t ) и V 2 ( t ) — их упругие составляющие.
Тогда уравнение для потенциальной энергии примет вид:
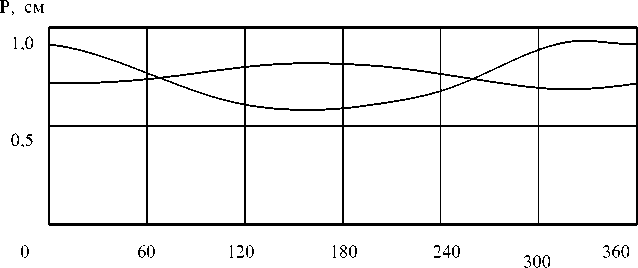
П = П1 + 2 Учитывая, что в этом случае Vi | = ф и из уравнений (6) получим линеаризованное матричное дифференциальное уравнение: Вф+Су=В0, (10) где B= B11 B21 B12, C= c1 B22 J , L 0 Здесь в коэффициентах Bij вместо значений ф1, ф2 взяты их средние (номинальные) значения ф10, ф20. Известно, что общее решение соответствующего однородного уравнения имеет вид: V = Pcos tot = P1 P cos tot, а общее решение исходного матричного уравнения будет иметь вид: V = P cos tot + R = P1 P2 cos tot + B10 c1 B20 c2 где R – частное решение уравнения (10). Из условия существования нетривиального решения получаем частотное уравнение в общем виде —Buto2+ Ci — B^to2 - B 21 to — B 22 to + C 2 После раскрытия получаем биквадратное уравнение вида: ato4 + bto2 + c = 0, где в данном случае a = B11B22 — B122, b = c1 B22 + c2Bn, с = с с2. Отсюда 2 c1B22+ c2B11 ± J(c1B22— c2B11)2+ 4 c1c2B22 to, 2=------------------- ------------------ 1,2 2( B11B 22 — B2) Рис. 1 Именно эти собственные частоты являются определяющими при выборе параметров системы. Амплитуды колебаний находим из начальных условий v = 0, P = R. Очевидно, что частота колебаний о зависит от конфигурации рассматриваемого двухзвенника. На рис. 1 приведен график изменения частоты о от межзвенного угла ф2, при этом m 1 = 2 кг, m2 = 1,5 кг, 11 = 0,5 м, 12 = ,4 м, c1 = 200 кг-м/рад, с2 = 150 кг-м/рад. На рисунке 2 приведены амплитуды колебаний для этого же механизма, если закон движения задается в виде: Ф1( t) = ®01 Ф2( t) = 30 t. Рис. 2 То есть первое звено вращается равномерно, а второе звено по отношению к нему вращается в три раза быстрее, в этом случае траектория конца второго звена описывает эпициклоиду. Подставив соотношения (16) в (10) получим Pi P2 о 2 P =---( Вп + 3 В„ ), cl Р =— 5 1 2 ^23 . c 2 Уравнения приводов записываются по-разному в зависимости от того, какие приводы используются. Для неуправляемого реверсивного линейного привода обычно в первом приближении записывается уравнение вида d2u, du, Tj^d" + Л7 = P. -<t) - Fj<Qi )■ dt dt где Vj Tj^f + = -u-< t) — S-< t)] — F-< Qi), <18) dt dt где sj В случае необходимости в модели может быть учтена упругость элементов конструкций, причем для рассматриваемых задач достаточно учитывать только сосредоточенные упругости в кинематических парах. Для задач динамики демонстрационных роботов влияние характеристик приводов при контурном управлении практически сводится к сглаживанию возможных скачков программных функций и к запаздыванию, причем запаздывание для различных обобщенных координат может быть существенно различным. Поскольку в самой программе движения обычно предусматривается запаздывание одних звеньев относительно других, то очевидно, что учет динамики в таком плане, не меняя общего характера движения, лишь изменяет параметры. Заключение Сформулированы, формализованы и решены для типовых структурных схем антропоморфных демонстрационных роботов задачи динамики. Динамика механизмов в обобщенных координатах представляется в форме уравнений Лагранжа второго рода, динамика приводов, неуправляемых или управляемых, задается линейными уравнениями первого порядка. Для некоторых простых механизмов учитываются сосредоточенные упругости в кинематических парах. Определены критерии и факторы, которые нужно учитывать при выборе приводов, режимов их работы и при программировании их движе-74 ний. Сформулированы критерии для динамических режимов упругих колебаний механизма антропоморфного демонстрационного робота при учете упругости элементов, определены подходы для исследования колебаний, возникающих во время движения и после остановки.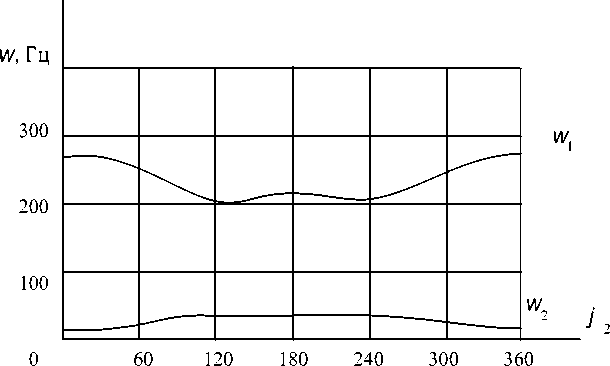
Список литературы Динамика антропоморфных демонстрационных роботов
- Челпанов И. Б., Урмакшинова Е.Р., Никифоров С.О., Бальжанов Д. Ц. Принципы реализации приводных устройств демонстрационных роботов//Матер. II междун. конф. «Проблемы механики современных машин». -Улан-Удэ: Изд-во ВСГТУ, 2003. -Ч. 3. -С. 45 -50.
- Мархадаев Б.E., Никифоров С.О., Челпанов И. Б. Змееподобные демонстрационные роботы для представлений и шествий//Матер. VI междун. конф. «Проблемы механики современных машин». -Улан-Удэ. Изд-во ВСГУТУ, 2015. -Т. 3. -С. 39 -44.
- Мархадаев Б.E., Никифоров С.О. Модульное структурное проектирование безреверсных манипуляторов//Вестник машиностроения. -2013,-№ 07.-С. 41-47.


