Динамика газожидкостной среды в угольном пласте

Проблемы охраны окружающей среды выдвигают в качестве важнейшей задачу исследования миграции загрязненной солесодержащей воды (флюида) в угольных пластах. Так как угольные пласты являются, как правило, неоднородными и имеют трещиноватую структуру, то требуются новые численные модели, позволяющие учитывать неоднородность и анизотропию пористого скелета, а также пространственный характер движения двухфазной среды в пласте.

Теория двухфазной фильтрации базируется на обобщенном законе Дарси, справедливом для медленной стационарной фильтрации несмеши-вающихся сред. Согласно обобщенному закону Дарси, неподвижная пористая среда и одна из подвижных фаз рассматриваются как некая фиктивная пористая среда, в которой происходит фильтрация другой фазы. Такая схематизация предполагает, что при медленном стационарном течении формируется равновесное распределение фаз, которое в процессе двухфазной фильтрации сохраняется статистически постоянным. В процессе двухфазной фильтрации формируется фиктивная пористость, состоящая из активных, соединяющихся между собой пор, образующих ка- налы, по которым происходит движение фаз, и из застойных зон, где фазы неподвижны, или находятся в состоянии медленного циркуляционного движения. Смачивающая и несмачивающая фазы движутся каждая по своей системе каналов. Движение каждой из фаз происходит под действием своего фазового давления, а проницаемость фиктивной пористой среды определяется своей фазовой проницаемостью.

Эти результаты позволяют распространить теорию двухфазной фильт- рации на течения в анизотропных средах и указать метод проведения и интерпретации экспериментов для определения коэффициентов в тензор- ных связях.

В настоящей работе используется математическая модель двухфазной фильтрации в пористых пластах, сформулированная на основе анализа работ [1-4]:

dp Gm (1 - s]     G IK/c^G c r^c г V с

)-div       pG (VpG-p Ggj| = qG ;(1)

dt           [ ц

5^p ms     Г IK k r _{F F} r^ _F

—--div -F-p (Vp -p g)| = q ;

d t [ ц pG pG = pG (pG) = pG,0 —о", где P° — атмосферное давление;

GV m = m (p ) - пористость (-n- , Vn - объем пор);

s - эффективная влагонасыщенность (0-1);

IK - тензор проницаемости, в общем случае полнозаполненный;

-

s ² ) - относительная проницаемость для газовой фазы;

ц ^G - вязкость газа;

q^G - источниковый член в балансе газовой фазы; q^F - источниковый член в балансе жидкости;

p

k r ^F

= p ^{F ,0} pO- , p ^{F ,0} - плотность флюида при атмосферном давлении;

p ⁰

= W (1 - vi s') - относительная проницаемость для жидкой фа- зы;

ц ^F - вязкость флюида;

V¹ V"

p = p - p ( s ) ; p ( s ) = p --капиллярное давление;

pd - пороговое давление, причем pd =---, где а - параметр, характе- а ризующий пористую среду.

Одномерное приближение

Предельно упростим ситуацию. Примем, что источники отсутствуют, то есть qG=qF=0. Будем рассматривать одномерное движение, в этом слу- r rd       д чае V _ i —, div _ —. Кроме того, примем, что движение происходит в дx       дx горизонтальном направлении: (g)x _ 0. В этом случае уравнения (1) - (2)

можно переписать следующим образом:

др G m ( 1 - s ) _ к KkG , д t         д x _v ц G Р

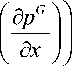
дрFms _ д KkF F дpF д t     дx ^ ц F Р v дx здесь K – коэффициент проницаемости, уже скалярная характеристика.

В уравнениях (3), (4) перейдем к давлениям pG, pF. Для этого заменим ρG и ρF, входящие в левые части этих уравнений, по следующим форму- лам:

G ,0                    F ,0

_G Р__ „о   ^р Р__ pF

Р ^_ —Г Р , Р ^_ —5" Р .

p

p

В результате получим два уравнения следующего вида:

д p^G a G _ д G д p^G ^

д t    д x (   д x /

FF        F дp а _ д р р дp д t    дx (   дx J

G ,0                  F ,0                G ,0 G                   F ,0 F

G /1    \ Р F Р    gG     р kr   G fF Р kF а _ m(1 - s)—5-, а _ ms—г, в _ K——^p , в _ K——Fp , p         p        p ц          p Ц p5 - атмосферное давление, pG,0 - плотность газа при атмосферном давлении, pР,0 - плотность жидкости при атмосферном давлении.

Итерационно-разностный алгоритм

Вернемся теперь к уравнениям (6), (7). Решение этой системы разберем на примере уравнения (6):

д p G a G __дС G д p G ' д t     д x (    д x _v

Построим алгоритм решения этого уравнения с помощью итерационного подхода. Предварительно строим полностью неявную разностную схему для уравнения (9), которая по опыту решения задач теплопроводности и диффузии должна быть абсолютно устойчивой.

Аппроксимируя пространственные производные простейшими разно стями на неравномерной сетке, а производную по времени разностями назад, найдем:

a e P^G G - 1 - a p P^G j + a w P Gl + ^Ь = ⁰,                         ^{( 1 0)}

2 в G - 1                             2 в ^G + 1

где      ae = 7----------77--------V, aw = 7----------77--------г,    (11)

⁽ X + 1 - x j - 1 ⁾⁽ X - x j - 1 )         ⁽ x j + 1 - x j - 1 ⁾⁽ x j + 1 - x j )

a, G     «) n ^{- 1} ( j n ^{- 1}

•

ap = ae + aw + 77, b = "—p            A t             A t

Коэффициенты в этом разностном уравнении определены на новом слое по времени, но с использованием значений на предыдущей итерации.

Выражая из (10) pj, найдем pG

a e p G - 1 + a w p G + 1 + ^Ь

a p

N - 1 ) .

Заметим, что при вычислении источника b необходимо помнить значения величин на предыдущем слое по времени (обозначены верхним индексом n -1).

Расчет с использованием итерационно-разностной технология (ИРТ) нами выполняется следующим образом:

• 1)    задаем начальные распределения давлений (газовой и жидкой фаз) по всей области;

• 2)    с помощью граничных условий вычисляем значения плотностей на концах трубы на новом слое по времени;

• 3)    используя (13), последовательно перевычисляем давление во внутренних узлах расчетной области. Когда перебор точек по индексу закончен, считаем одну глобальную итерацию завершенной;

• 4)    делаем порядка N глобальных итераций. После этого считается за-

• конченным расчет на очередном слое по времени;

• 5)    далее осуществляется переход к новому слою по времени, то есть возвращаемся к пункту 2.

Этот ИРТ-алгоритм (разностная аппроксимация производных, движение по пространственному индексу и последующие глобальные итерации) легко обобщается на плоский случай. При этом формула расчета давления будет выглядеть следующим образом:

p Gk к

^- 1,7 + a w p G + 1, к + a s p G, к - 1 + a n p G к + 1 + ^Ь a p

G           G G n - - 1 / G n - - 1

где   ap = a ⁺ a w ⁺ a_s ⁺ a„ +7 77 , b = —j^ —— ---,         ⁽¹⁵⁾

• p                      A t              A t

а также на пространственный случай

P к , l =

GGGGGG аePj-1,k, l + awPj+1, к, l + asPj, к -1, l + anPj, к+1, l + abPj, к, l -1 + atPj, к, l+1 + Ь

.

а p

Здесь

a = a + a + as + a„ + ab + a, + p ewsn

( a G.>,- ) "" 1

A t

, b =

( a G , „ ) -' ( P G. ) " '

A t

.

При этом a e и a w будут определяться формулами (11), а для a s , a n , a b , a t будем иметь

а

s

2 P G , к—

( У к + 1

Ук - i )( Ук ^- Ук - i )

, a n =7---- ^{( У} к + 1

2 в G 1

к +2

У к - 1 )( У к + 1

- Ук Г

a b = /

( z l + 1

2 в G- 1

z l - 1 )( z l ^- z l - 1 ) , a t ( z l + 1

2P,G i l + zl-1)(zl+1

- zl) "

Здесь у диффузионного коэффициента β для простоты записи целые индексы опущены, а значения этого коэффициента в дробной точке определяются как полусумма значений в целых точках, например, e G =РГ+Р11

.

к - ¹        2

С помощью (16) – (19) можно решать все задачи двухфазной фильтра- ции в однородных анизотропных пластах.

С использованием описанной математической модели были решены тестовые задачи однофазной фильтрации, а также одномерная задача двухфазной фильтрации, а именно, рассчитано течение газожидкостной среды в трубе, заполненной пористым материалом. Кроме этого, получено решение плоских задач двухфазной фильтрации.

Тестирование алгоритма при постоянной насыщенности

Вычисления проводились при следующих значениях определяющих параметров:

L = 6 м – длина трубы;

ρ ^F = 1000 кг/м³; ρ ^{G ,0} = 1,27 кг/м³;

K = 9,869233 ∙ 10–13 м2;

μ ^F = 8,9 ∙ 10^–4 Па∙с; μ ^G = 1,78 ∙ 10^–5 Па∙с.

Далее будем рассматривать движение газожидкостной среды в трубе, заполненной пористым материалом, например, песком ( m = 0,4).

s = 0,8;

s = 0,3;

p^G_ = 10 5 Па.

вых

P Gx _ 1,2 - 10 5 Па;

Рис. 1. Одномерная область двухфазной фильтрации

В случае постоянной насыщенности уравнение для давления газа при- нимает вид квазилинейного уравнения теплопроводности:

dpG _ KkG (s) d

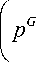
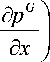
dt ц Gm (1 - s )dx

На рис. 2 представлены результаты решения этого уравнения рассмат- риваемым численным методом. В случае установившегося течения, когда

S p^G

---_ 0, решение легко находится аналитически. На графике аналитиче-д t ское решение практически совпадает с численным, что говорит о корректности применения рассматриваемого численного метода для решения данных уравнений.

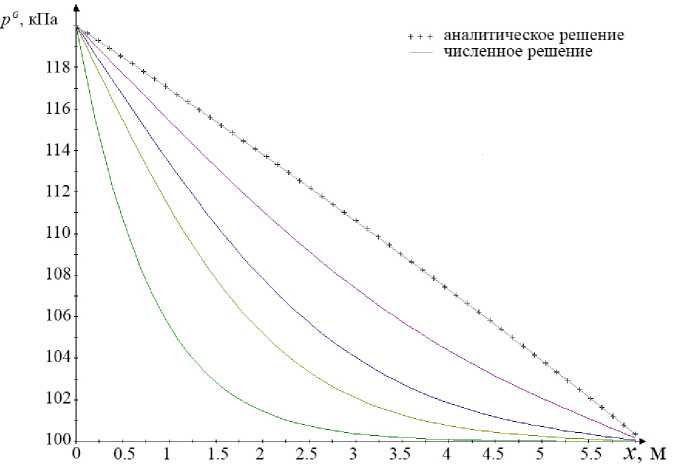
Рис. 2. Распределение давления газа по длине трубы в разные моменты времени

В рассматриваемом примере влага поступает с левого конца трубы за счет скачкообразного увеличения насыщенности в этой части канала от значения s=0,3 до значения s=0,8. Поэтому профиль давления газа, изна- чально имеющий вид «левого нижнего уголка», постепенно деформируется в почти линейное распределение.

Численный эксперимент

При указанных выше параметрах проводился численный эксперимент, отслеживающий динамику развития течения в трубе, заполненной пористым материалом. Были получены распределение давления флюида и газа и распределение насыщенности флюидом пористого пространства с течением времени, представленное на рис. 3. Полученные результаты позволяют анализировать течение и характер заполнения пористого пространства.

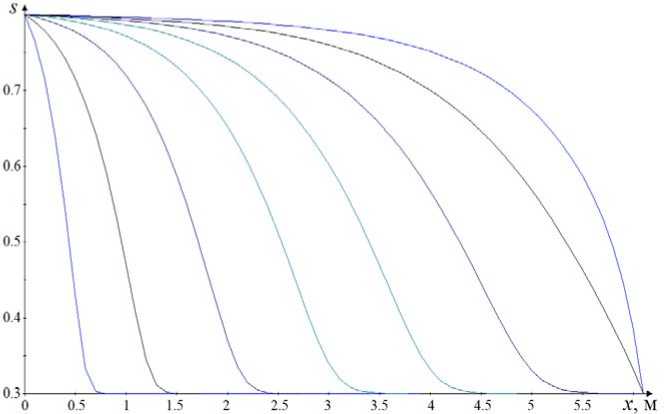
Рис. 3. Распространение волны насыщенности по объему пористого пространства

Как видно из рис. 3, наблюдается волновой механизм распространения насыщенности по пористому пространству трубы. Причем зона изменения насыщенности с течением времени увеличивается. Характерная выпукло-вогнутая форма ее распределения со временем становится более простой и к моменту, определяющему установившееся состояние течения, кривая s = s ( x ) имеет вполне определенный знак кривизны.