Динамика малых возмущений в неравновесном колебательно-возбужденном газе

DOI:

Важным фактором, определяющим физику процессов в химически активных смесях, колебательно-возбужденном газе, неизотермической плазме и средах с неравновесным состоянием фаз [1; 2; 7; 9–11; 15; 20–23; 25; 28], являются дисперсионно-вязкостные свойства неравновесных сред. При определенных условиях в неравновесном колебательно-возбужденном газе звуковые волны оказываются неустойчивыми и среда становится акустически активной. В такой среде за счет релаксационных процессов в колебательно-возбужденном газе вторая объемная вязкость становится отрицательной, что приводит к появлению положительной обратной связи между газодинамическим возмущением и неравновесным тепловыделением (критерий Рэлеевской акустической неустойчивости) [9; 11; 21; 22; 25]. Кроме того, в акустически активном неравновесном газе низкочастотная скорость звука с ₀ может быть больше высокочастотной («замороженной») скорости звука с ^ , что соответствует случаю отрицательной акустической дисперсии [1; 2; 7; 10; 19; 23]. Диссипативная неустойчивость звуковых волн, обусловленная особой моделью турбулентной вязкости, может также возникать как в дифференциально вращающихся газовых дисках вокруг астрофизических объектов (белых карликов, нейтронных звезд, черных дыр, молодых звезд) [13; 17; 18; 27], так и на фронте плоских ударных волн произвольной интенсивности [14].

При изучении динамики линейных волн используется два подхода — временной и пространственный анализ устойчивости. Первый подход основан на нахождении закона дисперсии вида ш(к), где ш — собственная частота колебаний (в общем случае комплексная), а к — заданное вещественное значение волнового числа. В рамках пространственного анализа устойчивости закон дисперсии представляется в виде к(ш) (комплексное к и вещественное ш). Этот подход часто применяется в практических (технических) приложениях, когда требуется определить пространственное усиление или затухание амплитуды акустических волн, генерируемых источником звука. Ранее пространственное усиление звуковых волн в неравновесном колебательно-возбужденном газе рассматривалось в [7; 9; 21; 23] для случая слабой диссипации и постоянных значений мощности нагрева и охлаждения. В рамках этого приближения из рассмотрения исключается важный класс решений дисперсионного уравнения с особыми точками и аномальным законом дисперсии звука. Кроме того, эти приближенные выводы линейной модели применяются далее в нелинейных моделях, основанных на решении общего акустического уравнения с квадратичной нелинейностью [7; 8; 16; 23; 26; 29]. Поэтому актуальной задачей в рамках пространственного анализа устойчивости является исследование динамики малых возмущений в неравновесном газе для общего случая с учетом произвольной вязкости, теплопроводности и различных зависимостей времени релаксации, нагрева и охлаждения от плотности и температуры.

Целью данной работы является исследование дисперсионных свойств акустически активных сред в рамках гидродинамической модели неравновесного колебательновозбужденного газа с учетом вязкости, теплопроводности, нагрева и охлаждения. Основные уравнения математической модели неравновесного газа рассмотрены в п. 1. В п. 2 выводится дисперсионное уравнение, учитывающее зависимости времени релаксации, функций нагрева и охлаждения от термодинамических параметров среды, записываются точные решения для акустического инкремента и скорости звуковых волн, позволяющие детально изучить динамику малых линейных возмущений и определить области аномального поведения дисперсионных кривых, то есть выявить особые точки в законе дисперсии звука.

1.    Математическая модель динамики неравновесного газа

Для описания динамики неравновесных сред рассмотрим простейшую модель однокомпонентного колебательно-возбужденного газа с экспоненциальной релаксацией [7; 23], которая позволяет описывать основные дисперсионно-вязкостные свойства акустически активных сред. Соответствующая система газодинамических уравнений для вязкого теплопроводного газа в одномерном приближении примет вид:

Эд + Э (ди) = 0 Эt Эх

Эди Э dt Эх

( ди ² + р —

Эи д^    = дд,

Эх /

ЭЕ дТ +

Э

Эх

(Е + р)и -

£ — £ е

д ^ Эи ²

2 Эх

ЭТД ав-—

τ

— д1 + дид ,

Э £   Э(£ и)

Эt "*" Эх

£ — £ е

--+ ^{д Q}, τ

где д , р , Т и и — плотность, давление, температура и скорость газа соответственно;

^ = ^- v + ^, v и ^ — коэффициенты первой и второй ди ² соответственно; д — удельная внешняя сила; Е =

кинематической вязкости газа

+

Р

— плотность полной

Y ^— 1

энергии газа без учета колебательных степеней свободы молекул; γ — показатель адиабаты; 8 — плотность колебательной энергии возбужденного неравновесного газа; 8 _е — плотность колебательной энергии газа в равновесном состоянии; τ — время колебательной релаксации; Q и I — функции нагрева (накачки) и охлаждения (теплоотвода) соответственно.

Система уравнений (1)–(4) замыкается уравнением состояния:

Р = RqT,                              (5)

где R = R * /M — газовая постоянная; R * — универсальная газовая постоянная; М — молярная масса газа.

В рассматриваемой модели колебательно-возбужденного газа энергия источника накачки Q идет на возбуждение колебательных степеней свободы и увеличение соответствующей энергии ℰ . При отключении источника накачки колебательная энергия ℰ релаксирует к своему равновесному значению 8 _е , то есть уменьшается по экспоненциальному закону за характерное время τ в соответствии с выбранной моделью релаксации — первое слагаемое в правой части уравнения (4). В процессе релаксации колебательная энергия преобразуется во внутреннюю энергию и приводит к нагреву газу — первое слагаемое в правой части уравнения (3). Для стабилизации нагрева газа и возможности получения стационарных решений в модель вводится функция охлаждения (теплоотвод) I , которая может обеспечивать эффективное охлаждение газа как за счет поперечной теплопроводности, так и посредством высвечивания (излучения) при высоких температурах. Отметим, что при нормальных условиях равновесное значение колебательной энергии газа существенно меньше его внутренней энергии, то есть 8 _е <  p ^{/ (} Y ^- 1) . Выражение для плотности колебательной энергии равновесного газа 8 _е можно записать в виде [23]:

8 е (е-Т ) = — ,^R     , -                          (6)

exp ( 0 /Т) — 1

где θ — характеристическая колебательная температура, зависящая от параметров конкретной смеси газов.

В общем случае величины т, Q и I зависят от термодинамических параметров среды (плотности и температуры). В малой окрестности равновесных значений т ₀ , Q 0 , I 0 , д -- Т 0 функции т (д, Т ) , Q(g, Т ) и I(д, Т ) можно аппроксимировать степенными функциями вида:

т = т о ( i К (ТТ Г ^-Q = Q 0 ( i Г (ТГ ^-           ₍₇₎

I = I 0 ( i Г ( Т г

Зависимости (7) позволяют исследовать динамику звуковых волн в различных акустически активных средах посредством выбора соответствующих параметров т _е , т _т , Q _e , Q t , I _e , I _t . Эти параметры для более сложных не степенных зависимостей величин т (д,Т ) ,

Q ( q,T ) и I ( q,T ) можно определить следующим образом:

а in т е а in Q,	d in т
	т т = d in Т,
d inQ	d inQ
Q e    d in Q, d in I	Q 1 d inT, d in I
e d in q’	T = d inT .

В реальных средах характерное время релаксационных процессов (τ) является сложной функцией температуры. Для конкретных газовых смесей зависимость t ( q,T ) определяется экспериментально и может быть аппроксимирована обобщенной формулой Ландау — Теллера [3; 4; 6; 24], которую представим в виде:

^{т (}Q ^,Т )

Т ^п ехр{ в (Т - 1 / 3 - 1) } τ 0

Q

где Т = Т/Т ₀ , д = q/q ₀ , Т ₀ и q ₀ — начальные стационарные значения параметров газа, а безразмерные параметры в и и могут иметь как положительные, так и отрицательные значения в зависимости от свойств конкретной смеси газов. При фиксированных значениях в формула (9) определяет монотонно убывающие (в > 0 ) и возрастающие (в < 0 ) функции т (Т) . Однако для некоторых газовых смесей и при расширении температурного диапазона функция т (Т) имеет явно немонотонный характер [3; 4]. Например, для га-логеноводородов при Т < Т * ~ 700-900 K величина т возрастает с ростом температуры, а в случае Т > Т * , наоборот, убывает (см.: [4, с. 662]). Таким образом, в общем случае параметр β должен быть функцией температуры в формуле (9).

Важной характеристикой неравновесных сред, влияющей на динамику акустической неустойчивости, является в первую очередь зависимость времени колебательной релаксации от температуры, которая в соответствии с (8) определяется значением параметра т _т . С учетом (9) для т _т при в = const получим:

т т (Т ) = и - ^в Т ^-1/3 + Т& (т ^-1/3 — 1 ) . 3           d!

В данной работе в качестве модельной акустически активной среды, для которой соотношение (9) справедливо в диапазоне температур (300–3000 K) [3; 4], рассмотрим типичную газовую среду CO ₂ -лазеров с объемными долями компонент CO ₂ : N ₂ : He = = 1:2:3 . При нормальных условиях ( р ₀ = 1 атм, Т ₀ = 300 K) для параметров такой смеси газов в соответствии с [23] имеем т ₀ « 10 ^-5 с, т _т « — 3,4 , т _е = — 1 , у ~ 1,46 , 0 ~ 3600 K, в ~ 8, 7 , Q o ~ 0, 76 кг/м ³ , с ^ = V Y P ₀ /Q 0 ~ 441 м/с и R « 445 Дж/(кг - К).

2.    Динамика малых возмущений в неравновесном газе2.1.    Линеаризованные уравнения и закон дисперсии

Проведем стандартную процедуру линеаризации системы уравнений (1)–(4), то есть представим все величины в виде / = /0 + / и ограничимся только линейными по возмущениям / слагаемыми. В качестве начального стационарного состояния рассмотрим однородную покоящуюся среду (Q0, ро, Ео, 8о, 8ео, Qo, 1о, то = const, ио = 0) в отсутствии внешних сил (д = 0). Решение полученных таким образом линеаризованных уравнений будем искать в рамках ВКБ-приближения, представляя возмущенные величины в виде плоских гармонических волн /(t,x) = /(ш, к) exp{ —iшt + ikx} с частотой ш и волновым числом к. В результате такой подстановки линеаризованные уравнения в частных производных относительно возмущенных величин сведутся к системе линейных алгебраических уравнений (СЛАУ) относительно их комплексных амплитуд /:

— i w g + ikQ ₀ и = 0 ,

Р г ,2-

— i ш и = —ik-- t к и,

Q o

—. ш Е + ik(E ₀ + р ₀ )и + к^ а еТ =

8 — 8 е

τ 0

— Q ₀ Q ₀f 1 + 1 + Е

\ ^т0    ^Q 0    к о

—. ш 8 + ik8 ₀ и =

8-8 е

-

τ 0

+ ^Q 0 ^Q 0

(

"+^+

Т о     Q o

Q

Q o    ’

При выводе линеаризованных уравнений (13)–(14) использовались стационарные решения 8 _о — 8_{е 0} = т ₀ Q ₀ Q ₀ и Q _o = 1 _о , обеспечивающие начальное равновесие системы.

В рамках линейного анализа устойчивости возмущение произвольной функции ф (Q, Т ) можно представить в виде:

Ф ( q,t ) = ?(^) + Т Г | ф ) .                     (15)

9q /о       9^Т /о

Дополнительные соотношения между возмущенными величинами, необходимые для разрешения системы уравнений (11)–(14), можно получить с учетом выражений (5)–(8) и (15):

о     о    о    пл

_Е = Р   ^Р = ^Q ₊ Т

^{Y —} 1 ,   Р о     ^Q 0 ^Т 0 ,

О         ГП             О      ГП

_ с ^{Q        Т    Т   Q} I ^Т

⁸ е = ⁸ ео-- + ^р о С е ^ , ” = ^{Т е} --^{+ Т т} Т",                  ⁽¹⁶⁾

О        ^{о           о      о}       ,^{о         о}

^Q = Q . ^ + Q t ^Т, 1 = / ,   + 1 т ^Т

^Q o        Q o        ^Т о ^к о      Q o       ^Т о

1 / 98 \ где е   QoR\.aт )0

Из первых двух уравнений (11) и (12) линеаризованной системы легко получить:

ш ( ю + . t к ² )    =         ,                          (17)

Qo     Y Ро где с^ = VYRT0 — высокочастотная «замороженная» скорость звука, соответствующая скорости звука в невозбужденном (равновесном) газе. Проводя несложные преобразования уравнений (13) и (14) с учетом (16) и (11), получим:

Y |              ₍₁ - ^ ^т о ) ₊

⁺ [С _е ⁺ S("Ту ^{— т} д ^{+ 1} Т ^— 1 д)\ ~ ⁺

+ г     (Qg — QT — 1д + 1Т)1

YWTo

=

^{ш +} J^X^ (1 — г шт о ) + [С _е + S( т т + I t )] Y i +

,•YiS

+г----(1Т — qt )

што           Ро где х =--коэффициент температуропроводности; су — удельная теплоемкость при QoCy постоянном объеме; Y1 = Y — 1; S = —--безразмерная величина, характеризующая RTo степень неравновесности среды.

Приравнивая определитель системы уравнений (17)–(18) к нулю и вводя безраз-^      X        _ _ мерные величины ш = шт0, к = ктос^, ^ = ——, х = —^~, получим искомое тосоо         тосоо дисперсионное уравнение для акустически активной среды в модели неравновесного колебательно-возбужденного газа с учетом вязкости и теплопроводности:

си( ш + г£,к 2 ) [ (с и + гхк 2 )(1 — г ш ) + шА 1 + гВ^ = = к ² [ (cv + z (;y /y )^ ² )(1 — геи) + (ША 2 + гВ 2 ] ,

где

^А 1 = ^Y i ^[C _e ^{+ S ( т} т ^{+ 1} т ^)],

^А 2 = ~^[^ е ^{+ S ( т} Т ^{— т} д ^{+ 1} Т ^{— 1} д ^)], ^γ

^В 1 = ^Y 1 ^{S ( I} t ^{— q} t ),

^В 2 =    ^S(Q g ^{— Q} T ^{— 1} д ^{+ 1} Т )•

γ

В общем случае полученное дисперсионное уравнение описывает четыре моды колебаний — две звуковые и две энтропийные (вихревую и тепловую). Для невозбужденного ( А ₁ , 2 = В ₁ , ₂ = 0 ) газа в бездиссипативном пределе (^ = х = 0 ) дисперсионное уравнение (19) имеет три корня — ш ₁ , ₂ = ±кс ^ (две звуковые ветви колебаний) и ш = 0 (энтропийная мода).

Дисперсионное уравнение (19) можно использовать как при решении задачи на нахождение собственной частоты колебаний ω, так и на определение собственного значения волнового числа к. В первом случае получаем закон дисперсии вида ш(к), то есть определяем комплексную частоту по заданному вещественному значению волнового числа. Второй вариант соответствует закону дисперсии вида к(ш), при котором определяется комплексное волновое число (к = Re к + г Im к) по заданному вещественному значению частоты. В практических приложениях чаще всего требуется определить, как изменяется амплитуда волн в зависимости от расстояния до источника, который их и генерирует. Поэтому здесь будем рассматривать второй вариант закона дисперсии к(и) и для облегчения дальнейшего анализа представим (19) в виде уравнения с явным выделением степеней искомого волнового числа к:

* К^к+Y)^{+ г} (Y

+ {cd [1 + Л 2 + ЗВ— —

® чШ⁴+ ^{d 2} (х + D] +

—

+ г [ ^З 2 ^— со ^{2 (1} + х + ⁽1 + Л — )^) ]} к^{2 —}

— си ² [с и (1 + Л _— ) + г(З _— — си ² ) ] = 0.

Полученное уравнение является биквадратным и имеет в общем случае четыре аналитических решения для звуковых и энтропийной мод колебаний.

Ограничимся сначала рассмотрением случая х = 0 , при котором уравнение (20) описывает только две звуковые ветви колебаний и имеет решение:

— / 2     । - +^а + V ^a 2 + ^b 2

к = ± d [а + гЬ] ¹ = ±шМ -----------±

/ ^— а + V ^a 2 + ^b 2

±г ш sign(b) у-------^-------, где

а — {си ² (1 + Л — )[1 + Л 2 + ^к(З — — си ² )] +

+ (З— — СС)2)[З2 — d2(1 + (1 + Л—)к)]} /d, b = си {си2(Л— — Л2) + (1 + Л2)З— — (1 + Л—)З2 + + к [(З— — d2)2 + d2(1 + Л—)2]} /d, d — си 2[1 + Л2 + к(З— — си2)]2 + + [З2 — СО2 (1 + (1 + Л—)к)]2.

При определенных значениях параметров т _е , т _т , Q _e , Q _T , I _e , I _T и степени нерав-новесности среды S в (21) появляются решения с акустическим инкрементом а = = — Im к >  0 , характеризующим скорость роста амплитуды неустойчивых звуковых волн /(t, ж) a i ^A' " X ' ⁽' - ' ' ^{Re k} , где _Cs = —_ — фазовая скорость волны. Введем безразмерные c _s акустический инкремент а = ат ₀ с ^ и фазовую скорость c _s = — . ^с ^

В качестве базовых значений безразмерных параметров y, те и тт выберем значения, соответствующие модельной газовой среде CO2-лазеров (см. п. 2 и [7; 23]). Для величины вязкости примем = 10-5, а с учетом соотношения (6) безразмерный параметр Се ~ 8, 36 х 10-4. Базовые значения параметров источника накачки и теплоотвода определим следующим образом: S = 0,1, Qe = QT = Ie = IT = 0. Далее, если явно не указаны значения параметров модели, то принимаются их базовые значения.

На рисунках 1–2 показаны дисперсионные кривые, соответствующие решению (21), для различных значений степени неравновесности среды S, вязкости ^ и функциональных зависимостей t(q,T), I(д,Т), Q(q,T). Как видно из рисунка 1a, инкремент акустической неустойчивости в низкочастотной области си < 1 быстро возрастает с увеличением частоты (а си2), а в окрестности значений си ~ 10 достигает своего максимального значения а max. В области высоких частот си ~ 100 происходит стабилизация неустойчивости за счет вязкой диссипации энергии звуковых волн (случай I, > 0), а в бездиссипа-тивном пределе (случай 1 = 0) величина а max практически не изменяется при си ^ то и асимптотически стремится к аю ~ аmax. Фазовая скорость неустойчивых звуковых волн убывает с увеличением частоты, что соответствует отрицательной акустической дисперсии (рис. 1b), и практически не зависит от вязкости среды (ξ). С увеличением степени неравновесности среды S возрастает как акустический инкремент (а), так и низкочастотная скорость звука (с0 = — = lim cs).

'\ ^ш - °

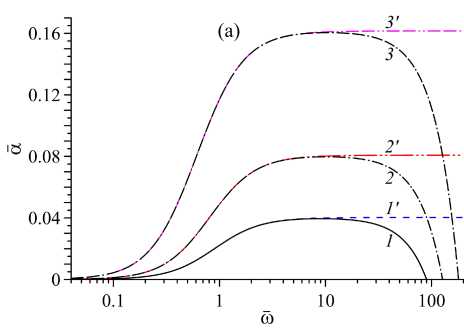
Рис. 1. Зависимости акустического инкремента а ( a ) и фазовой скорости звуковых волн c _s ( b ) от частоты (V при различных значениях S и ^ :

( 1-1’ ) — S = 0 , 1, а= 10 ^-5 — 0; ( 2—2’ ) — S = 0 , 2, а = 10 ^-5 - 0;

( 3-3’ ) — s = 0 , 4, а = 10 ^-5 - 0

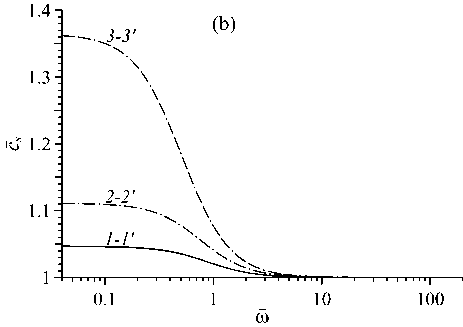
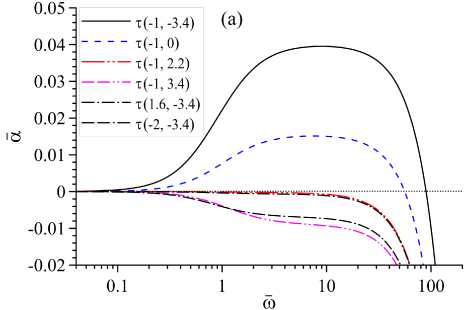
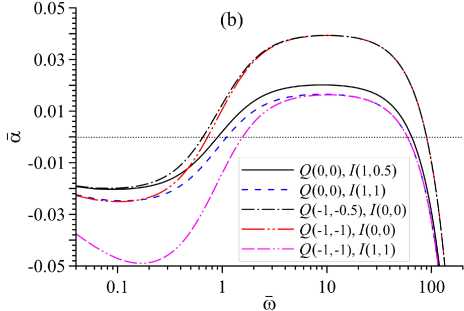
Рис. 2. Зависимость акустического инкремента а от частоты ш в различных моделях: ( a ) — времени релаксации т ( т _е , т _т ); ( b ) — нагрева Q(Q _g ,Q _t ) и охлаждения I(I _e , I _t )

Влияние параметров моделей релаксации (тв, тт), нагрева (Qe,QT) и охлаждения (1 в, 1т) на акустический инкремент показано на рисунке 2. Как видно из рисунка 2a, с увеличением параметров тв, тт величина а уменьшается, и при значениях тв > 1,6, тт > 2.2 становится отрицательной, то есть происходит стабилизация неустойчивости и звуковые волны затухают за счет вязкой диссипации. В случае Qe = QT = 1в = 1т = 0 акустический инкремент является монотонной функцией частоты в области ш < 1. Отличные от нуля значения параметров моделей нагрева и охлаждения оказывают сильное влияние на величину а, в первую очередь в низкочастотной области, и приводят к на- рушению условия монотонности в окрестности 0 < си < 1. Как видно из рисунка 2b, акустический инкремент убывает с увеличением параметров Iq, It и с уменьшением Qq, Qt, причем функция а(си) является немонотонной и знакопеременной. Для параметров модели, представленных на рисунке 2b, в низкочастотной области (си < 0, 3) звук затухает с декрементом —О ~ 0,02-0,05, а в окрестности си ~ 10 звуковые волны нарастают с инкрементом О ~ 0, 01-0,04.

2.2.    Критерий устойчивости

В работах [7; 23] для акустически активной среды, описываемой дисперсионным уравнением (20) при ^ = х = I _q,_T = Q _q,_T = 0 , на основе приближения | Re k | ^ ^ | Im k | были определены четыре характерные области неравновесности в зависимости от величины S :

• I.    Область с положительными акустической дисперсией и второй вязкостью ( 0 < S <  <   S i ). В данной области, как и в невозбужденной равновесной среде с вязкостью, звуковые волны затухают.

• II.    Область с отрицательными акустической дисперсией и второй вязкостью ( S _i <  < S <  S _ii ). Здесь звуковые волны неустойчивы (Im к <  0 ). Причем при S ^ S _ii низкочастотная скорость звука с ₀ существенно превышает высокочастотную с ^ («замороженную»).

• III.    Область с положительной дисперсией и отрицательной второй вязкостью ( S _ii < < S <  S _iii ). В этой области низкочастотный звук распространяться не может, поскольку в соответствии с [7; 23] с 0 < 0 .

• IV.    Область с положительной дисперсией и отрицательной объемной вязкостью ( S _iii < S ). В данной области наряду с акустической неустойчивостью возможна также и тепловая неустойчивость.

Выведем сначала выражение для величины Si в общем случае Iq,t = 0, Q6,t = 0. Переходя в (21) к пределу си ^ то при | = 0 и учитывая, что в данном пределе а ^ 1 и b ~ — (А1 — А2), получим выражение для высокочастотного акустического инкремента: ω о го

СО ^CU)    ^А 2 ^— А 1

= — lim Im к(ш) = — lim -----=------= си ^го                си ^ГО    2           2

= ^— ~ { Y i Ce + ^S [ ^y i ^(t t + I t ) + ^t q + ^I q ^]} .

2 y

Из полученного выражения следует, что О ^ и, как следствие, О _max линейно возрастают с увеличением степени неравновесности среды S .

Искомую величину S _i можно найти из уравнения О ^ (S _i ) = 0 . В результате с учетом (22) будем иметь:

S i =

Y i C e

Y i ^{( — t} t ^— I t ) ^{— t} q ^— I q

В предельном случае I _q,_t = 0 выражение (23) соответствует величине S _i , полученной в работах [7; 23]. С увеличением значений параметров t _q,_t , I _q,_t возрастает и величина S _i . Так, например, для базовой модели имеем S _i ~ 1, 5 х 10 ^-4 , а если положить I _q = 1 и I _t = 0, 5 , то получим S _i ~ 2, 9 х 10 ^-4 .

Поскольку по определению С _е >  0 , то положительное значение S i в (23) можно получить только при выполнении условия y ₁ ( — т _т — 1 т ) - т _е — 7 _е > 0 , которое позволяет определить критическое значение т _т * как функцию параметров т _е , 7 _е и 1 _т :

* _ ^т т =

^т е ⁺ ^ е

-

Y 1

— 1т .

При т _т <  т т звуковые волны могут быть неустойчивы в случае S > S _i , а для т _т >  т т акустическая неустойчивость не возникает при любых сколь угодно больших значениях неравновесности среды S . Так, например, для базовой модели имеем т т ~ 2,17 , а если положить 1 _е = 1 и 1 _т = 0, 5 , то получим т т = — 0, 5 .

Из соотношений (22) и (23) следует, что величины а ^ и S _i не зависят от параметров Q _e ;r , определяющих зависимость источника накачки (нагрева) от плотности и температуры. Это объясняет поведение дисперсионных кривых а(си) при Q _e ,T = 0 на рисунке 2b, из которого видно, что параметры Q _e ;r влияют на акустический инкремент только в низкочастотной области спектра, а для высокочастотного звука их вклад сводится к нулю.

Определим теперь величины S _ii и S _iii , проанализировав функциональные зависимости Re к( й Ь) и c _s (cu) . Для этого представим выражение для квадрата фазовой скорости звуковых волн с учетом (21) в виде:

; 2 _   си2   _ 12

^s     ( Re ^c) ²     | a | sign (a) + V 1 + b ² /a ²

Рассмотрим сначала случай 1 _е , _т = Q _e ,T = 0 ( В ₁ = В ₂ = 0 ), тогда в низкочастотном пределе си ^ 0 будем иметь:

lim a(co) = an = ———1,     lim b(cv) = bn= 0 ,

ей ^0 V 7     °    1 + A2       й ^0 v 7     0’ а для квадрата низкочастотной скорости звука из (25) c учетом (26) получим:

^c o ²

| a ° | [ sign (a o ) + 1] ^.

Из соотношений (21), (25)-(27) следует, что величины S _II и S iii , соответствующие при си = 0 особым точкам функций c _s (S) и Re k(S ) , можно определить из уравнений 1 + A ₁ (S _ii ) = 0 и 1 + A ₂ (S _iii ) = 0 . В результате получим:

S ii =

¹ + ^Y 1 ^C e

— Y 1 Т т ,

S iii

Y + Y 1 C e Y i ( T e — Т т ).

Выражения для величин S _ii и S _iii в (28) соответствуют определенным ранее в работах [7; 23]. Из соотношений (26) и (28) следует, что при S < S _ii или S >  S _iii величина a ₀ положительна, а в области S Е [S _ii , S iii ) имеем a ₀ <  0 . Кроме того, в случае a ₀ <  0 знаменатель в (27) обращается в ноль, то есть с 0 = то . Таким образом, для низкочастотной скорости звука в пределе си ^ 0 с учетом (27)-(28) получим:

С ²

1 + А 2

*   1 + Ai то,

S < S ii или S >  S iii ;

S ii iii .

Из (29) следует, что при S = Sm (то есть при 1 + А 2 = 0 ) с 02 = 0 , а в остальных случаях величина с 02 всегда имеет положительное значение < то . В работе [7] было показано, что в области III ( Su < S <  Вш ) величина с 0 оказывается отрицательной и на этом основании сделан вывод о невозможности распространения звуковых волн в низкочастотной области спектра (со ^ 1 ). Однако этот вывод противоречит полученному нами соотношению (29) и дисперсионным кривым на рисунке 3a, демонстрирующим зависимости фазовой скорости звуковых волн от частоты при различных значениях S . Различия в оценках величины с 02 связаны с тем, что в [7; 23] вместо соотношения (27) использовалось выражение с 2 = а -¹ , которое получено в приближении | Re к | ^ | Im к | и приводит в случае а ₀ < 0 к отрицательным значениям квадрата низкочастотной скорости звука.

Как видно из рисунка 3a, для акустических гармоник с ш < 1 закон дисперсии с ₈ ( ш ) сильно зависит от степени неравновесности среды ( S ). При S < 8ц имеем отрицательную акустическую дисперсию ( с ₀ > с ^ ) с конечным значением низкочастотной скорости звука ( с ₀ <  то ). В области S Е [Su,3т ) фазовая скорость звука быстро возрастает с уменьшением частоты, стремясь при о ^ 0 к бесконечности, что также соответствует отрицательной акустической дисперсии. Для случая S >  Su i получаем положительную акустическую дисперсию ( с ₀ < с ^ ), а значение низкочастотной скоро- т т — т ₀

сти звука изменяется от нуля при S = Вш до с ₀ =----- - с _то ~ 0,48 с _х при S ^ то и

YTt базовых значений параметров.

Из поведения дисперсионных кривых на рисунке 3a следует, что при о < 10 ^-2 зависимость вещественной части волнового числа от частоты имеет степенной вид Re к к о ² , где величина г является функцией S . Так, в областях II и IV ( S <  S _ii и S >  Вш ) имеем г ~ 1 , при S = S _ii — г ~ 1, 5 , в области III ( Su < S <  Вш ) — г ~ 2 , а в случае S = Вш — г ~ 0, 5 .

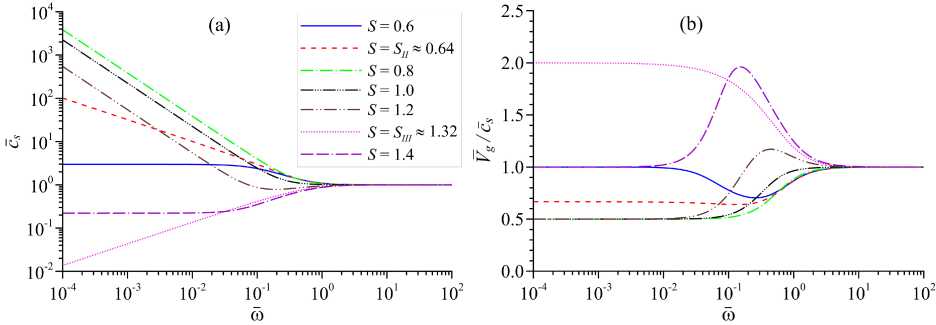
Рис. 3. Зависимость скорости распространения звуковых волн в акустически активной среде от частоты о при различных значениях S: (a) — фазовая скорость cs;

д Re fc у д ш /

-1

( b ) — отношение групповой скорости V _g =

к c _s

с

На рисунке 3b показаны зависимости от частоты групповой скорости звука V _g =

_ к д Re к у д ш )

-

по отношению к фазовой c _s , из которых также видно, что для акусти-

ческих гармоник с со <  1 поведение дисперсионных кривых сильно зависит от степени неравновесности среды. Так, при S <  8ц и S >  Вш групповая скорость совпадает с фазовой для низких (с < 10 ^-2 ) и высоких (со > 10 ) частот звукового спектра, а в области между этими частотами зависимость отношения -^ от (<й ) имеет немонотонный харак- ^ 8

тер с минимумом « 0, 75 для S < 8ц и максимумом « 2 для S > Вш . При S = 8ш и S Е [S _II ,S _III ) групповая скорость также совпадает с фазовой для высоких частот (с о > 10 ), а в низкочастотной области (со < 10 ^-2 ) получаем V _g ~ 2 с ₈ при S = Su i и V g « 0, 5 с ₈ при S ii < Siii.

Таким образом, полученные результаты свидетельствуют о том, что степень нерав-новесности колебательно-возбужденного газа S оказывает существенное влияние на закон дисперсии звуковых волн. При этом для акустически активной среды можно выделить три характерные области (II, III и IV), представленные на рисунке 4, в которых закон дисперсии неустойчивых звуковых волн качественно различается в низкочастотной области спектра. На рисунке 4, помимо с ₀ (S) , также показаны зависимости фазовой скорости звука с ₈ от S при различных значениях со = (10 —⁴ , 10 ^-3 , 10 ^-2 ) из низкочастотной области спектра, демонстрирующие эффекты быстрого возрастания скорости распространения возмущений до значений, на несколько порядков превышающих высокочастотную скорость звука с _ю при переходе из области II в область III, а также последующего уменьшения величины с ₈ при приближении к области IV. Для наглядности на этом же рисунке показана зависимость от S максимально возможного акустического инкремента а ^ , позволяющая оценить скорость роста возмущений при различных значениях степени неравновесности газа и заданных параметрах базовой модели. Из рисунка 4 нетрудно определить следующую зависимость а ^ (S) ~ 0,4S .

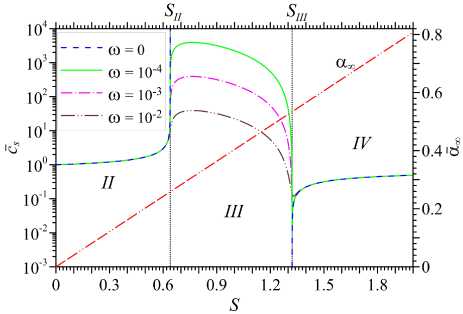
Рис. 4. Зависимость низкочастотной скорости звука от степени неравновесности акустически активной среды S при различных значениях частоты со.

Показана также зависимость а ^ ( S ) (значения на правой оси У )

Рассмотрим теперь случай, при котором коэффициенты В 1 и В ₂ в соотношении (21) не обращаются в ноль одновременно, что соответствует 1 _е , _т = 0 и Q _eT = 0 . В результате для а ₀ получим:

lim а(с о ) = ап = ей -о ⁴

В 1

В 2

1 т — Q t

^Q q ^{— q} t ^— ! д + 1 т

Значения величин Ь _о и с 02 определяются аналогично предыдущему случаю ( 1 _е , _т = Q _e , _T =

= 0 ). С учетом соотношений (26), (27) и (30) выражение для с 0 примет вид:

^с 0

В 2

B i го ,

1 ^Q g - ^Q T - ^I g + I t

Y      I t - ^q t

a ₀ >  0

a ₀ <  0.

Из (31) следует, что значение низкочастотной скорости звука (с0) не зависит от S. Таким образом, учет зависимости функций нагрева и охлаждения от термодинамических параметров приводит к вырождению (исчезновению) границ Su и Siu между областями, в которых закон дисперсии звуковых волн качественно различается. Однако, как видно из соотношения (31), низкочастотная скорость звука может принимать три характерных значения, определяющих качественно различные законы дисперсии звуковых волн, в зависимости от величины а0 и параметров Ig,T, Qg,T: 1) с0 = 0; 2) 0 < с0 < го; 3) с0 = = го. Эти три предельных значения с0 можно получить, например, в рамках следующих моделей c Qg,T = 0 и различными значениями Ig,T: 1) Ig = 1, It = 1; 2) Ig = 1, It = 1, 5; 3) Ig = 1, It = 0, 5 — модель свободно-свободного тормозного излучения. На рисунках 5–7 для этих трех моделей показаны зависимости от частоты фазовой скорости звуковых волн при различных значениях степени неравновесности газа (S). Из поведения дисперсионных кривых в низкочастотной области спектра следует, что, как и в предыдущем случае, зависимость вещественной части волнового числа от частоты имеет степенной вид Re к а соz, где величина г зависит от выбора модели: 1) г ~ 0, 5; 2) г = 1; 3) г « 2;

Как видно из рисунков 5–7, для всех трех моделей при определенных значениях S на дисперсионных кривых в области средних частот (со ~ 1 ) имеется особенность, в которой фазовая скорость звука обращается в бесконечность. Обозначим эту особую точку звукового спектра как со * , значение которой зависит от S и выбора модели охлаждения I _g , _T .

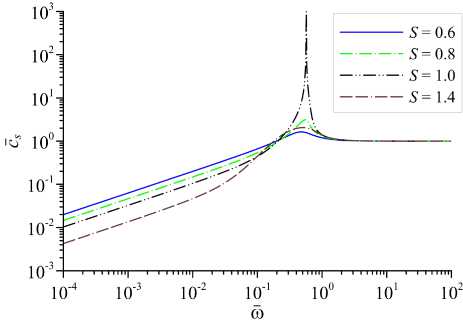
Рис. 5. Зависимость скорости распространения звуковых волн в акустически активной среде от частоты со при различных значениях S для модели 1 (1 _е = 1, 1 _Т = 1)

Анализ выражения (21) показывает, что при со = со * вещественная и мнимая части волнового числа обращаются в ноль, а закон дисперсии звуковых волн в окрестности особой точки со * становится аномальным. В качестве примера аномального поведения дисперсионных кривых на рисунке 8 показаны зависимости вещественной и мнимой части волнового числа от частоты для модели 3. В области частот со < со * звуковые волны затухают, а закон дисперсии в окрестности особой точки ( 0, 2 < <о < со * )

становится аномальным, так как здесь групповая скорость оказывается отрицательной (Re к а 1/ й). При си >  со * звуковые волны становятся неустойчивыми и нарастают с акустическим инкрементом а ( й ) , имеющим вблизи особой точки ей * хорошо выраженный максимум, превышающий значение а ^ , а групповая скорость положительна, и в окрестности ей * может существенно превосходить фазовую. Функция V g (ей ) в особой точке имеет разрыв второго рода: _ lim V _g ( й ) = —то , _ lim V _g ( й ) = + то .

си ——ей * —0 си ——ей * +0

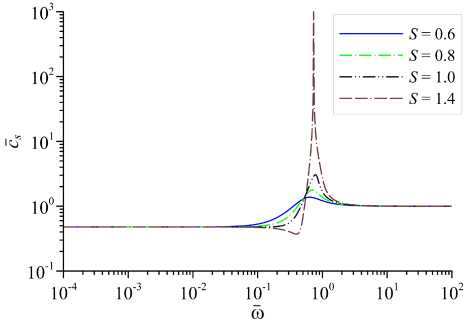
Рис. 6. Зависимость скорости распространения звуковых волн в акустически активной среде от частоты й при различных значениях S для модели 2 (I _е = 1, 1 _Т = 1 , 5)

со

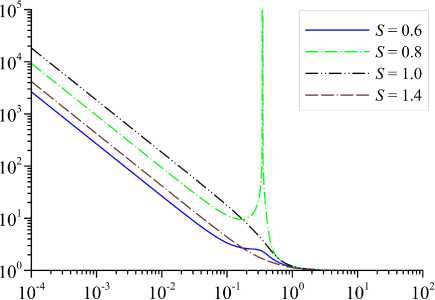
Рис. 7. Зависимость скорости распространения звуковых волн в акустически активной среде от частоты й при различных значениях S для модели 3 (1 _е = 1, 1 _Т = 0 , 5)

Значение й * определяется из совместного решения системы уравнений: Re к (ей) = = 0 и Im к (ей) = 0. Поскольку величина й* является корнем сразу двух уравнений, то это накладывает ограничения на диапазон значений S (S* < S < S*h), при которых могут появляться решения с особыми точками в соответствующем диапазоне частот й* < й* < ей*^. Как граничные значения диапазонов (S*l,S*h) и (ей*, й*^), так и сама функция й*(S) зависят от выбора модели охлаждения. На рисунке 9 показана зависимость ей * (S) для различных моделей охлаждения I (Ie Дт), крестиками на рисунке отмечены границы диапазонов частот и степени неравновесности среды. Как видно из этого рисунка, функция й*(S) является монотонно убывающей, а сами диапазоны смещаются в область больших значений с увеличением параметра 1Т. Кроме того, при значениях 1Т > 1 происходит резкое увеличение значения со* и диапазон аномальных частот смещается ближе к окрестности со ~ 1.

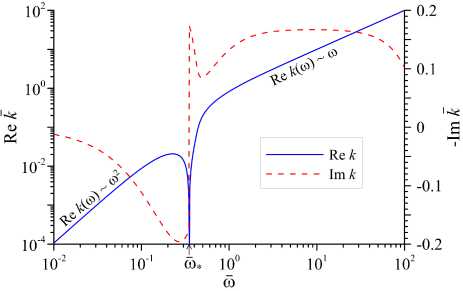
Рис. 8. Зависимость вещественной и мнимой части волнового числа к от частоты си для модели 3 (I _Q = 1, 1 _Т = 0 , 5) при S = 0 , 8

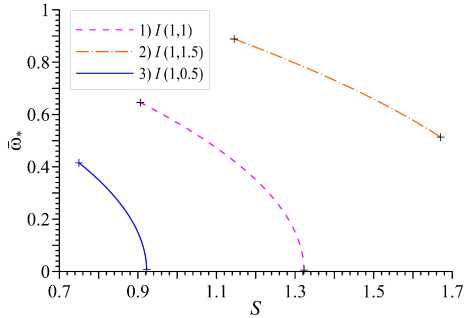
Рис. 9. Зависимость частоты со * от степени неравновесности акустически активной среды S для различных моделей I(I _Q ,1 _Т )

Отметим, что аномально высокое значения скорости звука (в особых точках равное ∞ ), получаемое как в низкочастотном пределе, так и в области средних частот (си ~ 1 ) при достаточно больших значениях степени неравновесности среды, по-видимому, является следствием используемой модели (однокомпонентный неравновесный колебательно-возбужденный газ и линейное приближение). Однако даже с учетом взаимодействия различных молекул газовой смеси в многокомпонентных моделях [12] и нелинейных поправок скорость звука в окрестности особых точек хотя и будет меньше ∞ , но, скорее всего, останется аномально высокой, что может существенно повлиять на динамику физических процессов, протекающих в акустически активных средах. Кроме того, знание закона дисперсии звуковых волн в неравновесном колебательно-возбужденном газе, в особенности с аномальным поведением дисперсионных кривых, имеет важное практическое значение при построении устойчивых численных схем для нелинейного газодинамического моделирования.

2.3.    Влияние вязкости и теплопроводности

Рассмотрим сначала предел невозбужденного равновесного газа ( Л 1 , 2 — В 1 , 2 — 0 ) с учетом вязкости (^ > 0 ) и теплопроводности ( % > 0 ). Так как в реальных газах при нормальных условиях для диссипативных коэффициентов выполняются условия ^ ^ 1 и % ^ 1 , то полагаем влияние диссипации на звук малым: к — си + Ё, где Ё ^ со — безразмерная диссипативная поправка. Разрешая уравнение (20) относительно ё в линейном приближении по диссипативным коэффициентам (^ , % ) и Ё, получим хорошо известное выражение для диссипативной поправки к закону дисперсии звуковых волн [5]:

Ё - 4 h % ( 1 -Y^ (32)

Из (32) следует, что звуковые волны в вязкой теплопроводной среде затухают с декрементом -ё а — о ² .

Сравнивая теперь (32) и выражение для акустического инкремента (22), найдем значение критической частоты (си ,.,.,/ ), при которой вязкость и теплопроводность полностью подавляют неустойчивость звуковых волн в неравновесном акустически активном газе. Разрешая уравнение — - а ^ + Ё ( й ) crit ) — 0 относительно со _crjt , получим:

^и сгИ

α _∞

■                                       ■

Отметим, что в рассматриваемом приближении малой диссипации, учет вязкости и теплопроводности в дисперсионном уравнении (19) практически не оказывает заметного влияния на закон дисперсии звуковых волн Re к ( о ) в неравновесном колебательно-возбужденном газе и аномальное поведение дисперсионных кривых в окрестности особых точек. Как видно из соотношений (32) и (33), влияние диссипативных факторов сводится лишь к уменьшению акустического инкремента в области высоких частот со ^ 1 , приводя к подавлению неустойчивости звуковых волн при о >  со _стц .

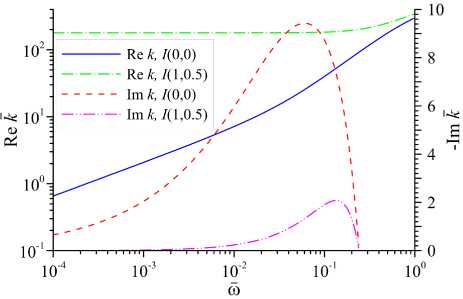
Рис. 10. Тепловая неустойчивость. Представлены зависимости волнового числа от частоты ш для различных моделей I(I _e ,I _T ) при S = 1 , 4 и % = 10 ^-5 для различных моделей I(1 _е ,I _T )

Как отмечалось ранее в п. 2.2, при достаточно больших значениях степени нерав-новесности среды (S > 8ш) в колебательно-возбужденном газе возникают условия для появления тепловой неустойчивости. Из решения дисперсионного уравнения (20) при К > 0 и X > 0 следует, что помимо двух звуковых ветвей колебаний, подробно рассмотренных выше, имеются еще две моды — вихревая и энтропийная. Вихревая мода при любых значениях параметров S является затухающей (Im к > 0), а амплитуда энтропийной моды в области IV (S > Sin) нарастает (Im к < 0) и соответствует тепловой неустойчивости неравновесного газа. На рисунке 10 показаны зависимости вещественной и мнимой части волнового числа энтропийной моды от частоты для различных моделей охлаждения. Как видно из этого рисунка, тепловая неустойчивость локализована в области сравнительно низких частот (си < 1), а ее инкремент почти на порядок превышает акустический при заданном значении параметра S. Скорость распространения наиболее неустойчивых энтропийных возмущений на несколько порядков меньше скорости звука и составляет ~ 10-3-10-2с^.

Заключение

На основе линейного анализа устойчивости (п. 2) показано, что динамика неустойчивых звуковых волн сильно зависит от степени неравновесности среды S (интенсивности нагрева) и параметров (степеней) функциональных зависимостей т ( р ,Т ) а g^{T p} Т ^{Т т} , Q( p ,T ) а ^Т ° ^т и I( р ,Т ) а y ^{i p} Т ^{1 т} . С увеличением параметров S , Q _e , Q _t и уменьшением т _е , т _т , I _e , I _t акустический инкремент а возрастает. В моделях нагрева ( Q _e <  0 , Q _t <  0 ) и охлаждения ( I _e >  0 , I _t >  0 ) дисперсионные кривые имеют немонотонный характер — в области частот шт < 1 звуковые волны затухают (а < 0 ), а при шт > 1 могут быть неустойчивыми (а > 0 ). Кроме того, параметры Q _e и Q _t оказывают влияние только на звуковые гармоники с частотой шт < 1 , приводя либо к затуханию этих гармоник, либо к увеличению инкремента неустойчивости в этой области спектра.

Для моделей с постоянными значениями нагрева и охлаждения ( Q ( q, Т ) = const и I(д,Т ) = const ) определены четыре области неравновесности, зависящие от величины S с границами S _i , S _ii и S _iii . Акустические волны в первой области ( 0 <  S < S _i ) характеризуются положительной дисперсией, то есть низкочастотная скорость звука меньше высокочастотной ( с ₀ <  с ^ ), и являются затухающими. В остальных областях (II-IV) при S > S _i звуковые волны становятся неустойчивыми, а значение их максимального инкремента линейным образом зависит от степени неравновесности среды (а ^ а S ). Дисперсия звуковых волн во второй ( S _i < S < S _ii ) и третьей ( S _ii < S < S _iii ) областях оказывается отрицательной ( с ₀ >  с ^ ), при этом в области II низкочастотная скорость звука конечна, а в III — с ₀ = то . Для последней четвертой области ( S >  S _iii ) характерны положительная акустическая дисперсия с с ₀ (S _iii ) = 0 и тепловая неустойчивость энтропийных мод, возникающая в вязком теплопроводном колебательном-возбужденном газе при достаточно больших значениях степени неравновесности среды S ~ 1,4 , соответствующих мощности нагрева gQ ~ 14 кВт/см ³ . Скорость роста амплитуды тепловой неустойчивости в десятки раз превышает акустический инкремент α.

В линейных моделях с функциями нагрева и охлаждения, зависящими от плотности и температуры, граница устойчивости звуковых волн Si смещается вправо в область больших значений при Ie,T > 0, а низкочастотная скорость звука с0 перестает зависеть от степени неравновесности среды (границы Sii и Siii при этом вырождаются) и является функцией параметров (Qe,T, Ie,T), величина которых определяет три качественно различных закона акустической дисперсии, соответствующих следующим значениям: с0 = 0, 0 < с0 < то, с0 = то. Для этих трех моделей нагрева и охлаждения при опре- деленных значениях степени неравновесности среды (S ~ 1) и частоты (ш ~ ш*) закон акустической дисперсии имеет особенность (разрыв второго рода функции с8(ш) в точке ω*, в которой фазовая скорость звука обращается в ∞). Данная особенность может возникать как в низкочастотной области спектра при шт ^ 1, так и для гармоник с шт ~ 1. В окрестности разрыва значение cs становится аномально высоким, а групповая скорость звука Vg и акустический инкремент а имеют различные знаки слева и справа от разрыва. При ш < ш* получаем Vg < 0 (Vg # cs) и а < 0, а для ш > ш* имеем Vg ff cs и а > 0.

Отметим, что полученные в п. 2 результаты линейного анализа устойчивости акустически активного газа справедливы не только для газовой среды CO ₂ -лазеров, выбранной в качестве примера неравновесного газа, и могут быть использованы при решении как фундаментальных, так и прикладных задач, связанных с распространением звуковых волн в различных колебательно-возбужденных сплошных средах.