Динамика нагрузок на технологическое оборудование лесопогрузчика в поперечно-вертикальной плоскости

Динамические нагрузки на технологическое оборудование в боковом направлении в режиме грузового хода лесопогрузчика возникают при наезде на препятствие одним бортом машины, при смещении центра тяжести груза относительно продольной оси, при движении машины поперек уклона погрузочной площадки. Кроме того, при колебаниях пакета хлыстов вследствие разности жесткости и массы вершинной и комлевой частей деревьев в поперечной плоскости возникает дополнительный момент.

Совпадение указанных факторов во времени обуславливает экстремальные режимы работы, которые необходимо учитывать при проектировании лесопогрузчиков. Для анализа нагрузок на технологическое оборудование в поперечно-вертикальной плоскости необходимо разработать эквивалентные динамические модели системы «лесопогрузчик – груз» при различных сочетаниях подвески корпуса машины и вида транспортируемого груза и их математические модели, учитывающие влияние на уровень нагрузок ряда эксплуатационных факторов: скорости движения, высоты преодолеваемых препятствий, упругих характеристик деревьев, смещения центра тяжести груза от продольной оси машины [1], угла уклона погрузочной площадки.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

В лесной промышленности России на погрузке древесного сырья в виде хлыстов и деревьев с кроной наибольшее распространение получили гусеничные лесопогрузчики на базе лесопромышленных тракторов с полужесткой подвеской корпуса (ТТ-4М, МТ-5). Ведутся работы по созданию и освоению производства лесопогрузчиков на базе тракторов с эластичной подвеской (ТЛТ 100). Исходя из этого, при разработке эквивалентной динамической модели принимались технические характеристики и конструктивная компоновка лесопогрузчика ЛТ-188 на базе трактора ТТ-4М.

При разработке динамической модели учитывается, что наибольшие нагрузки в боковом направлении возникают при расположении стрелы с грузом в вертикальном положении. Масса упругого груза рассматривается сосредоточенной в трех точках, подвешенных на упругих элементах: в центрах тяжести вершинной и комлевой частей расчетного дерева, часть массы дерева, защемленная захватом, приведена к концу стрелы.

На рисунке 1 представлена расчетная схема, составленная для исследования динамики нагрузок, действующих на технологическое оборудование в поперечно-вертикальной плоскости.

В качестве обобщенных координат системы приняты линейные перемещения масс в направлении оси X и угловые перемещения относительно оси Z ( X, β ₂, β ₄, β _с, β _к ). По числу обобщенных координат система имеет четыре степени свободы.

На схеме: m₁ – масса подвижных частей рабочего оборудования, динамически приведенная к концу стрелы; m ‘ , m 2 — массы вершинной и комлевой частей расчетных деревьев, приведенные в их центры тяжести; m₃ – подрессоренная масса трактора и неподвижных частей рабочего оборудования; C 2 , C 2 -изгибная жесткость вершинной и комлевой частей расчетных деревьев, приведенная в их центры масс; K ‘ , K 2 — демпфирующие сопротивления вершинной и комлевой частей расчетных деревьев; l₃, l₄ – расстояния от продольной оси машины соответственно до центров масс вершинной и комлевой частей расчетных деревьев; C_X – изгибная жесткость стрелы в поперечном направлении (в направлении оси X); C ^K – приведенная жесткость корпуса и подвески трактора при кручении; C_P – жесткость упругого элемента подвески корпуса трактора; K_P – демпфирующие сопротивления в подвеске корпуса трактора; L_P – расстояние между вертикальными осями рессор; P_Л , P_П – реакции поверхности пути, передающиеся на рессоры (левую и правую соответственно); M_K – крутящий момент, действующий на корпус трактора; M_C – момент от сил упругости технологического оборудования.

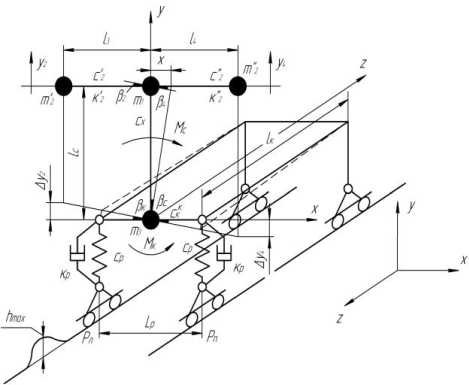
Рис. 1. Эквивалентная динамическая модель лесопогрузчика с полужесткой подвеской корпуса с упругим грузом

Система дифференциальных уравнений движения масс составлена методом кинетостатики (на основе принципа Даламбера). Перемещения центров масс в процессе колебаний происходят относительно положения устойчивого равновесия. При этом силы тяжести уравновешиваются силами упругости при статической деформации упругих звеньев.

Уравнения поперечно-угловых колебаний (перемещений масс в относительном движении) получены в следующем виде:

m2/3 в2 + C 2 (y2 Pkh) /3 + +K '2 (У 2 - Pk/3) /3 = Q2 (t);

mУfa + C2(У4 -Pkl4)/4 ++K2 (y4 - Pkl4 ) /4 = Q4 (t ) ;

(mi + m2)/cPc - Cx (Pc -Pk)/С +

+ C '2 ( У 2 - P k / 3 ) / 3 - C 2 ( У 4 - P k / 4 ) / 4 = Q i ( t ) ;

m3 pZ Pk+Ck Pk - Cx (pc - Pk) 12 +

+ C '2 ( У 2 - P k / 3 ) / 3 - C z2 ( У 4 - P k / 4 ) / 4 = Q 3 ( t ) .

В уравнениях (1) Q 1   (t) , Q 2   (t) , Q 3   (t) ,

Q 4 (t) – обобщенные силы, соответствующие обобщенным координатам системы – внешние возмущающие воздействия на динамическую систему. Внешними возмущающими воздействиями, возбуждающими вынужденные колебания системы в поперечновертикальной плоскости, являются силы инерции масс в переносном движении, возникающие при наезде лесопогрузчика на препятствие одним бортом.

При движении лесопогрузчика через чередующиеся препятствия одним бортом центры масс m₁ , m₂ , m₃ перемещаются в направлении оси Х соответственно на величину L_x(t) и l_x(t) (рис. 2). В качестве источников вынужденных колебаний системы принимаются детерминированные воздействия, возникающие при движении машины через препятствие косинусоидального профиля [2].

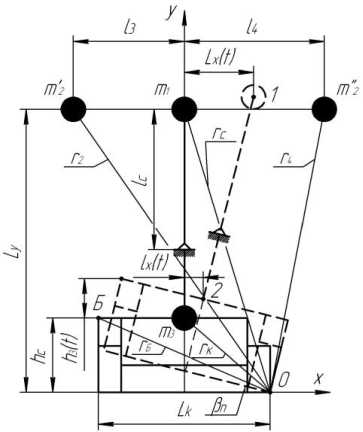
Рис. 2. Схема определения возмущений в поперечновертикальной плоскости

Вынужденные колебания в этом случае являются следствием действия сил инерции масс в переносном движении:

Qi(t )= (mi + m2) d 2 LX (t)/ dt

Q3(t ) = m3 d 2 lx (t)/ dt 2-,

где K Р – коэффициент, учитывающий влияние размеров звеньев кинематики ходовой системы трактора на вертикальные перемещения корпуса при движении машины через препятствие.

Выражение углового ускорения масс в переносном движении:

d 2 L x ( t ) _ r c K p V 2 n ² h m

dt ²

L k L ²

• cos

—; (4)

L

_Р    K p V ²2 п ² h max _co3 2 n Vt .

Lk ‘ L2          L

d ² l x ( t ) _ rK , V^г2 п ² h„

dt ²

r k L ²

2 n Vt

• cos         ,     (5)

где h(t) – текущее значение высоты препятствия; h _max – наибольшая высота препятствия; L – длина препятствия; V – скорость движения машины; t – время движения машины через препятствие.

При использовании в системах дифференциальных уравнений обобщенных координат в виде угловых перемещений ( Р С , Р К , в ) моменты сил инерции масс переносного движения определяется по выражениям:

Mj 1 _ [Ic1 + (m1 + m2 )С ]d^T(6)

dt ²

Mj3 4c 3 +(m 3 • rk P^'.

Здесь I_c 1 , I_c 3 – центральные моменты инерции масс m 1 +m 2 , m 3 относительно осей Z₁, Z₂, проходящих через точки 1,2 (рис. 2)

Ic з_ m3 • pZ ;

Q2 (t) _ Mjl(t) (IB + m2r2 )pP ;

Q4(t) _ M"-2 (t)_(ik + m2r4 )pp , где Ib, Ik - центральные моменты инерции масс m -, m2 ; Г2 , Г4 - радиусы вращения центров масс m -, m2 относительно оси наклона машины.

Из рисунка 2

tg P p = h 3 ( t ) / L_k .                         (11)

При переезде препятствий h _max <  0,5 м p _P < 10 ° .

Для таких значений углов tg P P ~ sin P P ~ P P . P p _ K p h ( t ) / L k ,

Выражения правых частей уравнений (1) принимают следующий вид:

r x т p        \ 2i KpV 2n h       _n 2 n Vt.

^Q 1 ⁽ t ) = ^[ J C 1 ^{+ (} m 1 ⁺ m 2 ) r c ^]--- —2----^{COS      ;}

Q 2 ( t ) _ ( J b + m - r ₂ 2 ) ^{KpV 2}2 П h max COS2V ;

K

Q ₃ ( t ) _ [ J_{c 3} + m₃r_K ²)] K^pV 2 ⁿ h max COS 2V. ; 3           C 3     3 K             2

Q 4 ( t ) _ ( J k + m 2' r 4² ) ^KpV 2 2 П 2 h max COS2V .

Левые части уравнений (1) отображают состояние рассматриваемой системы и включают ее основные динамические характеристики – C_i , K_i , m_i , а также геометрические параметры. Правые части указанных уравнений представляют собой внешние возмущающие воздействия на систему. Они включают в себя эксплуатационные факторы – h _max, V , от которых зависит уровень внешних возмущений на систему и величина динамических нагрузок на элементы системы. Таким образом, разработанные модели позволяют выполнять исследования влияния на величину динамических нагрузок, действующих на рабочее оборудование в поперечно-вертикальной плоскости, конструктивных (параметров системы) и эксплуатационных факторов. Кроме этого, варьированием размеров l₃ , l₄ они позволяют исследовать влияние смещения центра тяжести груза от продольной оси машины на уровень боковых динамических нагрузок.