Динамика неустойчивых решений волнового уравнения с источниками

Введение. Волновые уравнения с линейными и нелинейными источниками (уравнения Клейна–Гордона) относятся к числу фундаментальных уравнений математической физики и позволяют моделировать сложные явления в различных областях естествознания. Задача исследования нелинейных волн - важный элемент динамической теории неравновесных состояний теплофизических, физико-химических и биологических систем [1-3].

Классическое волновое уравнение с источником возьмем в виде

д2т    д2т  _

д12   д(х')2 ~ U ’ где т - функция, характеризующая некоторое физическое свойство среды; t - время; x - декартова координата; w - скорость распространения малых возмущений; х' = x/w; ки = ки (т,t) - функция источника. Например, в терминах теории теплопереноса т - температура, функция ки (т,t) ха рактеризует источники и стоки энергии. Учет пространственно нелокальных эффектов переноса приводит к повышению порядка модельного уравнения (1):

д2 т д2 т      2  д4 т kи .

д t ²    д ( x' ) ²         д ( x' ) ⁴

Здесь х2 — Xi W4, а величина exl есть параметр слабой нелокальности задачи, см. [4] и указанную там библиографию. Для уравнения (2) мы рассматриваем источник ки = кUt + Qg |дт/дx'|; кU, Qg — const,                              (3)

который зависит от модуля градиента искомой функции и в этом смысле является нелокальным. Для размерных и безразмерных уравнений берём одинаковую форму записи, применяя масштабы т b и t b :

( ^т/^т b W ^т , ( tlt b Н t , [ ^х / ( ^wtb ) ]^ ^X ', [ ( k U t ² ) /^т b ]^ k U ’

[ ^e%²/ ( w ⁴ t b ) ]^ ( ex² ) , ( ^k U t b ) ^ ^k U , ( ^Qg t b ) ^ ^Qg .

Изолиния т ( x ', t ) — T i — const перемещается со скоростью N — dx/dt , которая является дозвуко-вой/сверхзвуковой, если M — dx '/ dt — N / w , соответственно, меньше/больше единицы. Предпосылки данной работы состоят в следующем:

• 1.    Для волновых уравнений принципиальное значение имеют кинк-решения, описывающие переход между двумя состояниями равновесия системы «среда–источник». Известные в литературе решения типа «кинк» наиболее подробно изучены для уравнения синус-Гордона [1, 2]. В настоящее время в различных областях физики возникает интерес к волновым уравнениям, содержащим нелинейные реономные источники, которые зависят явным образом не только от искомой функции, но и от времени [5-7]. Такие функции источников позволяют моделировать разнообразные режимы воздействия на скорость и направление движения волны.

• 2.    В динамике нелинейных нестационарных физических процессов важная роль принадлежит задаче построения и описания решений, разрушающихся за конечное время. Обзор работ, относящихся к параболическим уравнениям, представлен в [8, 9]. Условия разрушения и устойчивость решений нелинейных гиперболических уравнений рассмотрены в [10-13]. Еще один аспект этой проблемы - анализ потери гладкости решения за бесконечное время («медленный взрыв») [14].

Цель данной статьи - представить примеры точного аналитического описания неавтомодельных кинков и указать их нетривиальные свойства, проявляющиеся при долговременном взаимодействии среды с источником.

Преобразование независимых переменных. Уравнение (2) запишем в виде системы дифференциальных уравнений:

дv   д20    ,   „       2 ди  дud

---=к к„, О — т+ ех —, — = —, д t д( Х' )2                     дх'   д tд дт        дт             , , .,

• и — —, v — —, d т — udx + vdt .

д x '

Выполним в (4) преобразование независимых переменных ( x ', t ) ^ ( т , t ) :

дvд ди дО    д^О 1  ,

+ и      — кU, дт дт дт2 J

--+ v--и д t    дт л        2 ди

О — т + ех и—, дт ди   ди    дv

--+ v— — и— . д t     дт    дт

Здесь D ( т , t )/ D ( x ’, t ) = д т/d x ' ^ 0 . Изолиния т = т _i имеет скорость

M = dx У dt = - v ( T i , t ) / и ( т , t ) .                                  (8)

Обсудим точные частные решения системы (5)–(7). Для краткости изложения в основной части текста применяется единый термин «кинк», т. е. мы не делаем терминологического различия «кинк»/«антикинк» между профилями, обладающими положительным/отрицательным наклонами дт/d x ' и перемещающимися вправо вдоль оси x ' . Отдельное упоминание антикинка делается там, где он обладает свойствами, отличающимися от свойств кинка.

Классическое волновое уравнение: релаксация кинка. Для уравнений (5)-(7) при в = 0 рассмотрим источник kuи = Qo + вОх, в = exp(rt) , r - const, который явно зависит от времени и при r < 0 релаксирует (t ^ го, в ^ 0) вдоль каждой изолинии т = т : в установившемся по времени состоянии имеем к^ (т, t ^го)^ Qo (т). Вид функций Q0 (т), Q1 (т) будет определен далее в ходе построения решения. Применяя зависимости и = uo (т) + 01^ (т) , V = vo (т) + 0V (т) , находим v0 = -иоMо , Mо - const; V = ±и1;(10)

и о Uo (Mо2 -1) = Qo (т);(11)

+2Uoui (Mо ± 1) = О±(т);(12)

(и1 /и1 ) = (ио /ио) + [r/uо (Mо ± 1)] .

Точка над символом функции означает дифференцирование d / d τ; M 0 – произвольная постоянная, далее для определённости полагаем M 0 > 0; расположение знаков «±» в (12), (13) соответствует формуле (10). Выбор знака «±» влияет на вид реономного источника; суть основного результата вычислений для обоих знаков одинаковая; далее берем в (10) и (12), (13) верхний знак: v 1 = и 1 ,

Q + = Q 1 . Структура соотношений (10)-(13) позволяет задавать априорно функцию и _о ( т ) и получать физически содержательные зависимости О_о ( т ) , Q 1 ( т ) . Рассмотрим частный пример:

ио (т) = Ьо (т2-т2), т > о, т е(-т1,т1); b0, Т1 - const.(14)

Отсюда находим и1 (т) = (С1 /т2 )(т1 + т)1+Л1 (т1 - т)1 Л1, С1 - const,(15)

А1 =(- r )/[ 2Ьот1 (Mо +1)],(16)

Оо (т) = Оот(т2 - т2),(17)

Q1 (т) = QV^ + т)1+Л1 (т1 -т)1-Л1.(18)

Параметры источника Q ₀¹ , Q ₁¹ связаны с константами b 0 , С 1 , М 0 формулами:

о о = 2 b ² ( M о ² - 1 ) , Q 1 =- 4 Ь о C 1 ( M о + 1)/ т ² , Ь о C 1 <  о.

Для Ai в (16), (18) возможны два варианта: Л1 е(-1,-Ло)с(-1,о) и Л1 е(Ло,1)с(о,1), и при этом функции Оо (т), Q1 (т) обращаются в ноль в точках т = 0, т = ±т 1. Величина Ло е(о,1) бу- дет указана в ходе дальнейших вычислений. Выражения (9) и (14), (15) определяют неавтомодельный аналог волны переброса (кинк) между состояниями системы при τ = ±τ1:

и = и о

^Ьо т 2 I ^т 1 ^{- т} J

в

При т = 0 начальный профиль кинка u (x',t = 0) = u0 + и1. x'е (-да,да) имеет наклон и (т = 0,t = 0) = С1 - Ь0т2.                                  (20)

Кинк релаксирует в автомодельное состояние (бегущую волну) вида и = и 0 (т), v = - и 0 M0, т = т(x'-M01), где M0>0 - безразмерная скорость этой волны. В отрелаксировавшем состоянии знак наклона кинка и 0 (т = 0) = -М2                                (21)

остается неизменным именно при Ь₀С <  0. Выполнено неравенство [ и (т = 0, t = 0)/ и 0 (т = 0 ) ] >  1, характеризующее отношение наклонов кинка в начальном и конечном состояниях.

Обсудим свойства источника. В начальный ( t =0) момент времени нелинейный реономный источник ky = Q_o + PQ_y определяется суперпозицией функций (17) и (18); в установившемся по времени автомодельном режиме действует нелинейный источник Q 0 ( т ) . Эта функция имеет экстремумы (максимум и минимум) при т = т _т , где т т = т ^ ,3 ; кроме того, справедливо выражение т = 0, dQ 0/dr = 2 Ь 2 т 2 ( 1 - M ₀ ² ) .

Функция Q 1 ( т ) имеет экстремумы (максимум и минимум) в точках

= 1 (аЛ 'JA—) .

и при этом верна формула т = 0. dQ1 Цт = -4Ь0С,(1 + M0)>0.

Отметим расположение экстремумов, выбор знаков констант b ₀. С 1 и поведение производной TQ 1 ^тт . Если А , е ( - 1, -А ₀ ) , то Ь ₀ < 0. C , >  0.

^{- т} 1 <  42 <(^-т т ) < ⁰ . ⁰ < ^ <  ^т т <  ^т 1 ;

т = -т1. (TQ1 ^тт)^да; т = т1. dQ1 Цт = 0.

Если А 1 е ( А ₀,1 ) , то Ь ₀ >  0. С 1 <  0.

• ^{- т} 1 <(^-т т ) < ^т т ²⁾<  ⁰ . ⁰ <  ^т т < ^ <  ^т 1 ; т = - т 1 . TQ 1 Цт = 0; т = т 1 . ( TQ 1 Цт ) ^да .

В качестве входных параметров задачи возьмем: 1) размер интервала (-т1,т1), в котором существует волна переброса; 2) наклоны кинка в начальном (20) и отрелаксировавшем (21) состояниях - знаки этих наклонов должны быть одинаковые; 3) отношение наклонов функции источника dQ^)  = a0 = Ь (M0 - 1)т2/(2C1).

• V ^dQ 1 / ^{Т т} )_{т = 0}

Тогда параметры решения подсчитываются по формулам:

Ь 0 = - и 0 ( т = 0 )/ т 1 . С = и 1 ( т = 0 ) . M 0 - 1 = 2 а 0 С^ ( Ь_о т 1 ) .

Следовательно, скорость бегущей волны сверхзвуковая при а ₀<0; в этом случае между функциями Q 0 ( т ) и Q 1 ( т ) имеется конкурентное взаимодействие, которое завершается формированием сверхзвуковой волны переброса, M ₀>1. Если 0 <  а ₀ < [ и ₀ ( т = 0)/2 и 1 ( т = 0 ) ] , то конкуренция отсутствует ( Q ₀ Q 1 >  0 ) , и процесс завершается формированием дозвуковой бегущей волны, M ₀ е ( 0,1 ) . В ходе дальнейшего анализа будут указаны оценки начальной скорости точки перегиба кинка, при которых автомодельная волна является дозвуковой либо сверхзвуковой. Перечисленные качественные свойства источника при А 1 е ( А ₀,1 ) показаны на рис. 1. Иллюстрация варианта А 1 е ( - 1, А ₀ ) по своему физическому содержанию аналогичная и здесь не приводится.

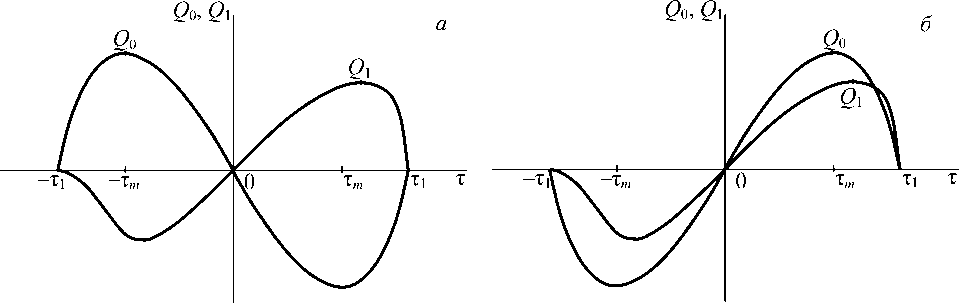
Рис. 1. Функции источника k _и = Q ₀ + в Q 1 : а - сверхзвуковой вариант M ₀ > 1; б - дозвуковой вариант 0 <  M ₀< 1

В точке перегиба релаксирующего кинка x' = x'у ( t ) условие д^т, д ( x ') 2 = 0

дает уравнение

ди/дт = 0, определяющее функцию т = т f ( t ) :

Tf =

^А 1 ^т 1 A f

^{1 +} A f

Af =

- С в ^Ь 0 ^т 12

f т1 + тf

A Ai

l т1 - т J

dтf   r4 (А1т1 - Ч )(т12 - т2)

dt   Ат (тf — 2тf Ат + т )

Рассмотрим скорость dx*/ jdt = M f точки перегиба:

M f + 1 =

dт f    ,         х /   \   —1

+ ( ^M 0 ⁺ 1 ) и 0 т ) И f ,

u f

= и 0 (тf) + PU1 (тf ) .

Если А1 е(—1, —А0), то тf < 0, dтf/dt > 0, и0 (ту )> 0, Uу > 0, А1т1 < тf < 0 ; напомним, что здесь b0 < 0, C1 > 0. Если А1 е(А0,1), то ту > 0, dтf/dt < 0, и 0 (ту )< 0, uf < 0; 0 < тf <А1т1, b0 > 0, C1 < 0. Таким образом, для всех допустимых значений A1 имеем

0 <( и 0/и )^. < 1, и -1 (dтf/dt )> 0, А1тf > 0, ^тf /(Ат — тf )J> 0 .

В установившемся по времени состоянии получаем:

t —— ^ , A f —— 0, т у —^ 0, ( d т f d dt ) — — 0, M f —— M 0 .

Формулу (23) запишем в виде

M f +1    7 XX

——-=R2 (п); п=ту/(А1т1), 0 < п <1, м 0 +1

R2 (п) = (1 — п)[( VА2 ) — п2 ]/[п2 — 2п + (VА2 )] .

Пусть в начальном состоянии точка перегиба имеет некоторую скорость M f = M f >  0, и при этом п = п 1 = т f ( t = 0 )/( А 1 т 1 ) , где т 2 ( t = 0 ) <  т 2 . Обозначим R 2 = R ² ( п = п 1 ) и укажем условия, при которых решение имеет физический смысл. Расчеты показывают, что А ₀ = 1/ V2, а значения параметров n 1 , A 1 должны удовлетворять неравенствам

0<щ <(1 -^(1/A2)-1), (12)<а2 < 1, которые приводят к оценке R2 > 1. Дозвуковая волна М0 е (0,1) существует, если

R 1 ² < ( 1 + M f ) < 2 R 2 .                                  (25)

Сверхзвуковая волна M0 > 1 существует, если 1 + Mf > 2R12 . Следовательно, исходное допуще ние M0 > 0 будет выполнено, если начальная скорость Mf точки перегиба превосходит пороговое значение (R12 -1) > 0 . Еще одно пороговое значение, а именно: Mf = 2R12 -1 разделяет дозвуковой и сверхзвуковой режимы движения автомодельного кинка. Отметим, что в формуле (24), дающей зависимость Mj = Mj (7), аргумент 7е(0,71 ] изменяется от начального значения п1 в сторону меньших значений, п ^ (+0).

Возвратное движение точки перегиба. До сих пор мы рассматривали устойчивый ( r < 0) режим релаксации кинка. Обсудим теперь неустойчивый процесс, происходящий при r >  0. Все формулы решения остаются без изменения, но, согласно (16), требуется поменять знаки констант b ₀ и C 1 ; знак произведения этих констант по-прежнему отрицательный. При А 1 е ( А ₀,1 ) нужно взять b₀ <  0, C 1 >  0 ; при А 1 е ( - 1, -А ₀ ) нужно взять b ₀ >  0 , C 1 <  0. Из этого следует, что при r >0 и r < 0 различаются знаки наклона кинка: см. (20), (21). Вид функций источников (17), (18) и процедура задания начального состояния системы «среда - источник» полностью сохраняются. При r > 0 имеем неустойчивое решение (9), (19); вдоль каждой ненулевой изолинии т = т i источник с течением времени ( t ^ го, в ^ ю) становится неограниченно большим. Проанализируем поведение точки перегиба кинка. Пусть в начальном состоянии (в = 1) имеем п = п 1 , M f- = M f >  0. Отличие от устойчивого режима r < 0 в том, что теперь аргумент 7 е [ 7 1 ,1 ) увеличивается от своего начального значения и стремится к 1 слева, см. (22), (24). Формально это означает, что результатом пространственно-временной эволюции кинка является сильный разрыв функции т ( x ', t ) в точке x ' = 0. На разрыве функция изменяется скачком от (-т 1 ) до т 1 . В физическом отношении целесообразно рассматривать неустойчивый процесс на конечном интервале времени, предшествующем остановке точки перегиба. Запишем (24) в виде

M f = ( M ₀ + 1 ) R ² - 1.

Здесь M f = M f ( 7 = 7 1 ) > 0, M j ( 7 ^ 1 ) ^ ( - 1 ) < 0. Таким образом, для непрерывной функции M f ( 7 ) существует конечный момент времени t = t * < го , 7 * = ^ т j ( t * )/( А 1 т 1 ) ] <  1, когда скорость точки перегиба равна нулю: M f- ( 7 = 7 * ) = ( M ₀ + 1 ) R ² ( 7 = 7 * ) - 1 = 0. При t >  t * происходит возвратное движение точки перегиба, являющееся предвестником сильного разрыва.

Нелокальное решение. Для нелокального уравнения (2), преобразованного к системе (5)(7), кинковое решение строим в виде

• — = Г в , u = t U ( — ) , v = t V ( — ) , в = exp ( rt ) .                        (25)

В этом случае функция источника (3) представляется формулой k _и = t Q ( — ) , где Q ( — ) подсчитывается посредством U ( — ) . На основе (25) получаем

0 = t ( 1 + ex ² 5 ) , 5 = U ( U + — U ) ,

5 0/ S t = 1 + ex ² ( 5 + — 5 ) ,

• V ( v + — V ) - r — V - U ( U + — U ) | ⁰ - ex 2 U ² — d- ( 5 + — 5 ) = Q ( — ) ,           (26)

Г                 —

V = r - M 0 U , M 0 = const. (27) Здесь точка над символом функции означает дифференцирование d / d ξ. М 0 – произвольная постоянная, являющаяся параметром начального состояния кинка. Нетрудно видеть, что М ₀ есть безразмерная скорость линии ξ = const. Далее берем для определенности M 0 > 0. При r = 0 получаем бегущую волну т = т ( x ' - M 0 t ) . Уравнениям (26), (27) удовлетворяют следующие функции:

U ² = ( A 2 Д² ) - A 2 , 5 = - A 0 = const,

Q ( ^ ) = k U - 2 rM o U , к U = r ² - A 02 ( M 22 - 1 + ex 2 L ) . (28) Отсюда находим

U = ±(A2в - V.:2 )V2,\A, (29) где А0, А1 – положительные постоянные. В данном решении мы рассматриваем вариант т C ( ^w,тw), тw =( All A0 ) exp (rt) , Al > A0Tw (t = 0)> 0 . (30) Для случая (9 ^9x')> 0 берем в верхней части (т > 0) кинка знак «+» в (29), т. е. U > 0; в нижней части (τ < 0) берем знак «–», т. е. U < 0. Тогда для кинка имеем u = дт/ 9x' = (Al в - A2T2 )12, Qg = -2 rM0. (31) Аналогичным образом нужно действовать при (9 А9x') < 0. Параметры источника к11, Qg связаны с параметрами решения А0, А1, r, M0 формулами (28), (31). Точка перегиба кинка τ = 0 движется со скоростью M0. Таким образом, имеем аналог волны переброса в интервале с нестационарными границами: (дт/9x')^ 0 при т ^±тw(t).

Рассмотрим верхнюю часть кинка, т е [ 0, т _w ) . Скорость перемещения изолинии т = т i > 0 равна

M i ( t ) = M 0 - ( т /A/ )( A i ² в - A ^ ) ^{- 1} 2 . (32)

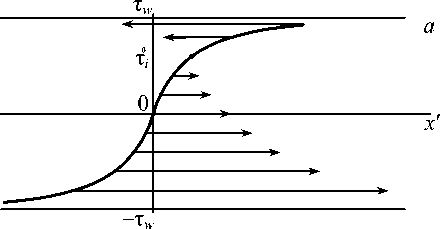
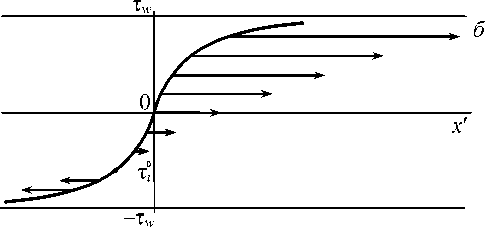
Рис. 2. Распределение скоростей изолиний в фиксированный момент времени t = t 1 ≥ 0: а – неустойчивый вариант; б – устойчивый вариант.

Черным кружком отмечена неподвижная изолиния, стрелка указывает направление движения

Возьмем любой конечный момент времени t = 11, 0 < 11 < да, обозначим т, = 8iтw(t1) и получим Mi (ti ) = M0-(r 8 J A )(1 - 82 )-12, где 8i e( 0,1) - номер изолинии. Пороговое значение

8 0 = M 0 A 0 ( r ² + M 0 ² A 2 ) ^{- 1} 2                                (33)

относится к неподвижной изолинии. Отрицательные скорости имеют изолинии, находящиеся в конечной окрестности верхней границы т = т _w ( t ) >  0, т. е. здесь 8 , е ( 8⁰,1 ) . Изолинии т i > 0, обладающие положительными скоростями, располагаются непрерывным образом на двух участках:

1) в конечной окрестности точки перегиба т = 0, движущейся с положительной скоростью M 0 >

0, а именно: 5i е(о,50); 2) во всей нижней части кинка, т ^(-тw,0], т, =- 5t Tw (ti )< 0, 5, е( 0,1), Mi (ti ) = M0 +(r 5, /A )(1 - 52 )—1

Вогнутый участок движется с положительной скоростью навстречу той части выпуклого участка, что примыкает к границе t = Tw, рис. 2, а. Такое состояние - неустойчивое, и оно влечет за собой монотонное неограниченное расширение при t>t1 границ интервала (-Tw, Tw). Из (32) и (33) следует, что в момент времени t = t* > t1 обращается в ноль скорость изолинии 5irw (t1): в* = в5zК0, 5z е(б0,1), в = exp (rt1), в* = exp (rt*). Чем ближе тi (со стороны больших значе ний) к ri0 = 50 Tw (t1), тем быстрее скорость Mi (t) принимает нулевое значение; при t > t* скорость этой изолинии становится положительной. Таким образом, при t > tx наблюдается непрерывный процесс перемены знака («минус» ^ «плюс») скорости изолиний. Вместе с тем существенно, что при t > t1 в области определения решения появляются новые изолинии, примыкающие изнутри к левой/правой границам интервала (-Tw, Tw) и имеющие, соответственно, положитель-ные/отрицательные скорости. В данном случае нет разрушения кинка из-за того, что интервал (-Tw, Tw) монотонно расширяется с течением времени: в каждый конечный фиксированный момент t е[0,t2), 0 < t1 < t2 <ж решение непрерывно, и наклон кинка, согласно (31), имеет максимум при т = 0. При t^да область определения решения стремится занять 1-й и 3-й квадранты на плоскости (x‘, т), и тогда x' = 0 - сильный разрыв. Следует обратить внимание на важное свойство нестационарного решения (25), (31): v = дт/дt = 0 при т = тj (t), где 0 < тj < rw,

^jhw ) = ⁵⁰ .

Функция t = t ( x ', t ), в отличие от автомодельного кинка, немонотонная по отношению к аргументу t : при каждом фиксированном конечном x' она имеет максимум. Условие v (т j , t ) = 0 выполнено в верхней части кинка, причем ( д 2 т д t ² ) <  0. Индекс j относится к функциям на линии (34): ^ j = т j / в = м 0 A 1/ ( Г ² + м 2 A 0 ) 12 .

При r < 0 получаем устойчивый режим вырождения кинка в однородное состояние т = 0. Неподвижная изолиния т , = т⁰ = -д⁰т._х ( t ) находится в нижней части кинка: - т _w <  т j <  т⁰ <  0. При т = т j ( t ) имеем v (т j , t ) = 0, ( д ² т /5 t ² ) >  0, т. е. для каждого фиксированного конечного x ' функция т=т ( x ‘ , t ) имеет минимум по отношению к аргументу t . Границы интервала (-т _w , т _w ) сближаются, потому что теперь выпуклый участок движется с положительной скоростью навстречу той части вогнутого участка, которая примыкает к нижней границе т = - T w , рис. 2, б . Кинк в ходе своей эволюции стремится распрямиться в линию т = 0: в ось x ‘ .

Остается указать роль источника в возникновении неустойчивости и дать последовательность расчета констант, содержащихся в построенном решении. Исходными являются параметры kU, Qg, а также величины тw (t = 0), A1 = и (т = 0, t = 0), определяющие начальное состояние кинка. Неавтомодельность решения (25), (27), (31) обусловлена именно воздействием градиентного источника Qg |u|, аддитивно входящего в (3): если Qg = 0, то r = 0, т. е. в = 1. Согласно (31), для кинка (дт/дx') > 0 знак r противоположен знаку Qg: имеем устойчивость/неустойчивость при положительном/отрицательном Qg. Для антикинка (дт/дx')< 0 наблюдается инверсия знаков: в этом случае Qg = 2 rM0, поэтому имеем устойчивость/неустойчивость при отрицатель-ном/положительном Qg . Итак, неустойчивому кинку/антикинку соответствует градиентный сток (Qg < 0)/источник (Qg > 0). Устойчивость автомодельных кинк-решений нелокального волнового уравнения (2) с полиноминальной по т нелинейностью источника рассмотрена в [15].

Порядок расчетов: из (30) получаем A0 = A1 ,tw (0). Далее применяем формулу Qg = 4r2M0 и исключаем M02 в выражении для k1υ , см. (28). Это дает биквадратное уравнение для r2, которое всегда имеет один положительный корень: вычисляем r и присваиваем ему знак, соответствующий знаку Qg, а затем определяем скорость точки перегиба M0 = ^QgД-2r)J > 0 . Роль параметра нелокальности среды £%

видна из следующих неравенств:

d( r2 }/d£s%2 )> 0,

d( M02 ^д(^£^22 )< 0.

Заключение. Получены точные частные решения типа «кинк» для волновых уравнений (1) и (2). Выполнен анализ неустойчивых состояний системы «среда – источник». Неустойчивый вариант решения (9) даёт сильный разрыв при t → ∞, а предвестником начала разрушения кинка служит возвратное движение его точки перегиба. Функция (31) представляет решение нелокального уравнения (2) с источником (3). Основной результат: инверсия знака параметра Q g приводит к инверсии условий устойчивости кинка и антикинка.