Динамика перепутывания двух дипольно-связанных сверхпроводящих джозефсоновских кубитов, взаимодействующих с двумя резонаторами

Перепутанные состояния в настоящее время являются фундаментом квантовой криптографии, квантовых коммуникаций и квантовых вычислений [1–3]. Соответственно одной из основных задач современной квантовой информатики является разработка эффективных схем генерации и механизмов стабилизации и контроля степени перепутывания кубитов, взаимодействующих с различными видами полей и другими типами окружений. В настоящее время предложены и экспериментально реализованы многокубитные перепутанные состояния атомов и ионов в резонаторах, оптических и магнитных ловушках, а также различных искусственных атомных объектов, таких как квантовые точки, примеси в твердых телах, сверхпроводящие цепи с джозефсоновскими переходами и др. [4–6]. В последнее время в качестве наиболее перспективных физических систем для реализации квантовых приборов, использующих перепутанные состояния, таких как квантовые компьютеры, квантовые сети и другие рассматриваются сверхпроводящие джозефсоновские кубиты [7]. Важной особенностью таких кубитов является то, что их эффективные дипольные моменты значительно превосходят по величине дипольные моменты естественных атомов, а сами кубиты представляют собой макроскопические объекты размерами в несколько микрон.

Сверхпроводящие кубиты представляет собой LC сверхпроводящие цепи, разорванные одним или несколькими джозефсоновскими переходами. Для целей квантовых вычислений обычно используют кубиты с тремя или четырьмя джо-зефсоновскими переходами. В отличие от цепей с одним переходом, в случае нескольких джозеф-соновских контактов бистабильное состояние кубита возникает при сколь угодно малой индуктивности цепи, что позволяет уменьшить влияние на кубит внешних электромагнитных шумов. При введении в схему нелинейности с помощью джозефсоновских переходов, эквидистантные уровни LC сверхпроводящего осциллятора перестают быть таковыми, и два самых низких уровня могут использоваться для того, чтобы закодировать кубит. Квантовая информация в кубите кодируется направлением и силой тока для двух бистабильных состояний. Такие кубиты могут управляться микроволновым излучением, напряжением, магнитным полем и токами, их состояния могут быть измерены с высокой точностью c использованием специальных чипов [7]. Большое количество сверхпроводящих кубитов может быть соединено в цепочки, поэтому такие сверхпроводящие кубиты рассматриваются в качестве одной из возможных реализаций логических элементов квантового компьютера или квантовой сети. Времена когерентности сверхпроводящих кубитов могут достигать десятков © Башкиров Е.К., 2016

микросекунд. Связь между соседними кубитами может быть реализована за счет индуктивного взаимодействия (так называемого эффективного диполь-дипольного взаимодействия). Интенсивность взаимодействия кубитов может контролироваться с помощью электроники. Удаленные сверхпроводящие цепи (кубиты) могут быть соединены через «полости» – микроволновые копланарные резонаторы или электронные LC сверхпроводящие контуры (в первом случае кубиты взаимодействуют друг с другом путем обмена реальными или виртуальными фотонами, во втором – квантами колебаний электронной плотности). В последние годы со сверхпроводящими цепями удалось выполнить простые алгоритмы квантовых вычислений, создавать много-кубитные перепутанные состояния, состояния с определенным числом «фотонов» в «резонаторе» и осуществить другие манипуляции, необходимые для квантовых вычислений и квантовых сетей [4–7].

Взаимодействие кубитов с окружением приводит к декогерентности, так что исследуемая система эволюционирует в состояние, непригодное для целей квантовой информатики. Однако, даже при отсутствии взаимодействия кубитов с окружением, степень перепутывания кубитов может меняться с течением времени, при этом возможны эффекты мгновенной смерти и рождения, перепутывания на временах меньших времени декогеренции [8]. В частности для кубитов, взаимодействующих с квантовыми полями в идеальных резонаторах, изменение степени перепутывания кубитов вызвано осцилляциями Раби. Поэтому важной проблемой современной квантовой информатики является разработка эффективных механизмов, обеспечивающих стабилизацию перепутывания сверхпроводящих кубитов, взаимодействующих с квантовыми полями. В последнее время большое внимание уделяется также изучению поведения сверхпроводящих кубитов в гибридных схемах квантовой информатики. Одним из наиболее интересных примеров таких гибридных систем являются сверхпроводящие кубиты, взаимодействующие с одной или несколькими двухуровневыми системами. Кубиты всегда связаны с неконтролируемыми степенями свободы, которые приводят к декогеренции в их динамике. Такая декоге-ренция не всегда связана со внешними степенями свободы. В ряде недавних экспериментов были обнаружены осцилляции Раби кубитов с большим временем декогеренции за счет взаимодействия с некоторыми внутренними квантовыми степенями свободы, которые зачастую можно моделировать как взаимодействие кубита с микроскопической квантовой искусственной двухуровневой системой [9]. Большие времена декогеренции позволяют надеяться на создание гибридных многокубитных систем для квантовых вычислений [10]. Двухуровневые системы в этом случае представляют собой искусственный атом или группу атомов, возникающие за счет туннелирования между двумя поверхностными конфигурациями и связанные с наличием дефектов внутри туннельного джозефсоновского перехода. Когда частоты перехода в двухуровневом атоме и кубите близки, между ними возникает сильная связь, приводящая к дополнительной декогеренции состояния кубита. В работе [11] показано, что такие дефекты могут рассматриваться также как «поддельные резонаторы». Авторы наблюдали значительное число таких «поддельных резонаторов» с различными резонансными частотами вплоть до 60 МГц и исследовали осцилляции Раби за счет взаимодействия зарядового кубита с такими «поддельными резонаторами». Затухающие осцилляции Раби указанного типа наблюдались для зарядовых, фазовых, потоковых кубитов и транзмонов в большом количестве работ (см. ссылки в [12]). В работе [13] были впервые экспериментально получены осцилляции параметра перепутывания (согласованности) для двухчастичной системы, состоящей из макроскопического джо-зефсоновского сверхпроводящего кубита и связанной с ним двухуровневой микроскопической двухуровневой системы («поддельного резонатора»). При этом исследовалось поведение системы, как при приложении внешнего периодического поля, так и спонтанная динамика системы. В эксперименте использовался джозефсонов-ский фазовый кубит с изменяемым потоком. Кубит представлял собой кольцо с индуктивностью 770 пГн, содержащее джозефсоновский переход. Энергетическое расстояние между базисными состояниями кубита можно было настраивать, меняя магнитный поток, индуктивно связанный с кольцом. можно было рассматривать как двухуровневую систему. Взаимодействие кубита с дефектами атомного размера в туннельном барьере джозефсоновского перехода приводит к наличию особого канала декогерентности. Из анализа особенностей осцилляций Раби для насе- ленности возбужденного уровня кубита были определена константа взаимодействия кубита и двухуровневой системы: д / п — 76 МГц и частота Раби кубита под действием микроволнового поля Q / 2п = 63 МГц. Таким образом, динамика сверхпроводящих кубитов, взаимодействующих с искусственными двухуровневыми системами аналогична их динамике за счет обмена «фотонами» с резонатором.

В настоящее время имеется большое число работ, в которых как теоретически, так и экспериментально исследована динамика перепутывания систем кубитов, взаимодействующих с квантовыми полями резонаторов [5; 6]. Однако основное внимание уделялось рассмотрению взаимодействия кубитов с общим полем единственного резонатора. Представляет интерес изучить динамику перепутывания кубитов, взаимодействующих с индивидуальными резонаторами, при этом взаимодействие кубитов может быть реализовано за счет их эффективного диполь дипольного взаимодействия.

1. Модель и ее точное решение

Перейдем к описанию рассматриваемой модели. Рассмотрим два идентичных сверхпроводящих кубита, каждый из которых взаимодействует с изолированной модой микроволнового поля своего копланарного, электронного или «поддельного» резонатора. Для простоты в настоящей работе остановимся на рассмотрение резонансного взаимодействия между кубитами и резонаторами, а также пренебрежем эффектами диссипации, т. е. будем изучать динамику систе- мы на временах меньших времени декогерентности. Будем полагать, что взаимодействие между кубитами осуществляется за счет эффективного диполь-дипольного взаимодействия. Гамильто- ниан рассматриваемой модели в представлении взаимодействия можно записать в виде:

H = й g A (a ⁺° 1 + a ст + ) +

+ й д в ( b ⁺^ 2 + b ^ 2 ) + й J ( ст + ст - + СТ + СТ - ),

где a+ (a) — оператор рождения (уничтожения) моды поля резонатора A; b+ (b) — оператор рождения (уничтожения) моды поля резонатора B; ст+ (ст-) — повышающий (понижающий) оператор для первого кубита, взаимодействующего с резонатором A; ст+ (ст-) — повышающий (понижающий) оператор для второго кубита, взаимодействующего с резонатором B; gA и gB – константы взаимодействия кубитов с резонаторами A и B соответственно и J – константа эффективного диполь-дипольного взаимодействия между кубитами. В дальнейшем для простоты будем полагать, что gA — дв — д.

Положим, что в начальный момент времени кубиты приготовлены в белловском перепутанном состоянии вида cos 9 | + 1 , - - ) + sin 9 | — 1 , + 2 ) , а поля резонаторов находятся в вакуумном состоянии (температура, при которой функционируют цепочки сверхпроводящих колец, составляют микрокельвины, поэтому влиянием тепловых «фотонов» на динамику кубитов можно пренебречь). В результате начальное чистое состояние системы описывается волновой функцией вида

| V ⁽⁰⁾ ) = ^{(cos 9} | ⁺ 1 , ^— 2 ) ^{+ sin 9} | ^- 1 , ⁺ 2 ) ) | ⁰ A , 0 B X ⁽²⁾ где | + i ) — возбужденное и | - i ) — основное состояние i -го кубита соответственно. Такое состояние может быть реализовано, например, за счет взаимодействия кубитов с общим полем третьего копланарного или электронного резонатора [14]

Для системы с гамильтонианом (1) и начального состояния (2) временная волновая функция может быть представлена в виде

| V ⁽ t ) ) = ^C 1 ⁽ t ) | ^- i , ^- 2 ^; 0 a ,1 в ) ⁺

^{+ C} 2 ⁽ t ) | ^- 1 , ^- 2 ^{; 1} A , ⁰ B ) ^{+ C} 3 ⁽ t ) | ^- 1 , ⁺ 2 ^{; 0} A , ⁰ B ) ⁺

+ C4(t) | +1, -2;0A, 0B), где

C 1 ( t ) = exp( - i a t / 2) cos 9 x

x

, l~2 7   /      i cos(V a ² + 4 gt /2)

cos(V a ² + 4 gt /2)--, ^y

V a ² + 4

C 1 ( t ) = exp( - i a t / 2) sin 9 x

x

cos

+ 4 gt /2) + i c ^Os(V ^{a + 4} gt ^/2)

+ 4

С з ( t ) =

_ 2i exp(-iat / 2) sin 9 sin(Va2 + 4 gt / 2) —--.      =------------------ a2 + 4

С з ( t ) —

2 i exp( - i a t / 2) cos 9 sin( V a ² + 4 gt / 2)

V a ² + 4

Имея точное решение для волновой функции модели, мы можем перейти к вычислению степени перепутывания кубитов.

2.    Вычисление параметра перепутывания двух кубитов

Для определения меры перепутывания кубитов воспользуемся параметром Переса-Хоро-децких или «отрицательностью»:

б ( t ) =- 2 ^ ц - ,                                    (3)

i где ц- — отрицательные собственные значения частично транспонированной по переменным одного кубита атомной матрицы плотности T рqUbits. Для неперепутанных состояний полагают, что б = 0. Для перепутанных состояний: 0 < б < 1. Максимальной степени перепутывания соответствует значение б = 1.

Редуцированную матрицу плотности кубитов можно найти, усредняя полную матрицу плотности всей системы по полевым переменным

Р qubits ( t ) = T F | V ( t )X v ( t ) | .

В результате в двухатомном базисе | — 1 , — 2 ) , | - 1 , + 2 ) , | + 1 , - 2 ) , | + 1 , + 2 ) Для рассматриваемой

модели имеем
	Г и	0	0   0 Л
	0	V	H 0
р qubits ( t )	0	H *	W 0	,	(4)
	ч 0	0	0   0 у
где
U ( t ) = | С 1 ( t ) |2		+ | С 2 ( t ) | 2 ,		V ( t ) = | С з ( t ) |2,
W ( t ) = | С 4( t ) |2		,     H ( t ) = С з ( t ) С * ( t ).

Частично	транспонируя матрицу (4) по пере-
менным одного кубита, получаем
	*
	и 0  0 H
	0 V 0   0
T 1 р qubits ( t )	0  0 W 0	,                           (5)
	ч H 0   0    0 у

Матрица (5) имеет всего одно отрицательное собственное значение вида

Ц - = 1 / 2[| U |² - 7| U |² + 4 | H |² ].

Тогда параметр Переса-Хородецких будет иметь вид:

б = 7| U |² + 4 | H |² - | U |² .                            (6)

Для численного моделирования временной зависимости параметра перепутывания кубитов (6) необходимо выбрать значения параметров модели, достижимые в современных экспериментах по квантовой электродинамике сверхпроводящих кубитов.

3.    Обсуждение результатов

В многочисленных экспериментах со сверхпроводящими кубитами, взаимодействующими с копланарными или электронными резонаторами, а также «поддельными резонаторами» в виде дефектов в области туннельных переходов кубитов, достигались значения константы ди-поль-фотонного взаимодействия g в интервале от десятков МГЦ до десятков ГГЦ [5–6; 9–13]. С другой стороны, в двухкубитных схемах в последнее время удалось реализовать эффективное диполь-дипольное взаимодействие кубитов с интенсивностью J в несколько ГГц [5; 6]. Это означает, что в реальных экспериментах относительная эффективная константа диполь-диполь-ного взаимодействия а = J / g может достигать нескольких десятков единиц.

Результаты численного моделирования параметра перепутывания для различных начальных состояний двухатомной системы вида (2) и различных значений относительной интенсивности диполь-дипольного взаимодействия кубитов представлены на рис. 1 и 2. Из рисунков хорошо видно, что для рассмотренного перепутанного начального состояния кубитов наличие интенсивного диполь-дипольного взаимодействия приводит к существенной стабилизации степени перепутывания кубитов.

Заключение

Таким образом, наличие индуктивного взаимодействия между двумя кубитами (которое в терминах квазиспиновых операторов может быть описано аналогично диполь-дипольному взаимодействия естественных атомов), каждый из которых взаимодействует со своим копла-нарным, электронным ( LC сверхпроводящим контуром) или «поддельным» резонатором, соответствующим дефекту в области туннельного перехода, может быть использовано в качестве эффективного механизма стабилизации первоначально наведенного перепутывания сверхпроводящих кубитов, что позволяет существенно увеличить время выполнения необходимых логических операций с перепутанными состояниями таких кубитов. В настоящей работе мы не принимали в расчет диссипативные процессы. Особенно существенны такие процессы при описании динамики кубитов, взаимодействующих с «поддельными резонаторами». Кроме того мы ограничились рассмотрением случая идентич-

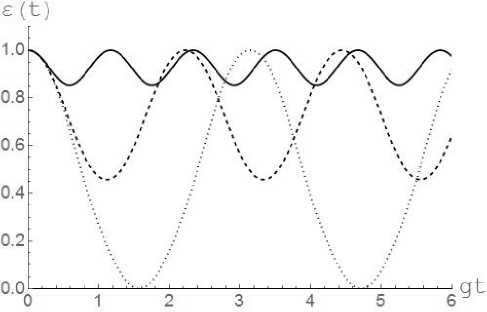
Рис. 1. Временная зависимость параметра перепутывания s ( t ) для начального состояния вида (2) и значений параметра перепутывания 0 = п /4 и эффективной константы ди-поль-дипольного взаимодействия: J = 0 (точечная линия), J = 2 g (штриховая линия) J = 5 g (штриховая линия)

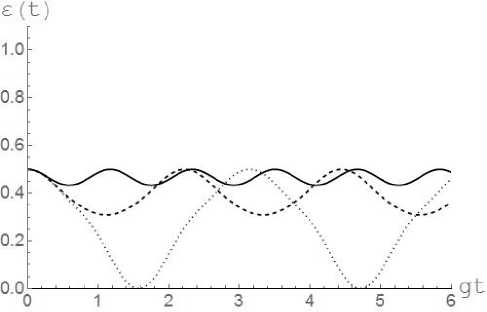
Рис. 2. Временная зависимость параметра перепутывания s ( t ) для начального состояния вида (2) и значений параметра перепутывания 0 = п /6 и эффективной константы ди-поль-дипольного взаимодействия: J = 0 (точечная линия), J = 2 g (штриховая линия) J = 5 g (штриховая линия)

ных кубитов и резонансного взаимодействия между кубитами и полями резонаторов. Рассмотрение более реалистичной модели, учитывающей различные виды диссипации энергии в системе и расстройку, на основе микроскопических кинетических уравнений в марковском и немарковском приближениях, и оценка на их основе времен декогеренции, будет являться предметом нашей следующей работы.

Работа выполнена в рамках госзадания Министерства образования и науки Российской Федерации № 1394.