Динамика перепутывания кубитов в трехкубитной модели Джейнса - Каммингса для бисепарабельных начальных состояний
Автор: Багров А.Р., Башкиров Е.К.
Журнал: Физика волновых процессов и радиотехнические системы @journal-pwp
Статья в выпуске: 4 т.27, 2024 года.
Бесплатный доступ
Обоснование. Для работы квантового компьютера должен быть реализован набор универсальных вентилей, например двухкубитный вентиль типа контролируемое отрицание плюс однокубитные вращения. В качестве универсальной альтернативы возможно использование трехкубитных вентилей. В этой связи представляется весьма актуальной задача исследования динамики систем трех кубитов в микроволновых резонаторах, в частности изучение наиболее эффективных схем генерации, управления и контроля перепутанных состояний кубитов.
Кубиты, резонатор, квантовое тепловое поле, бисепарабельные состояния, перепутывание, отрицательность, мгновенная смерть перепутывания
Короткий адрес: https://sciup.org/140309030
IDR: 140309030 | УДК: 537.86:530.145
Текст научной статьи Динамика перепутывания кубитов в трехкубитной модели Джейнса - Каммингса для бисепарабельных начальных состояний
Многокубитные перепутанные состояния – ключевой ресурс для многих квантовых информационных задач [1–4]. В настоящее время известны различные типы и классы перепутанных состояний [5–7]. К наиболее известным перепутанным состояниям относятся белловские перепутанные состояния, бисепарабельные перепутанные состояния, истинно перепутанные состояния Грин-бергера – Хорна – Цайлингера (GHZ-состояния), истинно перепутанные состояния Вернера (W-состояния) и др. Для каждого из указанных состояний предложены многочисленные способы применения в области физики квантовых вычислений, в частности для коррекции ошибок, квантовых коммуникаций, квантовой криптографии, квантовой метрологии и др. [8–11]. В последнее время появилось множество экспериментальных работ, в которых показана возможность генерации мно-гокубитных перепутанных состояний для кубитов различной физической природы [1–4]. В настоящее время предложен ряд количественных критериев перепутывания двухкубитных систем: отрицательность и ее расширения, согласованность, G-согласованность, геометрическая мера перепутывания и др. [5–7; 12–16]. Однако для много-кубитных квантовых систем ситуация становится более сложной, поскольку для таких систем существует несколько различных классов перепутанных состояний [17–19]. Трудности теоретического описания перепутанных состояний существенно возрастают с увеличением числа кубитов в системе. Поэтому в настоящее время особый интерес вызывает изучение динамики перепутывания трехкубитных систем. Для трехкубитных систем существуют три типа чистых перепутанных состояний: сепарабельные или полностью разделимые, бисепарабельные и истинно перепутанные состояния. Мы имеем дело с сепарабельным состоянием, если трехкубитный вектор состояния
Е^Н © Багров А.Р., Башкиров Е.К., 2024
системы является тензорным произведением трех однокубитных векторов состояния. Если трехку-битное состояние сепарабельное по отношению к двум подсистемам, одна из которых состоит из двух перепутанных кубитов, а вторая – из независимого кубита, то состояние называется бисе-парабельным. Состояния, которые не являются ни сепарабельными, ни бисепарабельными, называются истинно перепутанными. Для трех-кубитных систем существуют два типа истинно перепутанных состояний, которые представляют собой так называемые состояния GHZ- и W-типа. Для трехкубитных смешанных состояний также существуют сепарабельные, бисепарабельные или истинно запутанные состояния. Если тип чистого состояния многокубитной системы определяется свойствами вектора состояния, то для смешанных состояний аналогичные свойства должны выполняться для выпуклой суммы чистых состояний. Перепутанные состояния трехкубитных систем можно использовать для квантовой обработки информации, детерминированной телепортации, плотного кодирования и т. д. Трехкубитные перепутанные состояния различных типов в настоящее время экспериментально реализованы для различных типов кубитов, в частности для ионов в магнитных ловушках и сверхпроводящих цепях [8; 9]. В работе [20] было предсказано, что перепутывание пары кубитов, взаимодействующих с полем резонатора, может полностью исчезнуть за времена, значительно меньшие времени декоге-ренции. Это явление получило название внезапной смерти запутанности. Позднее этот эффект для двухкубитной системы был обнаружен экспериментально [21]. Для трехкубитной системы эффект был впервые предсказан в [22]. В настоящее время изучению данного эффекта уделяется особое внимание, поскольку указанный эффект оказывает существенное влияние на динамику систем кубитов, используемых в устройствах квантовой обработки информации (см. ссылки в [23]). В ряде недавних работ эффект мгновенной смерти перепутывания рассматривался для различных систем кубитов, взаимодействующих с тепловыми шумами резонаторов [12–16]. Недавно в работе [24] мы исследовали динамику перепутывания кубитов для трехкубитной модели, в которой два кубита заперты в резонаторе и взаимодействуют с модой теплового поля этого резонатора, а третий кубит находится в свободном состоянии. В частности, нами исследовались особенности проявления эффекта мгновенной смерти и рождения перепу- тывания кубитов в такой модели. Однако в указанной работе мы ограничились рассмотрением динамики модели для начального истинно перепутанного состояния кубитов W-типа. Представляет значительный интерес расширить данное исследование, включив в рассмотрение возможные начальные бисепарабельные состояния кубитов.
В настоящей работе нами найдена точная динамика трехкубитной модели, состоящей из свободного кубита и пары кубитов, резонансно взаимодействующих с модой поля идеального резонатора. Рассмотрение проведено для начальных бисепарабельных состояний кубитов и теплового шума резонатора. Точное решение использовано для расчета параметра перепутывания пар кубитов. Проведен анализ особенностей проявления эффекта мгновенной смерти перепутывания кубитов в рассматриваемой модели.
1. Модель и точное решение квантового уравнения Лиувилля
Рассмотрим модель, которая состоит из трех одинаковых кубитов Q 1 , Q 2 и Q 3 . Пусть два кубита Q 2 и Q 3 находятся внутри резонатора и резонансно взаимодействуют с его квантованным электромагнитным полем, а первый кубит Q 1 может свободно перемещаться вне резонатора. Гамильтониан взаимодействия такой системы в стандартных приближениях имеет вид
H int = ъ1 ( a + d + a - a + ) .
i = 2
где a ± - повышающий и понижающий операторы в i -м кубите; d и d + - операторы уничтожения и рождения фотонов в моде резонатора; у - константа кубит-фотонной связи.
В качестве начальных состояний кубитов выберем бисепарабельные состояния:
| ^1 (0) > = cos a | +, -, -) + sin a | -, +, -),
| ^2 (0) > = cos a | +, -, +) + sin a | -, +, +).
В качестве начального состояния поля резонатора определим тепловое состояние с матрицей плотности вида
PF (0) = S Pn | n >< n |.
n
Здесь pn – весовые коэффициенты:
n n
Pn = где n – среднее число тепловых фотонов, которое задается следующей формулой:
n = ( exp [ h® cav I k B T ] — 1 ) 1 .
Здесь kB – постоянная Больцмана; T – температура резонатора; го cav - частота резонатора.
Найдем решение квантового уравнения Лиувилля для начальных состояний кубитов (2) и (3) и теплового состояния поля резонатора. Для каждого начального состояния кубитов мы вначале вычислим временную волновую функцию для фоковско-го начального состояния поля | n > , где n = 0 , 1 , 2 ..., а затем обобщим полученное решение на случай теплового поля. Для чистых начальных состояний кубитов и чистого фоковского состояния поля рассматриваемая система в каждый момент времени также будет находиться в чистом состоянии. Поэтому состояние системы в произвольный момент времени t можно будет задать волновой функцией | у n ( t ) > . Временная волновая функция «три кубита + мода поля» подчиняется уравнению Шредингера, которое в картине взаимодействия может быть записано как:
+ z4 (t) | 0,0,0,2), где
1 (t ) =
—
i cos a sin ( V2 Y t )
3 ’
i cos a sin ( V2 Y t )
zl (t ) =
—
i sin (V6 y t ) sin a
12 z 3 ( t ) = — sin a sin
,
^7 t ,
i sin (V6 y t ) sin a
.
12 z 2 ( t ) = sin a cos
Y t ,
i s j = « J* n ( t ) > •
Заметим, что решение уравнения Шредингера (5) для каждого из начальных состояний кубитов необходимо искать независимо для различных чисел фотонов в моде.
Рассмотрим начальное бисепарабельное состояние кубитов (2). В рассматриваемом случае решение уравнения (5) для числа фотонов в моде n = 0 можно определить как
Наконец, для n > 2 имеем:
| У n > 2 ( n , t ) ) = X 1 ( n , t ) 1 1 , 1 , 1 , n — 2) +
+ X 2 ( n , t ) 1 1 , 1 , 0 , n — 1) + X 3 ( n , t ) 1 1 , 0 , 1 , n — 1) +
+ X 4 ( n , t ) 1 1 , 0 , 0 , n ) + Y 1 ( n , t ) | 0 , 1 , 1 , n — 1) +
+ Y 2 1 ( n , t ) | 0 , 1 , 0 , n ) + Y 3 1 ( n , t ) | 0 , 0 , 1 , n ) +
+ Y1(n, t) | 0,0,0, n +1), где
X 1 ( n , t ) =
cos a sin 2
L I 11
| У n = 0 ( t ) >= cos a | + , — , — , 0) +
+ y3 (t) | —,—,—,1), где
X 3 ( n , t ) = —
1 — 2 n i4n cos a sin (y144n — 2) V 4 n — 2
i4n cos a sin ( y 14 4 n — 2 ) 4 4 n — 2
sin a ,
n — 1 + n cos
X4 (n, t )=(-------------:
2 n — 1
cos a
—j= I sin a ,
i4n sin a sin ( y 14 4 n + 2 )
i sin ( T2 y t )
У 3 ( t ) =--k=—“ sin a .
Для числа фотонов в моде n = 1 щее решение принимает вид
соответствую-
I У n = 1 ( t ) ) = x 1 ( t ) 1 1 , 1 , 0 , 0) + x 2 ( t ) 1 1 , 0 , 1 , 0) + + x 1 ( t ) 1 1 , 0 , 0 , 1) + z 1 ( t ) | 0 , 1 , 1 , 0) + + z 2 ( t ) | 0 , 1 , 0 , 1) + z 3 ( t ) | 0 , 0 , 1 , 1) +
4 4 n + 2
Y 2 ( n , t ) = sin a
cos
, 2 .
I 1 1
Y t 7+2 ,
y t4n +2 , 7
sin a sin ( y 14 4 n + 2 )
4 4 n + 2
В случае сепарабельного начального состояния кубитов (3) соответствующее решение уравнения (5) есть:
- для n = 0
Y 2 ( n , t ) =
Y 32 ( n , t ) =
—
—
sin a sin ( y 14 4 n +6 )
|
I V n = 0 ( t ) ) = x 2 ( t ) 1 |
1 , 1 , 0 , |
0) + x 2 ( t ) I |
1 , 0 , 1 , 0)+ (12) |
|
|
+ x 3 ( t |
) 1 1 , 0 , 0 , 1) + |
z 2 ( t ) |
I 0 , 1 , 1 , 0) + |
|
|
+ z 2 ( t |
) I 0 , 1 , 0 , 1) + |
z 2 ( t ) I |
0 , 0 , 1 , 1) + |
|
|
+ z 4 ( t |
) I 0 , 0 , 0 , 2) , |
|||
|
где |
||||
|
x 2 ( t ) = |
= — cos a sin' |
2 fi t. к 72 |
1 ’ |
(13) |
|
x 2 ( t ) = |
= cos a cos 2 |
(л 1 172 J |
, x 3 ( t ) = - |
i cos a sin ( V2 Y t ) •------------------------------------------------------------------------------------------------- 72 ’ |
4 4 n +6
i4n +1 sin a sin ( y 14 4 n + 6 ) 4 4 n +6
2 4n +1 4n + 2 sin a sin 2
Y 42 ( n , t ) =
2 n + 3
z 2 ( t ) =1^2 + C0S ( ^^ t ) ) s i n a ’
Z 2 2 ( t ) =
—
i sin a sin ( 46t )
76 ,
z 3 ( t ) =
—
i sin a sin ( 461 )
76 ,
z 2 ( t ) =^ V2 sin a ( cos ( 46y t ) — 1 ) ;
–
для n >1
1 v n > 1 ( n , t ) )= X 2 ( n , t ) 1 + , + , + , n —1)+
+ X 2 ( n , t ) I + , + , — , n ) + X 3 ( n , t ) I + , — , + , n ) +
+ X 4 ( n , t ) I + , — , — , n +1) + Y i ( n , t ) I — , + , + , n ) +
+ Y 2 ( n , t ) I — , + , — , n +1) + Y 3 ( n , t ) I — , — , + , n +1) +
+ Y 4 ( n , t ) I — , — , — , n + 2) ,
где
i4n cos a sin ( y 14 4 n + 2 )
X 1 ( n , t ) = /
V 4 n + 2
f
X 2 ( n , t ) = — cos a sin 2
к
I 11
Y 4n +2 , 7
f
X 3 ( n , t ) = cos a cos2 '
к
, I 11 Y 4n +2 , . 7
X 4 ( n , t ) = —
cos a sin ( y 14 4 n + 2 )
4 4 n + 2
Y 12 ( n , t ) =
sin a ( n + 2 + ( n +1 ) cos ( y 14 4 n +6 ) ) 2 n + 3
' \ 3
Y 4n + 2
к
к
Теперь, зная явный вид волновых функций благодаря выражениям (6)–(15), можно построить матрицу плотности полной системы «три кубита + мода поля» для теплового состояния поля резонатора:
p Q^QF (t) = E Pn I V n (t )Xv n (t) I-
Матрица плотности (13) для начального состояния (2) может быть переписана в виде
PQQQF ( t ) = Z Pn I Vn>2 (n, t)XVn>2 ( n, t ) I + n=2
+ P1 I Vn=1 (t))
S
P QQQF ( t ) = £ P n I V n > 1 ( n , t )X v n > 1 ( n , t ) I + (18)
123 n = 1
+
P
0 I
V
n
=
0
(
t
)
)
2. Вычисление отрицательности
Для вычисления любых известных критериев перепутывания трехкубитной подсистемы необходимо вычислить редуцированную матрицу плотности трех кубитов следующим образом:
P Q i Q o Q o = Tr F P QQQ^ ’ (19)
123 123
При исследовании динамики перепутывания кубитов для бисепарабельных начальных состояний (2) и (3) наиболее информативным критерием
перепутывания является отрицательность пар кубитов [25; 26]. Для нахождения указанного параметра необходимо вычислить редуцированную матрицу плотности соответствующей пары кубитов:
P QQ-ij
= Tr k P Q 1 Q 2 Q 3 ( i , j , k = 12 , 3 ;
i ^ j ^ k ) .
Определим критерий отрицательности стан-
дартным образом:
^j^ h). —•
где v j - отрицательные собственные значения частично транспонированной по переменным одного кубита редуцированной двухкубитной матрицы
|
плотности |
T P QiQj |
( t ) , которая имеет для |
состояний |
|
|
(2)-(3) следу p QQ . ( t ) = ij |
ющий вид: QiQj . „ Г QiQj P 11 0 0 1 P 23 0 P 22 Qj 0 0 |
. (21) |
||
|
0 q- XP 23 |
0 P 33 j 0 0 0 P 44 j |
; |
||
Для состояния (2) и кубитов Q 1 и Q 2 элементы матрицы плотности (21) выражаются следующим образом:
QQ / \ “
P111 2 (t) = Z Pn n=2
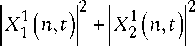
QQ / \ S P 33 1 3 ( t ) = Z P n n = 2
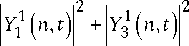
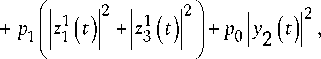
QQ i \ S P 44 1 3 ( t ) = Z P n n = 2
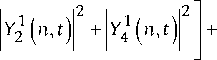
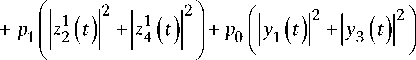
+ P 1 I х 1 ( t )|
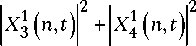
P Q 31 Q 3 ( t ) = Z P n [ X 21 ( n , t ) Y 1 ( n , t ) + n = 2
+ X 4 ( n , t ) y 1 ( n, t ) ]+ P 1 ( x 1 ( t ) z 1 ( t ) + x 3 ( t ) z 3* ( t ) ) +
+ P 0 cos a y 2 ( t ) .
Для состояния (2) и кубитов Q 2 и Q 3 элементы матрицы плотности (21) выражаются следующим образом:
QQ i \ “
P 221 2 ( t ) = Z P n n = 2
+ P 1
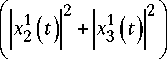
+ P 0 cos
a ,
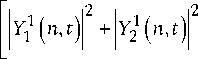
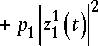
QQ I \ S P 112 3 ( t ) = Z P n n = 2
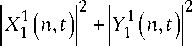
P QQ 2 ( t ) =Z P n n = 2
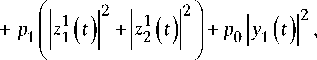
QQ i \ “
P441 2 (t) = Z Pn n=2
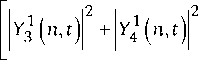
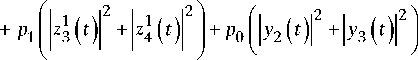
P Q3Q 2 ( t ) = Z P n [ X 4 ( n , t ) Y2* ( n , t ) + n = 2
+ X 3 ( n , t ) Y f ( n, t ) ] + P 1 ( x 1 ( t ) z f ( t ) + х 1 ( t ) z 1* ( t ) ) + p 0 cos a y 1 ( t ) .
|
P Q 22 Q 3 ( t ) = |
S Z Pn |
1 X t ) |
'21 ( n , t ) + 2 X , J + p 0 y 1 |
Y 21 ( n , t ) t ) 2 , |
2 |
+ |
||
|
+ p 1 [ |
x 1 ( t ) |
n = 2 2 + |
z 2 1 |
|||||
|
P 33 2 3 |
( t ) = |
S Z Pn |
X |
3 ( n , t ) + |
Y 1 ( n , t ) |
2 ' |
+ |
|
|
n = 2 |
- |
|||||||
|
+ p 1 [ |
x 2 ( t ) |
2 + |
z 3 1 |
( t ) |
j + P 0 y 2 ( t ) 2 , |
|||
|
P 44 2 3 |
( t ) = |
S Z Pn n = 2 |
X |
r4 ( n , t ) + |
Y 4 ( n , t ) |
2 ■ |
+ |
|
Для состояния (2) и кубитов Q 1 и Q 3 элементы матрицы плотности (18) есть:
+ P 1
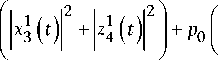
2 cos a +
QQ / \ ®
P111 3 (t) = Z Pn n=2
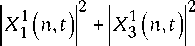
P Q 2 Q 3 ( t ) = Z P n [ X 2 ( n , t ) X 3* ( n , t ) + n = 2
+ P 1 | x 2 ( t )|
+ P 1
QQ / \ ®
P 22 1 3 ( t ) = Z P n n = 2
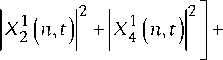
+ Y 21 ( n , t ) Y 1* ( n , t ) ] + P 1 ( x 11 ( t ) x 2* ( t ) + z 2 ( t ) z 3* ( t ) ) +
+ p 0 y 1 ( t ) y 2 ( t ) .
Для состояния (3) и кубитов Q 1 и Q 2 элементы матрицы плотности (21) определяются как
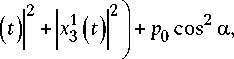
QQ / \ “
Pn1 2 (t) = Z Pn n=1
|
+ P 0 ; |
( 2( t ) 2 , |
P 11 2 3 |
S ( t ) = Z P n n = 1 |
1 X 2 ( n , t ) 2 + |
Y ,2 ( nt )2 |
+ |
||
|
P 22 12 |
® ( t ) = Z p n n = 1 |
1 X 3 ( n . t )| 2 +| X 42 ( nt )| |2 |
1* |
+ P 0 z |
2 ( t ) 2 , |
- |
||
|
+ P 0 ^ |
x 2 ( t ) 2 + x 3 |
1 t ) 2 ] ’ |
P 22 2 3 |
S ( t ) = Z p n n = 1 |
I X 22 ( n.t )| 2 + |
Y ( nt 1 2] |
+ |
|
|
P 33 12 |
“ ( t ) =Z P n n = 1 |
Y 1 2 ( n , t ) 2 + Y 2 2 ( n , t ) 2 |
+ |
+ P 0 ^ |
x 1 2 ( t ) 2 + z 2 |
( t ) ] ’ |
||
|
+ P 0 ^ |
z 2 ( t ) 2 + z 2 2 |
( t ) 2 ] ’ |
P 33 2 3 |
S ( t ) = Z p n n = 1 |
I X 3 2 ( n , t )| 2 + |
Y ( nt )|2 ] |
+ |
|
|
P 44 12 |
“ ( t ) =Z P n n = 1 |
Y 3 2 ( n , t ) 2 + Y ( n , t ) 2 |
+ |
+ P 0 ^ |
x 2 ( t ) 2 + z 3 |
( t ) ] ’ |
||
|
+ P 0 ^ |
z 3 ( t ) + z 4 |
( t ) 2 ] ’ |
P 44 2 3 |
S ( t ) = Z p n n = 1 |
|X 44 n„ t )| 2 + |
Y 4 ( nt ) 4 |
+ |
|
|
P 23 12 |
S 1 t ) = Z P n n = 1 |
X 4 ( n , t ) Y 2* ( n , t ) + |
+ P 0 ^ |
x 3 ( t ) 2 + z 4 |
( t ) ] ’ |
|||
|
+ X 3 2 ( |
n , t ) Y 3 ( n , t |
) ] + P 0 ( x 2 ( t ) z 1 2 * ( t ) + x 3 |
( t ) z 2* ( t ) ) • |
P 23 2 3 |
S 1 t ) = Z P n n = 1 |
X 2 2 ( n , t ) X 3* |
( n ,t ) + |
Для состояния (3) и кубитов Q 1 и Q 3 элементы матрицы плотности (21) имеют вид
QQ / \ ® n=1
+ p 0 | x 2 ( t )| ,
I X 22 ( n , t )| 2 +| X 3 ( n , t )| 2
+
+ Y 22 ( n , t ) Y 3 ( n , t ) ] + P 0 ( x l ( t ) x 2* ( t ) + z 2 ( t ) z 3* ( t ) ) •
Для всех рассматриваемых случаев матрица плотности (21) имеет всего одно собственное значение, которое может быть меньше нуля. В этом случае формула для отрицательности (20) принимает вид
QQ / \ S Р 221 3 ( t ) = Z P n n = 1
|X 22 ( n , t )| 2 +| X 4 ( n , t )| 2
Q i Q
P 44'
^^^B
Q i Q
P 11 '
2 Q i Q j
^^^B
QQ QQ
P 11H -P 44 7 • (22)
+ p 0
QQ ( \ S P 33 1 3 ( t ) = Z P n n = 1
I Y 12 ( n , t ) 2 + | Y 32 ( n , t )| 2
+ p 0
QQ / \ ®
P441 3 (t) = Z Pn n=1
| Y2 ( n , t ) 2 + Y 4 ( n , t )| 2
+
+
+ p 0
n = 1
+ X 4 ( n , t ) Y 3 2 * ( n , t ) ]+ p 0 ( x i 2 ( t ) z 1 2 * ( t ) * x 3 ( t ) z 3* ( t ) ) •
Для состояния (3) и кубитов Q 2 и Q 3 элементы матрицы плотности (21), соответственно, есть:
Результаты численных расчетов отрицательности пар кубитов (22) для начальных бисепарабель-ных состояний (2) и (3) представлены на рис. 1–4.
3. Результаты и обсуждение
На рис. 1, a показана зависимость параметра перепутывания S 12 для кубитов Q i и Q 2 от безразмерного времени у t для бисепарабельного начального состояния кубитов (2) с а = п / 4 и различных значений среднего числа фотонов в моде резонатора. Для сравнения, на рис 1, б представлены аналогичные зависимости для модели, состоящей из трех кубитов, запертых в одномодовом резонаторе и резонансно взаимодействующих с выделенной модой поля (соответствующие формулы для отрицательностей представлены в нашей предыдущей работе [27]). При усреднении по состояниям третьего кубита состояния кубитов Q 1 и Q 2 в начальный момент времени максимально
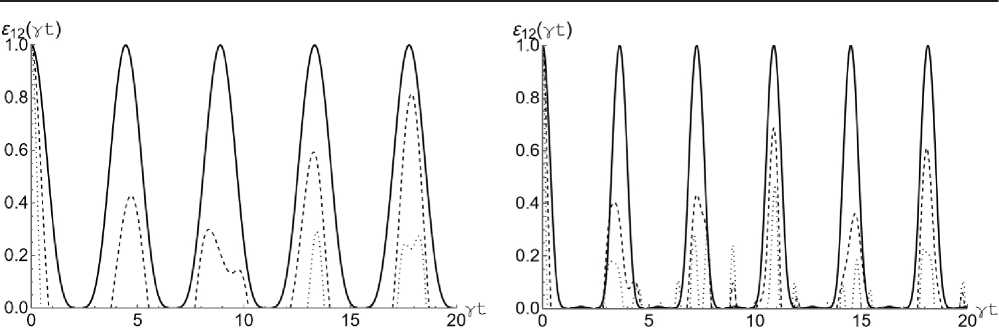
Рис. 1. Графики зависимости критерия отрицательности е.^ ( y t ) от приведенного времени y t для начального бисепарабельного состояния (2) с изменением среднего числа тепловых фотонов n в модели с двумя кубитами в резонаторе ( а ) и с тремя кубитами в резонаторе ( б) при а = п / 4. На обоих графиках: n = 0,0001 (сплошная линия), n = 1 (пунктирная линия), n = 4 (точечная линия) Fig. 1. Graphs of the dependence of the negativity criterion е 12 ( y t ) on the reduced time y t for the initial biseparable state (2) with achange in the average number of thermal photons n in the model with two qubits in the resonator ( a ) and with three qubits in the resonator ( b ) at a = n /4. On both graphs: n = 0,0001 (solid line), n = 1 (dashed line), n = 4 (dotted line)
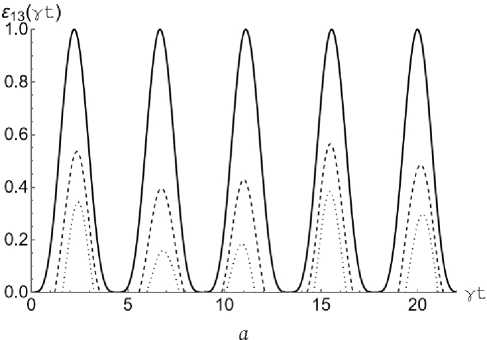
Рис. 2. Графики зависимости критерия отрицательности е 1з ( y t ) от приведенного времени y t для начального бисепарабельного состояния (2) с изменением среднего числа тепловых фотонов n в модели с двумя кубитами в резонаторе ( а ) и с тремя кубитами в резонаторе ( б ) при а = п /4. На обоих графиках: n = 0,0001 (сплошная линия), n = 0,5 (пунктирная линия), n = 1 (точечная линия) Fig. 2. Graphs of the dependence of the negativity criterion е 13( y t ) on the reduced time y t for the initial biseparable state (2) with achange in the average number of thermal photons n in the model with two qubits in the resonator ( a ) and with three qubits in the resonator ( b ) at a = n /4. On both charts: n = 0,0001 (solid line), n = 0,5 (dashed line), n = 1 (dotted line)
б
перепутаны. Этому соответствует начальное значение е12 = 1. Из рисунка хорошо видно, что на некоторых временах перепутывание резко исчезает и остается нулевым в течение конечного времени, прежде чем возродиться. Это означает наличие в системе эффекта мгновенной смерти перепутывания. Из рисунка также видно, что с увеличением среднего числа тепловых фотонов максимальная степень перепутывания кубитов быстро уменьшается. Важно отметить, что эффект мгновенной смерти перепутывания отсутствует в случае малых интенсивностей теплового поля (n ^ 0) при любых значениях начального параметра α как в модели с двумя кубитами в резонаторе, так и с тремя. С увеличением числа тепловых фотонов в моде промежутки времени, для которых в системе отсутствует перепутывание, увеличиваются. Отличие в поведении отрицательности для модели трех кубитов, запертых в резонаторе, сводится к уменьшению периода осцилляций и увеличению времени смерти перепутывания. На рис. 2, a показана зависимость параметра перепутывания ε13 для кубитов Q1 и Q3 от безразмерного времени γt для бисепарабельного начального состояния кубитов (2) с а = п / 4 и различных значений теплового поля резонатора. Соответственно, на рис. 2, б показаны аналогичные зависимости для модели с тремя кубитами в резонаторе. В отличие от предыдущего случая, в начальный момент времени пара кубитов Q1 и Q3 находится в сепарабельном состоянии, что соответствует начальному значению е13 = 0.
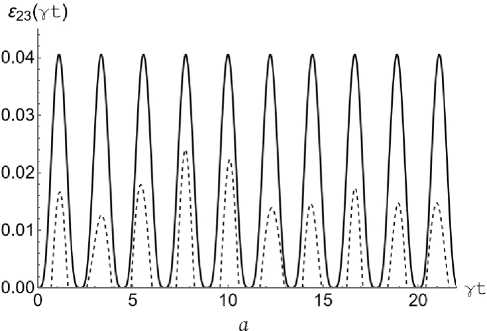
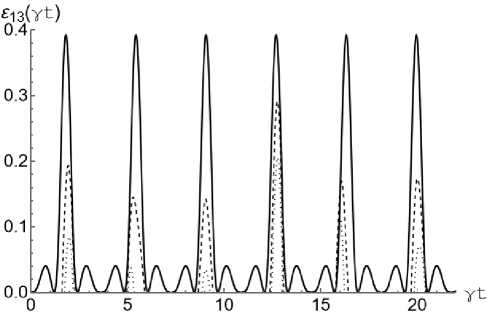
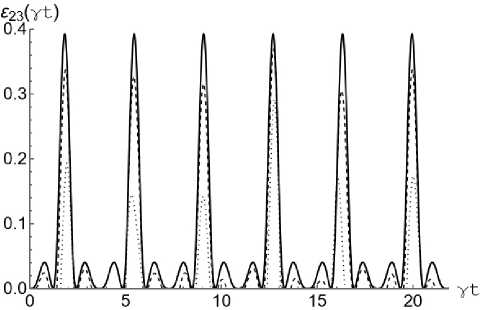
Рис. 3. Графики зависимости критерия отрицательности £ 23 ( у t ) от приведенного времени у t для начального бисепарабельного состояния (2) с изменением среднего числа тепловых фотонов n в модели с двумя кубитами в резонаторе ( а ) и с тремя кубитами в резонаторе ( б при а = п / 4. На графиках обоих: n = 0,0001 (сплошная линия), n = 0,1 (пунктирная линия), n = 0,5 (точечная линия)
Fig. 3. Graphs of the dependence of the negativity criterion £ 23 ( у t ) on the reduced time у t for the initial biseparable state (2) with a change in the average number of thermal photons n in the model with two qubits in the resonator ( a ) and with three qubits in the resonator ( b ) at a = n /4. On both graphs: n = 0,0001 (solid line), n = 0,1 (dashed line), n = 0,5 (dotted line)
б
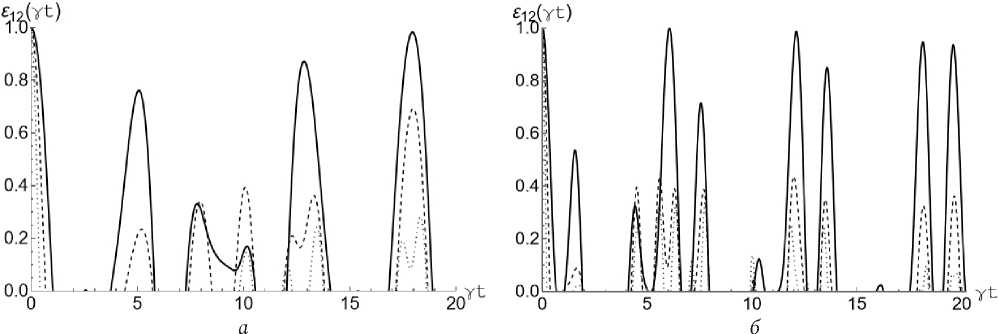
Рис. 4. Графики зависимости критерия отрицательности £ 12 ( у t ) от приведенного времени у t для начального бисепарабельного состояния (3) с изменением среднего числа тепловых фотонов n в модели с двумя кубитами в резонаторе ( а ) и с тремя кубитами в резонаторе ( б при а = п / 4. На обоих графиках: n = 0,0001 (сплошная линия), n = 1 (пунктирная линия), n = 4 (точечная линия) Fig. 4. Graphs of the dependence of the negativity criterion £ 12 ( y t ) on the reduced time у t for the initial biseparable state (3) with achange in the average number of thermal photons n in the model with two qubits in the resonator ( a ) and with three qubits in the resonator ( b ) at a = n /4. On both graphs: n = 0,0001 (solid line), n = 1 (dashed line), n = 4 (dotted line)
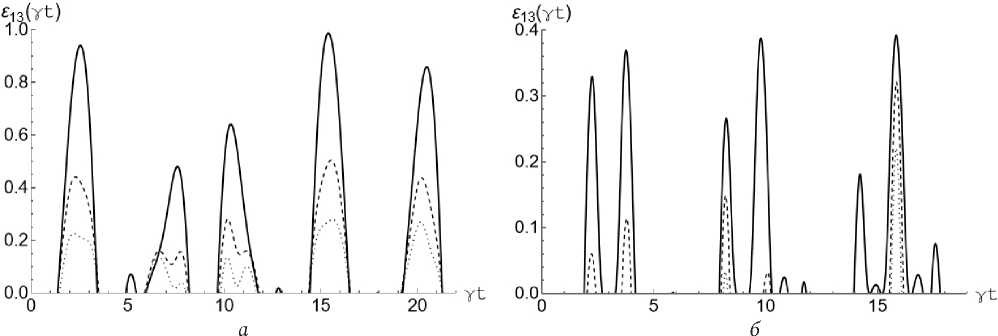
Рис. 5. Графики зависимости критерия отрицательности £ 13 ( у t ) от приведенного времени у t для начального бисепарабельного состояния (3) с изменением среднего числа тепловых фотонов n в модели с двумя кубитами в резонаторе ( а ) и с тремя кубитами в резонаторе ( б при а = п /4. На обоих графиках: n = 0,0001 (сплошная линия), n = 0,5 (пунктирная линия), n = 1 (точечная линия) Fig. 5. Graphs of the dependence of the negativity criterion £ 13 ( у t ) on the reduced time у t for the initial biseparable state (3) with a change in the average number of thermal photons n in the model with two qubits in the resonator ( a ) and with three qubits in the resonator ( b ) at a = n /4. On both graphs: n = 0,0001 (solid line), n = 0,5 (dashed line), n = 1 (dotted line)
Максимальная степень перепутывания кубитов для модели с тремя кубитами в общем резонаторе существенно меньше соответствующей величины для модели с двумя кубитами в резонаторе. Остальные выводы, касающиеся поведения отрицательности пары кубитов Q i и Q 2 , для обеих рассмотренных моделей оказываются справедливыми и для кубитов Q i и Q 3 . На рис. 3, a показана зависимость параметра перепутывания ε23 для кубитов Q 2 и Q 3 от безразмерного времени γ t для бисепарабельного начального состояния кубитов (2) с а = п / 4 и различных значений среднего числа фотонов в моде резонатора. Для сравнения, на рис. 3, б представлены аналогичные зависимости для модели, состоящей из трех кубитов в общем резонаторе. Аналогично предыдущему случаю в начальный момент времени пара кубитов Q 1 и Q 3 находится в сепарабельном состоянии. На рис. 3 хорошо видно, что максимальная степень перепутывания кубитов Q 2 и Q 3 для рассматриваемой модели на порядок меньше аналогичной величины для модели с тремя кубитами в резонаторе. Интересной особенностью динамики перепутывания кубитов Q 2 и Q 3 выбранного бисепарабельного состояния (2) является отсутствие какого-либо перепутывания даже при относительно небольших значениях интенсивности теплового поля, в то время как в модели с тремя кубитами в резонаторе с той же интенсивностью теплового поля перепутывание для данной пары наблюдается.
На рис. 4, a построена зависимость параметра перепутывания ε12 для кубитов Q 1 и Q 2 от безразмерного времени γ t для бисепарабельного начального состояния кубитов (3) с а = п / 4 и различных значений среднего числа фотонов в моде резонатора. Для сравнения, на рис. 4, б представлены аналогичные зависимости для модели, состоящей из трех кубитов в общем резонаторе. При усреднении по состояниям третьего кубита, как и в случае начального состояния (2), кубиты Q 1 и Q 2 в начальный момент времени максимально перепутаны. Сравнение рис. 1 и 4 выявляет, что для начального состояния кубитов (3) существенно возрастает длительность временных интервалов, на которых состояния кубитов распутаны, а также присутствует эффект мгновенной смерти перепутывания даже в случае малых интенсивностей теплового поля. На рис. 5, a отражена зависимость параметра перепутывания ε13 для кубитов Q 1 и Q 3 от безразмерного времени γ t для бисе-парабельного начального состояния кубитов (3)
с а = п / 4 и различных значений интенсивностей поля резонатора. Видно, что в случае малых интенсивностей теплового поля присутствует эффект мгновенной смерти перепутывания в отличие от аналогичной пары кубитов для начального состояния (2). На рис. 5, б приведены аналогичные зависимости для модели с тремя кубитами в резонаторе. Для рассматриваемых кубитов Q 1 и Q 3 начальное состояние является сепарабельным, для которого S 13 = 0 . Для состояния (3) максимальная степень перепутывания кубитов для модели с тремя кубитами в общем резонаторе также существенно меньше соответствующей величины для модели с двумя кубитами в резонаторе. Для кубитов Q 1 и Q 3 существенно возрастают промежутки времени, для которых перепутывание кубитов Q 1 и Q 3 отсутствует. Наиболее интересными представляются расчеты отрицательности пары кубитов Q 2 и Q 3 для начального бисепарабельно-го состояния (3). Указанные расчеты указывают на отсутствие в рассматриваемой модели перепутывания кубитов в процессе их эволюции при любых интенсивностях теплового поля. В то время как для модели с тремя кубитами в общем резонаторе поведение отрицательности тех же кубитов Q 2 и Q 3 полностью аналогично поведению отрицательности кубитов Q i и Q 3 .
Заключение
В настоящей работе мы исследовали динамику системы трех идентичных кубитов, два из которых заперты в идеальном резонаторе и резонансно взаимодействуют с модой электромагнитного поля этого резонатора, а третий кубит находится в свободном состоянии. Получено точное решение квантового уравнения Лиувилля рассматриваемой модели для начальных бисепарабельных состояний кубитов и теплового поля резонатора. На основе точного решения рассчитаны отрицательности всех пар кубитов. Расчеты проведены для двух типов бисепарабельных состояний и тепловых состояний электромагнитного поля резонатора для различных средних чисел фотонов. Проведено также сравнение динамики перепутывания кубитов для рассматриваемой модели и модели, в которой три кубита заперты в общем резонаторе. Показано, что тепловое поле резонатора не разрушает полностью начальное перепутывание пар кубитов даже для относительно высоких интенсивностей теплового шума резонатора. Для сепарабельных состояний кубитов взаимодействие с тепловым полем индуцирует их перепутывание в процессе эволюции. Отмечено, что для больших интенсивностей теплового поля резонатора имеет место эффект мгновенной смерти перепутывания. Указанный эффект отсутствует только для начального бисепарабельного состояния (2) для всех пар кубитов в случае малых интенсивностей теплового поля при любых значениях начального параметра α. Расчеты также показали, что продолжительность промежутков времени между мгновенной смертью и возобновлением перепутывания кубитов существенно зависит от выбора начального бисепарабельного состояния кубитов.
Список литературы Динамика перепутывания кубитов в трехкубитной модели Джейнса - Каммингса для бисепарабельных начальных состояний
- Georgescu I.M., Ashhab S., Nori F. Quantum simulation // Reviews of Modern Physics. 2014. Vol. 88. P. 153–186. DOI: https://doi.org/10.1103/RevModPhys.86.153
- Superconducting qubits: Current state of play / M. Kjaergaard [et al.] // Annual Reviews of Condensed Matter Physics. 2020. Vol. 11. P. 369–395. DOI: https://doi.org/10.1146/annurev-conmatphys-031119-050605
- Superconducting quantum computing: A review / H.-L. Huang [et al.] // Science China Information Sciences. 2020. Vol. 63. P. 180501. DOI: https://doi.org/10.1007/S11432-020-2881-9
- Shi J. Entanglement research for the coupled superconducting phase qubit and a two-level system // Advances in Condensed Matter Physics. 2020. Vol. 2020. P. 3838106. DOI: https://doi.org/10.1155/2020/3838106
- Quantum entanglement / R. Horodecki [et al.] // Reviews of Modern Physics. 2009. Vol. 81, no. 2. P. 865–942. DOI: https://doi.org/10.1103/RevModPhys.81.865
- Bruss D., Leuchs G., Quantum Information: From Foundations to Quantum Technology Applications. Cambridge: Wiley-VCH, 2019. 892 p.
- Luo M.-X., Fe S.-M. Genuinely multipartite entanglement vias shallow quantum circuits // Advanced Quantum Technologies. 2023. Vol. 6, no. 2. P. 2200089. DOI: https://doi.org/10.1002/qute.202200089
- Generation of three-qubit entangled states using superconducting phase qubits / M. Neeley [et al.] // Nature. 2010. Vol. 467, no. 7315. P. 570–573. DOI: https://doi.org/10.1038/nature09418
- Dissipative preparation of W states in trapped ion systems / D.C. Cole [et al.] // New Journal of Physics. 2021. Vol. 23, no. 7. P. 073001. DOI: https://doi.org/10.1088/1367-2630/ac09c8
- Gühne O., Tôth G. Entanglement detection // Physics Reports. 2009. Vol. 474, no. 1–6. P. 1–75. DOI: https://doi.org/10.1016/j.physrep.2009.02.004
- Entanglement certification from theory to experiment / N. Friis [et al.] // Nature Reviews Physics. 2019. Vol. 1. P. 72–87. DOI: https://doi.org/10.1038/s42254-018-0003-5
- Башкиров Е.К. Тепловое перепутывание в двухатомной модели Тависа – Каммингса с учетом диполь-дипольного взаимодействия // Физика волновых процессов и радиотехнические системы. 2023. Т. 26, № 2. С. 9–17. DOI: https://doi.org/10.18469/1810-3189.2023.26.2.9-17
- Башкиров Е.К. Перепутывание двух сверхпроводящих кубитов, индуцированное тепловым шумом резонатора со средой Керра, при наличии начальной атомной когерентности // Физика волновых процессов и радиотехнические системы. 2022. Т.25, № 1. С. 7–15. DOI: https://doi.org/10.18469/1810-3189.2022.25.1.7-15
- Захаров Р.К., Башкиров Е.К. Влияние расстройки и керровской нелинейности на атом-атомное перепутывание в двойной двухфотонной модели Джейнса – Каммингса // Физика волновых процессов и радиотехнические системы. 2021. Т. 24, № 1. С.9–14. DOI: https://doi.org/10.18469/1810-3189.2021.24.1.9-14
- Башкиров Е.К. Перепутывание атомов, индуцированное тепловым шумом при наличии начальной атомной когерентности // Физика волновых процессов и радиотехнические системы. 2020. Т. 23, № 3. С. 10–17. DOI: https://doi.org/10.18469/1810-3189.2020.23.3.10-17
- Башкиров Е.К., Гуслянникова М.О. Перепутывание атомов с двухфотонными переходами при наличии динамического штарковского сдвига энергетических уровней // Физика волновых процессов и радиотехнические системы. 2019. Т. 22, № 3. С. 36–43. DOI: https://doi.org/10.18469/1810-3189.2019.22.3.36-43
- Filippov S.N. Quantum mappings and characterization of entangled quantum states // Journal of Mathematical Sciences. 2019. Vol. 241, no. 2. P. 210–236. DOI: https://doi.org/10.1007/s10958-019-04418-3
- Quantum fidelity measures for mixed states / Y.-C. Liang [et al.] // Reports on Progress in Physics. 2019. Vol. 82, no. 7. P. 076001. DOI: https://doi.org/10.1088/1361-6633/ab1ca4
- Ma M., Li Y., Shang J. Multipartite entanglement measures: A review // arXiv:2309.09459. 2023. P. 1–14. DOI: https://doi.org/10.48550/arXiv.2309.09459
- Yu T., Eberly J.H. Finite-time disentanglement via spontaneous emission // Physical Review Letters. 2003. Vol. 93, no. 14. P. 140404. DOI: https://doi.org/10.1103/PhysRevLett.93.140404
- Environment-induced sudden death of entanglement / M.P. Almeida [et al.] // Science. 2007. Vol. 316, no. 5824. P. 579–582. DOI: https://doi.org/10.1126/science.1139892
- Ge M., Zhu L.-F., Qui L. Three-qubit entanglement sudden death // Communications in Theoretical Physics. 2008. Vol. 49, no. 6. P. 1443–1448. DOI: https://doi.org/10.1088/0253-6102/49/6/20
- Xie S., Younis D., Eberly J.H. Evidence for unexpected robustness of multipartite entanglement against sudden death from spontaneous emission // Physical Review Research. 2023. Vol. 5, no. 3. P. L032015. DOI: https://doi.org/10.1103/PhysRevResearch.5.L032015
- Багров А.Р., Башкиров Е.К. Динамика теплового перепутывания пар кубитов в трехкубитной модели Тависа – Каммингса // Журнал технической физики. 2024. Т. 94, № 4. (Принято к печати).
- Peres A. Separability criterion for density matrices // Physical Review Letters. 1996. Vol. 77, no. 8. P. 1413–1415. DOI: https://doi.org/10.1103/PhysRevLett.77.1413
- Horodecki R., Horodecki M., Horodecki P. Separability of mixed states: Necessary and sufficient condition // Physics Letters A. 1996. Vol. 223, no. 1–2. P. 1–8. DOI: https://doi.org/10.1016/S0375-9601(96)00706-2
- Багров А.Р., Башкиров Е.К. Динамика трехкубитной модели Тависа – Каммингса // Вестник Самарского университета. Естественнонаучная серия. 2022. Т. 28, № 1–2. С. 95–105. DOI: https://doi.org/10.18287/2541-7525-2022-28-1-2-95-105


