Динамика периодических электромагнитных волн в системе углеродных нанотрубок

В последнее десятилетие большое внимание специалистов, занимающихся созданием и исследованием новых материалов – физиков, материаловедов, механиков (как теоретиков, так и экспериментаторов) – вызвали наноструктурные материалы (НСМ) 1. Эти материалы обладают уникальной структурой и свойствами, многие из которых имеют непосредственный практический интерес во многих отраслях науки и техники. Одну из ведущих ролей в качестве строительных блоков электроники XXI в. начинают играть углеродные нанотрубки с их особенными электронными и механическими свойствами. Углеродные нанотрубки (УНТ) являются уникальными макромолекулярными системами. Их весьма малый нанометровый диаметр и большая микронная длина указывают на то, что они наиболее близки по своей структуре к идеальным одномерным (1D) системам.

Вышеописанные свойства УНТ привели к их широкому изучению и применению в рамках нелинейной оптики. Одним из основных и наиболее перспективных направлений в этой области является исследование распространения в УНТ ультракоротких импульсов света (оптических солитонов) 2. Как известно 3, в качестве одной из основных целей современной оптики является создание полностью оптических приборов, в которых светом можно управлять с помощью света. Это, в свою очередь, привело к тому, что в последнее время наблюдается бурный рост исследования оптических эффектов, связанных с взаимодействием электромагнитных солитонов. Этот интерес стимулируется как успешными экспериментами, в которых получены многомерные оптические солитоны (устойчивые локализованные световые структуры), так и появлением новых материалов, являющихся достаточно перспективными для построения полностью оптических приборов. Отметим, что помимо изучения динамики распространения одиночных оптических импульсов, с которыми, собственно, и связаны оптические солитоны, в последнее время все большее внимание привлекает изучение динамики цуга импульсов или периодических нелинейных волн. Подобная ситуация может возникнуть, например, при внут-рирезонаторной методике изучения отклика вещества, когда исследуемый объект помещается внутрь кольцевого резонатора лазера. Также рассмотрение отклика вещества на воздействие на него цугом импульсов или периодическими нелинейными волнами важно при анализе реальных задач, связанных с облучением вещества излучением лазера в режиме пичковой генерации 4. Все вышесказанное и стимулировало данную работу.

Исследование электронной структуры УНТ приведено в достаточно большом количестве работ ⁵ и, как правило, проводится в рамках анализа динамики п -электронов в приближении сильной связи. Так, в рамках вышеупомянутой модели, закон дисперсии электронов, который описывает свойства графена, имеет вид ⁶:

E(p) = ±у-J 1 + 4cos(apx )cos(apy /73) + 4cos2(apy /73), где у ~ 2,7 эВ;

a = 3 b / 2 n ;

b = 0,142 нм – расстояние между соседними атомами углерода в графене;

^p = (Px , Py )•

Отметим, что разные знаки здесь относятся к зоне проводимости и валентной зоне. Для получения закона дисперсии в случае УНТ необходимо учесть способ сворачивания графеновой плоскости в цилиндр и наложить условия квантования квазиимпульса p в направлении вдоль окружности УНТ. Для УНТ типа zig-zag, свойства которых мы рассмотрим для определенности задачи, соответственно получаем:

£(/5) = +y-Jl + 4cos(op Jcos(Ki/m) + 4cos²(ts/m)» (1)

где квазиимпульс р задается как (р,, s), s = 1, 2 ... т. При построении нашей модели распространения цуга ультракоротких оптических импульсов в системе нанотрубок, в случае геометрии, представленной на рисунке 1, будем описывать электромагнитное поле импульса классически, на основании уравнений Максвелла. Так, в интересующем нас случае, при выборе калибровки как S ^{1 9}^ X           АЛ

Е =---, уравнения Максвелла с учетом с St диэлектрических и магнитных свойств УНТ 7 можно записать как:

В² А 1 Э²Й 4л- _л --7 Г—г + J ⁼⁰’ дх² с² Bt² с

причем здесь пренебрегается дифракционным расплыванием лазерного пучка в направлениях, перпендикулярных оси распространения. Вектор-потенциал А считается имеющим вид А = (О, О, А, (х, 0).

Для определения тока воспользуемся полуклассическим приближением 8, взяв закон дисперсии (1) из квантово-механической модели и опишем эволюцию ансамбля частиц классическим кинетическим уравнением Больцмана в приближении времен релаксации:

5/ q BA. Bf ₌ F_Q-f Bt c Bt Bp. т

В (3) функция распределения f- ftp,, s, 0 неявно зависит от координаты х в силу явной зависимости от х компоненты вектор-потенциала А,, следующей из (2). F_o есть равновесная функция распределения Ферми:

l + exp№)/W где Т - температура;

к_ь - постоянная Больцмана.

Время релаксации т можно оценить согласно 9 примерно как 3 х 10 13 с. При записи уравнения (3) пренебрегалось эффектами, связанными с неоднородностью электромагнитного поля вдоль оси нанотрубки (то есть в поперечном направлении по отношению к распространению периодического цуга импульсов). Заметим, что это оправдано уже введенным выше предположением о плоском характере волнового фронта лазерного импульса. Однако при этом за пределами рассмотрения данной работы остался круг вопросов, связанных с наличием подложки, на которой и выращиваются нанотрубки. Так, в частности, учет подложки может привести к наличию в данной системе аналогов поверхностных волн, рассмотрение которых явно выходит за рамки данной работы. Также учет подложки необходим и для рассмотрения круга эффектов, связанных с накоплением в ней заряда и появлением дополнительного электрического поля, направленного вдоль оси нанотрубки.

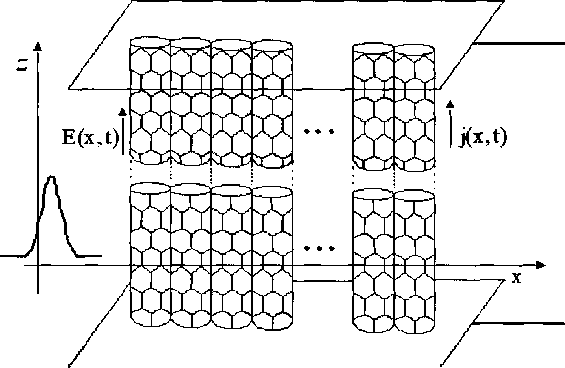
Рис. 1. Геометрия задачи

Необходимо отметить и то, что в рамках используемой нами полуклассической модели не учтены межзонные переходы, что, как показано в работе 10, дает ограничение на максимальную частоту лазерных импульсов. Так, для типичных нанотрубок, рассмотренных нами в этой работе, данная частота лежит в ближней инфракрасной области.

Уравнение (2) решается методом характеристик:

f = F 0 ( p z + ^qA z ( t )) e ^{- t / τ} + c

t

+ 1 ∫e-(t-t′)/τF0(p+q(Az(t)-Az(t′)))dt′, (4) τ -∞               c и тогда можно с учетом вышесказанного записать выражение для плотности тока j = (0, 0, jz):

j z = q ∑∫ dp z v z f ,           (5)

πη s где, как и обычно: vz

∂ p _z ^.

Выражения (2, 3, 5) составляют основ- ную систему уравнений, описывающую рас- сматриваемую нами модель.

Учитывая, что время релаксации t мало, пренебрежем первым слагаемым в (4) и сде-e лаем замену: p → p - (Az (t) - Az (t′)). Выражение для плотности тока примет вид:

t q 0 j z = ^q ∑ ∫ ∫ πητ s

-∞ - q ₀

dt ′ dp_zv_z ( p - ^q ( A_z ( t )– c

- A z ( t ′ ))) F 0 ( p r ) e ^{- ( t - t ′ )/ τ}

– A_z ( t )–

для УНТ zigzag типа интегрирование ведется по первой зоне Бриллюэна и q ₀ = ^{2 πη} . Функцию v _z ( x ) представим в виде (с учетом зависимости закона дисперсии и равновесной функции распределения F ₀ от индекса s ):

v_z ( s , x ) = ∑ a_ms sin( mx ) , m

1π ams =    vz(s, x) sin(mx)dx .

IT J

Отметим, что коэффициенты разложения a _ms убывают с ростом m , и c достаточной степенью точности можно ограничиться первыми несколькими неисчезающими слагаемыми. Конкретные данные для коэффициентов на примере УНТ типа (6, 0) можно найти в таблице 1. Для плотности тока тогда получаем:

t jz = q ∑ams ∫ dt′sin( q(Az(t)-πητms -∞ c q0

• - A z ⁽ t ‘ )) e ^{- (}t - t ‘ )/ ^T J dP z co^s( maP z ) F 0 (p ).

  - q ₀

Для исследования интеграла, содержащего временную экспоненту, воспользуемся известным в теории полупроводниковых сверхрешеток приемом ¹¹. Произведя замену ρ = t – t ′ , временной интеграл можно свести к: 0

∫ d ρ exp( -ρ / τ )sin( _c ^q ( A_z ( t -ρ ) - A_z ( t )) . Тогда, обозначая w = p / т , получаем: 0

∫ dw exp( - w ) sin( ^q ( A_z ( t - w τ ) - A_z ( t )) . Далее

• -∞                 c

необходимо учесть, что мы ищем решение в классе быстроубывающих или периодических функций. Так, приняв в учет то обстоятельство, что время τ все-таки достаточно велико при типичных длительностях ультракоротких лазерных импульсов, получаем, что A_z( t – w τ ) ≈ A _z (– ∞ ) = 0. В случае периодических граничных условий к нулю, в силу изменения знака синуса, стремит- 0

ся выражение ∫ dw exp( - w )sin _c ( A_z ( t - w τ ) . В обоих случаях ^-∞ временной интеграл приводится

Таблица 1

Коэффициенты a _ms для нанотрубок типа (6, 0) в единицах γ

	s = 1	s = 2	s = 3	s = 4	s = 5	s = 6
m = 1	–0,956	–0,849	0	0,849	0,956	0,967
m = 2	0,263	0,339	0	0,339	0,263	0,233
m = 3	–0,111	–0,218	0	0,218	0,111	0,086
m = 4	0,052	0,162	0	0,162	0,052	0,035
m = 5	–0,026	–0,127	0	0,129	0,026	0,015
m = 6	0,013	0,106	0	0,106	0,013	0,007
m = 7	–0,007	–0,091	0	0,091	0,007	0,003

к виду: sin( q Az(t)) ∫ d(-w) exp(-w). Таким c-∞ образом, эффективное уравнение можно записать в виде:

∂ ² A_z     1 ∂ ² A_z

∂ x ²

-

c ² ∂ t ²

+ q ∑cmsin(maqAz(t))=0, πητ m q0

c_m = ∑ a_msb_ms , b_ms = ∫ dp_z cos( map_z ) F ₀ ( p ) . s

- q ₀

Как показали результаты численных расчетов, коэффициенты b _ms сильно убывают с ростом m при любых температурах. При реальных же температурах (порядка комнатных), при которых проводятся исследования нанотрубок, в силу того, что Y ~ 2,7 эВ, можно воспользоваться низкотемпературным пределом для функции распределения Ферми.

Все вышесказанное приводит к тому, что вследствие убывания коэффициентов cm с ростом m в сумме в уравнении (6) можно ограничиться первыми двумя неисчезающими слагаемыми, и получить широко применяемое в приложениях, но не интегрируемое методом обратной задачи рассеяния двойное уравнение sine-Gordon 12. Важным достоинством данного уравнения есть то, что из него следует теорема площадей, а именно: устойчивы по отношению к изменению формы только импульсы, имеющие определенную «площадь» («площадь» им-∞ пульса ψ(t) определена как ∫ ψ(t)dt). Импульсы, имеющие большую «пло-∞щадь», стремятся уменьшить ее до фиксированной, а те, которые имеют меньшую «площадь», наоборот, увеличивают ее. Второе, что неоднократно 13 отмечалось исследователями двойного уравнения sine-Gordon, это то, что в случае быстро убывающих граничных условий характер взаимодействия импульсов, и главное, характер распада одиночного импульса сильно зависит от скорости. При увеличении скорости импульсы начинают взаимодействовать все более и более упруго, и меньшая часть их энергии уходит в колебательные моды.

Также необходимо отметить, что подробное исследование двойного уравнения sine-Gordon проводилось только в случае быстроубы-вающих граничных условий, и ряд особенностей эволюции начального возмущения, следующих из требования периодичности граничных условий, остался вне рассмотрения. Все это и послужило стимулом для дальнейшего численного исследования системы уравнений (2, 3, 5).

Исследуемые уравнения решались численно при помощи прямой разностной схемы типа крест. Шаги по времени и координате определялись из стандартных условий устойчивости. Шаги разностной схемы уменьшались последовательно в два раза, до тех пор пока решение не изменялось в восьмом знаке после запятой. Распространение периодического цуга импульсов при разных начальных условиях представлено на рисунке 2.

Здесь видно, что в процессе распространения, на начальном этапе, происходит появление и исчезновение лишних максимумов, то есть начальное возмущение, которое первоначально имело, например, два максимума [рис. 2 А)], в ходе эволюции приобретает дополнительный максимум, который в дальнейшем исчезает. Данное поведение можно связать с обменом энергией между разными модами, которые характеризуются разными периодами. Отметим, что в данной системе существует достаточно много мод электронных колебаний, закон дисперсии для которых задается (1). Взаимодействие между такими модами и приводит, на наш взгляд, к наблюдаемой картине. Также заметим, что подобное поведение можно связать и с периодическими решениями уравнения sine-Gordon, которые выражаются через функции Вейерштрасса 14. Взаимодействие между такими решениями, вследствие неинтегрируемости нашей системы, и дает картину, приведенную выше.

Последовательная эволюция формы периодического электромагнитного импульса при распространении в системе нанотрубок приведена на рисунке 3, а эволюция соответствующего импульса тока на рисунке 4. Моменты времени на рисунке 3 и рисунке 4 одинаковы.

Здесь необходимо обратить внимание на то, что динамика импульсов тока отстает от электромагнитного поля. Это связано с тем фактом, что проводилось моделирование динамики электронов, описываемых в рамках кинетического уравнения Больцмана с конечным временем релаксации, и электронной системе требовалось некоторое время, чтобы ее функция распределения приняла вид, требуемый полем.

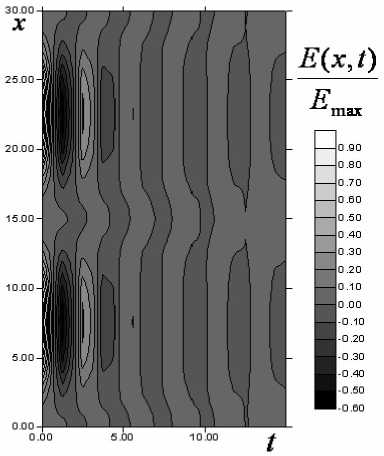
А)

Б)

Рис. 2. Распространение импульса электромагнитного поля в системе УНТ:

А), Б) – разные начальные условия. Яркость в процентах от амплитуды начального импульса, по оси абсцисс – расстояние в мкм, по оси ординат – время в единицах τ .

На рисунке Б) изменен масштаб яркости для наблюдения квазипериодического характера колебаний

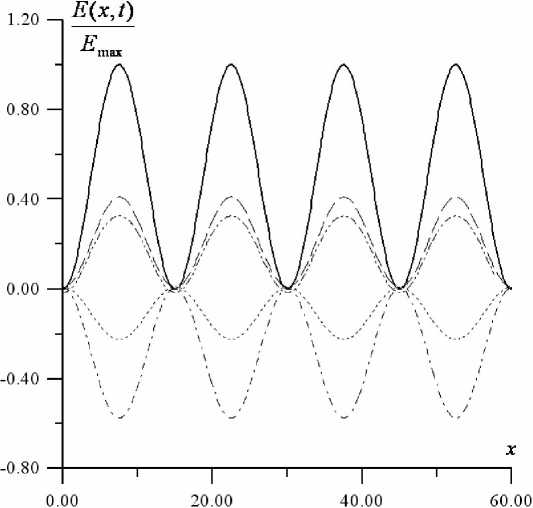
Рис. 3. Представлена эволюция формы электромагнитного импульса при распространении в системе нанотрубок (здесь и далее по оси абсцисс за единицу принят 1 мкм) для моментов времени: t = 0 (сплошная линия); t = 0,5 τ (длинный пунктир); t = 1,5 τ (точка тире);

t = 2,5 τ (две точки тире); t = 4 τ (короткий пунктир)

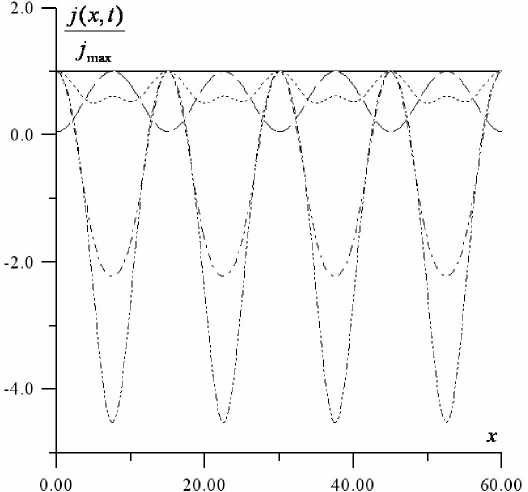
Рис. 4. Представлена эволюция формы импульса тока при распространении в системе нанотрубок.

Моменты времени те же, что и на рисунке 3

Заметим, что никаких особенностей эволюции электромагнитного импульса в зависимости от того, с какой групповой скоростью он начинал свое движение в системе нанотрубок, не наблюдалось. На наш взгляд, это связано с независимостью системы уравнений на функцию распределения электронов от скорости в явном виде и с лоренц-инвариантностью уравнений Максвелла.

При варьировании начальных условий, то есть при изменении формы цуга электромагнитных импульсов, входящих в систему УНТ, наблюдалась эволюция начальных состояний, подобно приведенной на рисунке 2. Отметим явную аналогию получившихся осциллирующих состояний с бризерными решениями уравнения sine-Gordon. Особенно сильно характер эволюции зависел, как показали результаты численных расчетов, от времени релаксации функции распределения электронов к равновесному значению.

Из проведенного исследования можно сделать следующие выводы:

• -    получена система уравнений, описывающая динамику периодической последовательности ультракоротких лазерных импульсов в системе углеродных нанотрубок, и описаны приближения, которые рассматриваются в задаче;

• -    получено эффективное уравнение для динамики электрического поля в системе углеродных нанотрубок, которое имеет вид, аналогичный двойному уравнению sine-Gordon. Оценены вклады высших гармоник, которые вносят возмущение в эффективное двойное уравнение sine-Gordon;

• -    суммарный ток, текущий через систему нанотрубок, определяется временем релаксации функции распределения электронов к равновесному значению;

• -    периодический цуг электромагнитных импульсов при прохождении системы углеродных нанотрубок проходит в ходе своей эволюции стадии, аналогичные поведению бризеров уравнения sine-Gordon;

• -    импульсы тока генерируются с запаздыванием по отношению к инициирующему импульсам электромагнитного поля, что связано с описанием динамики электронов в рамках классического кинетического уравнения Больцмана в приближении времени релаксации.