Динамика поршня двигателя внутреннего сгорания

Введение. Долговечность цилиндропоршневой группы (ЦПГ) двигателя зависит от ряда факторов, которые можно разделить на конструктивные, технологические и эксплуатационные. Конструктивные факторы являются основополагающими и в значительной мере предопределяют степень влияния всех остальных факторов на работоспособность сопряжения во время всего жизненного цикла. Поэтому более полное понимание происходящих в ЦПГ процессов еще на стадии проектирования закладывает основу для достижения более эффективной работы двигателя в целом. Основным узлом трения ЦПГ, влияющим на механические потери, является пара трения «поршень – цилиндр». От совершенства этого сопряжения зависит траектория поршня в цилиндре, тепловое состояние двигателя, количество поступающего масла к поршневым кольцам, уровень вибраций и шума. Работоспособность этой пары характеризуется зазорами между поршнем и цилиндром, профилем юбки, местом расположения пальцевого отверстия. Кроме этого, особенностью работы поршня является то, что он находится под действием крайне нестационарных тепловых и силовых факторов, в результате чего происходят тепловые и силовые деформации, приводящие к существенному изменению зазоров в сопряжении.

В рамках данной работы поршень двигателя внутреннего сгорания (ДВС) рассматривается как деформируемое материальное тело, совершающее сложное плоскопараллельное движение в пределах цилиндра. При описании этого движения, помимо усилий, действующих в кривошипношатунном механизме, учитываются также силовые факторы, возникающие при работе пары трения «поршень – цилиндр» в условиях жидкостной смазки. При этом учет гидродинамических сил и моментов производится с использованием методов, разработанных при исследовании подшипников скольжения, так как пара трения «поршень – цилиндр» представляет собой своеобразный подшипник скольжения. Величина гидродинамической реакции смазочного слоя является функцией от положения поршня в цилиндре (толщины смазочного слоя), и определяется с учетом того, что поршень деформируется в пределах цикла под действием переменных тепловых и силовых нагрузок.

Таким образом, для математического описания движения поршня в такой постановке представлена методика, основанная на совместном решении нестационарной гидродинамической задачи о распределении нормальных и касательных давлений, возникающих в зазоре, задачи определения переменного напряженно-деформированного состояния поршня и задачи динамического равновесия поршня. Данная методика включает в себя использование ряда стандартных численных методов, предусматривает применение CAD/CAE систем для решения задач определения НДС методом конечных элементов и частично опирается на результаты экспериментальных исследований.

Объект исследований. Объектом исследований является ЦПГ 4-го цилиндра двигателя ВАЗ-21083 с серийным комплектом поршней. Двигатель ВАЗ-21083 в штатном исполнении четырехтактный, бензиновый, карбюраторный с рабочим объемом 1,5 л, степенью сжатия 9,9. Номинальная мощность двигателя 51,5 кВт при частоте вращения коленчатого вала 5600 мин^–1; максимальный крутящий момент 106,4 Нм при n = 3400 мин^-1. Для смазки двигателя использовалось полусинтетическое моторное масло Esso 20W40.

В качестве расчетного режима выбран режим ( n = 3522 мин^-1; M _кр = 57,8Нм), для которого имеются результаты экспериментальных исследований динамики поршня.

Уравнения движения поршня. Движение поршня в цилиндре складывается из поступательных перемещений вдоль оси цилиндра, перемещений в плоскости, перпендикулярной оси цилиндра, а также вращения вокруг оси поршневого пальца. Для описания этого движения в рамках данной методики рассматривается динамическое равновесие (принцип Даламбера) деформи- рованного поршня, «всплывающего» на смазочном слое в пространстве зазора цилиндра двигате-

—

P трЛ

Z

* ^ГЛ

——

^р рП * ^Г П _т —

Jε

—■

P Л

—— р P трЛ

Р

FnY под

—— р P трП

——

M _П

——

M _Л

——

P П

Y

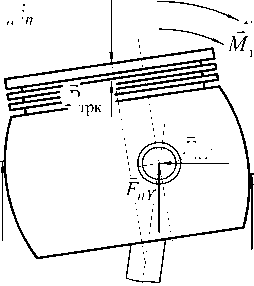
Рис. 1. Расчетная схема нагружения поршня

ля. При составлении системы уравнений динамического равновесия поршня приняты следующие допущения:

• 1)    палец с поршнем в расчете принимается как одно целое – в массово-инерционные характеристики поршня включены масса и момент инерции пальца;

• 2)    зазорами в парах «палец – шатун» и «шатун – коленчатый вал» пренебрегаем ввиду их малости;

• 3)    частота вращения коленчатого вала на расчетном режиме – постоянна;

• 4)    силы, действующие в направлении, перпендикулярном плоскости движения поршня, не рассматриваются ввиду симметричности поршня.

Осевая скорость, ускорение, боковая и инерционные силы, действующие на поршень, по всему циклу определялись из уравнений кинематики и динамики кривошипно-шатунного механизма. Индикаторная диаграмма установившегося расчетного режима работы двигателя получена пу-

тем классического расчета рабочего процесса. Таким образом, расчетная схема динамического

равновесия поршня представлена на рис. 1. Система уравнений равновесия поршня под действи-

ем приложенных сил и сил инерции имеет вид:

——         ——         ——           ——             ———

Рв + P h + R t cp + Р трк + F nZ - m n Z = 0;

——         ——         ————

Р л + Р п + F nY - m n У = 0;

——             ——                  ——                  ——           ————

РвГв + РтрпГп + РтрлГл + Mл + Mп + Мпод - Jп^п = 0, где PВ ,PН – равнодействующие давлений газа и картерных газов (соответственно сверху и снизу поршня); PП ,PЛ – равнодействующая нормальных гидродинамических сил в смазочном слое, действующих на боковую поверхность поршня (справа и слева относительно пальцевого отверстия); rВ,rН,rП,rЛ – расстояние от сил PВ ,PН ,PП ,PЛ соответственно до оси поворота (оси пальца); Rtcp – равнодействующая касательных гидродинамических сил в смазочном слое, дейст- вующих на поршень; Ртрк – сила трения между поршневыми кольцами и цилиндром; FпZ и FпY – проекции сил в опоре пальца, действующих со стороны шатуна; mп – масса поступательно движущихся частей; z - проекция на ось OZ ускорения поршня; у - проекция на ось OY ускорения поршня; PтрП, PтрЛ – равнодействующая касательных гидродинамических сил в смазочном слое, действующих на боковые поверхности поршня (справа и слева соответственно); MЛ, MП – моменты, опрокидывающие поршень, возникающие от действия нормальных гидродинамических сил в смазочном слое (справа и слева относительно пальцевого отверстия); Мпод – момент трения в подшипнике пальца; Jn - массовый момент инерции поршня (с учетом пальца); sП - угловое ускорение поршня.

Переменное напряженно-деформированное состояние поршня. Переменное напряженно-деформированное состояние поршня на расчетном установившемся режиме получено по методике [1–3] в CAD/CAE системе автоматизированного проектирования SolidWorks 2012 Cosmos. Определение НДС поршня по всему циклу двигателя предусматривало проведение двух расчетов:

• 1)    расчет температурного поля и тепловых деформаций поршня;

• 2)    расчет деформаций поршня, вызванных силовыми факторами.

В обоих расчетах использовалась объемная конечно-элементная модель серийного поршня, состоящая из 65722 тетраэдральных элементов. С целью уменьшения объемов вычислений и затрат машинного времени расчеты проводились на модели половины поршня, что допустимо ввиду симметричности.

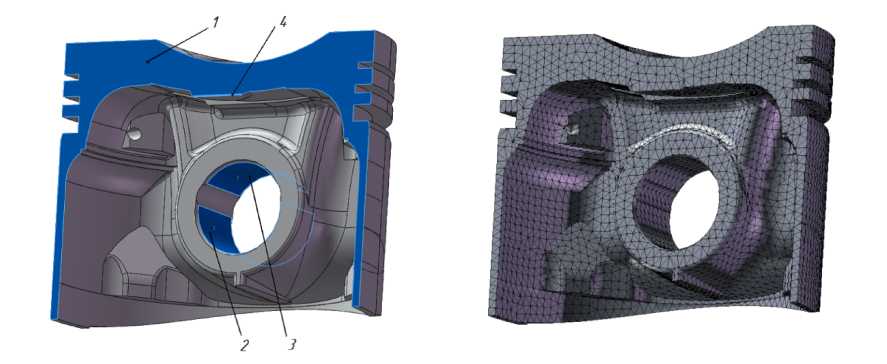
Рис. 2. Схема закрепления поршня и сетка конечных элементов

а=196 1=1000        а=20000 1=4 70

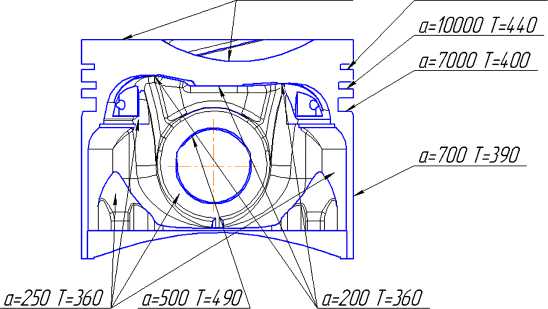
Рис. 3. Граничные условия теплообмена 3-го рода: а – коэффициент теплоотдачи, Вт/м2К; Т – температура, К

Закрепление поршня (рис. 2) осуществлялось: по поверхности 1 от перемещения перпендикулярно этой поверхности и вращений по 2 осям, перпендикулярным оси пальцевого отверстия (3 степени свободы); от радиальных перемещений относительно пальцевого отверстия по поверхностям 2 или 3 в зависимости от направления действия силы в паре «поршень – палец» (2 степени свободы); от поворота вокруг оси пальцевого отверстия – по кромке 4 (1 степень свободы).

Определение температурного поля и тепловых деформаций поршня представляло собой решение задачи теплопроводности при заданных граничных условиях. Расчет проводился в стационарной постановке при осредненных за цикл значениях граничных условий на поверхностях теплообмена.

Граничные условия 3-го рода определялись на основании расчета рабочего процесса в цилиндре на заданном режиме, а также по экспериментальным данным ПАО «АВТРАМАТ» (рис. 3). Результаты расчетов стационарного температурного поля и теплового деформированного состояния поршня представлены на рис. 4.

Расчет деформаций поршня, вызванных силовыми факторами, проводился с дискретностью по углу поворота коленчатого вала – 5°. Нагрузки, действующие на поршень, определялись по расчетной индикаторной диаграмме и из системы уравнений динамики кривошипно-шатунного механизма. При этом для каждого расчетного положения поршня вычислялось значение и знак боковой силы (или пары сил), которые равномерно распределялись по эллиптическим площадкам, выполненным на трехмерной модели поршня отдельно для каждого расчетного случая.

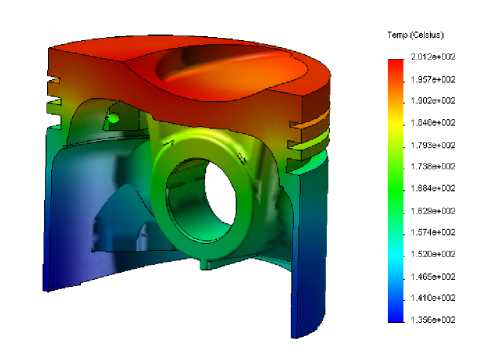
Рис. 4. Поле температур (слева) и тепловых деформаций поршня на расчетном режиме (справа)

Расположения центров эллиптических площадок (плеч приложения боковых сил) определялись по величине боковой силы и по значениям момента, вращающего поршень относительно оси пальцевого отверстия. Размеры эллиптических площадок в первом приближении определялись конструктивными соображениями (ограничения по ширине и высоте), результатами экспериментальных исследований проведенных ПАО «АВТРАМАТ» [2] и уточнялась в процессе расчетов. Таким образом, схема силового нагружения была реализована следующим образом: давление от газовых сил прикладывалось к донцу поршня, инерционная сила задавалась величиной ускорения и прикладывалась в центре тяжести, боковые силы (реакции) распределялись равномерно по эллиптическим площадкам на юбке поршня.

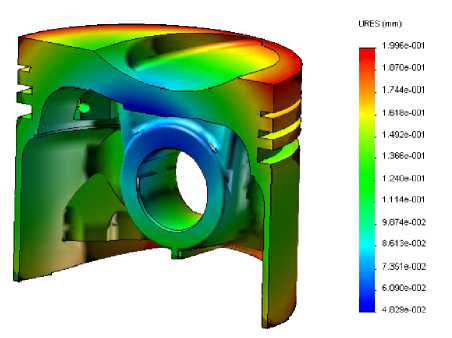
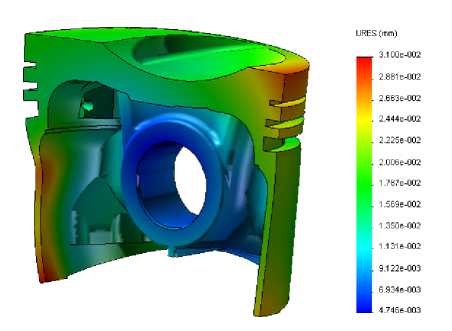
В результате расчета переменного НДС были определены деформации юбки поршня (рис. 5) в зависимости от угла поворота коленчатого вала. Эти результаты сформированы в виде 144 массивов составляющих суммарных деформаций в направлении осей OX и O Y в 48 дискретных точках поверхности юбки поршня.

Рис. 5. Поле деформаций поршня под действием силовых факторов в кривошипно-шатунном механизме.

Угол поворота коленчатого вала _ф = 375- (слева) и _ф = 420° (справа)

Гидродинамические силы и моменты в смазочном слое. При решении задачи нахождения гидродинамических реакций в смазочном слое приняты следующие допущения:

• 1)    давление по толщине смазочного слоя принято постоянным;

• 2)    давление на границах конечно-разностной сетки принимается картерным;

• 3)    вязкость смазочной жидкости принимается постоянной и не зависит от давления и координат точек слоя смазки;

• 4)    смазка рассматривается как ньютоновская жидкость, в которой напряжения пропорциональны скоростям деформации;

• 5)    течение смазочного слоя принято ламинарным;

• 6)    температура смазочного слоя принята по результатам экспериментальных исследований [4, 5].

Для получения гидродинамических сил и моментов, определялись функции распределения нормальных и касательных давлений в смазочном слое по всей боковой поверхности поршня. Исходным уравнением для определения этих давлений являлось уравнение Рейнольдса [6–9]. При этом решение уравнения Рейнольдса получено совместно с решением системы уравнений движения поршня и с учетом результатов расчета переменного НДС поршня. Таким образом, если не учитывать инерционные эффекты в смазочном слое и считать масло несжимаемым ( р = const), уравнение Рейнольдса может быть записано в следующем виде:

4 h3 *   hl дx ^ ц дx J dz ^ ц

d p д z

\

= ⁶

- 2 V

-

U * + W * dx    dz

после преобразований

3 h ² d h d P  h ³ d ² p  3 h ² d h d P  h ³ d ² p _f

+++ = 6 6

ц d x d x    ц d x ²    ц d z d z    ц d z ²

—

2 V —

U * ₊ w ^ h

d x

d z

где h – текущая толщина смазочного слоя; p – нормальное давление, возникающее в смазочном слое в рассматриваемой точке боковой поверхности; U , V , W – окружная, радиальная и осевая скорости поверхности поршня, ограничивающей смазочный слой; ц, р - динамическая вязкость и плотность смазочного материала.

Течение смазочного слоя в зазоре между поршнем и цилиндром порождает касательные усилия, преодоление которых требует затрат энергии. Суммарные касательные напряжения, эквива- лентные этим затратам определяются по зависимостям:

τ

x

h d p    U

= --+ ц —;

2 d x    h

τz

h d p   W

---+ ц — .

2 d z     h

Анализ вязкостно-температурной характеристики моторного масла показал, что в диапазоне температур рабочего режима вязкость масла в течение цикла изменяется не более чем на 6 %, и может быть принята как постоянная при расчете гидродинамических параметров в смазочном слое. Тепловое состояние масляного слоя в зазоре между поршнем и цилиндром было получено экспериментально [4, 5].

Поскольку профиль юбки поршня представляет собой сложную овально-бочкообразную поверхность, возможно только численное решение уравнения Рейнольдса с дискретизацией расчетного поля слоя смазки. Такая дискретизация была достигнута созданием конечно-разностной сетки на юбке поршня – разбиением боковой поверхности на двумерные прямоугольные регионы. Граничные условия для гидродинамических давлений задавались в виде постоянных величин картерного давления на границах юбки поршня.

Таким образом, решение данного дифференциального уравнения (краевой задачи) конечноразностным методом свелось к формированию и решению системы линейных алгебраических уравнений A ■ X = B , где A - матрица коэффициентов, X - вектор неизвестных гидродинамических давлений, B – вектор правой части уравнения.

Для решения этой системы был применен метод LU разложения матрицы A , основанный на том, что если главные миноры матрицы отличны от нуля, тогда матрицу A можно представить, причем единственным образом, в виде произведения A = LU, где L - нижняя треугольная матрица с ненулевыми диагональными элементами и U – верхняя треугольная матрица с единичной диагональю.

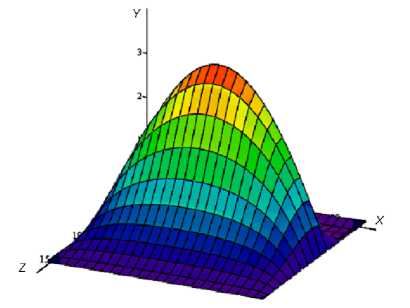
Результатом решения данной системы являются функции распределения нормальных и касательных давлений (рис. 6). Суммарная величина гидродинамической реакции была получена интегрированием элементарных составляющих сил по всем элементарным площадкам на боковой поверхности поршня.

Траектория движения поршня в цилиндре. Наибольшую информацию о параметрах на-груженности ЦПГ дает траектория движения поршня. Для заданных нагрузок решение системы уравнений движения одновременно с гидродинамической задачей позволяет рассчитать координаты центра поршневого пальца, а затем и критерии, характеризующие механические потери сопряжения.

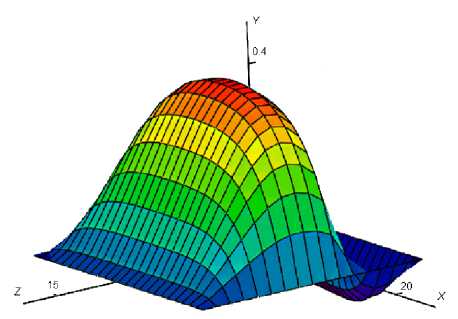
Рис. 6. Распределение нормальных давлений по боковой поверхности поршня, МПа, (слева и справа соответственно) при угле поворота коленчатого вала _ф = 420°

Однако описание поведения вязкой несжимаемой смазки в зазоре между поршнем и цилиндром уравнениями гидродинамики возможно только при условии ненулевых скоростей поршня. А поскольку поршень в цилиндре совершает возвратно-поступательные движения со знакопеременными скоростями и ускорениями, то при работе ЦПГ возникают участки, на которых скорость поршня близка к нулю. Такие участки, как правило, лежат в окрестностях верхней и нижней мертвых точек и характеризуются недостаточной несущей способностью смазочного слоя или граничным режимом трения в сопряжении. В рамках данной методики траектория поршня на этих участках определяется по результатам экспериментальных данных [5]. В дальнейшем планируется провести сравнительные расчеты по методике, описанной и примененной в работах [10, 11], которая позволяет рассчитывать динамику поршня на смазочном слое вблизи мертвых точек.

Одновременно с этим участки, где поршень движется со скоростями, при которых гидродинамические реакции от смазки достаточны для уравновешивания боковой силы и опрокидывающего момента, характеризуются жидкостным режимом трения. Величина гидродинамической реакции в этом случае является функцией от положения поршня в цилиндре (толщины смазочного слоя), т. е. справедлива система уравнений движения поршня: —          —             —

• m n z = R z + F z ( ф );

• m n^ R y + F y ( Ф );

——

J n g n = M o + M o ( ф );

• ф = ф ( t ),

где F_z (ф), F_y (ф), M_o (ф) - внешние силы и моменты, действующие на поршень в КШМ; R z , R y , M_o - реакции и момент, действующие на поршень со стороны смазочного слоя; ф - угол поворота коленчатого вала; t – текущее время.

Для решения этой системы уравнений был применен метод, основанный на так называемых формулах дифференцирования назад (ФДН). Этот метод предусматривает сведение системы дифференциальных уравнений второго порядка к системе первого порядка и использование обратного метода Эйлера. Обратный метод Эйлера – это пример неявного алгоритма интегрирования, в котором для определения функции на i + 1 шаге требуются дополнительные вычисления, так как неизвестные значения i + 1 входят как в левую, так и в правую части разностного уравнения. При этом неявные методы по сравнению с аналогичными прямыми алгоритмами более устойчивы и дают более высокую точность вычислений – это обусловлено наличием именно i + 1 члена в правой части разностного уравнения, что может рассматриваться как вид обратной связи.

Таким образом, результатом решения этой системы являются функции перемещения поршня в поперечном направлении цилиндра (вдоль оси OY ) и функции угла наклона поршня в цилиндре по времени. Эти зависимости в сравнении с экспериментальными данными на расчетном режиме представлены на рис. 7, 8.

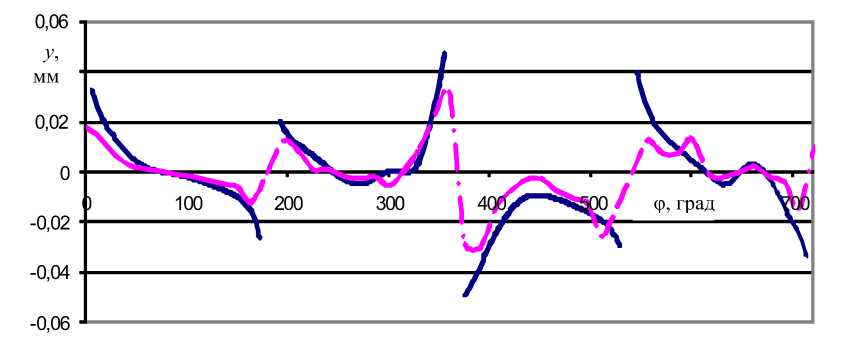
Рис. 7. Координаты центра пальцевого отверстия поршня y в зависимости от угла поворота коленчатого вала φ (сплошная кривая – расчет; штрихпунктирная – эксперимент)

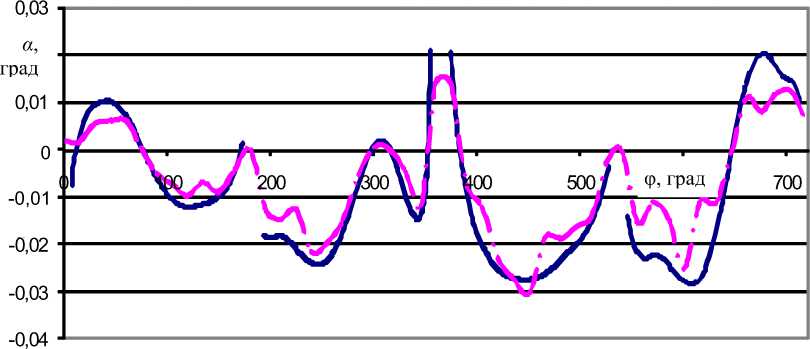
Рис. 8. Угол наклона поршня α в зависимости от угла поворота коленчатого вала φ (сплошная кривая – расчет; штрихпунктирная – эксперимент)

Анализ полученных результатов позволяет определить точки перекладки поршня и с учетом рассчитанного НДС выделить пятна контакта пары. Кроме этого, представляется возможным выявить участки с характерными режимами трения (жидкостным и граничным), а также оценить величину механических потерь в условиях жидкостного режима трения. Для двигателя ВАЗ21083 на расчетном режиме установлено, что поршень 4-го цилиндра работает в условиях граничного трения 12,63 % времени цикла.

Сравнение результатов расчетов по предложенной методике с экспериментальными данными показывает достаточную качественную сходимость. Осредненная погрешность расчетной методики при определении траектории составляет не более 21 %. Данная погрешность может быть связана со значительными допущениями, принятыми при расчете переменного НДС поршня, и погрешностями измерений при экспериментальных исследованиях.

Заключение. Предложенная методика описания динамики поршня позволяет установить функциональную связь между конструкцией ЦПГ и параметрами, характеризующими эффективность работы двигателя в целом. Расчетная часть методики представляет собой математическую модель, реализованную в виде прикладной программы разработанной в среде Turbo Pascal v. 7.0.

Дальнейшее направление исследований будет связано с практическим применением разработанных математических моделей и средств измерительной техники [4] для разработки методики оптимизации конструкции поршней ДВС.