Динамика причаливания и стыковки космического робота-манипулятора с геостационарным спутником

Современные геостационарные спутники связи (ГСС) имеют гарантированный срок активного существования до 17 лет. Для продления срока службы перспективных ГСС предусмотрено их обслуживание с помощью космических роботов-манипуляторов (КРМ), которые стыкуются с ГСС и обеспечивают стабилизацию формируемой конструкции в орбитальной системе координат (ОСК).

В системе управления движением (СУД) КРМ используются такие приводы: кластер гироди-нов (ГД) и электрореактивные двигательные установки (ЭДУ) на основе как плазменных, так и каталитических электрореактивных двигателей (ЭРД). Измерение координат движения КРМ выполняется бесплатформенной инерциальной навигационной системой (БИНС) с коррекцией

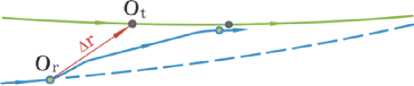
Рис. 1. Схема сближения КРМ с ГСС

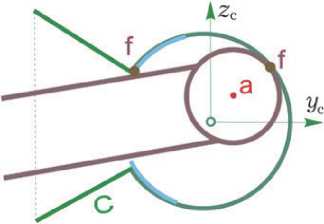
Рис. 2. Схема стыковки типа «штырь – конус»

сигналами от спутников GPS/ГЛОНАСС и звездных датчиков. При дальности до ГСС менее 100 м в СУД робота применяются также видеокамеры и лидары.

Вопросы выведения КРМ на геостационарную орбиту (ГСО) и его сближения с ГСС рассмотрены авторами [1-4], см. рис. 1 с траекториями перемещения центров масс спутника (цели, target) O _t и робота (robot) O _r в инерциальной системе координат (ИСК) O _⊕ X ⁱ Y ⁱ Z ⁱ . В данной статье исследуется динамика КРМ в процессе его швартовки (причаливания) и далее жёсткой фиксации к корпусу ГСС с применением стыковочного механизма (СМ) класса «штырь – конус».

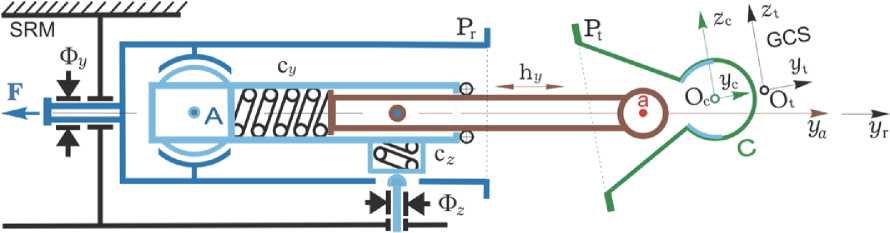
Рис. 3. Схема перемещения активного агрегата при швартовке КРМ к ГСС

ОПИСАНИЕ ЗАДАЧИ

Основы теории и техники стыковки космических аппаратов (КА) представлены в известной монографии В.С. Сыромятникова [5]. В рассматриваемом классе конструкций стыковки КА выделяются активный агрегат, содержащий штырь, и пассивный агрегат в виде приёмного конуса, рис. 2. На одном конце штыря (коричневый цвет) закреплена сферическая головка увеличенного диаметра с центром в точке a (красный цвет), см. рис. 2. Штырь со сферической головкой входит в состав СМ активного агрегата, рис. 3. Здесь другой конец штыря упруго закреплен во внутренней обойме (голубой цвет) активного агрегата, которая допускает как линейное перемещение штыря вдоль продольной оси y_a , так и его угловое перемещение вокруг поперечных осей x_a и z_a относительно точки A, см. рис. 3. При этом внешняя обойма (тёмно-синий цвет) активного агрегата с плоским стыковочным кольцом P _r может перемещаться вдоль продольной оси y _r космического робота-манипулятора (space robot-manipulator, SRM), см. рис. 3. Пассивный агрегат в виде приёмного конуса C (cone, зелёный цвет) с гнездом и плоским стыковочным кольцом P _t жёстко закреплен на корпусе геостационарного спутника связи (geostationary communications satellite, GCS), см. рис. 3.

Конструкции СМ класса «штырь – конус» для перспективных КА представлены в [6,7], а математические модели взаимодействия активного и пассивного агрегатов при стыковке двух КА – в статьях [8,9,10]. Стыковка КРМ с ГСС содержит три последовательно выполняемых этапа, именно 1) причаливание, 2) стягивание, 3) выравнивание и фиксация, которые кратко описываются ниже.

• 1.    При швартовке ( причаливании ) КРМ к ГСС головка штыря после нескольких соударений с поверхностью приёмного конуса C проникает внутрь гнезда через его горловину с электромеханическим затвором, который отмечен голубым цветом как на рис. 2, так и на рис. 3. При этом событии затвор срабатывает и уменьшает проходной диаметр горловины гнезда до диаметра поперечного сечения штыря. В результа-

• те между штырем и внутренней поверхностью гнезда вместе с затвором возникает первичная механическая связь, в общем случае в двух точках f, см. рис. 2. Далее происходит поглощение кинетической энергии пространственного относительного движения двух КА в стыковочном механизме за счёт его упругодемпфирующих механических связей при линейных деформациях h i , i = x, y, z, пружин с коэффициентами жёсткости ci и обобщенных сил как вязкого, так и сухого трения, реализуемых фрикционами Φ i, см. обозначения на рис. 3. После затухания скоростей всех координат СМ до приемлемого уровня причаливание завершается и формируется сцепка агрегатов с малыми изменениями их линейных и угловых рассогласований.

• 2.    Стягивание агрегатов вдоль продольной оси y _r КРМ реализуется электромеханическим приводом класса «винт – гайка» с вектором силы F для внешней обоймы активного агрегата, рис. 3.

• 3.    Выравнивание стыковочных колец P _r активного и P _t пассивного агрегатов и фиксация их взаимного положения выполняется электромеханическими приводами стыковочного механизма.

На рисунке 4 приведена упрощенная схема результирующей жёсткой механической связки КРМ и ГСС после завершения их стыковки. Здесь не представлены панели солнечных батарей (СБ) КРМ и ГСС, бортовой манипулятор антропоморфной структуры с 4 звеньями и 6 степенями свободы [11] находится в походном состоянии и размеры всех элементов конструкции, включая топливные баки электрореактивной двигательной установки (ЭДУ), указаны в метрах.

При описании движения КРМ и ГСС в рассматриваемом режиме применяются (i) экватори-аль-ная инерциальная система координат (ИСК) I _⊕ с началом в центре Земли O _⊕ , (ii) связанная система координат (ССК) B (O xyz ) с началом в полюсе O , которая совпадает с системой координат O _r x _r y _r z _r КРМ, (iii) орбитальная система координат (ОСК) O (O x ^o y ^o z ^o) с началом в полюсе O и ортами r ^o , τ ^o , n ^o , которая имеет следующие направления осей и ортов: ось O x ^o направлена по радиали r ^o , ось O z ^o – по нормали

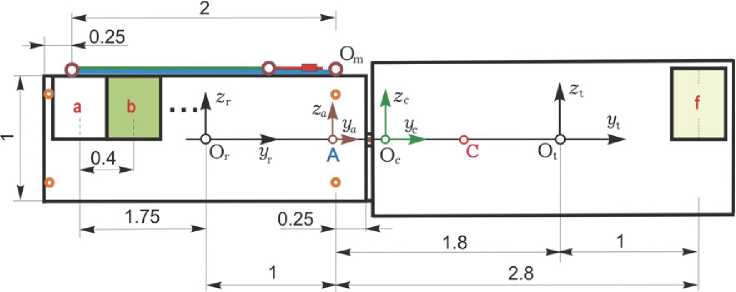
Рис. 4. Схема результирующего соединения космического робота с геостационарным спутником

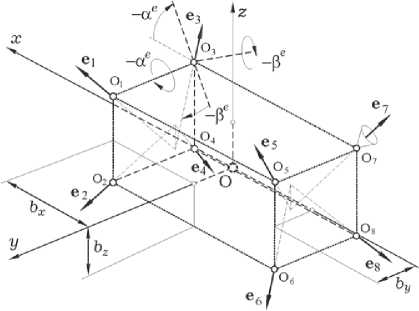
Рис. 5. Схема ЭДУ с 8 каталитическими ЭРД

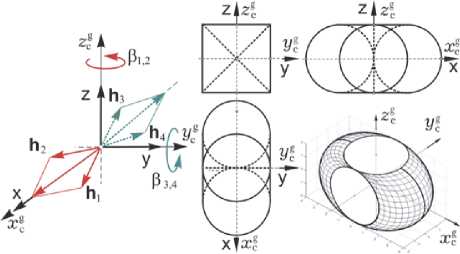
Рис. 6. Схема СГК и область вариации его КМ

n o к плоскости орбиты, а ось O у ⁰ - по трансверсали т ⁰ и направлена в сторону орбитального движения КРМ; система координат O _t x _t у _t z _t , связанная с ГСС (цель, target) в центре масс O _t спутника; система координат A x ayaza , связанная со штырём активного агрегата, и система координат O _c x _c у _c z _c приёмного конуса C пассивного агрегата, см. рис 4. Используются также обозначения col( - ) = { • } , line( - ) = [ • ] , ( - , - ) , [ x- ], ( • ) , [ a x ] и ° ,~ для векторов, матриц и кватернионов, а также матриц [ a ] i стандартного элементарного поворота вокруг i -ой оси на угол α при i = 1,2,3 = 1 ^ 3 .

В данном режиме приводами СУД робота-манипулятора являются ЭДУ с 8 каталитическими электрореактивными двигателями (ЭРД) (рис. 5) при широтно-импульсной модуляции (ШИМ) их тяги и силовой гироскопический кластер (СГК) на основе четырех гиродинов (ГД) по схеме 2-SPE с ортами векторов кинетических моментов (КМ) h p ( в p ) , p = 1 ^ 4 , рис. 6, где приведена также область вариации нормированного вектора КМ h ( P ) = S h p ( в p ) кластера со столбцом в = {Р p } и ее проекции на плоскости гироскопического базиса O x g у g z g .

Применяемый явный закон настройки СГК (распределения вектора его управляющего момента M ^g = {М^g} между ГД) позволяет исключить избыточность кластера с вектором КМ

H = h h ( P ) , где h_g - одинаковое для всех четырех ГД постоянное значение модуля его собственного КМ.

Ориентация ССК B в ИСК I _@ определяется кватернионом Л = ( X ₀ , X ) , где X = { X i } , вектором модифицированных параметров Родрига (МПР) о = { с i } = е ^e tan( Ф /4) с ортом e ^e оси Эйлера и углом Φ собственного поворота. В ИСК I _@ кинематические уравнения для вектора r _r расположения КРМ, кватерниона Л и вектора МПР σ имеют вид

rr = tr‘+®xrr;    Л=Л ° й 2о =1 (1 - о2)® +1 о x й +1 (о,®)о.

где вектор ω представляет угловую скорость корпуса КРМ и используется обозначение ( • ) ‘ локальной производной по времени.

Ориентация базиса O в базисе I _@ определяется углами рыскания ф 1 = у , крена ф ₂ = ф и тангажа ф ₃ =0 в последовательности 132, кватернионом Л ^o и матрицей C o = [ ф ₂ ] ₂ [ ф ₃ ] ₃ [ ф 1 ] 1 направляющих косинусов координатного перехода от ОСК к ССК.

Погрешность ориентации базиса B в орбитальном базисе O определяется кватернионом E = Л ^o ° Л- ( e ₀ , е ) , где e ₀ = соз( Ф ^е /2 ), е = sin ( Ф ^e / 2 ) е ^e с ортом е ^e оси Эйлера и

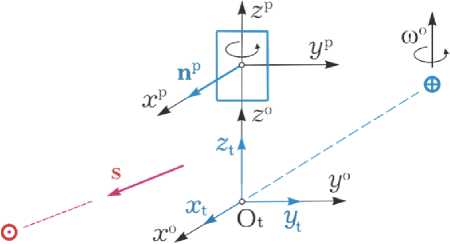
Рис. 7. Штатная ориентация ГСС в ОСК углом Фе, матрицей Се = I3 — 2[ex]Q‘, где Qе = 13e0 + [ex], вектором угловой погрешности 8ф = {8фi} = {2e0ei} и вектором МПР СТе = {сте} = ee tan(фе / 4). При этом вектор погрешности по угловой скорости вычисляется в виде 8® = ® — Се®°(t), где вектор ®°(t) представляет скорость вращения базиса O в базисе I @ .

Если считать КРМ твёрдым телом с массой mr и тензором инерции J r, то модель динамики его пространственного перемещения в проекции на оси ССК Or xyz имеет вид mr (v'r + ®x v ) = Pе + Fd;

(2) J _r ® + ® x G = M ^g + M ^е + T ^d.

Здесь G = J ω+ H является вектором КМ робота, векторы P ^е , М ^е и M ^g =— H ' представляют соответственно управляющие силы РДУ, моменты РДУ и СГК, а векторы F ^d и T ^d -внешние возмущающие силы и моменты. Применяемые в СУД робота дискретные алгоритмы широтно-импульсного управления ЭДУ и цифрового управления СГК детально представлены в [12].

На рисунке 7 представлена штатная ориен- тация системы координат Otxtytzt ГСС в ОСК. Здесь орт s нормали к рабочей плоскости панелей СБ регулярно наводится на Солнце, а электрические оси его приёмно-передающих антенн ориентируются на Землю – в надир.

При исследовании динамики причаливания и стыковки КРМ с ГСС анализировались вариации разностей векторов скоростей их поступательного A v = { A v i } и углового A ® = { A® i } движений, а также изменения вектора А ф = { Аф i } взаимной угловой ошибки.

Автоматические режимы причаливания и стыковки как грузовых, так и пилотируемых космических кораблей с международной космической станцией (МКС) на низкой орбите давно и успешно применяются в отечественной космонавтике. Здесь отношение массы КРМ m _r к массе МКС (цели) m _t составляет = 1/30 = 0.033. В данной работе исследования выполнялись при значениях m _r = 3100 кг и m _t = 3500 кг, т.е. для отношения масс 3.1/3.5 » 0.89 (в 27 раз большем) для КА на геостационарной орбите. Основная цель статьи заключаются в анализе динамики автоматического причаливания и стыковки КРМ с ГСС при их сопоставимых инерционных характеристиках по массе и тензору инерции, включая приведение сформированной жесткой связки этих двух КА в орбитальную систему координат с последующей угловой стабилизацией.

РЕЗУЛЬТАТЫ ИМИТАЦИИ ДИНАМИКИ СТЫКОВКИ

Исследование выполнено при значениях параметров систем управления космического робота и ГСС, представленных в статьях авторов [13,14]. В таблице 1 приведена информация об

Таблица 1. Этапы причаливания и стыковки космического робота с геостационарным спутником связи

№ п/п	Служебные операции этапа	Полуинтервал времени t	Управление СГК КРМ	Управление ЭДУ КРМ
1	Наведение штыря на приёмный конус, терминальное управление	t е [0,137), 5	Наведение и управление ориентацией	Управление с ШИМ тяги
2	Ударные перемещения штыря в конусе до захода его головки в гнездо	t е [137,141.8), 5	Стабилизация и компенсация возмущения	Разгрузка СГК с ШИМ тяги
3	Перемещения головки в гнезде, поглощение энергии, причаливание	t е [141.8,161.7), 5	Стабилизация и компенсация возмущения	Разгрузка СГК с ШИМ тяги
4	Стягивание до уровня 10 мм между стыковочными плоскостями	t е [161.7,211), 5	Стабилизация и компенсация возмущения	Разгрузка СГК с ШИМ тяги
5	Угловое выравнивание стыковочных плоскостей, завершение стыковки	t е [211,261), 5	Стабилизация и компенсация возмущения	Разгрузка СГК с ШИМ тяги

этапах причаливания и стыковки КРМ с ГСС. Рисунок 8 представляет траекторию перемещения центра головки штыря (точка a, красный цвет, см. рис. 2.) при швартовке КРМ к ГСС. Здесь 3-D отображение траектории показано на рис. 8 а , а проекция этой траектории на плоскость x _c O _c y _c системы координат приёмного конуса – на рис. 8 b.

Изменение координат взаимного перемещения КРМ и ГСС, а также деформации пружин активного агрегата в процессе причаливания КРМ к ГСС приведены на рис. 9 и 10 соответственно. Здесь исследованы потенциальные возможности увеличения вязкого демпфирования координат активного агрегата при использовании реологических суспензий, управляемых магнитным полем.

Рисунки 11, 12 и 13 представляют динамические процессы приведения сформированной жесткой связки этих двух КА в ОСК с последующей угловой стабилизацией.

ЗАКЛЮЧЕНИЕ

Рассмотрены задачи управления космическим роботом-манипулятором в процессе его причаливания и стыковки с геостационарным спутником связи при использовании стыковочного механизма класса «штырь – конус». Выполнен анализ динамики при вариации терминальных условий причаливания и кратко представлены результаты компьютерной имитации.

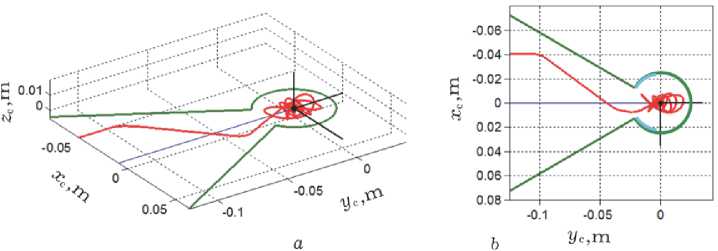
Рис. 8 . Траектория перемещения центра головки штыря при швартовке КРМ к ГСС

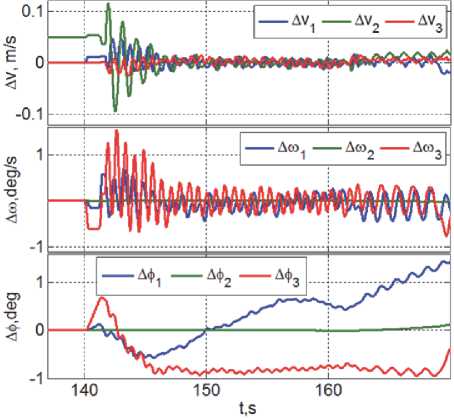
Рис. 9. Изменение координат взаимного движения КРМ и ГСС при швартовке

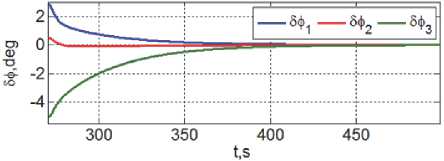
Рис. 11. Ошибки ориентации после стыковки

140           150           160

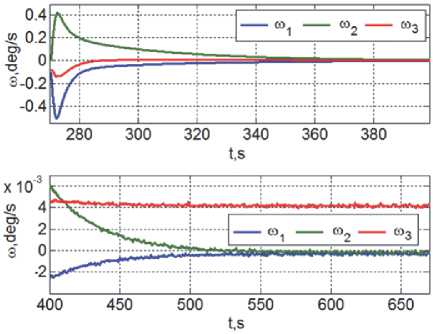
Рис. 12. Угловая скорость после стыковки

t,S

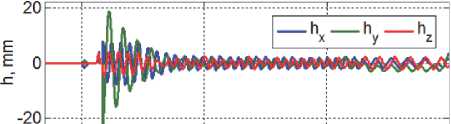
Рис. 10. Деформации пружин активного агрегата в процессе причаливания КРМ к ГСС

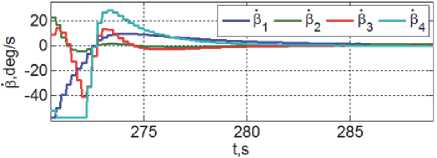
Рис. 13. Цифровые команды управления СГК