Динамика пыли вблизи тяготеющего центра. Интегралы движения

Общая проблема образования дисковых структур вблизи компактных гравитирующих объектов, а также проблема аккреции вещества на них, является одной из центральных проблем современной астрофизики [1 –3] , особенно в области релятивистских объектов [1, 4 –7] . Но и в случае нерелятивистских объектов, таких как галактики [10] , планетарные структуры у маломассивных звезд или дисковые структуры вокруг планет гигантов, задачи такого рода также имеют важное значение. В силу этого даже упрощенные модели дисковых структур [10] , но допускающие детальный математический анализ, представляют интерес, хотя на них часто не обращают должного внимания. Например, в работах по аккреции или звездной динамике в галактиках практически отсутствуют работы, которые бы описывали исчерпывающим образом классические по сути результаты в этой области. В частности, в книге [10] приводятся простые модели движения звезд в Галактике, которые исследовал Линдблад [10] , однако в рамках классического подхода можно получить гораздо более обширный класс моделей, который может дать полезную информацию и для задач более сложных. Это обусловлено тем, что большинство сложных моделей, включающих множество различных факторов, нельзя исследовать точными методами. Для их теоретического анализа прибегают к приближенным вычислениям с помощью теории возмущений в разных ее вариантах. Однако нулевой порядок таких приближенных теорий как раз и опирается на упрощенные классические модели, для которых можно построить точные решения. В силу этого классические задачи требуют более глубокого внимания, чем это имеет место в настоящее время.

В данной работе предлагается достаточно подробный анализ классической задачи о динамике пыли в поле тяготеющего центра, результатом которого является описание общих интегралов движения, необходимых для построения решений различного уровня, в том числе неосесимметричных и нестационарных. Как показывает анализ литературы, полный набор интегралов движения в подходяшей форме для этой классической задачи не публиковался. В качестве примера анализируются простые примеры построения решений, которые могут служить прообразом более сложных явлений, встречающихся в реальных ситуациях, где задача динамики в поле тяготеющего центра играет важную роль.

При решении задачи в опреленной степени используется упрощенный вариант метода гидродинамических подстановок, развитого в работах [11–14]. В данной работе он используется в упрощенном виде, поскольку задача решается в предположении малости собственного поля тяготения самой пыли. Фактически идеология общего метода гидродинамических подстановок используется только для описания распределения плотности пыли. В рамках рассматриваемой задачи решение для плотности пыли при отсутствии самогравитации строится отдельно от решения задачи об эволюции скорости потока.

2.    Уравнения течения пыли в поле тяготеющего центра

Уравнения динамики пыли в поле тяготения компактного тела во вращающейся системе отсчета в случае, если собственным полем тяготения пыли можно пренебречь, можно записать в следующем виде:

ut + ( u , V ) u = - 2Q[ n x u ] - px ,                          (1)

^|x| 3

p t + div( u p) = Q.                                                  (2)

Здесь u ( x ,t) — поле скорости среды, как функции координат x = (х 1 ,х ² ,х ³ ) = (х, у, z) и времени t. Состояние среды описывается ее плотностью массы p(x, t) при равном нулю давлении. В качестве объемных сил, действующих на пыль в данной модели учитывается лишь сила Кориолиса для вращающейся с постоянной угловой скоростью П вдоль оси z ( n = (Q, Q, 1)) и поле тяготения центрального тела с массой М : р = MG, где G — постоянная тяготения. Уравнение ( 1) предполагает, что гравитационным полем самой пыли можно пренебречь по сравнению с полем тяготеющего тела. Основной задачей дальнейшего исследования будет отыскание интегралов движения среды, применяя на первом этапе упрощенный вариант метода гидродинамических подстановок. На основе полученных выражений для интегралов движения будет рассмотрено частное решение динамики пыли вблизи плоскости диска.

3.    Гидродинамические подстановки в трехмерном случае

Для построения решения уравнений ( 1 ) воспользуемся вариантом метода гидродинамических подстановок, приспособленным к многомерным задачам, основные идеи которого были изложены в работе [12] . В соответствии с общей идеей работы [12] , c каждой точкой среды можно формально связать набор маркерных функций е ^а = e ^a ( x , t), а = 1,2, 3, значения которой привязаны к этим точкам. Это означает, что уравнение переноса маркеров можно записать в следующем виде:

а „ д „ _{z z} ,        „

Lе = — е + (u(х,t), V)e = Q, а = 1, 2, 3, где введено обозначение:

д /          \

^L = $ + (uM^V)

для оператора переноса потоком с полем скорости u(x, t). Как и в одномерном случае [13,14], дифференциальным следствием этого соотношения является дифференциальный закон сохранения (2), в котором полагается:

дх “ / де ^а

д де ^а дt дх ^а

ди ^ де     о д де

+     + U дх“ дх^     дх^ дха

= Q.

Здесь использованы известные тождества:

дх“ д деа   д lndet G  дх“ д деа   д lndet G деа дt дха дt ,  деа дх^ дха дх^

Заметим, что в исходной системе уравнение для плотности среды может решаться отдельно от уравнения для скорости потока. Это позволяет решать задачу в два этапа. Сначала строятся решения для u , а затем уже для эволюции плотности.

Возможность получить в качестве тождества уравнение сохранения массы, используя только формальное уравнение переноса маркеров ( 3 ), дает эффективный метод построения точно решаемых моделей течения жидкости в собственном поле тяготения для задач с плоской, цилиндрической и сферической симметриями [13, 14] . Для трехмерных течений вариант гидродинамических подстановок в общих чертах был развит в [12] . Здесь мы его применим в упрощенном виде.

4.    Подстановка для скорости потока

Рассмотрим гидродинамическую подстановку следующего вида:

u = a( x , t)[ n x x ] + b(x, t)x + c( x , t)n,

где n — единичный постоянный вектор, направленный вдоль оси -: n = (0, 0,1). Функции a, b, c характеризуют компоненты гидродинамического потока в системе: тороидальный — a(x, t), радиальный — b(x, t) и вдоль оси - — c(x, t).

Действуя на это векторное поле оператором L , находим:

Lu = [ n x x

] (Lа)

+ a[ n x u ] + x

(Lb)

+ u b( x , t) + n

( L c).

Левая часть этого уравнения совпадает с эйлеровым ускорением среды. Приведем правую часть этого соотношения к виду ( 1 ). Для этого сделаем простые преобразования и для части слагаемых в правой части ( 7 ) заменим компоненты поля скорости на их значения из ( 6 ). Имеем:

Lu = [ n x x

] (L a) - 2Q[ n

x u ] + n

(^{L c}

+

+(a + 2^) (a[ n x [ n x x ]] + b[ n x x ] ) + x ( L b ) + b( x , t) (a[ n x x ] + b x + c n) .

Раскрывая двойное векторное произведение:

[n x [n x x]] = nz — x, и собирая все слагаемые при векторах тороидальной, радиальной и нормальной компонент, приходим к следующему соотношению:

Lu = — 2fi[ n x u ] + x^L b + b ² — (a + 2fi)a) +

+ [ n x x ] ^L a + 2(a + fi)b) + n^L c + cb + (a + 2fi)az^ .

Для того, чтобы данное уравнение имело вид уравнения ( 1 ), достаточно выполнения трех уравнений для функций a, b, c:

L a + 2(a + fi)b = 0,

L b + b ² — (a + 2fi)a = — ^, ^|x| 3

L c + cb + (a + 2fi)az = 0.

Эти уравнения представляют собой замкнутую систему относительно амплитуд компонент течения, которую мы и будем в дальнейшем анализировать.

5.    Свойства оператора переноса

Прежде, чем решать систему уравнений ( 8 ), рассмотрим общие свойства оператора переноса L , соответствующие потоку ( 6 ). В соответствии с определениями ( 4 ) и ( 6 ), имеем:

d /          \                d

L = yt + a(^[ n x x ], Vj + b( x , V ) + c^-.

Поскольку:

n x x ], v) = [x

5y

5 \     5

У дх) дф’

где ф — азимутальный угол в плоскости х, у, оператор L можно записать в виде:

д д д    д

L = 5t+ “аф +   ■ ■ + (zb + с) 55’ где т = ^т2 + у2 — радиальная координата в плоскости х,у. В результате, система (8) представляет собой неоднородную систему трех квазилинейных уравнений, решение которой можно искать с помощью метода характеристик.

6.    Метод характеристик

В общем случае метод характеристик в применении к системе уравнений ( 8 ) сводится к решению системы обыкновенных дифференциальных уравнений вдоль характеристик:

dф d ln т , dz

л = “’ Х7Т = ^b’ at =^{(Л + с )} ’

— = — 2( й + O)b, — = — b ² + ( й + 2П) й — А, т = —сЪ — ( й + 2П)аа. dt                      dt                             | x | 3 dt

Подставляя выражения для b из системы ( 10 ) в первое и второе уравнение системы ( 11 ), приходим к следующим уравнениям:

d ln(a + П) dt

_ d ln т

² IT’

d2 ln т     d In т 2                      M dt2 +(IT ) = (й +   )a — (z2 + т2)3/2 ■

Первое уравнение интегрируется, что дает первый интеграл 1 1 движения системы вдоль характеристики:

1 1 = ( й + П)т ² = const.

Интеграл движения 1 1 представляет собой момент импульса точек среды. Второе уравнение в ( 12 ) в результате приводится к следующему виду:

d^ =   _ о2г _ мт dt2     т3             (z2 + т2)3/2.

Для получения уравнения изменения z вдоль характеристик удобно ввести вместо с новую функцию ^( x , t), полагая: с = z^( x , t). В этом случае уравнения для с примут вид:

^ln^ = b + h, ^^ + h^^ = — hb — (а + 2П) й. dt            dt dz

Второе уравнение можно теперь записать в следующем виде:

— + h ² + 2bh = — ( й + 2П)а.

Складывая это уравнение с уравнением для b системы ( 11 ), приходим к уравнению:

^{d ( h} +^b) +(b + h) ² = —

М

(z ² + т ² ) ³ / ² .

В результате приходим к уравнению для z в следующем виде:

d ² z dt ²

Mz

(z ² + т ² ) ³ / ² .

Таким образом, система для вычисления характеристик может быть записана в следующем виде:

ф = — п+ Г 2 ,

^Г = ^ - ^^Г - ,, 2 /^ ^ 2 . 3 2 ’                                  ⁽¹⁷⁾

мг z = - (^2+72)3/2 ■

Эти уравнения представляют собой в точности уравнения Ньютона кеплеровского движения в поле тяготеющего центра в системе отсчета, вращающейся в плоскости ж, у с угловой скоростью П, с тем отличием, что они описывают отдельные характеристики гидродинамического потока, а не одну частицу. По сути, каждая отдельная характеристика описывает движение бесконечного множества частиц, имеющих одинаковые интегралы движения, но положение которых на характеристике определяется начальными условиями. Поскольку исходные гидродинамические уравнения не содержат никаких диссипативных сил или сил, ответственных за столкновение отдельных частиц пыли, то пересечение характеристик друг с другом не будет влечь за собой изменений в движении частиц. Но с гидродинамической точки зрения, области пересечения характеристик будут соответствовать области “ перемешивания ” гидродинамического потока, что можно, в принципе, трактовать как возникновение области турбулентности, хотя для описания последней требуются иные методы математического анализа. Поэтому с гидродинамической точки зрения решения ( 17 ) интерпретируются иначе, чем при движении только одной частицы. Хотя для всех типов характеристик, удовлетворяющих уравнениям ( 17 ), известны точные формулы, соответствующие всем возможным кеплеровским траекториям, тем не менее их конкретная совокупность для каждого гидродинамического потока требует определения из начальных и граничных условий. Отыскание таких комбинаций траекторий и является дальнейшей задачей данной работы.

7.    Интегралы движения

Стандартным способом вычисления поля скорости потока, в рамках теории квазилинейных уравнений [15], является процедура вычисления всех их интегралов движения, если это возможно. Системы (10) и (17) (последняя вместе с 11) имеют шесть интегралов движения: Ij, к = 1, ■ ■ ■, 6, которые сов- падают с постоянными интегрирования уравнений. Для полного описания гидродинамического потока необходимо отыскать все шесть интегралов движения. Два последних уравнения в (17) представляют собой уравнения Ньютона:

д ,    ,            9, х r = — дт^(r,z), Z = — 92U(r,Z), для частицы в потенциальном поле с потенциальной энергией:

U(r,z) = ^ (12 +fi2r2) - М(18)

2 \r ²          )    ( z ² + r ² ) ¹ ! ²

Отсюда находим интеграл энергии I ₂ в следующей форме:

I2 = - ((Г)2 + (z)2^ + U(r, z) = - ^r2b2 + z2(b + к)2) + U(r, z) = const.

Два интеграла движения можно получить прямым интегрированием уравнений для функций а и к, если уже вычислена зависимость r и z от t вдоль траектории. Первый из них такой:

t

13= ф -1. / !₂-

Четвертый интеграл движения получается с помощью комбинации двух последних уравнений в ( 17 ).

Умножая первое из них на z, а второе — на r, приходим к следующим соотношениям:

zT — rz =

d                 Г ²

zr — rz = rz — П ■ dt                    r4

где 1 3 — интеграл движения, фактически эквивалентный интегралу ( 20) . Интеграл А выражается через интегралы I 1 и 12;

^А =\/² (^{I 2 +} I 2 ⁾ ■

Подставляя выражение для q, приходим к следующему выражению, связывающему г и ф ;

—    ,' I ^{А ( I} 1 ^{, I} 2 ⁾ СО8 ^{( ф} - I3) ,

Г     I 1

Используя это соотношение, из которого можно вычислить интеграл I 3 , проинтегрируем уравнение для ф. Имеем;

Ф 4 = _Г(7 + А cos(Ф)) ² , Г ²    I

где введены обозначения; Ф = ф — I 3 и 7 = —/Д. Интегрируя это соотношение, находим;

^{t — t} 0 = ^I 1 [ (₇ 2 А2 ) 3/2 arctg (^{Л tg} ( ^{Ф / 2} )) - 7 2 ^

! sin

А ² 7 + А.

(Ф) cos(Ф) '

Используя уравнения ( 10 ), приходим к следующему уравнению:

d                d              II zt — tz = — Tzn = tz — П .

dt                 dt                 t⁴

Отсюда находим еще один интеграл движения:

t

I 4 = Tzh + J tz    — П²^ dt.

Еще два интеграла движения должны получаться из решения последней пары уравнений ( 17 ), однако мы не будем находить в явном виде, ограничившись далее рассмотрением движения в плоскости z = 0.

Если все интегралы найдены, то три любые независимые функции от них:

Н р = Н _р (1 1 ,...,1б) =0, р = 1, 2, 3

дают полное решение задачи в том смысле, что функции а, Ь, с вычисляются из соотношений ( 22) .

8. Течения вблизи экватора

Рассмотрим приближенные варианты полученных решений, которые играют важную роль в астрофизических задачах. Это движение в плоскости тонкого диска, возникающего вокруг тяготеющего центра. Для такой задачи для построения решения достаточно использовать в явном виде только часть интегралов движения. Задача описания динамики системы вблизи экватора сводится к предположению z ~ еф , где е <<  1 — безразмерный малый параметр. В этом случае уравнение для т в ( 17 ) в нулевом порядке упрощается и принимают следующий вид:

••    l2      2 M т = “з — П т--2.

Уравнение для С относится уже к первому порядку теории возмущений:

Ё ₌ _^

ф        тз.

Нашей задачей будет построение решений для компонент радиальной и угловой скорости в плоскости экватора в нулевом порядке теории возмущений. Сделаем еще одно упрощение. Будем рассматривать динамику в невращающейся системе отсчета, то есть будем полагать П = 0, что в рассматриваемой постановке задачи не является существенным требованием.

Теперь в нулевом порядке уравнение для т может быть проинтегрировано, поскольку представляет собой уравнение радиального движения в задаче двух тел. Переход к соответствующему представлению интеграла энергии производится при отбрасывании слагаемого, пропорционального z ² , в результате чего интеграл энергии примет такой вид:

1 2,2 I2

I2 =   b + —

2 t2

Из этого соотношения можно однозначно вычислить функцию Ь. После замены Ь на производную из ( 10 ), уравнение энергии интегрируется с помощью перехода к производной по углу. Для этого необходимо переменную t вдоль характеристики заменить на переменную ф, пользуясь интегралом I 1 ( 13 ), и сделать

замену q = 1 1 т

1 . В этом случае интеграл энергии I 3 принимает вид:

Это соотношение позволяет вычислить интеграл I ₅ = t ₀ .

Таким образом, имеем следующие выражения для интегралов движения:

I 1 (a, г) = аг ² , I ₂ (a, b, г) = ^г2 Ь 2 + а ² г ² — ^— ,

ДА, А) = У² ^^I 2 ⁽ й ^{,ь,г ) +} й^ ) , 7 ^{( й} , ^{г )} = — ^й

1 г 2 ,

I ₃ (a, Ь,г,ф) = ф — arccos

а ² г ³ — —

аг ² А^аг ² , I ₂ (a, b, г))

,

^I 5 ⁽a^,b,г^,ф,t) = t

^ [ ₍₇ 2 —2 А 2 ) 3/2 ^arctg (^{Л tg} ( ^{Ф / 2} )) -

А ²

7 2 ^— -

sin(Ф)

А ² 7 + А cos(Ф)]

Интегралы I 3 и I 5 отвечают за зависимость функций от угловой переменной ф и от времени t. Четыре интеграла движения движения I 1 , I ₂ , I ₃ , I 5 , представленные в явном виде, полностью определяют движение в плоскости экватора. Два интеграла движения по оси z можно получить в первом порядке теории возмущений из решений уравнения ( 24 ).

9.    Статическое осесимметрическое распределение поля скорости

Как уже отмечалось, для вычисления функций й(г, ф, t) и Ь(г, ф, t) в нулевом порядке необходимо задать две произвольные функции от интегралов I 1 , I ₂ , I ₃ , I 5 ;

H 1 (I 1 ,I 2 ,I 3 ,I 5 ) =0, Я 2 (- 1 ,- 2 ,- 3 ,- 5 )=0■

Функциональный вид H 1 и Н ₂ , как функций от интегралов, должен вычисляться из начальных и граничных условий. Анализ всех таких условий в общем виде в силу сложности полученных решений требует отдельной работы. В данной работе мы приведем лишь простейший случай статического радиального распределения вблизи плоскости экватора.

При условии, что компоненты скорости не зависят от t и ф, уравнения ( 35 ) примут такой вид;

H 1 (- 1 ,- 2 )=0, H 2 (I 1 ,I 2 )=0.

Поскольку решением этих уравнений являются при любых Н 1 и Н ₂ постоянные значения для I 1 и I ₂ для всех характеристик одновременно, то решения для а и b имеют такой вид;

^й = 1 , , ^b = ±~V^I 2 ^— г^           г V

I + ^— •

где 1 1 и 1 2 постоянные, вычисляемые из граничных условий. Соответствующие линии тока находятся из ( 28 ), в предположении, что 1 1 и 1 2 для всех линий тока одинаковы, но каждая отдельная линия тока определяется значением интеграла ф ₀ = 1 3;

Р

Т = ---------ПЛ----~^.

1 + е cos(ф — ф ₀ )

Это соотношение является каноническим уравнением эллипса с фокальным параметром р = 1 1 / р и эксцентриситетом е = V2 V 1 2 Р 2 Щ + 1. В теории звездных систем [10] подобные траектории отдельных звезд называются эпициклическими орбитами Линдблада [10] . Однако от эпициклических орбит Линдблада данное решение дает описание гидродинамического потока, характеристики которого представляют собой множество эллипсов с фиксированными значениями эксцентриситета и фокального параметра, которые целиком определяются значениями интегралов 1 1 и 1 2 , одинаковыми для всех характеристик. Отличаются характеристики только третьим интегралом, что приводит к совокупности линий тока, занимающих кольцевую область, которые изображены на рисунке ( Рис. 1 ). Масштаб на рисунке выбран таким образом, что р = GM = 1, а так же 1 1 = 1, 1 2 = 0.995 для (1) и 1 1 = 1, 1 2 = 0.995 (2).

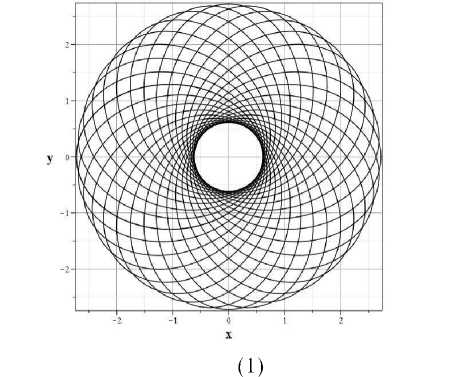
Рис. 1. Линии тока пыли значений 1 1 = 1 и; 1 - 1 2 = 0 . 8 , 2 - 1 2 = 0 . 995

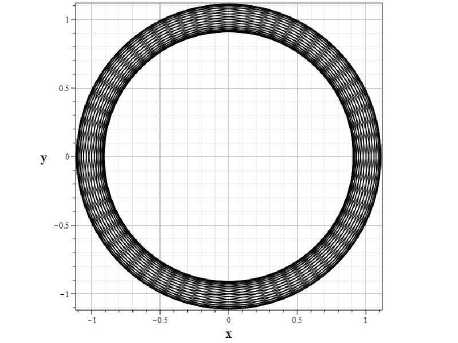
Полученные решения демонстрируют классический вариант кольцевых структур в дисках. Ширина кольца определяется эксцентриситетом е орбит, а внешний радиус — фокальным параметром. График (1) на рисунке (Рис. 1) в выбранных единицах длины соответствует значению эксцентриситета е = 0.632 (для 12 = —0.8), а графики (2) на этом же рисунке соответствуют значениям е = 0.1 (для 12 = —0.995). Чем уже кольцо, тем при меньших углах наклона пересекаются линии тока (характеристики) между собой. Следовательно, для узких колец возможные в реальности столкновения будут иметь незначительные последствия, поскольку относительные скорости частиц на разных траекториях малы. Кроме того, если теперь посмотреть на уравнение (24), то видно, что для узких колец; т ~ const, и уравнение для £ превращается в уравнение гармонического осциллятора с частотой, равной кеплеровской орбитальной частоте круговой орбиты. Это означает, что все характеристики в кольце могут лежать в слегка наклоненных к экватору z = 0 плоскостях. При этом толщина кольца на внешней границе будет больше, чем на внутренней. Нулевая толщина (в реальности – минимальная) будет соответствовать радиусу, равному расстоянию от центра до фокуса. На самом деле, этот вывод не зависит от выбранного нами приближения, соответствующего плоскости z ~ 0. Как уже отмечалось, все характеристики исследуемой задачи являются кеплеровскими орбитами. Поэтому всегда существует набор эллиптических орбит, наклоненных к экватору в некотором заданном диапазоне углов, для которых будет меняться только величина 13 = ф0. Такие орбиты будут образовывать кольца конечной толщины. Эту модель можно дополнять различными нестационарными или неосесимметричными возмущениями, используя при вычислении а и b интегралы движения (33) и (34), ответственные за изменение потока во времени и по азимутальному углу ф.

Другой пример можно получить без вывода уравнений, опираясь лишь на тот факт, что все характеристики данной задачи представляют собой кеплеровские орбиты. Одним из типов кеплеровских орбит является гиперболическая орбита, одна из асимптотик которой совпадает с осью z, проходящей через центр тяготеющего тела. В этом случае все такие кеплеровские орбиты, отличающиеся друг от друга лишь углом поворота плоскости орбиты, которая перпендикулярна плоскости экватора, будут собираться в джет [16, 17] . На рисунке ( Рис. 2 ) изображены характеристики такого гидродинамического потока, формирующегося у экваториальной плоскости с гиперболическими скоростями и собирающимися в джет у оси, перпендикулярной z = 0, на некотором удалении от этой плоскости. Это означает, что при аккреции вещества на компактный объект, если скорость вещества при движении его к центру будет иметь хотя бы небольшую скорость в ортогональном к радиальному направлению, то она перейдет на гиперболическую траекторию движения, уходящую от компактного объекта. Конечно, в такой модели следует объяснить – почему асимптотика всех гипербол лежит вдоль оси диска. Для этого следует привлекать другие идеи. При формулировке сложных моделей учитывают множество факторов, в том числе и диссипативные эффекты, релятивистские, а так же наличие различных электромагнитных полей [1, 2, 4] . Но в грубом приближении модель, по всей видимости, дает простое описание общей идеи возникновения джетов. Уравнение кеплеровских орбит, представленных на рисунке ( Рис. 2 ), имеет следующий вид:

х = t cos фо, у = t sin фо, z =-(-kt2 + ct), где c и k — интегралы движения, одинаковые для всех характеристик. Отдельные характеристики отличаются только значением интеграла движения ф0.

Эта модель иллюстрирует процесс формирования джета у массивных, но очень компактных объектов. Эту модель можно дополнять возмущениями во времени и по углу. Хотя в такой модели нет особой новизны, но во многих работах часто упускают такую возможность объяснить возникновение джетов с помощью простых кеплеровских орбит, пусть и в упрощенном виде.

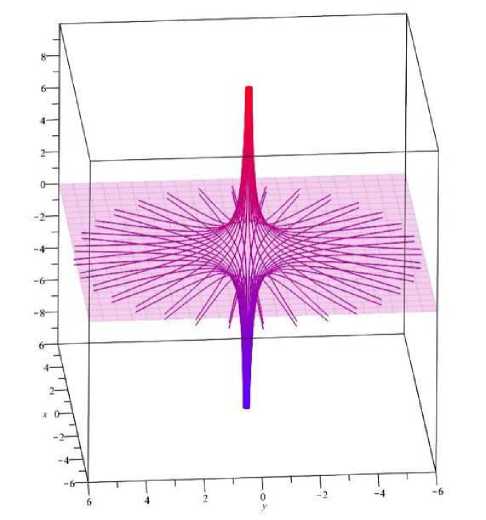
Рис. 2. Простая модель формирования джета. Линии тока пыли представляют собой гиперболические орбиты Кеплера.

10.    Эволюция плотности пыли

Описание динамики плотности пыли, в рамках данной задачи, строится на основе метода маркеров, изложенного в первом разделе данной работы. Маркерные функции e^a(x,t) представляют собой любые три независимых интеграла движения вдоль характеристик, поскольку соотношения ( 3 ) на характеристиках эквивалентны уравнениям:

dea

— = 0, а = 1, 2, 3.                                     (39)

at

Следовательно, общий вид маркерных функций, который необходимо извлекать из начальных и граничных условий, можно для случая динамики вблизи плоскости экватора записать в следующем общем виде:

e ^a = е^а(т,ф,^ = E ^a (h,l 2 ,l 3 ,l 5 ), а = 1,2, 3.

Для вычисления явной зависимости маркерных функций от координат и времени в функции E ^a следует подставить зависимость функций а(г, ф, t) и Ь(г, ф, t) от координат и времени, полученную из решений уравнений ( 35 ). После вычисления такой зависимости, плотность p вычисляется из соотношения ( 5 ). При этом следует учесть, что для распределения плотности вдоль экваториальной плоскости в предположении малости скоростей вдоль оси z соотношение ( 5 ) следует заменить на соотношение следующего вида:

/ de ¹ de ¹ \

p = det

Эх Эе2

дх

ду де²

дУ

,

где функции е 1 (х, у, z), и е ² (х, у, t) вычисляются из соотношений ( 40 ).

В некоторых случаях получить решение задачи о распределении плотности и динамике пыли можно непосредственно решая уравнение неразрывности. Например, в случае стационарной радиальной задачи, когда вещество радиально падает или удаляется от компактного объекта, проще решать уравнение неразрывности ( 2 ). Для этого случая 1 1 = 0 и полагая: p = р(г), уравнение неразрывности приводим к следующему виду:

дГ (^bxp^ = 0.                                        ⁽⁴²⁾

Это уравнение после приведения к уравнению по координате г принимает такой вид:

^г1Г    ^+3bp =0.

Интегрируя это уравнение, находим:

= po = ______po______ p   Г3,   V2rVl2r2 + 2рг’ где p0 — постоянная интегрирования. График этой функции не сильно отличается от кривой г-2, особенно на больших расстояниях. Поэтому здесь он не приводится. В случае осесимметричных течений, соответствующих (38), непосредственно уравнение (42) использовать нельзя, поскольку производные по z вблизи плоскости z = 0 имеют очень большие значения. Поэтому пренебрегать скоростью вдоль z в этом случае невозможно. Анализ этой задачи выходит за рамки данной небольшой работы.

11.    Заключение

В работе рассмотрена общая задача описания динамики пыли вблизи тяготеющего центра. Найдены интегралы движения в явном виде для движения пыли в плоскости z = 0. На основе полученных решений в качестве простых примеров предложены модели описания дисковых колец у компактных объектов, а также джетов. Предложенный метод предлагает возможность представлять простым и наглядным образом часто наблюдаемые вблизи астрофизических объектов явления. Это может дать более глубокое понимание сложных процессов, происходящих в реальности близи компактных астрофизических объектов. В работе остались без внимания важные варианты описания нестационарных и несимметричных по угловой переменной процессов. Они требуют отдельного более сложного анализа, что выходит за рамки данной работы. Полученные результаты могут использоваться в образовательных целях при преподавании курсов астрофизики.