Динамика ротора на комбинированных опорах с центробежными переключателями

ческих топливных элементов электромобилей, турбодетандеры и различные виды насосов для криогенной техники и нефтехимической промышленности) актуальна задача обеспечения повышенной надежности, что предъявляет более жесткие требования к опорным узлам роторов такого рода машин. И когда ни один из существующих видов подшипников не удовлетворяет техническим требованиям роторной машины, как возможное решение данной проблемы рассматривают вариант совмещения опор различного принципа действия для повышения надежности опорного узла за счет разделения и дублирования функций подшипников. Одним из вариантов является совмещение в едином опорном узле подшипников качения и скольжения по различным пространственным схемам, что позволяет использовать достоинства и исключить недостатки, присущие каждому виду опор на различных режимах работы. Конструкции комбинированных опор и принципы их действия повышают надежность опорного узла за счет разделения и/или дублирования функций подшипников на различных режимах работы, что приводит к выполнению основных критериев работоспособности даже при существенном ужесточении эксплуатационных требований к опорным узлам.

Выделяют два принципиально различных способа построения комбинированных опор: разделение нагрузок или разделение скоростей [1–6] (рис. 1), также существуют варианты, когда одна и та же конструкция может работать как в режиме разделения скоростей, так и в режиме разделения нагрузок [7]. Принцип работы комбинированной опоры, функционирующей по принципу разделения нагрузок (КОРН), заключается в том, что на основном рабочем режиме ПК работает с меньшей нагрузкой по сравнению с его одиночной постановкой. Разгрузка ПК осуществляется за счет возникновения гидродинамических или гидростатических реакций ПС (рис. 1а). Комбинированная опора с разделением скоростей (КОРС) обеспечивает вращение ротора в режиме пуска-останова в ПК, а по мере увеличения скорости вращения и роста реакции ПС, опора качения из работы выключается и передача нагрузки на корпус осуществляется через смазочный слой ПС (рис. 1 б,в).

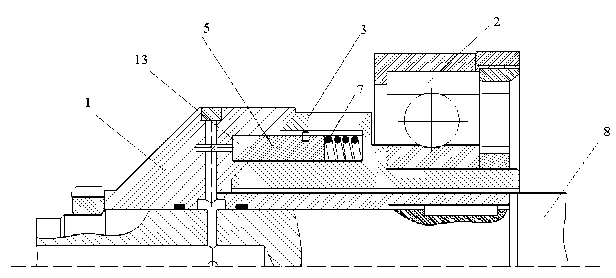
Для перспективных высокоскоростных роторных машин с линейными скоростями на поверхности цапфы ротора порядка 102 м/с и выше наиболее перспективной является применение комбинированных опор по последовательной схеме расположения относительно оси вала и работающих по принципу разделения скоростей (КОРС). Например, в опоре ротора турбонасоса МК48 для перекачки жидкого кислорода корабля многоразового использования Shuttle [3] применена постоянно включенная КОРС, обеспечивающая стабильную работу роторно-опорного узла при частоте вращения 95000 об/мин (210 м/с) (рисунок 2а). Отечественными учеными была предложена адаптивная КОРС с переключением по давлению [8] с рабочей частотой вращения 10000 об/мин (75 м/с) (рис. 2б). Вместе с тем мож- но говорить о том, что применение комбинированных опор носит экспериментальный характер и отсутствуют единые методики их расчета и проектирования. При этом количество изобретений по классу МПК F16 C21/00 «Комбинации из подшипников скольжения с подшипниками качения» насчитывает тысячи единиц, в которых описываются положительные качества и предпосылки проектирования такого вида опор [9-12].

Механизм работы КОРС предполагает следующие направления улучшения рабочих характеристик опорного узла:

• 1)    уменьшение повреждающих моментов, действующих на втулку подшипника скольжения во время переходных режимов, что ведет к повышению его ресурса;

• 2)    уменьшение центробежных нагрузок в подшипнике качения за счет разделения скоростей;

• 3)    отстранение от режимов самовозбуждаю-щихся колебаний, характерных движению роторов в подшипниках скольжения: во время неустойчивого движения ротора опасность существенных повреждений (например, заклинивания цапфы во втулке ПС) практически исключается за счет возможности дополнительного поворота в ПК;

• 4)    повышение возможностей обеспечения необходимых динамических характеристик опорного узла для обеспечения прохождения резонансных режимов с допустимыми амплитудами колебаний;

  
  
  
  

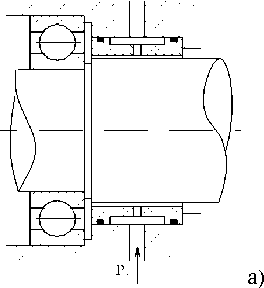
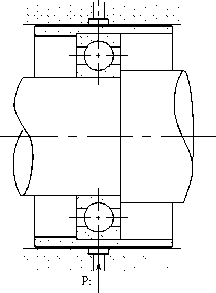
  Рис. 1. Схемы комбинированных опор

  
  
  
  
  
  

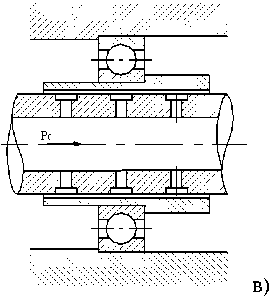
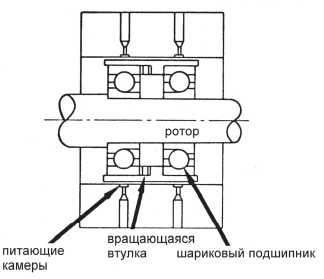
  a)

  
  
  

  б)

  Рис. 2. Конструкции комбинированных опор

  
  

• 5)    повышение надежности опорного узла за счет повышенной работоспособности опорного узла в аварийных ситуациях и при неустойчивой работе за счет дублирования функций ПК и ПС;

• 6)    отстройка от режимов турбулентности за счет адаптивного перераспределения скоростей между подшипником качения и скольжения.

Цель работы: обоснование положительных эффектов для КОРС с центробежным переключателем в виде упругого лепестка теоретическими и экспериментальными методами. В работе рассматривается комбинированная опора [13], схема которой представлена на рис. 3. Комбинированная опора работает следующим образом:

• 1)    в момент пуска машины передача нагрузки на корпус 1 происходит через подшипник качения 2 и упругие лепестки 4, которые за счет предварительной деформации центрируют вал 3;

• 2)    по мере увеличения частоты вращения упругие лепестки отгибаются от поверхности подшипника качения за счет центробежных сил, наружное кольцо ПК начинает проскальзывать относительно поверхности лепестков;

• 3)    при достижении определенной частоты

вращения (назовем ее частотой переключения ю _пер ) когда центробежные силы станут настолько велики, что превысят силы упругости от предварительной деформации произойдет полное расцепление лепестков и наружного кольца ПК, а в образовавшемся зазоре возникнет гидродинамическая реакция; нагрузка с вала 3 на корпус 1 передается последовательно через ПС и ПК, наружное кольцо ПК вращается с частотой меньшей, чем частота вращения ротора.

МЕТОДИКА ИССЛЕДОВАНИЙ

Теоретическая модель КОРС базируется на синтезе математических моделей ПК, ПС и упругого лепестка и выработке условий сопряжения на различных этапах работы КОРС. Для оценки работоспособности опорного узла, как правило, достаточно знать его реакции, предельную грузоподъемность, потери мощности на трение, расход смазочного материала, тепловой режим, коэффициенты жесткости и демпфирования.

Математическая модель радиально-упорного подшипника качения (рис. 4) основывается на

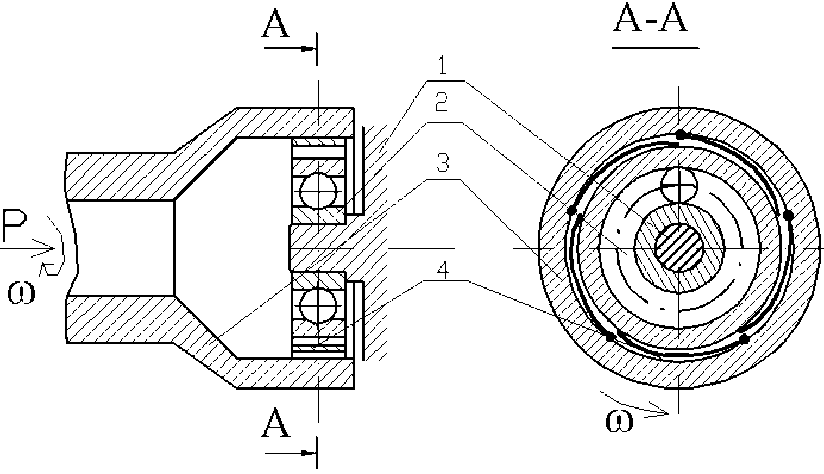
Рис. 3. Схема комбинированной опоры с центробежным переключателем

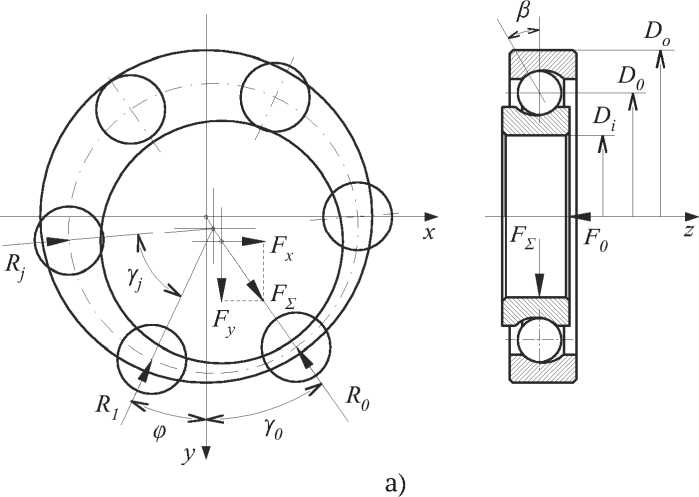
Рис. 4. Схема шарикового радиально-упорного подшипника качения (а) и эпюра распределения нагрузок между телами качения (б)

б)

решении контактной задачи теории упругости [14, 15] и строилась при следующих допущениях:

• . рассматривается подшипник с идеальными геометрическими параметрами: отсутствуют микронеровности, отклонения от формы всех деталей ПК;

. материалы контактирующих тел однородны по своим механическим свойствам и абсолютно упругие;

. нагрузка приложена перпендикулярно поверхности контакта;

. деформации в контакте малы по сравнению с размерами площадки;

. не учитывается влияние гидродинамических сил в смазочном слое между поверхностями тел качения и колец подшипника.

. Реакция со стороны тел качения в зависи- мости от смещения центра внутреннего кольца в направлении координат X, Y, Z

R™ = Kx^^ ^(tgpsmpcosy₀ + cospcosyj + tgy₀cos/?sinyj) ^cospcosyj ;

R™ = Ky^ ^(tg/?sin/? s iny0 + ctgy0cos/?cosyy + cos^sinyy) ^cos^sinyy;

R™ = Kz’k (sin/? + ctg/?cos/?cosy₀cosy, + ctg/?cos/?siny₀siny_y) ²sin/j'.

где                – коэффициент пропор- k З^Р '2

циональности, зависящий от материала и формы контактирующих поверхностей, его можно охарактеризовать как коэффициент нелинейной жесткости подшипника качения размерностью

k

Н/м3/2, здесь     - величина являющаяся ото бражением геометрии контакта и определяемая в зависимости от вспомогательной величины

;

- сумма главных кривизн поверхностей соприкосновения тел в месте их первоначального контакта;

- коэффициент, характеризующий упругие свойства материала, здесь                - соответствен но, коэффициенты Пуассона и модули упругости материалов контактирующих тел;

- деформация от предварительного натяга.

Математическое описание сил трения основывается на полуэмпирической методике [16]

p 0.55

M™ = M(F) + M((n) = 0S-l(T⁶\-^\ X \L₀/

X (3F_a - 0.1F_r)D₀ + 2 • 10-¹⁰O)^2/3D₀³ , (2)

где – эквивалентная нагрузка на ПК; Fr, Fa - радиальная и осевая нагрузка, приведенные к подшипнику; X, Y - коэффициенты, учитывающие разное повреждающее действие радиальной и осевой нагрузки, опре- деляются в зависимости от соотношения Fr /C0, здесь C0 - статическая грузоподъемность ПК; V - коэффициент вращения; KБ, KТ - коэффициенты безопасности и температуры; v - кинематическая вязкость смазки; n – частота вращения.

Математическая модель гидродинамического подшипника основывается на классических постулатах гидродинамической теории смазки.

Определение сил гладкого гидродинамиче- ского и гидростатодинамического с точечными камерами подшипников (рис. 3) основывается на интегрировании поля давлений p(x, z) по опорной поверхности на основании решения уравнения Рейнольдса

, (3)

Эх LpKx SxJ dz LpKz dzj Эх             r \ x где - функция радиального зазора; p, ц - плотность и динамическая вязкость смазки; U, V – скорость смазочного материала на поверхности цапфы в окружном и радиальном направлении.

Реакции и момент трения подшипника сколь- жения

L nltD

;

о J

L

И лО

;

о J

- ,пс       D rL rnD ,, ,

;

ip         2

h dp pU

2 ox h

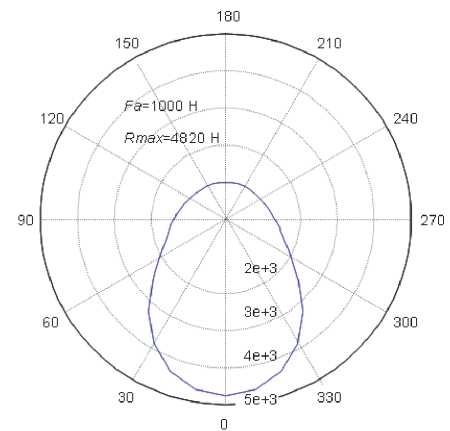
Реакция ПС находится из решения уравнения Рейнольдса [17, 18], расчетная схем гидростатодинамического подшипника с точечными питающими камерами представлена на рис. 5а, на рис. 5б представлен пример расчета поля давлений.

Температура в смазочном слое определяется на основании численного решения уравнения баланса энергий

ph-Cp

QT dT (U dt ⁺ dx \2

/i² dp\

12pKx dx/

dT / h? dp\ dz \12pKz dz /

£p + ^ ^E + ^y2^

dt 2 dx h

Решение уравнения баланса энергий совместно с решением уравнения Рейнольдса позволяет определить температуру смазочного слоя и скорректировать вязкость смазочного материала. Решение уравнений выполняется численными методами в итерационном цикле с пошаговой корректировкой по давлению, температуре и вязкости смазочного материала.

В качестве смазочных материалов для проведения численных экспериментов были выбраны жидкий водород и кислород. Аппроксимация теплофизических свойств проводилась путем по-

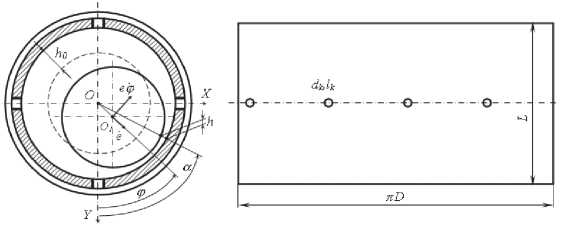
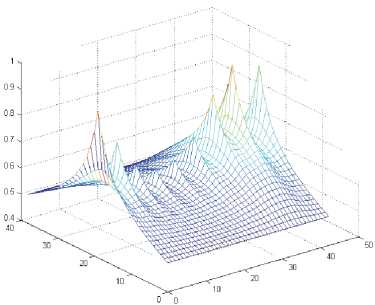
Рис. 5. Схема радиального гидростатодинамического подшипника (а) и расчетное поле давлений (б)

б)

строения 3-х мерных поверхностей зависимости вязкости и плотности от температуры и давления по табличным данным [19].

Для водорода (H ₂ ), температура T =10 – 40 К:

• -    динамическая вязкость Па х с;

• -    плотность , кг/м ³ .

Для кислорода (О ₂ ), температура T= 90 – 130 К:

• -    динамическая вязкость Па х с;

• -    плотность кг/м ³ .

Математическая модель лепестка базировалась на конечно-элементном анализе упругой криволинейной балки в системе автоматизированного проектирования APM Win Machine [20]. Расчетная схема лепестка представлена на рисунке 6а. Схема нагружения лепестка (рисунок 6б) менялась согласно имитационной модели работы КОРС: на этапе разгона действуют силы упругости от начальной деформации лепестка и центробежные силы; на основном режиме работы действуют сила упругости лепестка, центробежные и гидродинамические силы. Суммарная деформация лепестка определялась на основании принципа суперпозиции от каждой действующей силы.

Синтез математических моделей заключается в составлении условий сопряжения для рабочих характеристик опорного узла, следующих из принципа функционирования каждого вида комбинированных опор.

Грузоподъемность КОРС:

• -    на этапе разгона РУ^корс = И^^пк;

  

  Рис. 6. Конечно-элементная схема упругого лепестка (а) и схема нагружения (б)

  
  
  
  
  

  - на переходном режиме РИ^корс = РИ^УЛ, здесь 1У^ул - грузоподъемность упругого ле-

• пестка;

• -    на основном режиме И/^корс = W^nc.

Момент трения (коэффициент трения, потери мощности на трение):

• - на этапе разгона М^^РС = М™;

  - на переходном режиме М^^РС = М^ул, здесь М^ул - момент трения скольжения при проскальзывании упругого лепестка относительно

наружного кольца ПК;

- на основном режиме М^®РС = М^рс.

Расход смазочного материала через комби- нированную опору:

, где QnK, QnC - расход смазочного материала через ПК и ПС, соответственно;

– коэффициенты гидравлического сопротивления ПС и ПК, соответственно.

Так как ПК на основном режиме вращается на скоростях близких к нулю и основные факторы его нагрева исключены можно дать рекомендацию о его температура не будет существенной, то можно дать рекомендации о применении в составе КОРС ПК со встроенными уплотнения, что позволит более быстро переходить в режим полного разделения скоростей и тогда расход смазочного материала будет определяться только геометрией щелевого канала ПС.

Температурный режим комбинированной опоры:

• -    на этапе разгона t^K0PC = С^пк, здесь С^пк -температура ПК;

• -    на переходном режиме t^K0PC = t^nK + (^ул , здесь t^Yn - температура нагрева лепестка от проскальзывания поверхностей упругого лепестка относительно наружного кольца ПК;

• -    на основном режиме t^K0PC = t^nc.

Жесткость комбинированной опоры:

Г^КОРС _ КпКк™

• -    на этапе разгона К = _Пк_+кул , здесь /<^пк- жесткость ПК, К^УЛ - жесткость упругого лепестка;

корс к^пск^у;1

• -    на переходном режиме К = _кпс_+кул , КОРС _                         ⁺

здесь К      — _кпс_+кул , - жесткость ПС;

rzKOPC КПСКУЛ

• -    на основном режиме К = _Пс_+кул •

Демпфирующие характеристики комбинированных опор с достаточной обоснованностью определяется смазочным слоем ПС, т.к. демпфирование в ПК и в упругом лепестке на несколько порядков ниже даже для маловязких жидкостей [15].

г> КОРС   о УЛ        о УЛ

• -    на этапе разгона В = В , здесь - демпфирование упругого лепестка, которое определяется внутреннем трением в материале и конструкционным трением;

• -    на переходном и основном режимах В^корс _ руд + В^пс, здесь В^пс - демпфирование ПС.

Коэффициенты жесткости и демпфирования для ПК и ПС определяются в квазистационарной линейной постановке [21, 22].

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

В результате совместного решения уравнений теории упругости и гидродинамической теории смазки были получены следующие результаты. Особенности взаимовлияния силовых факторов обуславливают нетривиальные эффекты повышения рабочих характеристик КО.

На основании разработанной математической модели был проведен ряд вычислительных экспериментов для следующих параметров роторно-опорного узла:

• -    диаметр вала d= 40 мм;

• -    частота вращения 0...10000 об/мин;

• -    смазочная среда - жидкий водород;

• -    толщина лепестка 5 =100 мкм;

• -    ширина лепестка b =72 мм;

• -    длина лепестка l =18 мм;

• -    радиус лепестка r =41 мм;

• -    давление подачи смазочного материала: р₀ =2,5 атм.

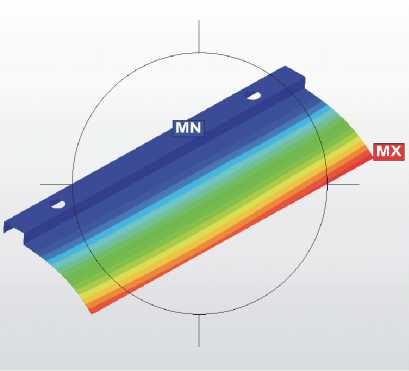
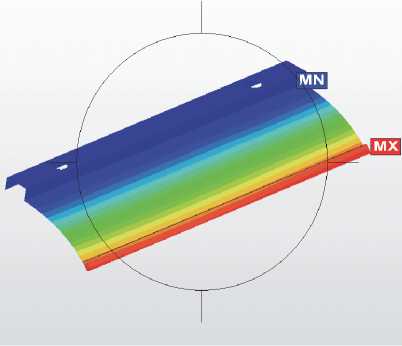
Особенность работы многолепесткового подшипника в КОРС состоит в том, что на основном режиме на него действует поле гидродинамического давления, с одной стороны, и поле центробежных сил с другой стороны (рис. 7а). Это создает предпосылки для управления зазором лепесткового подшипника на основном режиме, например, путем применения утяжелителей, которые могут быть размещены на нерабочей стороне лепестка (рис. 7б). Также можно снизить чувствительность лепестка к перепадам гидродинамического давления в результате колебаний ротора.

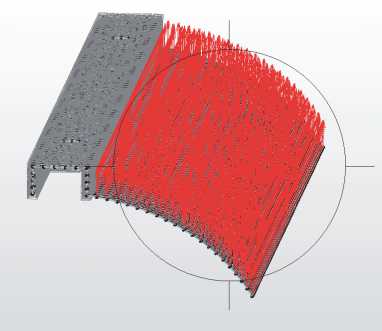
На рис. 8 представлены результаты численного расчета деформации лепестка под действием центробежной силы и гидродинамического давления. Можно говорить о том, что варьируя геометрическими параметрами лепестка можно добиться на основном рабочем режиме требуемого радиального зазора (рис. 8а). Причем, применение утяжелителей, закрепленных на краю лепестка, позволяет усилить этот эффект, например, для малых скоростей (рис. 8б). Это позволит использовать преимущества лепестковых подшипников в опорных узлах, работающих на смазочной среде с начальной вязкостью порядка Па х с.

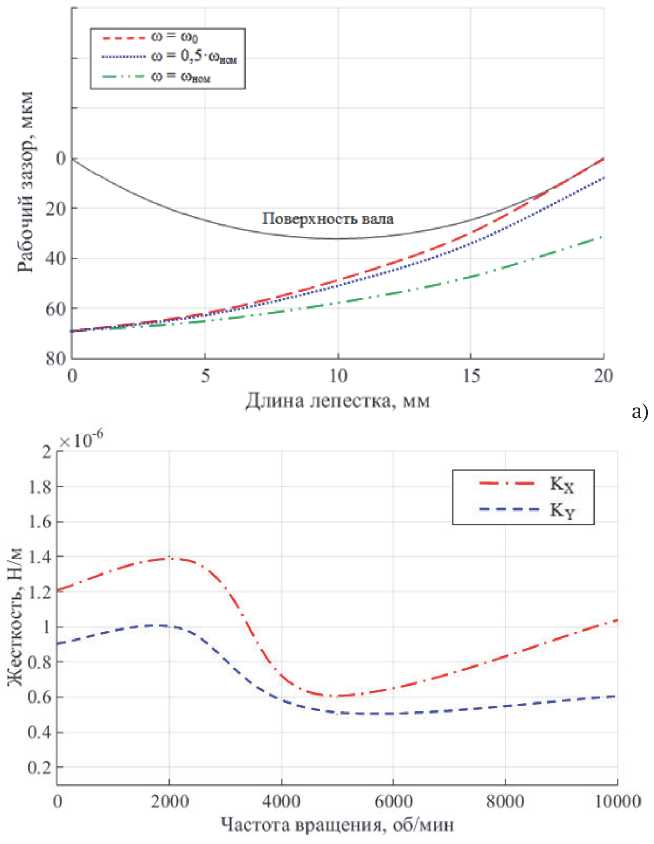
На рис. 9а представлена имитационная схема деформации лепестка в зависимости от скорости вращения, которая наглядно показывает как изменяется зазор лепесткового подшипника на переходном режиме. На рис. 9б представлена зависимость жесткости КОРС с центробежными

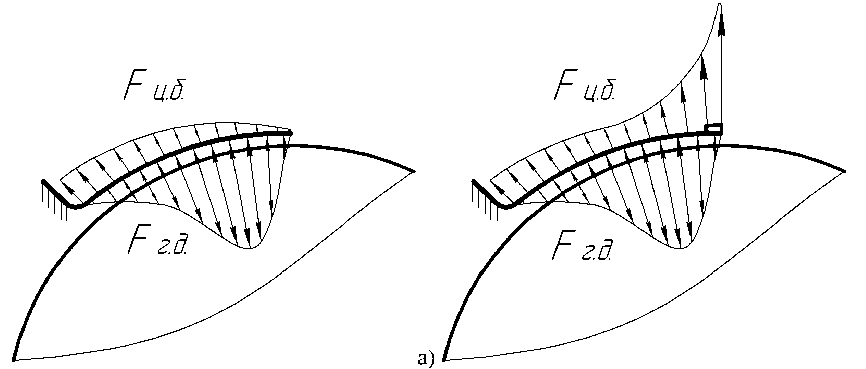
Рис . 7. Сложнонагруженное состояние лепестка в КОРС

‘ 1 б)

Рис. 8. Динамическая модель КОРС

б)

Рис. 9. Динамический изгиб упругого лепестка (а) и коэффициенты жесткости (КОРС) (б)

переключателями от угловой скорости. Анализируя представленные результаты, можно сказать, что на начальном этапе эквивалентная жесткость опорного узла растет, что связано с тем, что под действием центробежных сил упругий переключатель становится жестче. В тот момент, когда происходит отрыв лепестка от поверхности подшипника качения жесткость КОРС определяется жесткостью смазочного слоя, а так как в этот момент зазор весьма мал, то и жесткость смазочного слоя велика. С дальнейшем увеличением скорости зазор увеличивается – жесткость смазочного слоя и, соответственно, всей КОРС падает, а с дальнейшим ростом скорости растет.

Особенность жесткостных характеристик КОРС также заключается в том, что эквивалентная жесткость всего опорного узла не может быть больше жесткости самого податливого из ее элементов. То есть с увеличением угловой скорости жесткостная характеристика будет асимптотически приближаться к этому значению.

Такое сложное динамическое поведение опорного узла на переходном режиме накладывает ограничения при проектировании роторноопорного узла и требует определения множества критических частот на каждом из этапов разгона.

Используя полученные значения коэффициентов жесткости для проведения модального анализа [23] можно построить диаграмму Кэмпбелла (рис. 10). Скачок коэффициентов жесткости КОРС на этапе разгона приводит к скачку собственных частот, что приводит к появлению точек пересечения с частотой возбуждения и возникновению резонансных явлений на переходном режиме, на этапе останова происходят те же явления. Данная особенность требует более тщательного анализа поведения ротора на КОРС на переходных режимах и учета этого явления при выборе характеристик совмещаемых подшипников.

ВЫВОДЫ

Проведенный анализ результатов позволяет сделать вывод о существенных преимуществах применения комбинированных опорных узлов в агрегатах с тяжелыми условиями для работы подшипников: позволяет повысить ресурс опорного узла, повысить грузоподъемность, быстроход- ность, улучшить динамические характеристики с позиций уменьшения уровня вибраций и отстранения от режимов критических частот. Но достижение перечисленных положительных эффектов КО по сравнению с одиночной постановкой ПК или ПС возможно лишь в случае правильного выбора геометрических параметров опорных узлов при заданных рабочих (частота вращения, внешняя нагрузка, дисбаланс ротора, рабочая среда, температура, давление). Например, ПК для КОРС, выбранный только с позиций удовлетворения заданной геометрии конструкции может не обеспечить необходимые динамические характеристики всего опорного узла, выбор гидродинамического подшипника вместо гидростатического при низкой вязкости смазочного материала может не обеспечить режим разделения скоростей и т.п.

Все это ставит задачи о разработке методик проектирования комбинированных опор, алгоритмов выбора оптимальных параметров и, что самое главное, выявление границ рационального применения принципа совмещения опор качения и скольжения в едином узле. Процесс проектирования комбинированной опоры заключается в анализе возможностей изменения существующей конструкции с целью введения в опорный узел комбинируемого подшипника, оценки статических, динамических характеристики и ресурса нового опорного узла, корректировку геометрических параметров с целью выполнения критериев прочности, износостойкости и виброустойчивости.

Можно сделать вывод о том, что комбинирование подшипников качения и скольжения дают

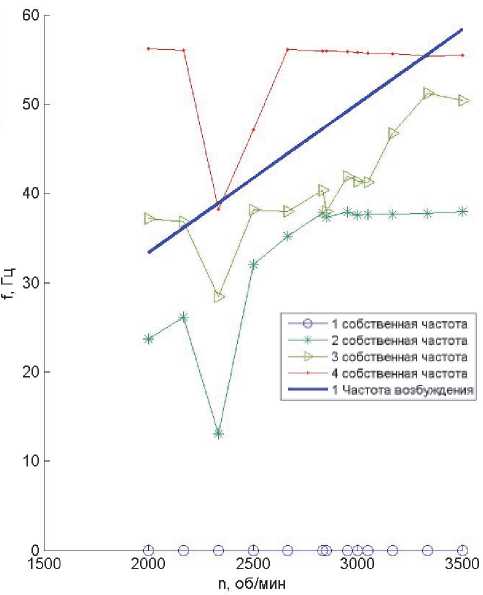
Рис. 10. Характерная диаграмма Кэмпбелла для ротора на КОРС

большую гибкость при выборе геометрических параметров комбинируемых подшипников на этапе проектирования для обеспечения необходимых статических и динамических характеристик всей роторно-опорной системы. Усложнение конструкции опорного узла и, связанные с этим, сложности изготовления и неудобства монтажа требуют оценки с учетом экономических затрат и опытом эксплуатации в реальных турбомашинах. Необходимо отметить, что несмотря на очевидные преимущества комбинированных подшипников и наличия достаточно большого числа патентованных конструкций эволюция инженерных решений в данной области идет достаточно медленно и осторожно. Это связано с малоизученностью комбинированных опор, отсутствию методик и практического инструментария для их проектирования.

Обобщая все вышесказанное, можно отметить перспективность применения комбинированных опор в высокоскоростных роторных машинах с электрическим и турбинным приводом в агрегатах энергетической, автомобильной, авиационной и ракетно-космической техники.