Динамика синхронизации двухкаскадного генератора ван дер Поля

Модели в форме взаимосвязанных осцилляторов (активных и консервативных) находят достаточно широкое применение. Причем они используются как для исследования реально существующих объектов [1–3], так и для обнаружения и изучения новых физических эффектов [4–6].

Одним из способов взаимосвязи осцилляторов является их кольцевое соединение. При этом в кольцевом генераторе (КГ) цепь положительной обратной связи, обеспечивающей генерацию, существует лишь при замыкании кольца активных ячеек, каждая из которых обратной связи не содержит и не является самогенерирующей. Было показано [7], что КГ позволяет получить сигнал с повышенной долговременной стабильностью частоты по сравнению с автогенератором, реализованным на отдельно взятой ячейке. В статье [8] рассмотрен вариант КГ – кольцо из двух резонансных ячеек (каскадов) с кубически нелинейными активными трехполюсниками. Этот вариант КГ назван двухкаскадным генератором (осциллятором) ван дер Поля. Исследованы характеристики его автономных колебаний. В настоящем сообщении рассматривается режим синхронизации этого генератора внешним гармоническим сигналом. Исследование проведено в рамках дискретно-временной (ДВ) модели динамической системы.

1.    ДВ-модель генератора

Структурная схема двухкаскадного генератора ван дер Поля приведена на рис. 1.

Приняв в качестве математической модели осциллятора ван дер Поля с внешним воздействием E(t) уравнение движения вида d2У1 , ®o dy1 , -a2

d ²"⁺ Q 1T^+ю0 y ¹ =

= P ^ 0 ( 1 - У 12 ) d r ⁺ ® 0 E ⁽ t ).

Q        dt

получим модель двухкаскадного генератора с идентичными ячейками в форме системы дифференциальных уравнений d2y1+^» dy1+ш2„ - dt 2 + Q dt +m°y 1 "

= p ^ ( 1 - y 22 ) dy 2 + ™ 0 E ( t ). Q        dt

d ² У 2 7^0 dy 2    2     J^0     2 dy 1

' П ' H0y2 = p   (1 - y 1 Hr■ dt2   Q dt           Q        dt

В уравнениях (1) и (2) осциллирующие переменные y_k нормированы на характерный масштаб нелинейности, to o и Q - собственные частоты добротности резонаторов ячеек, p – параметр превышения порога генерации.

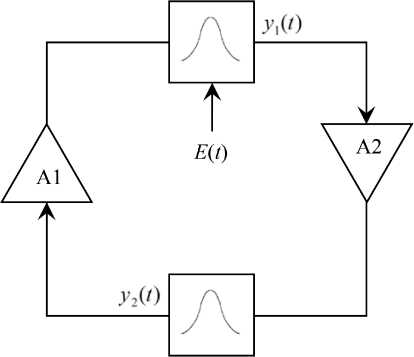
Рис. 1. Структурная схема двухкаскадного осциллятора ван дер Поля

Fig. 1. Block diagram of a two-stage van der Pol oscillator

Предполагая в дальнейшем дискретизацию времени с интервалом А , введем в уравнения (2) безразмерную временную переменную т = t / А :

—— + 2nv ^1 + 4 n2 Q2 yt = dt2       dt       01

= 2 nv p ( 1 - y 2 ) dy ²- + 4 п ² Q 0 E ( t ), d ! y 2 + 2 nv dy 2 + 4 П ² Q _g y ₂ = dt ^{2          dt}

= ^{2 nv} p ( ^{1 -} y 2 ) dy- .

dt

Здесь Q g = to g / to d - собственная частота, измеряемая в единицах частоты дискретизации to d = 2 n / А ; v = Q g / Q - полоса резонатора.

Переход к дискретному времени в (3) проведем методом работы [9]. Для осцилляций y i [ n ] = y 1 ( т n ) и y 2 [ n ] = y 2 ( т _n ) получим систему нелинейных разностных уравнений:

y 1 [ n ] - 2 6 cos ( 2 nQ _g ) y 1 [ n - 1] + 6 ² y 1 [ n - 2 ] =

= 2 nv pD ( y 2 [ n - 1], y 2 [ n - 2] ) +

+ 2 nQ _g 6 sin( 2 nQ _g) E [ n - 1],                           (4)

y 2 [ n ] - 2 6 cos ( 2 nQ g ) y 2 [ n - 1] + 6 ² y 2 [ n - 2] =

= 2nvpD (y1 [n -1], y 1 [n - 2]), где

D ( y [ n - 1], y [ n - 2 ] ) =

= ( 1 — y [ n — 1] ) ( cos ( 2 nQ g ) y [ n — 1] — y [ n — 2] )

- нелинейности ячеек, 6 = exp( -nv ) - параметр диссипации резонатора.

Систему уравнений (4) можно рассматривать с двух точек зрения. С одной из них, при выполне- нии условия Qg ^ 1 - это разностная схема для расчета автоколебаний в исследуемом генераторе. С другой, соотношения (4) определяют дискретное отображение двухкаскадного кольцевого осциллятора – динамическую систему, функционирующую в дискретном времени. Такие объекты нелинейной динамики на частотах Qg порядка частоты Найквиста вследствие эффекта подмены частот [10] демонстрируют свойства, не наблюдаемые в непрерывном времени [11].

2.    Укороченные уравнения метода ММА

Синхронные автоколебания [12; 13] в области удержания представим в форме осцилляций с медленно меняющимися комплексными амплитудами A 1 [ n ] и A 2 [ n ]:

y 1, ₂[ n ] = -A 1, ₂[ n ] Zⁿ + 2 A *2[ n ] Z ⁿ ,                     (5)

где Z = exp( j 2 nQ ) - функция частоты внешнего. Метод медленно меняющихся амплитуд (метод ММА) широко используется при решении прикладных задач теории нелинейных колебаний в непрерывном времени [14; 15]. Особенности его применения к нелинейным ДВ-системам представлены, например, в [11]. В частности, условием медленности изменения амплитуд A ^ [ n ] являются приближенные равенства A k [ n ] - A k [ n - 1] = = A k [ n — 1] — A k [ n — 2 ].

В рамках метода ММА для амплитуд автоколебаний в ячейках ДВ-осциллятора (4) при внешнем гармоническом воздействии с амплитудой E ₀ и частотой Q удается получить систему укороченных уравнений вида

A 1 [ n ] = A 1 [ n - 1] - nv ( 1 + j n ) A 1 [ n - 1] +

L 1

+ nv p I 1 — | A 2 [ n — 1] | I A 2 [ n — 1] — j nQ g E g ,

. r 1 . 4    .(6)

A 2 [ n ] = A 2 [ n - 1] - nv ( 1 + j n ) A 2 [ n - 1] +

C 1

+ nvp I 1 — — | A1 [ n — 1] | IA1 [ n — 1], где введено обозначение n = 2(Q-Qg)/ v для приведенной частоты сигнала синхронизации, а также использовано высокодобротное приближение для параметра диссипации: 6 = 1 -nv. Отметим, что для автономного осциллятора (Eg = g, Q = Qg) укороченные уравнения (6) совпадают с соответствующими уравнениями статьи [8].

В режиме установившихся колебаний в полосе удержания система разностных уравнений (6)

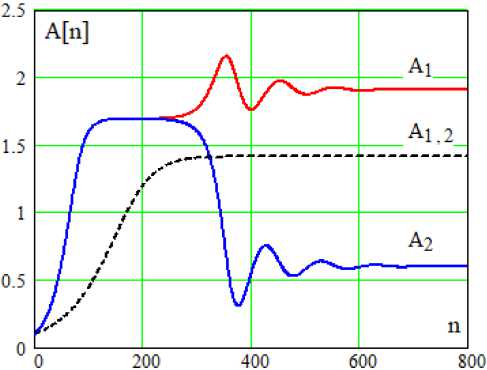
Рис. 2. Процесс установления автоколебаний

Fig. 2. Process of establishing self-oscillations

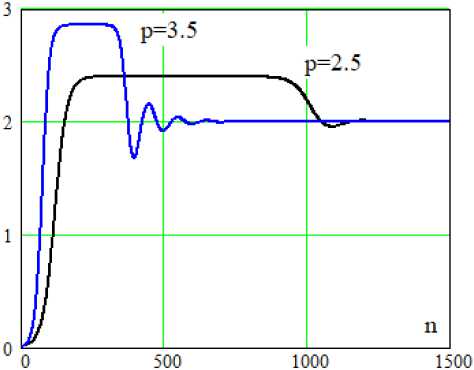
Рис. 3. Динамика суммарной мощности автоколебаний

Fig. 3. Dynamics of the total power of self-oscillations

сводится к системе нелинейных алгебраических уравнений

(

• ^v( 1 + Jn) A1 -Vp I ¹- 4 I A2 I²IA2 = - J ^0 E0 ,

  /               A

3.    Результаты моделирования автоколебаний

(

^v ( ¹ + j ⁿ ) A 2 -^v p I ¹ - 4 ¹ A I ¹ I A I = ⁰ •

Решение системы четырех действительных нелинейных уравнений (7) – технически непростая задача. Значительно проще получить решение укороченных уравнений (6) при квазистатическом изменении частоты Q . Полученные при этом зависимости A 1 2 ( Q ) будут близки к статическим частотным характеристикам.

Хорошо известно (см., например, [16]), что траектория движения автономного осциллятора (1) при выполнении условия самовозбуждения p >  1 выходит на единственный предельный цикл. Решения укороченных уравнений (6) позволяют сделать вывод о том, что для кольцевого осциллятора (2) такое поведение характерно лишь в интервале значений параметра 1 <  p <  2. При более высоких уровнях возбуждения в каскадах устанавливаются автоколебания с различающимися амплитудами [8]. Рис. 2 иллюстрирует этот эффект бистабильности для p = 3,5. Пунктирная линия на рисунке отображает динамику амплитуд автоколебаний в каскадах при p = 1,99.

Большее значение амплитуды автоколебаний достигается в каскаде с наибольшим значением начального возмущения A-[0] состояния нулевого равновесия. Если параметры каскадов различают- ся, то наибольшее значение амплитуды устанавливается в каскаде с наименьшей добротностью.

Синфазность колебаний в каскадах позволяет проводить суммирование их мощностей:

г 1 9 , , 1 9 г , W [ n ] = 2 A 1² [ n ] + 2 A 2 [ n ].

На рис. 3 представлены временные зависимости суммарной мощности W [ n ] для двух уровней возбуждения p = 2,5 и p = 3,5. Характерной особенностью является стремление W [ n ] ^ 2 для всех значений p >  2. При этом время достижения предела уменьшается с ростом уровня возбуждения.

Частотные характеристики синхронного режима колебаний в двухкаскадном генераторе (2) приведем в сравнении с аналогичными характеристиками классического генератора ван дер Поля (1). Приближенные решения системы уравнений (7) получены как решения укороченных уравнений (6) при квазистатическом изменении частоты Q синхронизирующего сигнала.

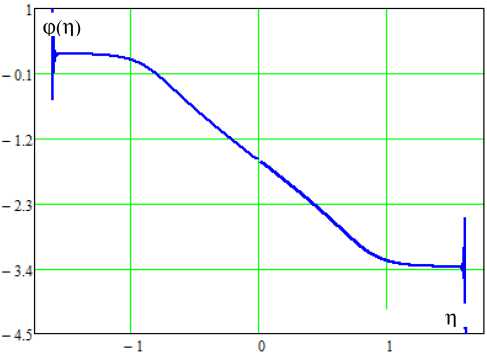
На рис. 4 представлены амплитудно-частотные ( а ) и фазочастотные ( б ) характеристики синхронных колебаний в генераторе (1) с параметрами Qo = 0,1, Q = 20, p = 1,5 при амплитуде синхросигнала Eo = 0,05. Представленные зависимости A ( n ) и ф ( n ) полностью соответствуют приведенным, например, в [17].

Характеристики синхронных колебаний двухкаскадного кольцевого генератора (2), рассчитанные для тех же значений параметров, показаны на рис. 5. АЧХ колебаний в первом (находящемся под внешнем воздействием) и втором каскадах (рис. 5, а ) различаются кардинально. Несмотря на то что при p = 1,5 в автономной системе бистабильность амплитуд не наблюдается, под действи-

^01)

а

Рис. 4. Частотная характеристика синхронизации осциллятора (1)

Fig. 4. Frequency response of the oscillator synchronization (1)

б

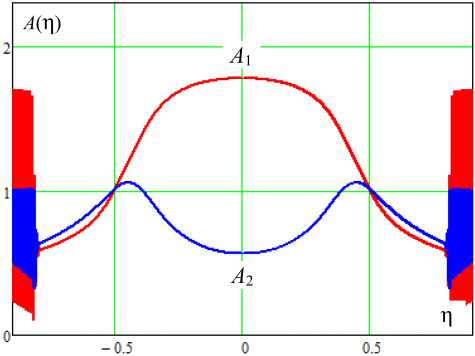
Рис. 5. Частотная характеристика синхронизации осциллятора (2): p = 1,5, E o = 0,05

Fig. 5. Frequency response of oscillator synchronization (2): p = 1,5, E 0 = 0,05

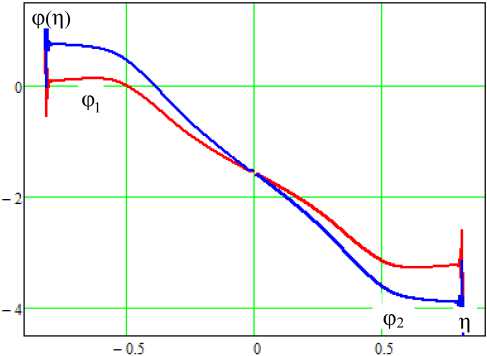
б

ем внешнего сигнала в каскадах устанавливается режим синхронных колебаний с различными амплитудами. Причем в центре полосы синхронизации (полосы удержания) амплитуда в первом каскаде выше, чем во втором. Но это соотношение амплитуд плавно меняется при приближении к границам полосы. ФЧХ синхронных колебаний в одно- и двухкаскадном генераторах (рис. 4, б и рис. 5, б ), а также колебаний в первом и втором каскадах качественно различаются незначительно.

Следует отметить, что полоса синхронизации (удержания) двухкаскадного генератора (2) при прочих равных существенно меньше полосы синхронизации генератора (1).

Эффект бистабильности амплитуд в автономном двухкаскадном генераторе (2), наблюдаемый при уровнях возбуждения p >  2, существенным образом сказывается на частотных характеристиках синхронизированных колебаний. На рис. 6 по-

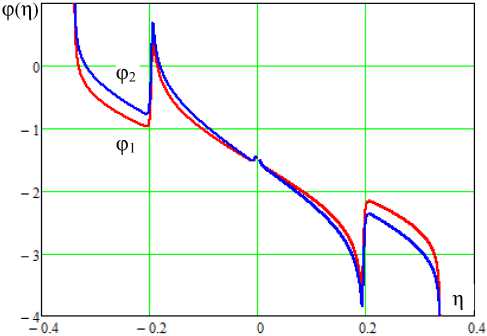
Рис. 6. Частотная характеристика синхронизации осциллятора (2): p = 2,5, E ₀ = 0,03

Fig. 6. Frequency response of oscillator synchronization (2): p = 2,5, E 0 = 0,03

казаны АЧХ ( а ) и ФЧХ ( б ) колебаний при превышении порога возбуждения p = 2,5 и амплитуде

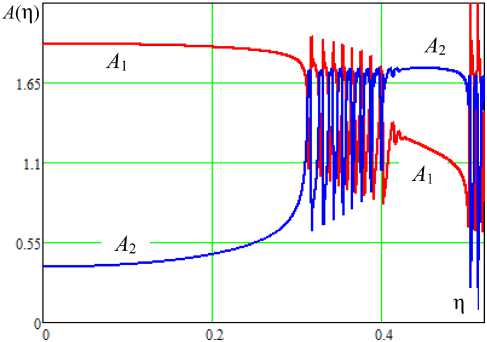
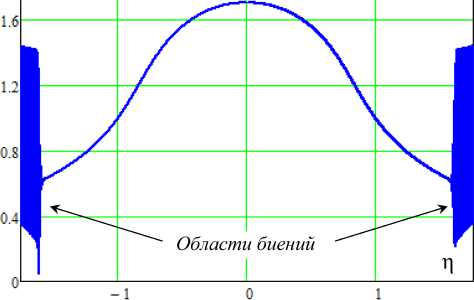
Рис. 7. АЧХ синхронизации осциллятора (2): p = 2,5, E 0 = 0,05

Fig. 7. Frequency response of synchronization of the oscillator (2): p = 2,5, Е ₀ = 0,05

синхронизации Eo = 0,03. Из рис. 6, а следует, что в каждом из каскадов могут реализоваться режимы колебаний как с высоким, так и с низким уровнем амплитуды. Смена режимов при плавном изменении частоты синхронизации осуществляется скачком.

В окрестностях частот скачков могут наблюдаться области биений, как это показано на рис. 7

с АЧХ синхронизированных колебаний под действием сигнала с амплитудой E o = 0,05. При этом область синхронизации (удержания) распадается на три подобласти – центральную и две боковых (на рис. 7 показаны только половины симметричных графиков).

Отметим также, что особенностью двухкаскадного генератора является более плоская форма центральной части графика A i = A i ( п ) (рис. 6 и 7) по сравнению с аналогичным графиком для классического генератора ван дер Поля (рис. 4).

Заключение

Представленная ДВ-модель синхронизированного двухкаскадного генератора ван дер Поля позволяет анализировать частотные характеристики колебаний в полосе удержания, форму биений в ее окрестности, процессы захвата и срыва синхронизации. Модель легко обобщается на кольцевые структуры с произвольным числом ячеек, в частности на кольцевые лазеры. Дискретное время дает возможность учета запаздывания при распространении сигнала между каскадами.