Динамика спектральных моментов раствора флуорофора

DOI:

Динамика полярной сольватации играет ключевую роль в ряде химических реакций в конденсированной фазе, особенно если среда представляет собой полярный растворитель. В качестве примеров таких реакций можно вспомнить перенос электрона [5; 7] и перенос протона [6]. Взаимодействие с диполями среды может изменять барьер реакции, тем самым напрямую влияя на скорость реакции. Более того, исследования динамики сольватации в сложных химических или биологических средах могут дать ценную информацию о локальном диэлектрическом окружении, доступ к которой в противном случае затруднен или даже невозможен. Во всех вышеперечисленных случаях детальное понимание динамики сольватации и ее зависимости от растворителя и от характеристик растворенного флуорофора имеет первостепенное значение.

Динамика растворителя может быть исследована с использованием нескольких подходов, таких как диэлектрическая дисперсия, оптический эффект Керра или эксперименты с фотонным эхом [4]. Однако одним из наиболее часто используемых подходов является метод временного сдвига Стокса. Данный метод разработан для описания соединений с флуорофорами, у которых происходит значительное изменение дипольного момента при переходе из основного в первое возбужденное состояние. При возбуждении таких молекул лазерным импульсом окружающий ратворитель начинает переориентироваться, чтобы соответствовать новому распределению заряда и минимизировать общую свободную энергию. По мере релаксации системы растворитель – флуорофор уменьшается разница свободной энергии основного и возбужденного электронных состояний растворенной молекулы, что приводит к динамическому стоксовому сдвигу (снижению частоты) флуоресцентного излучения. Эволюция системы в ходе этого процесса запечатлевается в динамике первого спектрального момента.

С другой стороны, известно, что внутримолекулярное колебательное перераспределение и колебательный перенос энергии играют решающую роль в большинстве видов фотохимических реакций [1; 3; 4; 8]. Соответственно, временные масштабы и пути релаксации колебательной энергии являются важными вопросами в фотохимии конденсированной фазы. В последние десятилетия изучение упомянутых аспектов, присущих фотохимическим реакциям, развивалось благодаря сверхбыстрым спектроскопическим методам, даровавшим экспериментаторам доступ к явлениям фемтосекундных масштабов. Детальная информация о форме и положении спектра флуоресценции позволяет произвести качественную декомпозицию экспериментальных данных на составляющие процессы.

1.    Теоретический подход

Данная работа является прямым продолжением и развитием подхода, предложенного в статье [2]. Там было детально представлено построение модели, воспроизводящей динамику первого момента спектра флуоресценции с учетом параметров возбуждающего лазерного импульса и внутримолекулярной колебательной релаксации (низкочастотной моды). Решение в рамках обсуждаемого подхода не требует использования численных методов, не вводит дополнительных упрощений или ограничений, а также позволяет проводить дальнейшие модификации и обобщения. Было показано влияние на поведение спектра длительности лазерного импульса накачки, переводящего флуорофор в возбужденное состояние. С другой стороны, на получаемую в эксперименте информацию влияет также длительность зондирующего (стробирующего) импульса [1]. Для учета его влияния на получаемый спектр можно записать выражение для зависящего от времени спектра флуоресценции как кросс-корреляционную функцию нестационарной величины:

I (w,t) = / I o (w,t

-∞

— t ) exp {- v p T 2 } d T .

Здесь vp = 1/д/2тр, tp (probe) - длительность зондирующего импульса, a I0(w,t) определяет нормированную интенсивность флуоресценции [3; 8] на частоте ω в момент вре- мени t:

I ₀ (w,t) = w ³ Z ¹ I ^ -1 (t — т ) ф (w,t, t ) d т ,

-∞

^(w,t, t ) = exp

Y (w,t — t ) ²   2 x 2    (U — Y (w,t — т)Q(t — t )) ²

Z²         ^T             2^ e (t — t ) ²

a 2 (t) = z ² / 2 ( 1 — Q ² ( t ) ) Yh²^²,

Y (w,t) = hw + E — 2E r Q(t),

Z = тeпг/оexp {—U2/с2] , где г2 = 4Er^BT, U = hwe + AG — Er, с2 = 2с2(то) = г + 2h2тe2 и E = AG + + Er - размерные константы, введенные для сокращения записи. Также используются величины: h - редуцированная постоянная Планка (далее h = 1); kB - постоянная Больцмана; T - температура среды; тe и we - длительность и частота импульса накачки

(exitation); A G - разность между энергетическими уровнями основного и возбужденного состояний электронной подсистемы флуорофора; E r - суммарная энергия реорганизации среды и внутримолекулярных колебаний.

Функция Q ( t ) содержит в себе информацию о релаксации среды и классических внутримолекулярных колебаний:

Q ( t ) = w i exp ^-Т0 + w ₂ exp ^- Т- ^ + + w ₃ exp ( — Y t ) (cos Q t + Y sin Qt^ , q = y Q 2 — Y 2 ,

где весовые коэффициенты w 1 + w ₂ + w ₃ = 1 определяют вклад каждой моды в общую энергию реорганизации; τ ₁ и τ ₂ — характерные времена релаксации, связанные с инерционными и диффузионными процессами в растворителе соответственно, а y и Q r — коэффициент затухания и резонансная частота классического внутримолекулярного колебания.

Выражение (1) представляет собой интегральную свертку сигнала флуоресценции 1 0 (w,t) и зондирующего импульса длительностью т _р , описываемого по времени гауссовым распределением. Данная операция имеет значительную вычислительную стоимость, что усугубляется решением интегралов при нахождении спектральных моментов:

M i ( t )

M ₂ ( t )

J-L ^wI(w,t)dw

^{1 (w,t)} d ^w ,

—Jw ^- ^ 1 ) ² 1 ^(w,t)dw f^^{1 (w,t)dw}

С другой стороны, в предыдущей статье [2] была представлена методика, позволяющая избежать такую проблему. Если представить I 0 ( w ,t ) как гауссову функцию от w и проинтегрировать по этой переменной, получится полином от функции Q в степени N , зависящей от порядка искомого спектрального момента. Эта функция представима как сумма из четырех экспонент, а сумма четырех слагаемых в степени N раскрывается с помощью мультиномиальной теоремы. В итоге выражение для спектрального момента после раскрытия всех скобок и приведения подобных членов представляет собой множество слагаемых, каждое из которых является интегралом по времени от гауссовой функции. Их решения можно представить в виде произведений специальной функции ошибок erfc и гауссовой экспоненты.

Для учета длительности стробирующего импульса достаточно вычислить свертку по времени результирующего выражения из [2] с зондирующим сигналом. Теперь, после введения некоторых новых обозначений, получены выражения для первых трех центральных моментов спектра флуоресценции:

^ 1 ( t ) =	F i ’ Fo ’		(7)
M 2 (t) =	F 2 ’ F o	м 2	(8)
M 3 ( t ) =	F 3 ’ Fo	зм 1 м2 - м 3	(9)

Функции F _i (t) имеют смысл начальных моментов (raw moments - сырые, грубые моменты) и вычисляются как суммы:

i

^F i (t) = ^{( —}1^ +1 7^ ^ 9 i,N   ^

N =0     k + l + m + n = N

N !

. !       ! ^ф( ‘,‘-'’”¹'" ⁾ ,

^ф(t) =

nWN       г 2/   , ,   42 ,       г Г vd Vpe VPVeJ

--------^ех Р ^{—a 3 ^(v g ^t + С з ) + t^ j erfc  --- ^а з----- 1\ , ^2V ge ^V po                                  ^2V ge ^v po       ^v pe

VgW = T-,

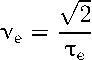
V o =       ,

ν ge

ν d

^С з = 5—, 2 ^V g

ν p ν e а з =------- ,

ν po ν ge

^V pe = У ^V P + ^V 2 ,     ^V ge = У ^V g + ^V 2 ,     ^V po = У ^V P + ^V 0 .

Здесь частоты ν e , ν g и ν d связаны с характерными временами действия возбуждающего импульса (exitation), затухания гауссовой моды (gauss) и колебательного демпфирования (damping) соответственно. Безразмерные константы а ₃ и с ₃ введены для упрощения записи. Также использованы обозначения: W = 4 E _r + as U , as = е ² /^ ² и константы, возникающие при приведении подобных слагаемых (чем старше порядок момента, тем больше этих констант):

9 2 , 2 = W ² — as e 2 / 2,

9 з , о = ^—E(E 2 + 3 e ^{2 /2)} ,

9 3 , 1 = 3 W ( E ² + е ² / 2) ,

9 3 , 2 = ^{— 3E(W 2 —} 8 ^eE‘ ^{2 /2}'⁾ , 9 з , з = W (W ² — 3c Be ² / 2) .

9 о , о = 1,

9 1 , 0 = ^{— E ,}

9 1 , 1 = W ,

9 2 , 0 = ^{E 2} + ^E 2 ^{/2 ,}

9 2 , 1 = — 2 EW ,

Вложенная сумма в выражении (10) возникает при использовании мультиномиальной теоремы. Степень N накладывает ограничение на индексы к, I, m, n таким образом, что при суммировании используются все комбинации их значений, но с условием, что их сумма равняется N . Например, для N = 2 сумма раскрывается как:

Q ^N = ^(Q 1 + Q 2 + Q 3 + Q 4 ^{) N}

k +l+ m + n = N

N ! k ! l ! m ! n !

Q k QkQ m Q n =

= Q 1 Q 0 Q 0 Q 4 + Q 0 Q 2 Q 3 Q 4 + Q 0 Q 0 Q 2 Q 0 + Q 0 Q 0 Q 3 Q 4 +

+ 2 ( Q 0 Q 0 Q 3 Q 4 + Q 0 Q 2 Q 0 Q 4 + Q 0 Q 2 Q 3 Q 4 + Q 1 Q 2 Q 0 Q 4 + Q 1 Q 0 Q 3 Q 4 + Q 1 Q 2 Q 0 Q 4 ) .

Рассматриваемые моменты имеют следующий физический смысл. Первый момент – центр тяжести (среднее значение) спектра отражает среднюю энергию излучения и несет в себе информацию об эволюции среды и классических процессах в самой молекуле флуорофора. Второй центральный момент – дисперсия спектра, характеризует разброс энергии флуоресценции. Третий центральный момент – асимметрия спектра, показывает насколько спектр скошен в ту или иную сторону и связан с анизотропией релаксации и инерционным характером эволюции вдоль координаты реакции.

Таким образом, получена конструкция, позволяющая рассчитывать зависящие от времени центральные моменты спектра флуоресценции. Используемые процедуры можно автоматизировать с помощью средств символьных вычислений и получить моменты произвольного порядка и для функции релаксации с произвольным количеством мод, но следует иметь в виду быстрый рост числа слагаемых в итоговой формуле, что может приводить к накоплению ошибок округления. Тем не менее для большинства физических приложений указанные проблемы возникать не будут.

2.    Результаты и обсуждение

Непосредственное интегрирование выражения (2) дает возможность построить динамику спектра флуоресценции. Результат численного решения представлен на рисунке 1. Слева показана развертка спектра по частоте и по времени (вид сверху), а справа вынесены срезы динамики спектра на различных этапах релаксации.

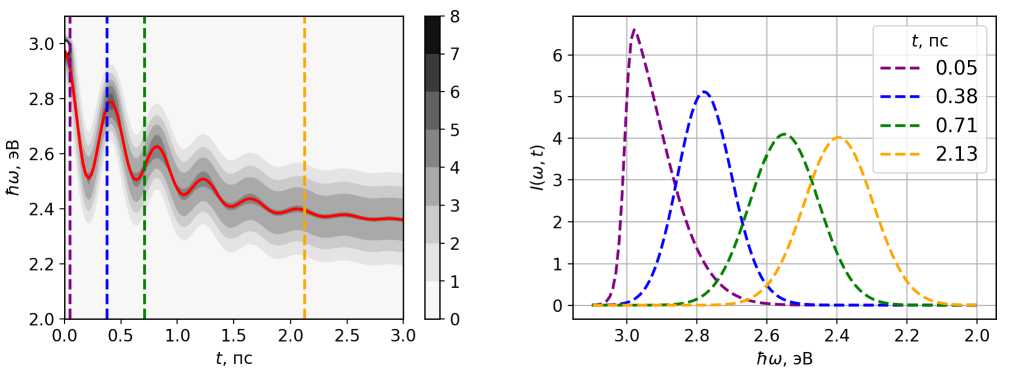
Рис. 1. Динамика нормированного по площади спектра флуоресценции. Красная линия – зависимость первого момента от времени. Цветные штриховые линии – профиль спектра в различные моменты от начала действия импульса накачки. Цветовая палитра – интенсивность флуоресценции на заданной частоте («высота» профиля спектра)

Данный расчет занимает несколько десятков секунд на ноутбуке базовой архитектуры в однопоточном режиме. При учете свертки по времени со стробирующим импульсом, длительность расчета возрастает на порядки, что повышает актуальность использования выражений (7)–(9). Вычисления по этим формулам подразумевают использование общего набора констант и функций F _i (t'), что позволяет за доли секунды получить динамику сразу нескольких спектральных моментов. При дальнейших вычислениях для параметров модели используются аргументы по умолчанию: т _е = 0 , 05 пс, т _р = 0 , 05 пс, Hw e = 3 эВ, AG = - 2 , 5 эВ, E r = 0 , 2 эВ, т 1 = 1 пс, т ₂ = 2 пс, Hy = 2 • 10 ^{- 3} эВ, Ш_г = 0 , 01 эВ и w _i = (0 , 3; 0 , 3; 0 , 4).

В предыдущей статье [2] было показано, что рост длительности импульса накачки подавляет информацию о релаксации низкочастотной колебательной моды, сглаживая осцилляции первого момента. Подобный эффект наблюдается и при повышении времени действия стробирующего импульса (рис. 2).

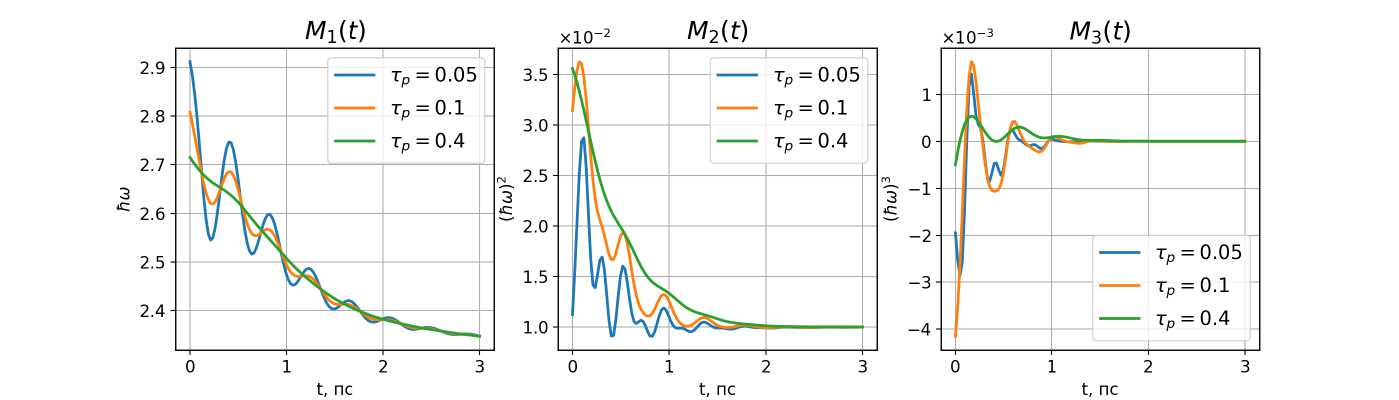
Рис. 2. Динамика центральных моментов спектра флуоресценции при различной длительности зондирующего импульса

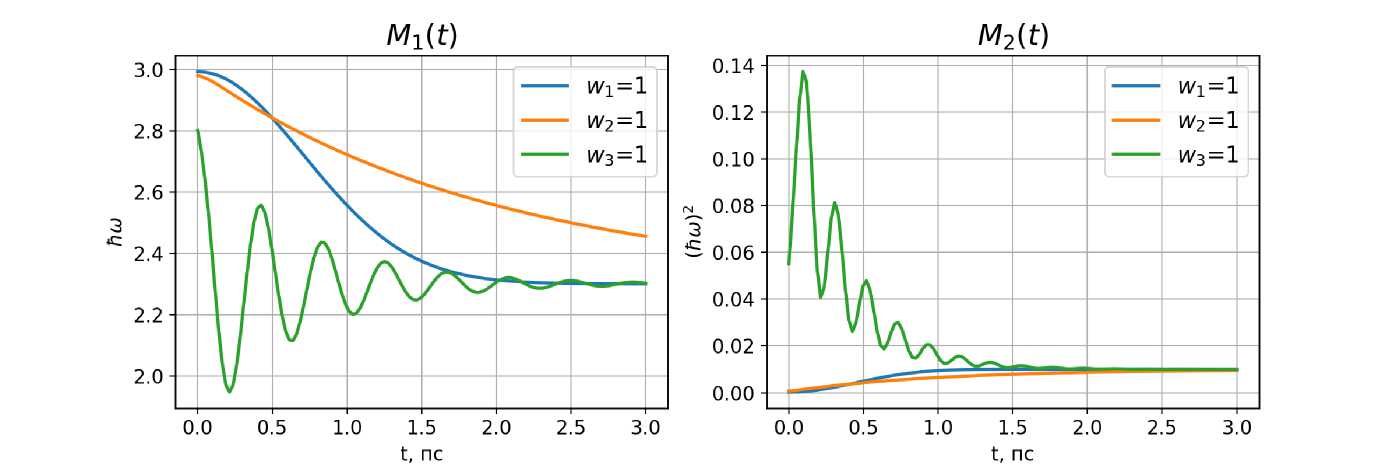
Рис. 3. Динамика первого и второго центральных моментов спектра флуоресценции в одномодовом режиме

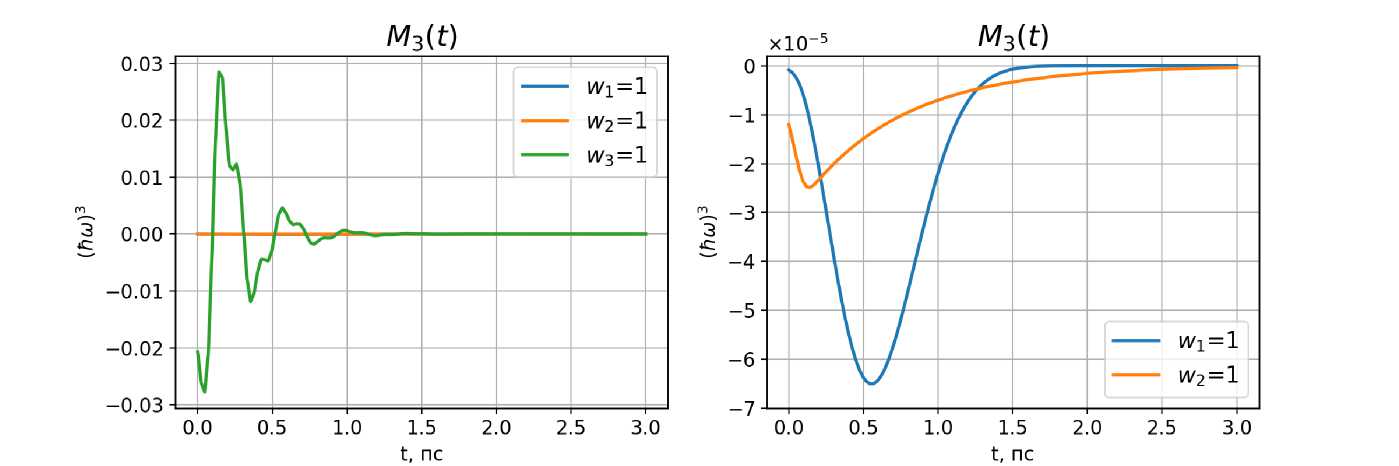
Рис. 4. Динамика третьего центрального момента спектра флуоресценции в одномодовом режиме. Графики при W 1 = 1 и w ₂ = 1 вынесены на правую панель из-за несопоставимости масштабов со случаем w ₃ = 1

Далее интересно посмотреть, как различные релаксационные процессы влияют на поведение спектральных моментов. На рисунке 3 показана динамика моментов при ва-

рьировании весов w _i в функции релаксации Q(t) таким образом, чтобы проиллюстрировать действие каждой моды по отдельности. При W 3 = 1 все остальные веса зануляются, и тогда эволюция системы полностью описывается лишь затухающей колебательной модой, отражающей релаксацию низкочастотного внутримолекулярного колебания молекулы флуорофора. При W 1 = 1 и W 2 = 1 будут активированы моды, связанные с инерционной и диффузионной релаксацией соответственно.

Примечательно, что при W 3 = 1 осцилляции наблюдаются и в динамике второго спектрального момента, то есть происходят периодические уширения и сужения спектра. Это, в свою очередь, находит отражение в поведении третьего момента (см. рис. 4).

Как видно, наибольший вклад в асимметрию спектра вносит именно внутримолекулярное колебание самого флуорофора, а эффекты среды вносят минимальную анизотропию релаксационных процессов. Этот результат довольно интересен. Предложенная ранее более полная версия модели [8], учитывающая релаксацию высокочастотных внутримолекулярных колебаний посредством описания динамики населенностей на квантовых подуровнях, страдает существенным недостатком – она подразумевает долгие вычисления, так как помимо указанных выше интегралов приходится численно решать системы неоднородных дифференциальных уравнений, описывающих кинетику населенностей. Тем не менее она позволяет анализировать реальные спектры, полученные из экспериментов, вплоть до колебательной структуры в профиле спектра, проявляющейся на ранних этапах внутримолекулярной релаксации. Для изучаемых в статье [8] растворителей и флуорофора характерно как раз поведение, которое описывается подавлением низкочастотного внутримолекулярного колебания ( w ₃ = 0). Следовательно, асимметрия спектра будет минимальна, и возникает соблазн решить обратную задачу – по времяза-висимым моментам восстановить динамику самого спектра. Это позволило бы ускорить моделирование спектра и анализ эмпирических данных.

Самым грубым приближением будет попытка аппроксимировать форму спектра нормальным распределением:

/ х 1 f (■ — M i( t ))2

Pt ic u ./ i (’x|) — . (12) n^ , ^!_x2n\ 2 / 2M 2 (t) J ^{V 7}

Информацию о третьем моменте спектра можно задействовать при построении асимметричного нормального распределения (skew normal distribution):

■   ww^exp {-(^^} (^{1 + erf} Й&1)’    ⁽¹³⁾

^( t ) = M i ( t ) — sign ( М з ( / )) У s(t)M 2 (t),

«И^ЖС» ^^—^

P( t ) ² = (s( t ) + 1M( _t ) ,

2s(t)   ^{2 / 3}

■M^.

■ ^(t) =

М з ( / ) M 2 ( t ) ^{3 / 2} .

На рисунке 5 показана форма спектра на разных временных срезах при условии отсутствия внутримолекулярного колебания (w ₃ = 0). Моменты, расчитанные по формулам (7)–(9), использовались в выражениях (12) (красные пунктирные линии) и (13) (синие штриховые линии), и полученные распределения (а точнее, их плотности вероятности) сравнивались с результатом интегрирования (2) (черные сплошные линии). На следующем рисунке 6 проиллюстрировано сравнение распределений посредством построения кривых модуля разности между плотностями вероятности статистических распределений и модельных спектров.

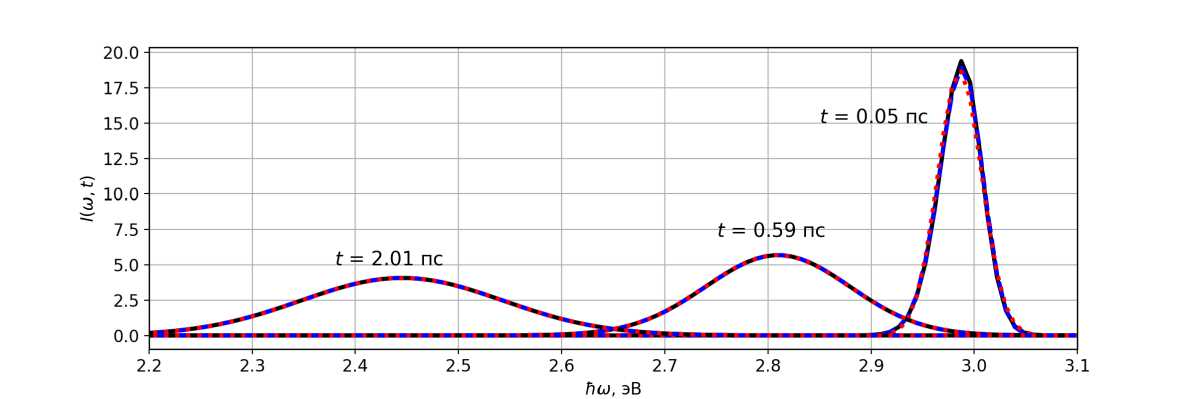
Рис. 5. Наложение нормального ( красные пунктирные линии ) и асимметричного нормального ( синие штриховые линии ) статистических распределений на результаты численного моделирования ( черные сплошные линии )

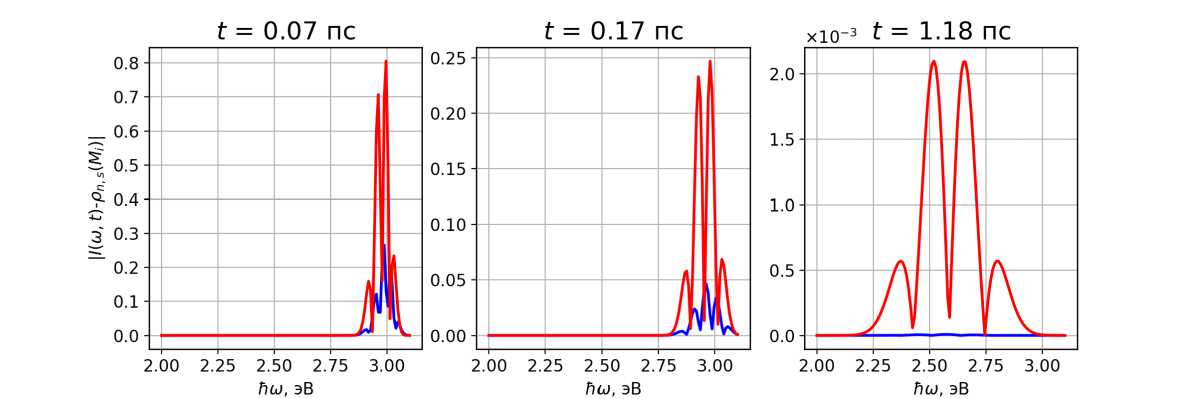
Рис. 6. Абсолютное значение разности между модельным спектром и огибающей плотности вероятности нормального ( красные линии ) и асимметричного нормального ( синие линии ) распределений

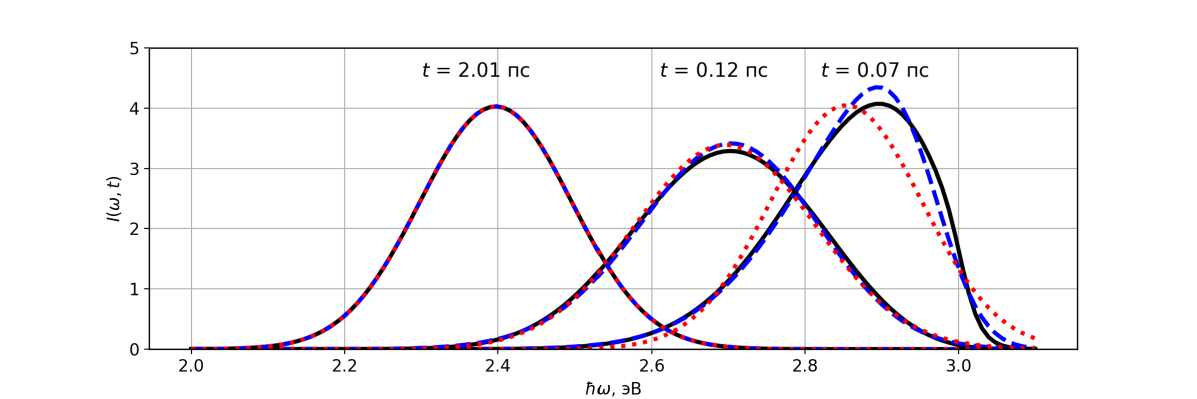
Рис. 7. Наложение нормального ( красные пунктирные линии ) и асимметричного нормального ( синие штриховые линии ) статистических распределений на результаты численного моделирования ( черные сплошные линии ) в случае ярковыраженных колебаний первого момента

На рисунках 5–7 видно, что асимметричное нормальное распределение вполне адекватно воспроизводит форму спектра. Использование же нормального распределения преемлемо только на поздних этапах релаксации, когда асимметрия спектра становится пренебрежимой. Стоит обратить внимание на то, что максимальное несоответствие выбранных распределений провляется на раннем этапе эволюции спектра.

Особенно сильно этот эффект проявляется при высоком вкладе низкочастотной внутримолекулярной колебательной моды (w ₃ = 0 , 4; w ₂ = 0 , 3; w 1 = 0 , 3). Рисунок 7 хорошо показывает этот эффект – форму спектра становится сложнее аппроксимировать простыми распределениями, особенно в ранние периоды релаксации системы. По крайней мере, была проведена проверка на нескольких асимметричных распределениях, для восстановления которых достаточно информации о трех центральных моментах. Возможно, следует обратить внимание на более общие распределения и использовать информацию не только об асимметрии, но и об эксцессе спектра. Также есть резон в построении и изучении свойств производящей функции моментов (moment generating function) – применение к ней обратного двустороннего преобразования Лапласа позволит получить аналитическое выражение для формы исходного распределения. Этот метод находится в разработке и будет рассмотрен авторами в дальнейших работах. С другой стороны, если обратиться к построению исходной модели в работе [8], то можно заметить, что для упрощения результирующего выражения был принят ряд приближений, которые будут нарушаться как раз на ранних этапах релаксации флуорофора и растворителя. Использование же методики, представленной в данном исследовании, даст возможность обойти необходимость введения этих приближений, что и является целью дальнейших изысканий.

Выводы

В данной работе предложен теоретический подход для анализа динамики сольватации фотовозбужденных молекул в полярной среде. Построены выражения для динамики центральных моментов модельного спектра, не требующие использования численных методов. Показано влияние длительностей импульса накачки (лазерное излучение, приводящее систему в возбужденное состояние) и зондирующего сигнала (стробирующее воздействие, позволяющее фиксировать этапы эволюции исследуемой системы) на получаемую динамику спектров флуоресценции. Проиллюстрировано влияние низкочастотной внутримолекулярной колебательной моды на ширину и асимметрию спектра. Предложен способ решения обратной задачи – восстановление динамики и формы спектрального распределения по информации об эволюции моментов. Следующим этапом данного исследования является детальное изучение спектра флуоресценции методами статистического анализа, а также вывод более общих формул моментов спектров для учета внутримолекулярных квантовых мод. Скрипты, использованные для вычислений и построений графиков, доступны в репозитории одного из авторов на платформе github [9].