Динамика тел, погруженных в жидкость

Рассмотрим динамику тел, находящихся в емкости (отсеке), заполненной несжимаемой жидкостью. Будем предполагать, что отсек заполнен полностью, т. е. будем пренебрегать волновыми движениями жидкости. Начнем с более простого случая - одномассовой системы, имеющей одну степень свободы (рис. 1).

Рис. 1. Одномассовая система в отсеке, заполненном несжимаемой жидкостью

Примем следующие обозначения: z(t\ - абсолютное перемещение массы, у(?) - заданное перемещение основания, с - коэффициент жесткости упругой связи.

Дифференциальное уравнение движения тела в жидкости проще всего получить из выражений для кинетической Т и потенциальной П энергий и диссипативной функции Ф, используя уравнение Лагранжа второго рода dt\dqJ Qq 8q где q - обобщенная координата.

Значение кинетической энергии можно представить в виде

27 — Mi2 + ДМм2, или 27 = Л7(м + у)2 + ДМ й2, где u^ = z^-y^ - относительное перемещение массы; М- масса тела; ДМ - присоединенная (приведенная) масса жидкости.

Потенциальная энергия П и диссипативная функция Ф имеют однотипные выражения:

2П - си2, 2Ф = гй2.

Через г обозначен коэффициент сопротивления жидкости движению тела.

Используя уравнение Лагранжа (1) для обобщенной координаты и, получим:

{М + ЛМ^й +гй+си = —М у .                                             (2)

При известных параметрах ускорения у (?) уравнение (2) позволяет определить соответствующие характеристики динамического состояния тела, находящегося в емкости с жидкостью.

Коэффициент сопротивления жидкости движению тела обычно оценивается с помощью ло-сЗ гарифмического декремента колебаний дж по формуле г = ——. Частота собственных колебаний тела в жидкости сож при малом затухании определяется выражением

2 _ С _       ____

^ " М+ДМ -1 + (ДМ^М ’ где и^ = с/М - частота собственных колебаний тела в воздухе.

Приведенная масса жидкости может быть определена по формуле

ДМ = мМ_ж,                                                       (3)

где м - коэффициент приведенной массы; М_ж - масса жидкости, вытесненной телом.

С учетом (3) формуле для квадрата частоты собственных колебаний тела в жидкости можно придать вид

Если влияние границ жидкого объема несущественно, т. е. можно рассматривать колебания тела в безграничном объеме жидкости, то коэффициент присоединенной массы м = 1.

Рассмотрим теперь колебания двухмассовой системы, имеющей две степени свободы (рис. 2).

Введем обозначения: zT и z2 - абсолютные перемещения первой и второй масс; их и м2 -относительные перемещения масс; у - заданное перемещение основания; q, и с2 - коэффициенты жесткости упругих связей; и г2 - коэффициенты сопротивления движению тел; Мх и М2 - массы тел.

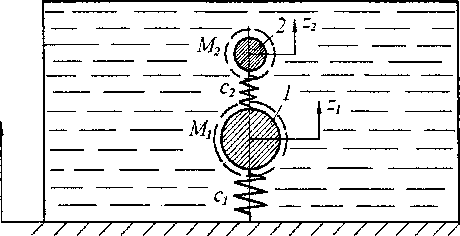
Рис. 2. Двухмассовая система в отсеке, заполненном несжимаемой жидкостью

Учитывая, что и_г = Zj -у, u₂=z₂- z_x, запишем выражение для кинетической энергии системы:

27 = М_х (й] + у)² + ДМ у йу + М₂ (м₂ + й] + уУ + ДМ г (й₂ + “i У, где М, - масса / -го тела; ДМ, - присоединенная масса жидкости i -го тела.

Потенциальная энергия П и диссипативная функция Ф в данном случае имеют вид

277 = Су и/ + с₂ и₂, 2Ф = Гу 2/2 + г₂ й₂.

Используя уравнение Лагранжа (1) для обобщенных координат и_х и и₂, получим:

(Му + ДМ у )й_х + Гу йу + Су и_х -г₂й₂- с₂ м₂ = -М_х у,

(М2 + ДМ^ )(“г + “1) + т2 й2 +с2и2= -МгУ-(5)

Если связь между массами слабая (т. е. с₂ « с_х ), то система этих уравнений распадается на два независимых уравнения:

УМ + ДМ\ )й'1 + г_х й_х + с_х и_х = —М_х у,

• (М2 + ДМ2 )“г + г2 й2 + с2 м2 = -М2 у - (М2 + ДМ2 )йх.

Следовательно, свободные колебания масс, образующих систему, будут происходить независимо одно от другого. Частоты собственных колебаний можно рассчитывать независимо:

и4,ж" м^у^дм^/мУ

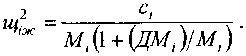
О)

Отсюда можно получить другое условие для разделения уравнений (5): частота собственных колебаний второй массы должна быть намного меньше частоты собственных колебаний первой, т. е. должно быть и^_ж «1Ц_Хж.

Таким образом, в ряде практических случаев можно рассчитывать динамические параметры первой массы независимо от второй, а характеристики колебаний второй массы определять затем, используя в качестве воздействия на нее характеристики движения первой.

Если связь между массами жесткая (с, « с2, или и^ж « и^ж ), то обе массы можно объединить в систему с одной степенью свободы, имеющую жесткость сх , массу М = Мх + М2 и частоту лт(1 + (ж)М)' (8) Уравнение колебаний такой системы имеет вид (2).

Изложенный подход можно применить и к многомассовой системе. Как следует из рассмотренных примеров, уравнения свободных колебаний твердых тел в жидкости отличаются от обычных уравнений колебаний в воздухе только инерционным коэффициентом. Поэтому уравнения свободных колебаний упругих тел в жидкости можно получать любым подходящим методом, добавляя к массе тела присоединенную массу жидкости. Это утверждение справедливо и для балочных упругих конструкций. Так, например, свободные колебания сосредоточенной массы, жестко связанной с консольной невесомой балкой (рис. 3), расположенной в жидкости, описы ваются уравнением

(М + ДМУг + ^-z-O.

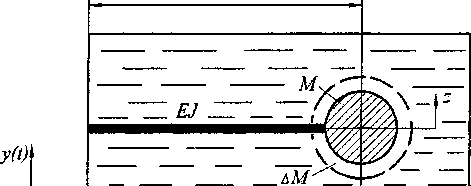
Рис. 3. Консольная невесомая балка с сосредоточенной массой, расположенные в жидкости

Введем в рассмотрение приведенный коэффициент жесткости с„_р

ЗЕЛ

—— и перепишем урав

нение (9) в следующем виде:

^Ма-ДМ^с^-О.

Коэффициент с_пр легко определяется для различных систем методом конечных элементов.

Вынужденные колебания рассматриваемых систем при действии на основание кинематического возбуждения у^ можно получить в относительных координатах, добавляя в правую часть уравнений силу Q = -М у:

• (М + ДМ^й + с_пр и = -М у.                                                  (10)

Рассмотрим изгибные колебания в жидкости балки с погонной массой т(х) и погонной жесткостью ЕЛ(х) (рис. 4). Будем полагать, что известны формы Д_ж(х) и частоты иц^. собственных колебаний балки в жидкости, так что относительные поперечные перемещения балки можно представить в виде суммы

Ограничимся учетом лишь первого тона изгибных колебаний балки. Тогда кинетическая энергия колеблющейся балки будет иметь вид

2Т = Jm(x) [у + /1ж (т) ^ ]2 А + \Дт^ f^ (х) S2 dx, о                                       о где Дт^ - погонная присоединенная масса жидкости.

Рис. 4. Упругая балка с распределенными параметрами, расположенная в жидкости

Потенциальная энергия балки будет определяться выражением

277 = jET^) о

Лж \ / О dx^{2 1}

dx.

Диссипативная функция равна

2Ф = зХж ^EJ^

О

J уж W о dx^{2 1}

dx.

где з_1ж -д_Хж!(рщ_1ж), д_Хж - логарифмический декремент первой формы колебаний упругой

конструкции в жидкости.

Используя уравнение Лагранжа (1) для обобщенной координаты ^(г), получим: ^т„_Р ($1 + з_Хж Щ[_ж 8_Х + мд_ж S))~ ~ ^пр У 1

где тпР = /[^M+^Wl/itW^;

о

(И)

о

«/L =—W^x) ^тпр О

dx2

-12

• dx = —

-        1 +

н/2

/ ид2 = |£j(x) о

У 1ж dx²

о

В случае упругой балки постоянного сечения

2        ^ гг

1 + \Дт) т

где Дт - присоединенная масса жидкости; т_ж - масса жидкости, вытесненной балкой; т - масса балки.

Обозначим через R_x радиус балки. Для круглого длинного цилиндра с l/(2R^>^, совершающего изгибные колебания в безграничном объеме жидкости, л/=1 [1]. При l/(2R^<& значение м в зависимости от //(2^) может быть принято по экспериментальному графику, изображенному на рис. 5 [1].

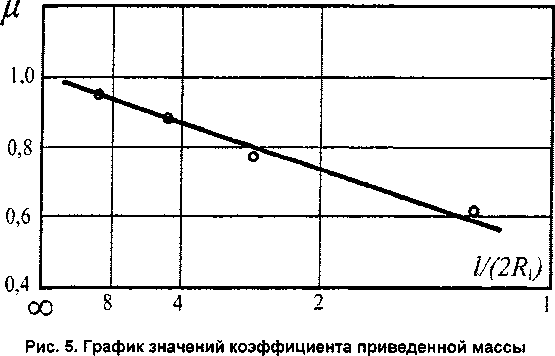
Влияние зазора между стенками полости и балкой большого удлинения l/^2R_x^>% на частоты ее собственных колебаний можно оценить при помощи зависимости коэффициента м от величины отношения радиуса емкости R_o, в которой колеблется балка, к радиусу балки R_x по формуле [1]

м= _{р р} при (1O/R_X <2).

^0/^1

С возрастанием отношения R₀/R_x влияние стенок полости уменьшается, а при R₀/R_x >2 коэффициент ц = 1, т. е. частотные характеристики балки близки к тем, которые имеют место при ее колебаниях в безграничном объеме жидкости.

Рассмотрим на конкретном примере, как влияет жидкость на параметры движения внутренних элементов, находящихся в емкости. Пусть колебания тела в жидкости описываются уравнением

• 7                      1

и + 2й_жм + ^м = -7— _z х У-                                      (14)

(1 + ДМ/М)

Будем полагать, что параметры внешнего кинематического воздействия y(t) заданы в виде спектральной плотности ускорения, которая представляет собой нормальный белый шум с интенсивностью So. Тогда решение уравнения (14) получим в виде [2]:

* 4h, (1+ДМ(мУ

Приближенное значение дисперсии относительного ускорения

Пй =      ----------.

4ИЖ (и дм/м¥

Учитывая, что ж х+дм/м и принимая м = 1, из (15) находим

Щ_о __1______

4^ ^МЖ/МУ’ где ги^ - собственная частота колебаний тела в воздухе.

В случае колебаний тела в воздухе (М_ж = 0) дисперсия относительного ускорения тела будет определяться по формуле

D^S^MV                                (17)

где h₀ - параметр, характеризующий затухание колебаний тела в воздухе.

В частности, для И_ж= Иц из (16) и (17) следует:

^ = 0^M^°'                             (18)

При сделанных допущениях коэффициент К_ж -(1 + Л/_ж/Л/)³ показывает, во сколько раз дисперсия относительного ускорения тела в жидкости меньше дисперсии относительного ускорения тела в воздухе.

При увеличении М_ж (т. е. при увеличении плотности жидкости или увеличении объема тела) дисперсия относительного ускорения тела снижается.