Динамика управляемого движения трехмассового робота по плоской поверхности

Одним из перспективных направлений робототехники являются мобильные роботы, движущиеся за счет периодических колебаний внутренних масс. Работы [1-3] посвящены изучению прямолинейного движения двух- и трехмассовых систем в среде с сопротивлением. Вопросы моделирования криволинейного движения вибрационных роботов по горизонтальной поверхности изучены в [4, 5]. В статье представлены результаты исследования прямолинейного и криволинейного движений робота, перемещающегося за счет периодических колебаний двух внутренних масс. Особое внимание уделено вопросу моделирования взаимодействия корпуса робота с опорной поверхностью.

Описание робота и его математическая модель. Конструкция рассматриваемого робота состоит из 3 основных частей: двух подвижных внутренних масс 1 и 2 и корпуса 3 (рис. 1). Внутренние массы перемещаются относительно корпуса по направляющим 4 . Положим, что корпус контактирует с поверхностью 5 при помощи четырех опорных элементов 6 и движется по ней за счет сил трения.

а                                           б

Рис. 1. а – общий вид робота, б – кинематическая схема устройства:

1, 2 – внутренние массы, 3 – корпус, 4 – направляющие, 5 –поверхность, 6 – опорные элементы, АВ – криволинейная траектория

Введем две системы координат: абсолютную неподвижную систему координат О 1 x 1 y 1 и относительную систему координат Oxy , которая жестко связана с корпусом робота так, что начало координат O совпадает с центром масс корпуса, ось Ox параллельна траекториям движения внутренних масс. Угол φ определяет поворот системы координат Oxy относительно О 1 x 1 y 1 . Будем считать, что корпус робота является абсолютно твердым телом, центр инерции которого расположен в точке О (рис. 1). Внутренние массы 1 и 2 являются точечными и движутся по прямолинейным траекториям, лежащим в плоскости Oxy , параллельны оси Ox и равноудалены относительно центра масс корпуса робота на расстояние b . Законы движения внутренних масс A j ( t ), j =1,2 являются периодическими функциями вида

где x_{C i} - проекция скорости i -ой опоры на ось Ох , M xr , M m , M max — средний, минимальный и максимальный коэффициенты вязкости вдоль оси Ox .

Угол наклона опор относительно оси Oy равен 90⁰, поэтому вдоль нее возникает симметричная сила вязкого сопротивления

Q C =- M_y 0 y CC )

,

Aj (t) = aj sin^y + aj)

где a j – амплитуда, ω j – круговая частота, α j – начальная фаза перемещения внутренней массы.

Робот контактирует с поверхностью в точках C i , i =1, 2, 3, 4, в которых возникают силы сопротивления, при помощи 4 опорных элементов, каждый из которых является абсолютно твердым телом. Опоры могут располагаться под разными углами в вертикальной плоскости относительно оси Ox , что позволяет управлять величиной сил сопротивления. Высота опорного элемента мала, поэтому учитывать ее при определении координат контактных точек C i не будем. Модели сил сопротивления вдоль осей системы координат, связанной с корпусом устройства, определяются углами наклона опор к осям Ox и Oy , а численные значения коэффициентов вязкости вдоль этих осей – углами наклона опор к осям Ox и Oy и свойствами смазывающего вещества. Относительно положительного направления оси Ох i -ый опорный элемент может быть ориентирован под тремя углами γ i , каждому из которых соответствует своя сила вязкости

где M _{y 0} — коэффициент вязкости вдоль оси Оу , (0)

y_Ci – проекция скорости i -ой опоры на ось Оу .

Зависимость коэффициентов вязкости от свойств смазывающего вещества проявляется в изменении численных значений параметров sr min max

M _x о , M _x о , M _x о , ^M y 0 при использовании различных веществ по следующей формуле:

Mx0i = My0 (1+ p.x)

,

где 0≤χ≤1 – коэффициент, зависящий от свойств смазывающего вещества, а

Pi =

Г 1

145 yi

- 2 sgn(xC0))

параметр, являющийся функцией угла наклона опоры к положительному направлению оси Ox (рис. 2).

Q x 0          sr (0)

c i = - ^M о ^xa при Y i =90 0 , ' 0, x (0) = 0,

Ci

Qx0 = J-mminx,x(0) > 0,

C_i               x 0     C_i , C_i         ,

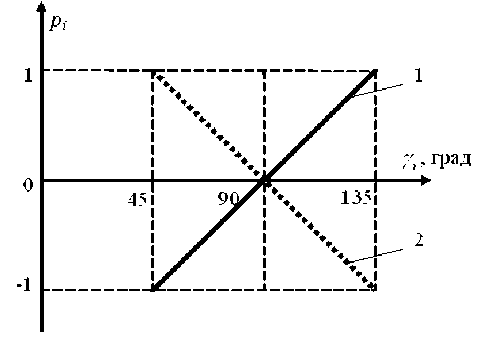
Рис. 2. График зависимости p i ( Y i ): 1 - x ⁽⁰⁾ >  0 ,

Ci

M max x (⁰⁾ x 0     C_i

(0) C i

0, x (0) = 0, Ci

_QC x_i 0

= <

max (0)     (0)

^M x 0 x C i , ^xC,

при γ i =45⁰,

> 0,

M min x (⁰⁾ x 0     C_i

x(0) < 0

Ci

2 - x (⁰⁾ <  0 C_i

Структурная схема системы управления роботом изображена на рис. 3.

при γ i =135⁰, (4)

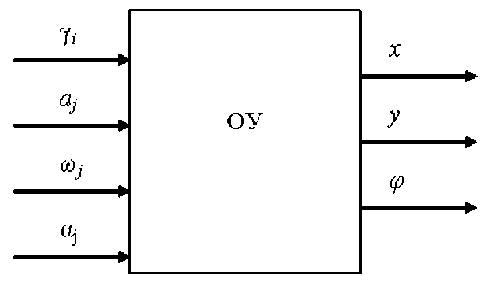
Рис. 3. Структурная схема системы управления роботом

В качестве управляющих воздействий выступают: γ i – угол наклона i -ого опорного элемента в вертикальной плоскости относительно продольной оси корпуса, а j , ω j , α j – амплитуда, круговая частота и начальная фаза движения j -ой внутренней массы. Управляемыми параметрами являются координаты х и у центра масс корпуса устройства и угол φ поворота корпуса робота относительно его центра масс. Дифференциальные уравнения движения объекта имеют вид:

mx + E m [ x - 2<& >A. sin ф - <&& ( A. sin ф + B cos ^ ) - j = 1

• <              j = 1

• -    & ² ( A j sin ф + B j cos ф ) + A j. sin ф ] = Q y i ,

J< & ■ E m j [ - sin ф ( xA j + yB j ) - cos ф ( xB j - yA j ) + ^j = 1

+ 2 < & A j A j + <& (.A j + B ²) - A j B j ] = M o .

где Bj = (- 1)j b - координата j-ой массы в проекции на ось Оу,

• -    M y 0 sin ф ( 5c sin ф - y cos ф - & kk i )),

Q y i = ]L (-M x o i sin Ф ( x cos ф + y sin ф - & d) ) + = 1

• +    M y ₀ cos ф ( xc sin ф - y cos ф - &kci )).

• -    проекции главного вектора сил сопротивления на оси О 1 х 1 и О 1 у 1 ,

• -    главный момент сил сопротивления,

• -    момент инерции корпуса J .

^M o =^ E ^{[ -} M x o i ^d i ⁽ xC ^cos Ф ^{+ y sin} Ф ^- &d i ⁾⁺ M y o ^k i ⁽ x ^sin Ф ^{- y c}oS ф ^- &k^{k )]}        (11)

Исследование характера движения робота. Результаты численного моделирования позволяют выявить характер перемещения объекта в зависимости от параметров модели силы вязкого сопротивления, обусловленной положением опорных элементов, а также параметров закона движения внутренних масс. Установлено, что при синфазном движении внутренних масс и одинаковой ориентации опор γ = γ i относительно вертикали объект совершает колебательные движения вдоль оси, совпадающей с продольной осью корпуса, при симметричной модели силы вязкого трения, или перемещается вдоль той же оси в сторону меньшего коэффициента вязкости при асимметричной силе сопротивления (рис. 4).

При том же законе колебаний внутренних масс и разных углах наклона опорных элементов корпус робота поворачивается относительно его центра масс, который совершает колебания вдоль двух осей абсолютной системы координат (рис. 5).

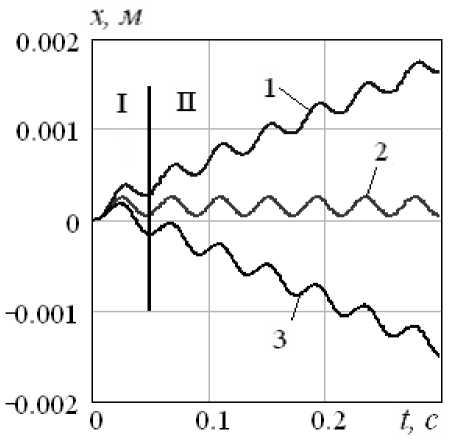
Рис. 4. Графики движения робота при синфазном перемещении внутренних масс: 1 – γ =45⁰, 2 – γ =90⁰, 3 – γ =135⁰, I – переходный режим, II – установившийся режим

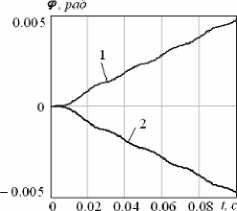
а                                    б

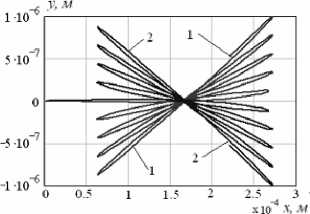
Рис. 5. Графики: а – φ ( t ), б – y ( x ) при синфазном перемещении внутренних масс: 1 – γ 1,3 =135⁰, γ 2,4 =45⁰, 2 – γ 1,3 =45⁰, γ 2,4 =135⁰

При движении внутренних масс в противофазе и симметричной силе трения происходит перемещение устройства по одной обобщенной координате – углу поворота (рис. 6). Введение асимметричной силы сопротивления при γ = γ i приводит к возбуждению движения по трем обобщенным координатам (рис. 6, 7).

При разной ориентации опор и противофазных колебаниях внутренних масс робот совершает вращательное движение относительно неподвижного центра масс корпуса (рис. 8).

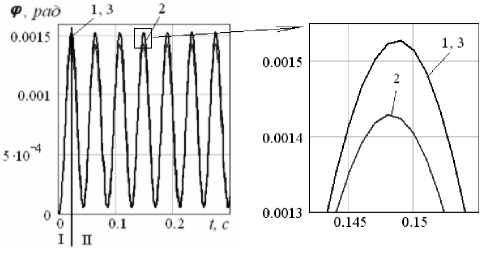
Рис. 6. Графики угла поворота корпуса робота при перемещении внутренних масс в противофазе: 1 – γ =45⁰, 2 – γ =90⁰, 3 – γ =135⁰, I – переходный режим, II – установившийся режим

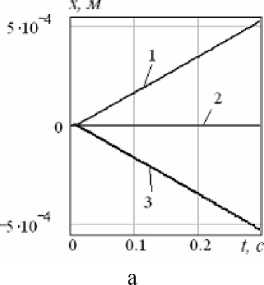
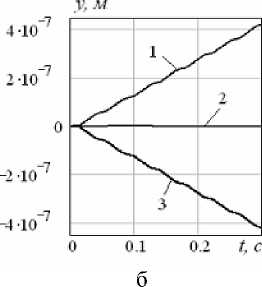
Рис. 7. Графики а – x ( t ), б – y ( t ) при перемещении внутренних масс в противофазе: 1 – γ =45⁰, 2 – γ =90⁰, 3 – γ =135⁰

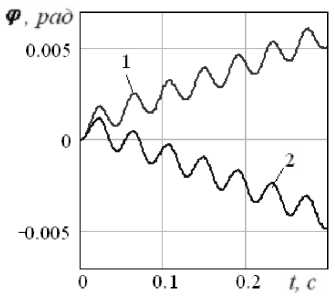
Рис. 8. Графики движения робота при перемещении внутренних масс в противофазе: 1 – γ 1,3 =135⁰, γ 2,4 =45⁰, 2 – γ 1,3 =45⁰, γ 2,4 =135⁰

Программно-управляемое движение робота. По результатам исследования характера движения робота можно сделать вывод о том, что прямолинейное движение устройства с ненулевой средней скоростью происходит при синфазном движении внутренних масс при одинаковой ориентации опорных элементов γ=450, 1350, поворот робота относительно неподвижного центра масс корпуса осуществляется при разных углах наклона опор γ1,3=1350, γ2,4=450 или γ1,3=450, γ2,4=1350, если внутренние массы колеблются в противофазе. В соответствии с этим предложен алгоритм ступенчатого перемещения объекта, реализуемый путем чередования участков прямолинейного и вращательного движений. Варьируя время прямолинейных участков и значения углов поворота корпуса, можно реализовать движение робота по различным криволинейным траекториям (рис. 9).

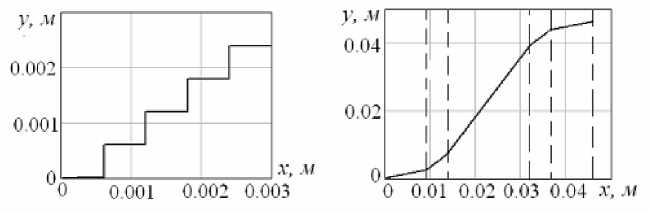
а                                   б

Рис. 9. Криволинейное движение виброробота: а – ступенчатое, б – по s-образной траектории

Выводы: в работе исследована динамика управляемого движения трехмассового мо- ₁ бильного робота, перемещающегося по гори-   ^.

зонтальной плоскости в среде с вязким сопротивлением при движении двух внутренних масс. Установлено влияние модели силы вяз- ^2. кого сопротивления, ориентации опорных элементов и параметров законов колебаний внут- 3. ренних масс на характер движения робота. Реализовано программно-управляемое движение устройства по криволинейной траектории, заключающееся в чередовании прямолинейно- 4. го и вращательного перемещений корпуса за счет управления сдвигом фаз колебаний двух внутренних масс и углами наклона опорных _5. элементов.