Динамика заряженной частицы в поле вращающегося намагниченного небесного тела

Движение заряженных частиц в магнитном поле небесного тела, магнитная ось которого совпадает с осью вращения, хорошо изучено на примере магнитного поля Земли. Это, так называемая, задача Штермера. Известно, что в таком магнитном поле существуют замкнутые области пространства, в пределах которых движутся заряженные частицы с энергией, не превышающей некоторого определенного значения. Такие области получили название радиационных поясов [1,2].

В 1907 году Карл Штермер, исследуя движение заряженных частиц в дипольном магнитном поле, показал, что помимо полной энергии частицы, азимутальная компонента обобщенного импульса движущейся частицы, также является интегралом движения. Сохранение этих двух физических величин обусловлено независимостью от времени магнитного поля и цилиндрической симметрией относительно оси магнитного диполя. Наличие двух интегралов движения дает возможность исключить из уравнений движения одну координату и ввести двумерную эффективную потенциальную энергию. В работах [3,4] этот метод использован для аналитического и численного исследования траекторий заряженных частиц в магнитном поле Земли.

Между тем, существуют тела, магнитная ось которых наклонена относительно оси вращения. Вопрос существования радиационных поясов в окрестности таких тел изучен в работах [5,6]. Наиболее известным примером таких тел являются нейтронные звезды. Часть из них, а именно пульсары, интенсивно исследуются с использованием наблюдаемого излучения. Динамика заряженных частиц в поле нейтронной звезды имеет важное значение для объяснения природы излучения пульсара. Аналитическое решение уравнений движения в магнитном поле с наклонной магнитной осью представляет определенные трудности в связи с тем, что поле не обладает аксиальной симметрией и момент импульса частицы не является интегралом движения. В связи с этим, все предыдущие работы, посвященные динамике заряженных частиц в магнитосфере тел с наклонной магнитной осью, представляют собой либо численное интегрирование уравнений движения, либо приближенные оценки характера движения частиц. В настоящей статье излагается метод, который позволяет определить разрешенные и запрещенные для движения частиц области пространства в поле наклонного магнитного ротатора, если это поле аппроксимировать полем диполя.

Электромагнитное поле вращающегося намагниченного тела существенно зависит от того, является оно проводящим или нет. В случае проводящего небесного тела на его поверхности индуцируется распределенный заряд, создающий собственное квадрупольное поле. Предполагается, что нейтронные звезды являются проводящими с очень низким коэффициентом сопротивления. Первая модель электрического поля, которое генерируются в окрестности нейтронной звезды была разработана Дойчем [7]. Ряд других моделей были предложены и изучены несколькими авторами. Обзор этих работ можно найти в монографии [8].

Также существуют небесные тела, состоящие из непроводящего вещества, которые вращаются вокруг оси, не совпадающей с осью магнитного поля. Их магнитное поле хорошо аппроксимируется полем прецессирующего магнитного момента или «наклонным ротатором» [9]. Электромагнитное поле и магнитосфера наклонного проводящего ротатора изучались многими авторами. См., например, [10-15]. В работе [15], кроме того, проведена оценка энергии, которая может быть приобретена частицами в процессе ускорения в магнитосфере.

Некоторые вопросы динамики заряженной частицы в электромагнитном поле в вакууме были рассмотрены в статьях [16,17]. Задача Штермера для параллельного проводящего ротатора была исследована в работе [18]. Обобщенная задача Штермера с учетом электромагнитных и гравитационных сил, действующих на заряженные пылинки вблизи планеты, рассмотрена в статье [20]. Динамика заряженной частицы вблизи бессиловой поверхности вращающейся намагниченной сферы была детально исследована в [21,22].

В настоящей работе использован метод исследования динамики заряженных частиц с помощью эффективной потенциальной энергии разработанный в [5,6]. Метод основан на использовании интеграла движения для полной энергии во вращающейся системе отсчета. Такой подход, в частности, позволяет определить условия при которых в окрестности намагниченного небесного тела с наклонной магнитной осью существуют замкнутые области пространства, в которые могут захватываться частицы, и позволяет исследовать геометрию таких областей.

1.    Электромагнитное поле вращающейся намагниченной сферы

Первой моделью, описывающей магнитосферу нейтронной звезды является вакуумная модель [23,24]. Deutsch [7] моделировал нерелятивистскую вращающуюся намагниченную звезду как идеально проводящую сферу, жестко вращающуюся в вакууме. Для того чтобы ввести релятивистскую модель источника поля Belinsky и др. [25,26] рассмотрели бесконечно тонкий постоянный магнит конечной длины. Эта модель является применимой для расчета поля на больших расстояниях, но она не может быть использована для расчетов в ближней зоне, поскольку геометрия источника существенно отличается от сферической.

Georgiou [27] нашел точные релятивистские решения для электромагнитного поля внутри и вне вращающейся намагниченной нейтронной звезды. Расчет поля был сделан как обобщение поля медленно вращающейся нейтронной звезды, которая была изучена в [28], с учетом эффектов общей теории относительности. Поле вращающейся намагниченной сферы не являющейся ни проводником ни диэлектриком было вычислено в работе [29]. Существует большое разнообразие других работ, в которых представлены расчеты электромагнитного поля вращающейся намагниченной сферы [30-32]. Эти результаты существенно зависят от используемой модели намагниченной сферы и скорости ее вращения.

Модель релятивистской вращающейся сферы достаточно сложна. Прежде всего, твердый шар не совместим с теорией относительности. Следовательно, релятивистской моделью может быть жидкая или газовая модель. Во-вторых, поле быстро вращающегося тела зависит от формы тела (которая, вообще говоря, уже не является сферической) и от природы намагниченности. В этой статье мы принимаем в качестве модели внешнего электромагнитного поля поле нерелятивистской вращающейся однородно намагниченной проводящей сферы. А именно, считаем что скорость точек экватора этой сферы много меньше скорости света. Если ввести приведенный радиус сферы a = зто/c где? ® — угловая скорость врашеиия. r° — радиус с ( } ) еры. a c — скорость света, то указатшое условие запишется как a 《 1. Цилиндр радиуса R = c/з принято называть световым цилиндром. В этих терминах нерелятивистской вращающейся сферой является сфера, радиус которой много меньше радиуса светового цилиндра.

Исследование взаимодействия заряженной частицы с полем намагниченной сферы мы проводим в два этапа. В следующих разделах мы пренебрегаем размерами сферы, то есть, считаем, что частица находится на расстояниях, много больших радиуса сферы. Нетрудно показать, что все модели в цитированных выше работах дают одно и то же представление для поля вдали от поверхности вращающегося тела, какую бы форму оно не имело, — это поле совпадает с полем точечного прецессирующего диполя. В разделе 4 мы исследуем особенности взаимодействия частиц с полем вблизи поверхности сферы, используя формулы Дойча в приближении нерелятивистской сферы.

Разложим выражения, полученные Дойчем [7] по степеням a. С точностью до второго порядка по a мы получаем следутошпе уравнения для векторов электрического E ii магнитного H поля в сферической системе координат г, Ө, ^ [6]:

Er

μk3a2 ^р^

{ cos а(3 cos 2Ө + 1)+ р sin а sin 2Ө[3С(р, А) — р cos А] } ,

Eθ

— [рС (р, А) sin а (1 — a2 cos 2Ө ) + 、 cos а sin 2ө],

(1.1)

E^ = ^-5(р, А) sin а cos Ө (1 —      ,

2 〃 k³

Hr =———[cos а cos Ө + С(р, А)р sin а sin Ө], ρ³

μk3

(1.2)

Нө = —з~ [cos а sin Ө + Ср(р, А)р2 sin а cos Ө],

Нф =—— sin аSp(р, А), ρ где1 儿—магіштііып мом(?ит с(})(?ры. а — угол мс'жду вектором магнитного момента，口 осыо враш.еипя. А = g — st, р = r®/c, k = ®/c. Ось Z направлена вдоль вектора угловой скорости з. Мы также разложили:

sin(А — a) 仁 sin А — a cos А, cos(А — a) 仁 cos А + a sin А.

Здесь введены функции

S(р, А) = ^sin(р + ^А) — cos(р + А), С (р, А) = ^{cos(р + А)} + sin(р + А),           (1.3)

ρρ обладающие следующими свойствами (аргументы опущены):

S² + С² = 1 + р^-2, S sin А + С cos А = р^-1, С sin А — S cos А = 1,            (1.4 )

∂S дА =С,

др 三 Sp = sin(р + А) +

cos(р + А)   sin(р + А)

ρ            ρ2

∂C ∂λ

— S,

дС                     sin(р + А)

丽 三 Ср = cos(р + А)-- 拳~-

cos(р + А) ρ2

(1.5)

(1.6)

Поле, описываемое формулами (1.2), является полем вращающегося точечного магнитного диполя, в то время как электрическое поле (1.1) является суперпозицией дипольного и квадрупольного полей. Квадрупольная часть состоит из членов, пропорциональных a²/р² и убывающих с расстоянием как р^-4. На больших расстояниях р 》 a эта часть стремится к нулю быстрее и электромагнитное поле становиться полем вращающегося магнитного диполя.

Поле вблизи поверхности намагниченного тела существенно зависит от используемой модели. Поле (1.1) найдено для идеально проводящей сферы. Поле наклонного ротатора с использованием других моделей найдено в работах, цитированных выше, и сильно отличается от поля, полученного в [7]. Но если разложить поле, полученное в различных моделях по степеням a, то вдали от поверхности оно принимает форму поля вращающегося точечного диполя. Например, это имеет место для полей в моделях, принятых в работах [33] и [29]. Внешнее поле однородно намагниченной не проводящей сферы также совпадает с полем точечного диполя.

Далее рассмотрим динамику заряженных частиц в поле точечного магнитного диполя. Эта модель применима вдали от поверхности тел, имеющих существенную дипольную компоненту магнитного поля, и во всем пространстве вне не проводящей намагниченной сферы Тогда магнитное поле дается уравнениями (1.2), а электрическое поле имеет вид

Er = 0,

Еө = — ^―С(р, А) sin а,  E^ = ^―S(р, А) sin а cos Ө.

(1.7)

ρρ

Поле (1.2) и (1.7) может быть представлено с помощью четырехмерного векторного потенциала

AJ В с ( 1 )( ?рпч ( ?скоп системе координат x^v = (ct,r,0,g) его можно представить в виде

A0 = A¹ = 0,  A² = —与 S(p, A) sin a,

A3

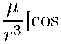
а — C(p, Х)р sin а ctg Ө].

(1-8)

В следующих разделах мы изучим динамику и потенциальную энергию заряженных частиц в поле вращающегося диполя, которое задается уравнениями (1.2) и (1.7), а в разделе 4 вернемся к полю, заданному уравнениями (1.1), (1.2).

2.    Эффективная потенциальная энергия

В работах [5, 6] показано, что в поле наклонного магнитного ротатора существуют области захвата заряженных частиц с энергией ниже определенных значений. Здесь мы найдем эти области другим методом. Для определения разрешенных для движения частицы областей обычно используется метод эффективной потенциальной энергии. Метод состоит в том, что полная энергия частицы представляется как сумма положительно определенной квадратичной комбинации обобщенных скоростей (эффективная кинетическая энергия) и некоторой функции обобщенных координат (эффективная потенциальная энергия). Разрешенные области определяются из условия, что полная энергия больше эффективной потенциальной энергии. Наличие интегралов движения позволяет исключить соответствующее число обобщенных скоростей и сузить допустимую область движения.

Пусть произвольное электромагнитное поле, вращающееся с угловой скоростью ®, задано потенциалом

Av = Av(r, Ө, ф — ®t + p).

В сопутствующей, вращающейся системе отсчета x^v = (ct, r, Ө, ^), ^ = 夕 —st поле не зависит от времени. Следовательно, соответствующий обобщенный импульс

e

(2.1)

po, = mu。，+ -A。， c сохраняется. Штрихами обозначены величины во вращающейся системе отсчета, uv = (ct,Г,Ө,j)— четырехмерная скорость. Точкой обозначена производная по собственному времени. Временная компонента 4-импульса po, представляет собой энергию частицы в сопутствующей системе отсчета деленную на скорость света.

Чтобы ввести эффективную потенциальную энергию во вращающейся системе отсчета, достаточно найти уравнение, содержащее сумму квадратов компонентов скорости, интеграл движения и потенциал как функцию координат. Например, можно использовать, равенство g»v，u『uv，= c2,

(2-2)

rje g/ J — метрііч(?скпп тензор врашатошепся сіістемн отсчета g/v，=

/1 — p2 sin2 Ө	0	0	— rp sin2 Ө
0	— 1	0	0
0	0	- r2	0
— rp sin2 Ө	0	0	— r2 sin2 Ө.

(2.3)

Подставим в (2.1) и 。 ，

п，                     ， uo, = go,o, u  + go,3, u

/ ii выразіш u0

u⁰ ，

mgo,o ，

Подставляем это выражение в тождество (2.2)

—(po, — g0,3, u³,

e

— Ao,) c

c² = ^{(p o} , ^— c ^{A o ， )} 2 + gi,i, (u¹, )2 + g2,2, (u² ， )² + ^{g o , o ， g 3 , 3 ， — g} 2 ， 3 , (u3, )2 m²go,o ，         '                  '                           go,o ，

(2-4)

(P0」彳A。？、- c2 = * + r2 Ө? +  r2 б Ө @ m2(1 — p2 sin2 Ө)                      1 — p2 sin2 Ө

Разрешенные для движения области определяются неравенством

( Ро , — eAo^z)2 > m²c²(1 — р² sin² Ө).

c

Поверхность, ограничивающая разрешенную область, задается уравнением

(po , — eAo^z )2 = m²c²(1 — р² sin² Ө). c

⑵ 5)

(2.6)

Если ввести безразмерную полную энергию частицы E = po ， /mc, то уравнение поверхности, разделяющей разрешенную и запрещенную для движения области, примет вид

( e- Та 。) ² = 1

mc2

— р² sin² Ө.

⑵ 7)

Семейство поверхностей, задаваемых параметром E, можно представить как эквипотенциальные поверхности потенциала

V

± \/1 - р² sin² Ө +--— Ao^z.

⑵ 8)

mc2

Первое слагаемое, не зависящее от электромагнитного взаимодействия, можно интерпретировать как «потенциал» центробежной силы во вращающейся системе отсчета. Действительно, его положительное значение можно записать в виде

/  GR

"V1-， где1 R = r sin Ө — расстояние от осп вратпетшя. В о сстаі i авлив ая размерность п переходя к пере ля-тивистскому приближению ®R《c, запишем mc2VCf = mc2 — 2 mJR2.

Градиент этого выражения с обратным знаком дает нерелятивистскую формулу для центробежной силы F = m^²R. Отстода. в вастностн сттепуе 匸 "что первое слагаемое в (формуле (2.10) должно быть взято с плюсом. Таким образом, эффективная потенциальная энергия заряженной частицы в произвольном электромагнитном поле, созданном вращающимся с постоянной скоростью источником поля, равна

V

J1 - р² sin² Ө +-- 2 A 。， .

⑵ 9)

Найдем эффективную потенциальную энергию прецессирующего дипольного момента. Для этого с помощью матрицы преобразования

/10 0 ®/с 、

V _ ^х^ _ 0 100

Jw = дХ^7 =0010

\0 0 01 преобразуем потенциал поля (1.8) в сопутствующую систему отсчета:

Ао ， = ^— [C (р, 明 Р sin 2Ө sin а — 2 sin² Ө cos а], 2rc

Аі , =0,

А2 ， = 〃 S(p,3)sin а,

Аз ， = — [C(р, ^)рsin 2Ө sin а — 2 sin² Өcos а]. r

(2.10)

(2.11)

(2.12)

(2.13)

(2.14)

Подставляя в (2.9), получим

V = Ji - p² sin² Ө +    [C (р, 3)Р sin a sin 2Ө - 2 cos a sin² Ө] , N = e 〃： .

⑵ 15)

2ρ                                      mc

Эта формула совпадает с выражением, полученным в работе [6] другим методом. Заметим, что все физические параметры частицы и поля собраны в одном безразмерном параметре N. Например, для электронов значение |N| для пульсара в Крабовидиой туманности составляет 5 • 1010, для 1(.)пптера - 0.03- для Земли — 3 • 10-7.

Для удобства аналитического исследования удобно исключить переменную р из аргумента тригонометрических функций в C(р, 3) в формуле (2.15). Для этого сделаем замену 3 = П — Р + о, где sin σ

ρ

71+7

cos σ

1+ρ2.

⑵ 16)

В таком представлении потенциальная энергия становится симметричной относительно плоскости

П = 0, п проходяшеп qepe ： 3 векторы 从口 и ：

V = J1 — р² sin² Ө + ^ ( 71+~Р2 sin a sin 2Ө cos п — 2 cos a sin² Ө ) .

(2.17)

Кроме того, функция V симметрична относительно преобразований п т П + п; Ө т п — Ө.

На рисунках ниже представлены примеры сечения эквипотенциальных поверхностей плоско-стыо п = 0- проходяшеп qepe：3 ось врашеипя небесного тела, для положительно п отрптіателыю заряженных частиц. Эквипотенциальные поверхности определяются уравнением V = const. Это означает, что частица, обладающая полной энергии E и имеющая нулевую скорость на эквипотенциальной поверхности V = E/mc2, может двигаться согласно уравнениям движения в области, где потенциальная энергия меньше ее полной энергии. Например, положительно заряженная частица с полной энергией E = 1.08 mc2 может двигаться везде, кроме замкнутой области, имеющей форму гантели, отмеченной значением 1.08 на рисунке

1 .

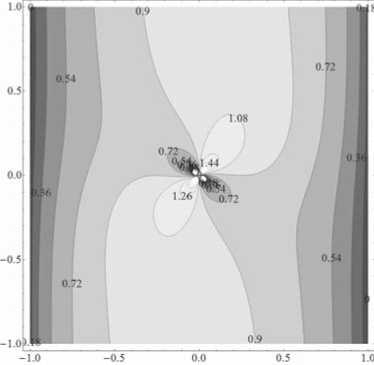
Рис. 1. Сечения эквипотенциальных поверхностей для N = 0.1, п = 00, a = 800.

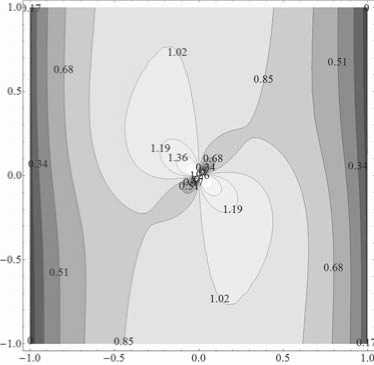
Рис. 2. Сечения эквипотенциальных поверхностей для N = -0.1,п = 00,a = 800.

Здесь и далее представлена структура потенциальной энергии для a < п/2, для положительно и отрицательно заряженных частиц. Структура для a > п/2 может быть получеиа заменой e на —e ii Ө на п — Ө.

На рисунках 1 и 2 изображены профили для N = ±0.1, а на рис. 3 и 4 — для N = ±10. Знак N совпадает со знаком заряженной частицы согласно определешпо N (2.15). Как видно из рисунков 1, 3 потенциальная энергия положительно заряженной частицы имеет потенциальную долину в виде тора вокруг центра поля. Для частиц с относительно малой энергией существует две разрешенные области. Одна из них - это замкнутая область внутри тора и другая область

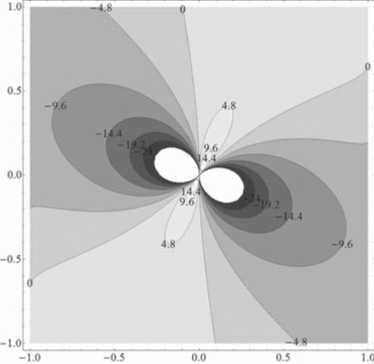
Рис. 3. Сечения эквипотенциальных поверхностей для N = 10, п = 00,а = 450.

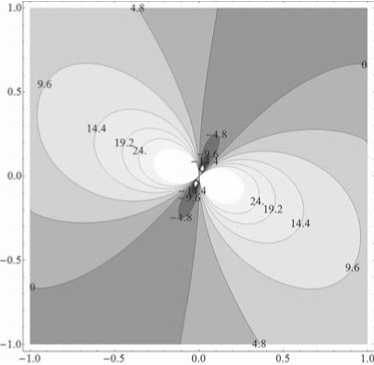
Рис. 4. Сечения эквипотенциальных поверхностей для N = -10, п = 00,а = 450.

вне искривленной цилиндрической поверхности. Например, на рис. 1 это соответствует частицам с энергией меньше чем E = 0.72. Сравнивая рисунки 1, 2 и 3, 4, видим, что изменение знака заряда приводит к тому, что «потенциальные холмы» сменяются «потенциальными ямами» и наоборот.

3.    Стационарные точки эффективной потенциальной энергии

В стационарных точках эффективной потенциальной энергии частица может находиться в состоянии равновесия —— устойчивого, неустойчивого или безразличного в зависимости от вторых производных. Вопрос наличия экстремумов потенциальной энергии чрезвычайно важен для анализа процесса формирования магнитосферы небесного тела — в случае существования минимумов потенциальной энергии заряженные частицы могут накапливаться в окрестности этих минимумов. В работе [6] показано, что потенциал (2.15) имеет 6 стационарных точек — 2 точки в экваториальной плоскости и 4 точки вне этой плоскости. Система уравнений на координаты стационарных точек имеет вид

∂V

dqi

0,

(3.1)

rj,e qi = р, Ө, ^. Если | N | 《 1. то координаты всех статіііоііарпых точек pi много меньше едпшшы. Тогда систему уравнений (3.1) можно разложить по ри представить решение в аналитическом виде [5].

Для положительно заряженной частицы:

р1 = ； 卜。 s а + ， 9 - sin² а ]

р2 = ； 卜。 s а + а/9 - sin² а ]

tg Ө1 = ₉ .1

2sinα tgθ2 =   1

2sinα

[3 cos а + а/ 9 — sin² а [3 cos а + а/ 9 — sin² а

ψ1 =0,

ψ2 = π.

Для отрицательно заряженной частицы:

р3 = N 卜 р4 = N 卜

cos а —

cos а —

， 9 - sin² а],

， 9 - sin² а],

tg θ3

tg θ4

2sinα

2sinα

3 cos а — а/ 9 — sin² а

卜

3 cos а — а/ 9 — sin² а

ψ3 =0,

ψ4 = π.

И в экваториальной плоскости две симметричные стационарные точки

Р5,6 = (N cos а)^1/3, 现 =2, 现

(3.2)

(3.3)

(3.4)

(3.5)

(3.6)

существующие при условии, что N cos а > 0. Это означает, что две последние стационарные точки соответствуют положительным зарядам, если угол между вектором угловой скорости и магнитным мом ( ?итом 从 острый ii отршіателыіым ^зарядам ( ?сли этот угол тупой.

Если |N| не мало, то в апалігтичсч?коп 巾 орме удается выразить только а'зимутальпые координаты стационарных точек. Нетрудно убедиться в том, что стационарные точки при Ө = п/2 лежат в плоскости п = 0, п, а в экваториальной плоскости они имеют азимутальные координаты П = п/2, 3n/2.

Все стационарные точки являются седловыми точками эффективной потенциальной энергии, то есть, они соответствуют положениям неустойчивого равновесия заряженной частицы во вращающейся системе отсчета. В случае | N |《 1 это утверждение доказано аналитически [5]. Если | N | не мало, то это видно из графического представления поверхностей уровня потенциальной энергии. В частности, на рис. 5 и 6 представлены сечения эквипотенциальных поверхностей, построенных по формуле (2.17) для положительно и отрицательно заряженных частиц, соответственно, при | N | = 0.5. '

Рис. 5. Сечения эквипотенциальных поверхностей для N = 0.5, п = 00, а = 600.

Рис. 6. Сечения эквипотенциальных поверхностей для N = - 0.5, п = 00, а = 600.

На рис. 5 седловые точки находятся в точках соприкосновения двух эквипотенциальных поверхностей с уровнем энергии V 心 0.2287. а на рис. 6 — поверхностей, соответствующих уровню V 心 0.6789. С ростом в ( ?лпчііііы магнитного мом ( ?ита ііебестюго те, 「 а ， статіііоііарные точки уда.-ляются от оси вращения асимптотически приближаясь к поверхности светового цилиндра.

4.    Потенциальная энергия вблизи проводящей однородно намагниченной сферы

До этого мы пренебрегали квадрупольным электрическим полем, которое генерируется индуцированными зарядами в случае проводящего небесного тела. Поэтому полученные результаты справедливы для поля непроводящего тела или для поля проводящего тела, но на расстояниях, больших по сравнению с размерами небесного тела, поскольку квадрупольное поле убывает обратно пропорционально четвертой степени расстояния. Как уже упоминалось в разделе 1, электрическое поле вблизи звезды зависит от используемой модели. В этом разделе мы исследуем потенциальную энергию заряженных частиц в поле абсолютно проводящей намагниченной сферы [7]. Эти поля описываются уравнениями (1.1) и (1.2). Соответствующий четырехмерный векторный потенциал может быть записан как:

A0 = — :r ⁰ : [3pC(p, A) sin 2Ө sin a + cos a(3 cos 2Ө + 1)], 6cr³

A1 =0,

A² = —与 S(p,A) sin a,

(4.1)

μ

A³ = —----- [cos a sin Ө — C(p, A)p sin a cos Ө].

r3 sin θ

Преобразуем этот потенциал во вращающуюся систему отсчета и подставим его в уравнение (2.9). В результате получим потенциальную энергию с учетом квадрупольного электрического поля

V

J1 — p² sin² Ө + —

2ρ

{[ C (p, 明 p sin a sin 2Ө — 2 cos a sin² Ө]

(1 - 02)-

4 a2

cos α 3 ρ2 cos α

.

(4.2)

Она отличается от потенциальной энергии (2.15) членами, пропорциональными a²/p², г де a = зто/c Величина a для реальных небесных объектов значительно меньше единицы. Для примера, величина a для Земли. 1(.)пптера и пульсара в Крабовидиой туманности равна ： 1.5 • 10-6. 4 • 10^-5 ii 7.6 • 10-3. Представим примеры < ) квііпотеішііалыіых поверхностей для a = 0, 01. Гра ( 1 ) пки. построенные для всего интервала р внутри светового цилиндра, практически не отличаются от представленных в разделе 2. Отличие наблюдается лишь в области р 〜 a. Эти различия видны на рисунках 7- 10.

Отличительным свойством потенциальной энергии в этом случае является то, что для малых углов наклона а, для отрицательно заряженных частиц, не существует замкнутых областей захвата. Для больших углов наклона, близких к 900, существует минимум потенциальной энергии для отрицательных и положительных заряженных частиц. Эти минимумы и области захвата отделены от поверхности сферы как видно из рисунков 9 и 10. Форма сечений в пределах области р 〜 a не меняется с ростом N. Причина в том, что первый член в уравнении (4.2) близок к единице в случае малых р ii им можно пренебречь, поскольку потенциальная 'Энергия определена с точность то до аддитивной константы.

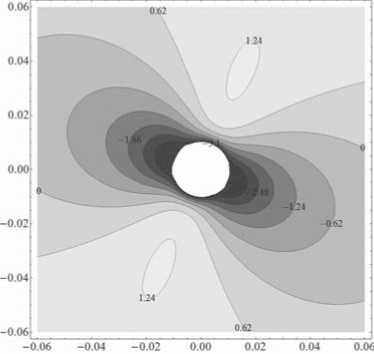
Рис. 7. Сечения эквипотенциальных поверхностей для N = 0.1, п = 00, a = 450.

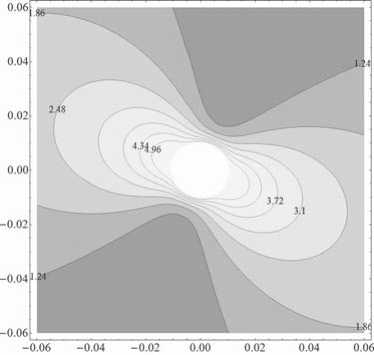
Рис. 8. Сечения эквипотенциальных поверхностей для N = -0.1,п = 00,a = 450.

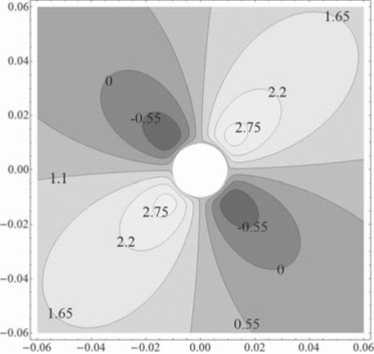
Рис. 9. Сечения эквипотенциальных поверхностей для N = 0.1, п = 00, a = 900.

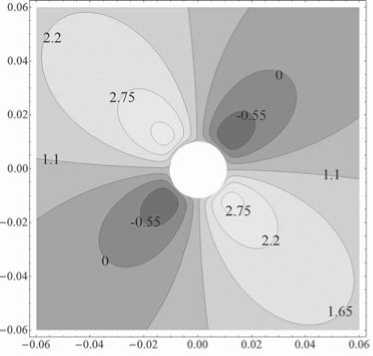
Рис. 10. Сечения эквипотенциальных поверхностей для N = -0.1,п = 00,a = 900.

Заключение

Для того, чтобы выяснить, возможны ли «радиационные пояса» в окрестности небесного тела с наклонной магнитной осью, исследована эффективная потенциальная энергия частиц в поле наклонного вращающегося магнитного диполя. Показано, что существуют замкнутые эквипотенциальные поверхности, которые совместно вращаются с полем диполя. В этих поверхностях заключены частицы с начальной энергией, ниже определенного уровня. Эффективная потенциальная энергия исследована на наличие экстремумов и найдены все стационарные точки. В качестве примеров построены эквипотенциальные поверхности для некоторых значений интеграла движения, для положительного и отрицательного заряда частицы и для различных значений магнитного момента небесного тела.

Потенциальная энергия, описываемая уравнением (2.17), найдена в соответствии с предположением, что намагниченное тело находится в вакууме и магнитосфера не заполнена плазмой. Но, как видно из последующего анализа, области захвата для частиц разного заряда расположены в разных пространственных областях. Вероятно, возможны условия, при которых области захвата накапливают настолько большой заряд, что он заметно искажает геометрию электромагнитного поля по сравнению с вакуумной магнитосферой. В этом случае следует решать самосогласованную задачу распределения плазмы в магнитосфере. Обсуждение этого вопроса можно найти в монографиях [8,35].

В окрестности тел с очень сильным магнитным полем, таких как нейтронные звезды, на релятивистские заряженные частицы действует сила радиационного трения, что приводит к потери энергии частиц. Хотя движение частиц с учетом радиационного трения не обсуждается в данной работе, исследование потенциальной энергии, тем ни менее, является мощным инструментом качественного анализа поведения частиц и в этом случае, так как конфигурация потенциальной энергии определяется только источником поля и не зависит от движения частиц. Очевидно, что если частица теряет энергию в процессе излучения, она переходит в состояния с более низкой энергией. Следовательно, граница допустимой области изменяется со временем, сдвигая частицу вниз по склону потенциальной энергии.

Тот факт, что в случае з • 从 > 0 отрицательно заряженные частицы концентрируются в полярных областях наклонного ротатора и частицы с положительным зарядом в экваториальной зоне, согласуется с выводами других авторов которые использовали различные модели для магнитосферы нейтронной звезды (см., например, [21,36,37]).

Результаты, полученные в настоящей работе, могут быть использованы для исследования радиационных поясов в окрестности конкретных небесных тел, магнитная ось которых не совпадает с осью вращения.