Динамика затопленного струйного течения в трубе в продольном магнитном поле

Движущиеся электропроводные жидкости, взаимодействующие с магнитным полем, являются существенным элементом многих промышленных процессов, систем и технологий. Особый интерес представляют струйные течения, встречающиеся в различных технических приложениях, например, в потоках при внезапных расширениях или при смешении, нагреве или охлаждении теплоносителей. Несмотря на разнообразие конфигураций в технических приложениях, свойства течений с сильным влиянием магнитного поля во многом определяются динамикой структур нескольких базисных типов, таких как «сдвиговые слои», вихревые структуры или струи. Такие структуры создаются либо непосредственно (примеры: струя, выходящая из патрубка в непрерывной разливке стали; сдвиговые слои около нагретых поверхностей), либо как результат неустойчивости (вихри, появляющиеся в результате конвективной неустойчивости опускных и подъемных течений в каналах).

Струйные течения в отсутствии магнитного поля изучаются достаточно давно. Свободные струи являются уже классическими задачами исследования сдвиговых течений и турбулентности [1].

В натурных и численных экспериментах затопленных струй существует проблема: необходимо исключать влияние вторичных течений на расход в струе, сказывающихся на автомодельности течения, а различия в граничных условиях на входе могут быть причиной существенного расхождения результатов [2–5].

При течении электропроводной жидкости в магнитном поле поток испытывает силовое воздействие со стороны поля, характеризуемое безразмерным числом Гартмана Ha = B 0 d^ о/ ( vp ) , где v, р, о — кинематическая вязкость, плотность, электропроводность жидкости соответственно, B ₀ — индукция магнитного поля, d — характерный масштаб длины. При этом важным является направление основной компоненты вектора магнитной индукции по отношению к осредненному течению. Наиболее существенное влияние оказывает поперечное магнитное поле. Осредненное течение при взаимодействии с магнитным полем имеет тенденцию к растяжению вдоль силовых линий и возникновению анизотропии у характеристик течения. Кроме того, магнитное поле подавляет в потоке вихревые структуры, так как приводит их к квазидвумеризации. Достаточно подробно эти явления описаны в теоретической работе [6]. Имеются другие исследования, которые в целом подтверждают эти выводы и показывают, что развитие под действием поперечного магнитного поля узких сдвиговых слоев, в которых сконцентрированы высокие градиенты скорости, способствуют росту потенциала для гидродинамической неустойчивости. Неустойчивость к двумерным или квазидвумерным возмущениям не подавляется или слабо подавляется магнитным полем, поэтому возможно их дальнейшее перерастание в крупномасштабные нестационарные когерентные структуры. Именно такой сценарий наблюдался, например, в работе [7], где изучалось течение круглой струи в поперечном магнитном поле.

Влияние продольного магнитного поля на течение проявляется гораздо слабее. В одной из ранних экспериментальных работ [8] рассматривалось турбулентное течение затопленной струи жидкого металла (ртути) с числом Рейнольдса Re = V 0 d /v = 9550 ( V₀ — средняя скорость струи на входе) и соотношении диаметра отверстия ( d ) к диаметру выходной трубы 1/10. Измерения скорости потока проводились с помощью термоанемометра и выявили зависимость формы профиля скорости струи от параметра МГД взаимодействия — числа Стюарта N = Ha²/Re при его изменении от 0 до 1. На основе анализа уравнений баланса импульса, с использованием характерных масштабов, предсказано и подтверждено экспериментально, что у свободной струи в сильном продольном магнитном поле ее скорость затухает как V ~ B 23 z ~^1/3 (здесь B — индукция магнитного поля, z — продольная координата). Таким образом, показано, что с увеличением магнитного поля диаметр струи уменьшается, а скорость в центральной части струи увеличивается. Также продемонстрировано, что магнитное поле снижает интенсивность турбулентности в областях, где градиенты средней скорости малы, и подавляет низкочастотные составляющие продольной скорости и высокочастотные составляющие скоростей вторичных течений. В экспериментальной работе [9] исследовалась ламинаризация круглой затопленной струи «индий–галлий– олово» с числом Re = 3300 и при соотношении диаметров струи и канала 1/5 под действием продольного магнитного поля и выявлено увеличение эффективной длины струи под действием магнитного поля. В расчетных работах [10, 11] рассматривалась круглая затопленная струя с числом Re = 1800 при истечении в канал квадратного течения и соотношении диаметр струи/сторона канала, равном 1/8. Получено подтверждение эффекта подавления турбулентности и затягивания перехода к турбулентности за счет стабилизирующего действия поля. Дана оценка для эффективной длины струи в зависимости от числа Гартмана La ~ Ha¹² (где a — полуширина канала). Выяснено, что при определенном значении числа Гартмана в потоке развивается неустойчивость в виде бегущих продольных и круговых волн, генерируемых взаимодействием вторичных радиальных течений и магнитного поля. Обнаружена цикличность процесса образования и затухания этих волн. Вместе с тем авторы этих работ оставили без внимания некоторые вопросы, например, что инициирует волновой процесс, какова роль геометрических особенностей, нарушающих осевую симметрию, в развитии возникающих возмущений.

Мотивация настоящей работы связана с желанием продолжить исследования влияния продольного магнитного поля на динамику затопленной струи в условиях, близких к взятым в [11]. Поставлена цель рассмотреть потоки при более высоких числах Рейнольдса, что ближе к практическому применению результатов, а также проанализировать влияние геометрической формы канала на эффекты в затопленной струе в сильных магнитных полях, выявленные в работе [11].

• 2.    Методы исследований

  • 2.1.    Постановка задачи

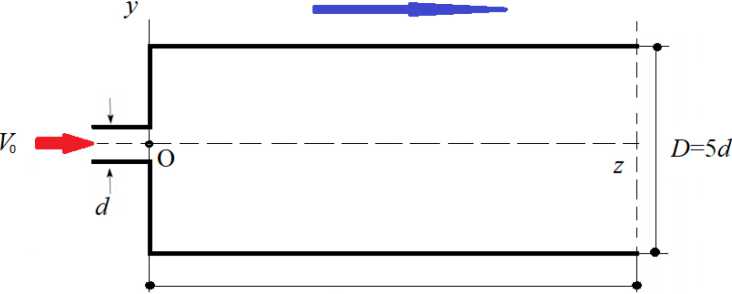
Исследуется затопленное струйное течение электропроводящей жидкости в трубе (Рис. 1), образующееся при внезапном расширении потока при истечении из отверстия трубы меньшего диаметра d в трубу большего диаметра D , заполненную той же жидкостью.

а

в

L=5M

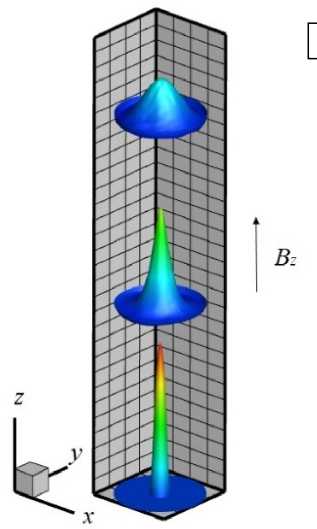
Рис. 1. Схема к постановке задачи: геометрия расчетной области в сечении плоскостью O yz ( а ); 3D вид расчетной области ( б )

Струйное течение формируется на входе в расчетную область, при ( z = 0). Расчетная область имеет форму трубы диаметром D = 5 d. Длина расчетной области составляет L(D = 10 калибров или L/d = 50 калибров в диаметрах струи и выбиралась достаточной для моделирования условий в верификационных экспериментах при сохранении динамики струи и без существенного влияния на результат граничных условий на выходе. На расчетную область течения накладывается пространственно однородное и не зависящее от времени продольное магнитное поле B { 0,0, B_z = B₀ } .

• 2.2.    Физическая модель и численное моделирование

Физическая модель представляет собой изотермическое и несжимаемое течение электропроводящей жидкости с постоянными физическими свойствами и постоянным расходом через расчетную область.

Рассматривается квазистатическое (безындукционное) приближение магнитной гидродинамики [16], которое можно использовать при условии малости магнитных чисел Рейнольдса Re m = V₀ d ац ₀<<1 и Прандтля Pr m = Re m /Re = v^p ₀ <<  1 ( p ₀ — магнитная проницаемость вакуума). Суть приближения состоит в том, что, во-первых, внешнее приложенное магнитное поле B много больше, чем возмущения магнитного поля b , вызванные электрическими токами, индуцируемыми в жидкости. Во-вторых, индуцированное поле мгновенно перестраивается при изменении скорости потока. Таким образом, в квазистатическом приближении диффузия магнитного поля преобладает над его адвекцией. Взаимодействие движущейся электропроводящей среды и магнитного поля сводится к одностороннему влиянию магнитного поля на течение. Тогда закон Ома и выражение для электромагнитной силы можно записать в виде:

j = о ( -Vф + v х B ) ,

Fl = j х B, а для замыкания системы уравнений, принимая во внимание закон Кирхгофа div j = 0 , получим уравнение Пуассона для электрического потенциала:

V²ф = V- ( v х В ) .

Учитывая вышеперечисленные допущения, вводя безразмерный вектор магнитного поля eb = В/ B ₀ и пренебрегая вязкой и джоулевой диссипацией, придем к 3D системе уравнений физической модели течения в безразмерном виде:

— + (V • V) V = -Vp + Re-1 V2 V + Ha2Re-1 (j х eb),(4)

V. V = 0 ,(5)

j = -Vф + V х Cb ,(6)

V2 ф = V.( V х сь),(7)

в которых в качестве масштабов используются: для координат — диаметр d трубки, формирующей струю;

для скорости — средняя скорость жидкости V 0 на входе; для времени — d/V 0 ; для давления — р V 02 ;

для электрического потенциала — V 0 B 0 d ; плотности тока — a V 0 B 0 .

Безразмерными параметрами задачи (4)-(7) являются число Рейнольдса Re = V 0 dV , число Гартмана Ha = B 0 d ^ о/ ( vp ) или число Стюарта N = Ha² /Re .

Граничные условия для скорости на твердых стенках — условия прилипания. На выходе из расчетной d V     d V           __/7/__Х2

области применяется конвективное условие для вектора скорости:    + Uo — = 0, где Uo = Vo (d D) — dt     0 дx               0    0

средняя скорость на выходе из расчетной области. Профиль скорости на входе параболический (Рис. 1 б ) со случайными возмущениями 0.1% от средней скорости V ₀ . Стенки трубы принимались электроизолированными и в расчете не учитывались, поэтому на всех границах расчетной области, задавалось условие равенства нулю нормальной компоненты плотности электрического тока:

j n ст

дф

= 0.

Задача решалась методом прямого численного моделирования (Direct Numerical Simulation — DNS) с помощью консервативной конечно-разностной схемы второго порядка на структурированной совмещенной сетке в цилиндрических координатах r , 0 , z . Ее точность и эффективность при моделировании течений с высокими числами Гартмана продемонстрирована, например, в [14]. Моделирование проводится на сетке из N = N_r х N ₀ х N_z = 128 х 192 х 1024 узлов, равномерной по оси z и углу 0 и неравномерной по r , со сгущением к стенкам трубы ( r = R 0 = D /2) и к центру ( r = 0 ). Количество узлов подбиралось из предварительных расчетов для оценки сеточной сходимости.

• 2.3.    Экспериментальные исследования

Эксперименты проводились на уникальной научной установке «Ртутный МГД-стенд» [12]. В качестве рабочей жидкости использовалась ртуть. Схема экспериментального контура показана на рисунке 2. Продольное магнитное поле создается с помощью соленоида 2 с внутренним диаметром 30 мм и длиной обмотки 700 мм, обеспечивающего постоянное однородное (с точностью 5%) магнитное поле с индукцией до В ₀ = 0,92 Тл

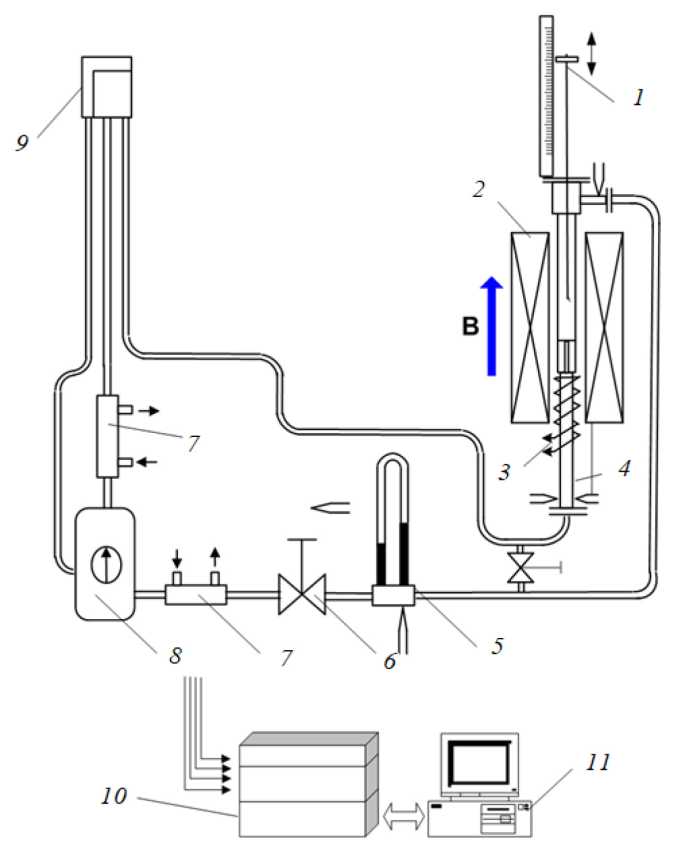
Рис. 2. Схема экспериментального стенда: 1 – зонд, 2 – соленоид, 3 – нагреватель, 4 – рабочий участок, 5 – расходомер, 6 – запорно-регулировочный вентиль, 7 – холодильники, 8 – резервуар с ртутью и насос, 9 – бак постоянного уровня, 10 , 11 – система измерений

в рабочем участке 4 на длине около 600 мм. Реализовано подъемное течение жидкого металла в вертикальной обогреваемой составной трубе. Расположение рабочего участка 4 обеспечивает формирование затопленной струи в области однородного продольного магнитного поля.

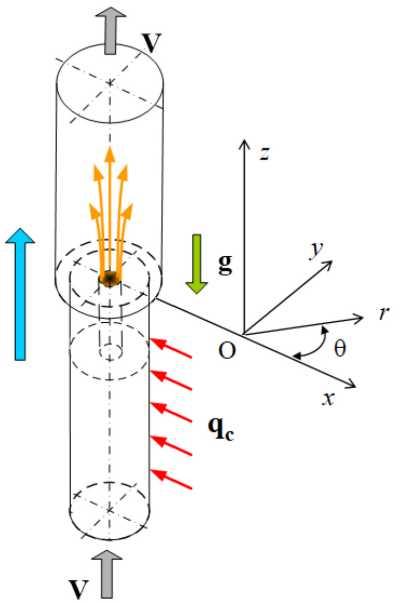
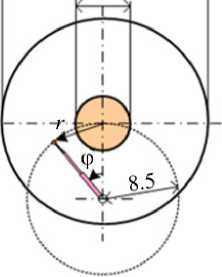
Рабочий участок (Рис. 3) состоит из трех последовательно соединенных тонкостенных нержавеющих труб: входной трубы, которая имеет внутренний диаметр 18 мм и длину 700 мм; переходной трубки диаметром d = 5 мм и длиной 100 мм, формирующей затопленную струю; трубы диаметром D = 25 мм и длиной 600 мм, которая заканчивается камерой смешения с выходным патрубком. Последняя и является областью исследования. На наружной поверхности входной трубы установлен нагреватель косвенного обогрева, создающий тепловые неоднородности в потоке ртути, что необходимо для применения в изучаемой области вниз по потоку корреляционной методики измерения скорости [13]. Навитый на трубу нагреватель изготовлен из нихромовой ленты 8×0.2 мм², продетой в чулок из стеклоткани. Питание нагревателя осуществляется переменным током через автотрансформатор.

Для проведения двумерных измерений локальных характеристик поля компоненты

б

Рис. 3. Фотография ( а ) и схема конфигурации ( б ) рабочего участка в эксперименте

скорости v_z ( r , z ) и температуры T ( r , z ) в исследуемой области используется продольный зонд 1 (см. Рис. 2) с датчиком из двухмедь-константановых микротермопар (Рис. 4 а ) с оголенными спаями диаметром 5 = 0.2 мм, расположенными на линии тока на расстоянии l ₁₂ = 4.37 мм друг от друга. Датчик вмонтирован на конце трубки продольного зонда диаметром 8 мм, эксцентрично расположенного по оси трубы рабочего участка диаметром 25 мм. При этом центрирующие кольца зонда обеспечивают сохранение радиальных координат термопар с точностью 0.1 мм. Координата r положения датчика определяется (Рис. 4 б ) как длина хорды окружности с известным радиусом вращения зонда £ = 8.5 мм и по углу поворота ф , который измеряется по угловому «лимбу» в градусах: r = 2 £ sin ( ф/ 2 ) . Положение зонда в продольном направлении

z определяется по линейной шкале.

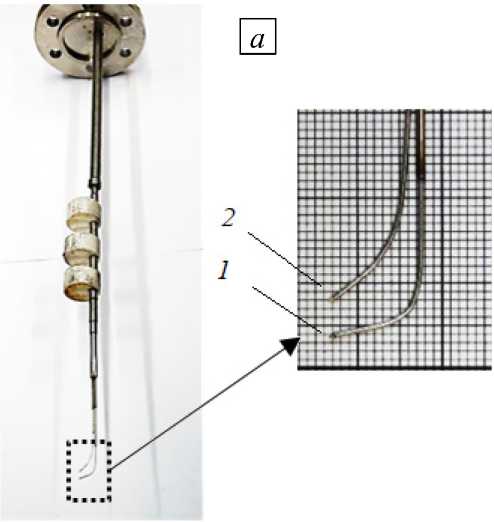
а

Рис. 4. Продольный зонд (а) с двумя микротермопарами и эксцентричным положением (б)

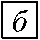
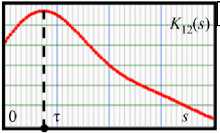
Профили скорости измеряются корреляционным методом (Рис. 5), в котором естественный фон турбулентных флуктуаций температуры полагается «пассивной примесью», переносимой потоком [13]. При фиксированном известном расстоянии между термопарами l ₁₂ (Рис. 5 а ) усредненную продольную компоненту скорости течения в месте расположения датчика можно определить, зная т — время задержки сигнала второй термопары T ₂ ( t ) относительно первой T 1 ( t ) (Рис. 5 б ):

v= = ^l 12 /^Т ■

Время задержки т соответствует координате 5 максимума на кривой K12 (5) взаимно-корреляционной функции (ВКФ) (Рис. 5в), оценку

которой можно определить при обработке оцифрованных временных сигналов микротермопарных датчиков

T 1 ( t ) и T ( t ) :

K12 (5 ) = N 2 NT (iА t) T (iЛ t + 5 ) .

Здесь: 5 — параметр ВКФ (сдвиг по времени), 5 = k ^ t ( к = 0,1,..., m ); A t — шаг по времени, определяемый частотой опроса измерителя; N — объем выборки.

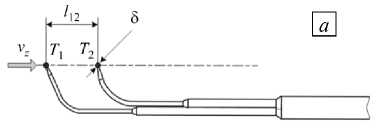
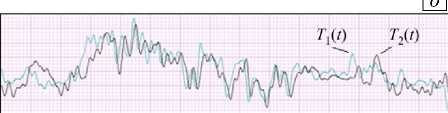
Рис. 5. К определению продольной скорости с помощью корреляционной методики: положение термопар ( а ), сигналы с термопар ( б ), график взаимно-корреляционной функции ( в )

в

3.    Результаты

Экспериментальные исследования осуществлялись для чисел Рейнольдса, Гартмана и Стюарта в диапазонах: Re = 10 4 + 4 -10 4 ; Ha = 0 ^ 100 ; N = 0 ^ 1. Численное моделирование проведено по результатам анализа натурных испытаний для наиболее актуального числа Рейнольдса, равного 10⁴, и вариациях числа Гартмана до 180 ( N ~ 3.0), что позволило расширить обычно используемые в вычислительных экспериментах диапазоны параметров рассматриваемого явления.

Осредненные экспериментальные данные измерений продольных скоростей потока представлены в дальнейшем в виде распределений по пространственным координатам r и z . Для получения полей интересующих величин в численном моделировании результаты усреднялись на квазистационарных по кинетической энергии потока временных интервалах длиной порядка 1000 безразмерных единиц времени, что составляет 10^20 конвективных временных единиц (1c.u. = R 0 U 0 ), рассчитанных по радиусу и средней скорости на выходе из расчетной области.

• 3.1.    Течение в отсутствие магнитного поля

  Вычислены мгновенные поля продольной скорости в вертикальном осевом сечении трубы (см. Рис. 6 а , в ), которые показывают пространственное развитие затопленный струи для двух чисел Рейнольдса. При Re = 20000 обращает на себя внимание осевая нестабильность струи, связанная с воздействием вторичных течений. Эти течения развиваются в том числе из-за близости стенки и хорошо видны при z d ~ 15 на средних полях продольной скорости, представленных на рисунке 6 б , г , на которые также нанесены векторные линии поля скорости в рассматриваемой проекции. За указанным сечением струйное течение фактически не различимо в потоке, поэтому анализ усредненных величин и турбулентных статистик, представленный далее, проводился на участке 5 <  zjd <  10 .

На рисунке 7 а представлено изменение усредненной осевой скорости течения в зависимости от расстояния от входа. Имеет место неплохое качественное совпадение экспериментальных и расчетных данных, в то время как количественное расхождение результатов связано, по-видимому, с заданием в расчете параболического профиля скорости входного потока, что не вполне реалистично. Также видно соответствие трансформации струи на участке 5 <  z/d <  10 автомодельному решению V c ~ z для истечения струи в неограниченном объеме, полученным в работе [1].

Усредненные по времени профили продольной скорости в зависимости от автомодельной координаты r/z на участке осреднения 5 <  z/d <  10, который дает наиболее похожий на автомодельное решение результат, показаны на рисунке 7 б . Данные численного моделирования и эксперимента неплохо совпадают, но количественно отличаются от результатов работ [1], [3] и [15], приведенных на рисунке. Отклонения могут объясняться различными входными условиями, и, что более значимо, существенно меньшим в обсуждаемом случае соотношением Dd, которое усиливает влияние стенок на течение. В потоке развиваются вторичные течения, которые дают отрицательные значения усредненной скорости потока при r z >0.12 , что подтверждается и экспериментальными данными. Усредненный профиль скорости, полученный в эксперименте, качественно подтверждает результаты моделирования.

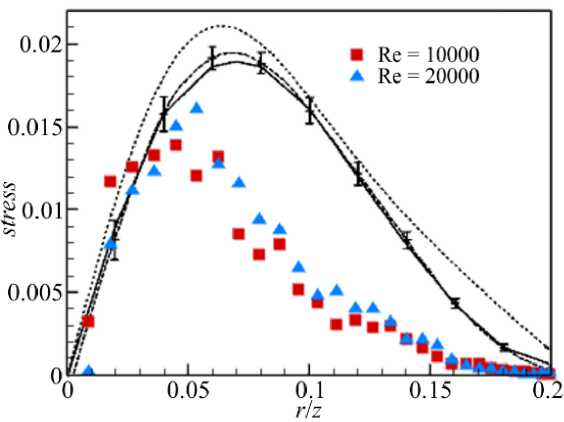
Распределения статистических характеристик турбулентных флуктуаций скорости в зависимости от отношения rz показаны на рисунке 8. На фрагментах ( а ) –( в ) представлены распределения среднеквадратических отклонений флуктуаций компонент скорости, отнесенных к локальной осевой

'2

скорости: rms V Vc лок = W Vc лок , а на фрагменте (г) — распределение турбулентных напряжений, отнесенных к квадрату локальной осевой скорости: stress = VrVzVcлок . Результаты численного моделирования имеют качественное сходство с имеющимися данными экспериментов и расчетов в работах с неограниченными струями [1], [3], [4] и [15], а отличия в профилях статистических характеристик связаны с влиянием вторичных возвратных течений. Максимумы интенсивностей пульсаций скорости приходятся на область, находящуюся ближе к центральной части струи, что объясняется наличием здесь максимума градиента осредненной скорости. Но при этом максимум более выражен, что, как показано в работе [8], свойственно для струй, ограниченных стенками, и связано с влиянием вторичных течений. При увеличении r z интенсивность флуктуаций снижается, а в области влияния возвратных течений (при r/z ^ 0.2) вновь начинает возрастать.

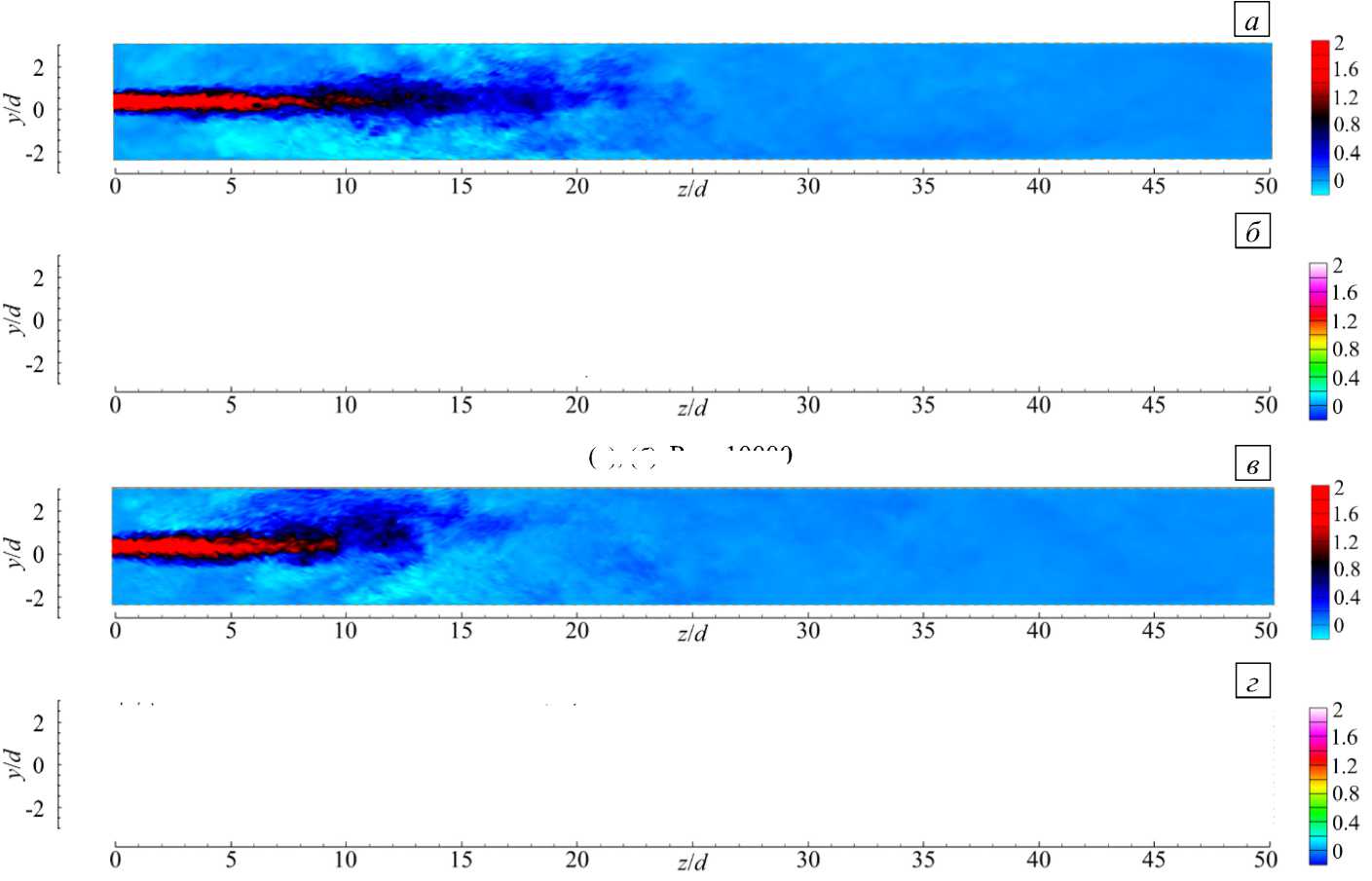
( а ), ( б ) Re = 10000

( в ), ( г ) Re = 20000

Рис. 6. Поля продольной компоненты скорости V в вертикальном осевом сечении расчетной области ( x = 0) при Re = 10000 ( а ) , ( б ) и Re = 20000 ( в ) , ( г ) и векторное поле скорости в проекции на плоскость O yz ( б), ( г );

мгновенная продольная скорость отнесена к средней скорости V_z V ₀

( а ) , ( в ); усредненная продольная скорость отнесена

к локальной осевой скорости V_z V_{c , лок} ( б ) , ( г )

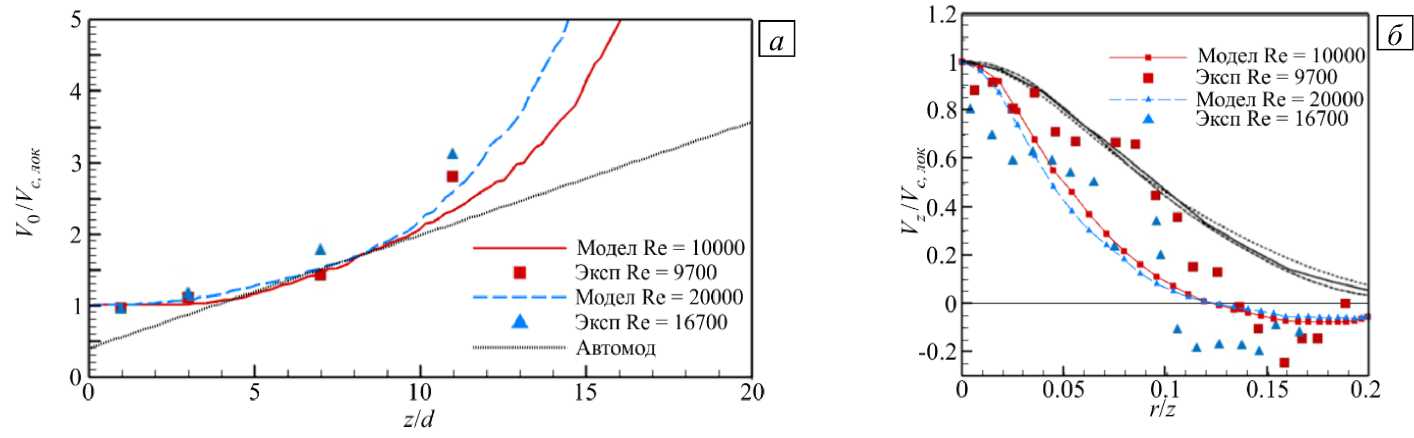
Рис. 7. Распределение усредненной осевой скорости V ₀ V_{с , лок} по длине канала (пунктирная линия – автомодельное решение

V_c ¹ ~ z из работы [1]; точки - эксперимент; сплошные линии - расчет) ( а ); профили усредненной продольной скорости

V_z V_{c , лок} в зависимости от автомодельной координаты rz (данные из работ других авторов: ∙∙∙ из [1]; --- из [3]; — из [15]) ( б )

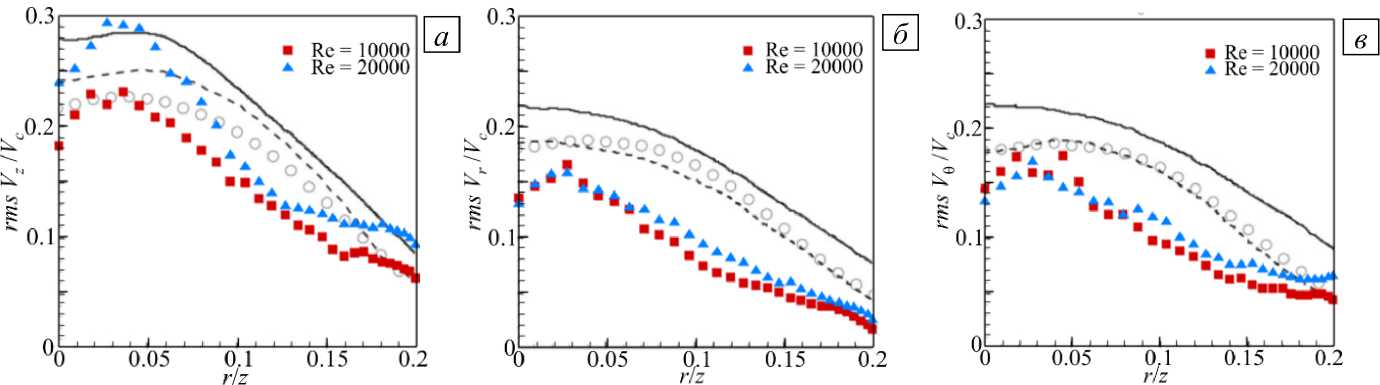
Рис. 8. Профили статистических характеристик турбулентных флуктуаций скорости в зависимости от автомодельной координаты rz : ( а )–( в ) – среднеквадратические отклонения ( rms ) флуктуаций, соответственно, продольной, радиальной и азимутальной компонент скорости, отнесенные к локальной осевой скорости потока V c лок ; ( г ) - турбулентные напряжения ( stress ), отнесенные к квадрату локальной осевой скорости потока V c ² лок ; авторские результаты расчета изображены цветными символами; данные из работ других авторов: на фрагментах ( а )-( в ) — из [15]; ооо - DNS из [4]; — из [1]; на фрагменте ( г ) — из [3], ••• из [1], — из [15]

• 3.2.    Влияние магнитного поля на усредненное течение

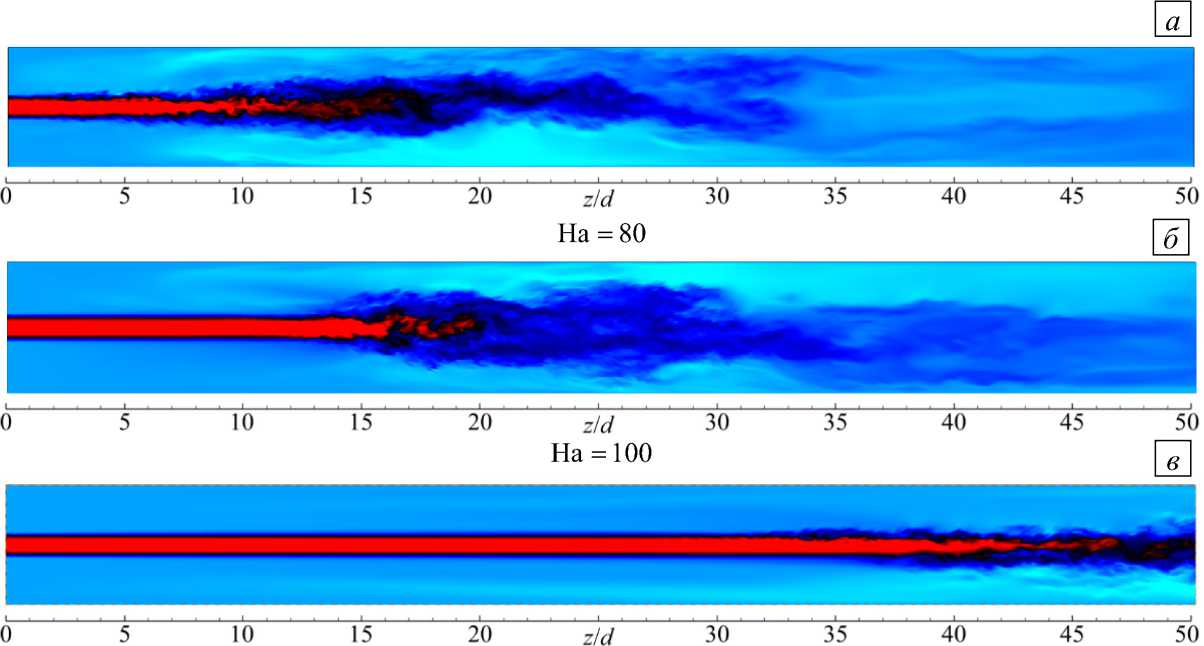
Мгновенные поля продольной скорости, полученные в численном моделировании для различных чисел Гартмана показаны на рисунке 9. С увеличением числа Гартмана уменьшаются флуктуации скорости, а усредненные поля скорости вытягиваются в продольном направлении, таким образом, эффективная длина струи становится больше. Изменения в структуре течения подтверждает и поведение кинетической энергии флуктуаций скорости ( к = ( 1/2 ) Е V i '² ), отнесенной к квадрату средней скорости V 0 . Распределения энергии k , усредненной в сечении трубы по длине канала, представлены на рисунке 10 а . Видно, что с увеличением числа Гартмана снижается абсолютный уровень флуктуаций, максимум же отодвигается в область фронта струи, где течение становится турбулентным, и после — канальным. Так, на участке 0 <  z/d <  10 при Ha = 80 течение в значительной степени ламинаризуется, при этом энергия флуктуаций уменьшается по сравнению со случаем отсутствия магнитного поля (Ha = 0), однако существенно превышает энергию флуктуаций фактически ламинарного на этом участке течения (при Ha = 100).

Ha = 120

Рис. 9. Поля мгновенной продольной компоненты скорости V s (V_o в вертикальном осевом сечении расчетной области ( x = 0 ) при Re = 10000 и различных числах Гартмана Ha : 80 ( а ), 100 ( б ), 120 ( в )

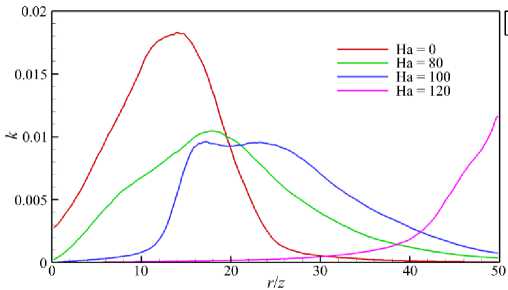
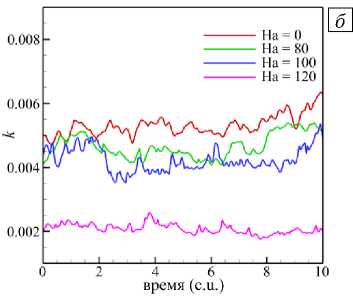
Рис. 10. Распределение кинетической энергии флуктуаций скорости к при Re = 10000 и различных числах Гартмана по длине

канала ( а ) и во времени ( б ); энергия k усреднена по сечению трубы в плоскости O yz ( а ) и по объему расчетной области ( б )

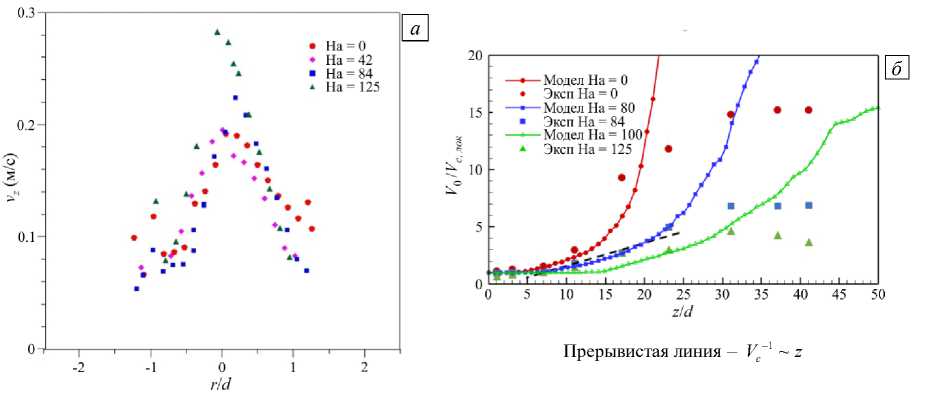
Рис. 11. Профиль усредненной продольной скорости распределение обратной

Vz (r,d) в сечении трубы z/d = 1.0 (а) и усредненной осевой скорости V0JVc лок (б) по данным измерений и моделирования при различных числах Гартмана и Re = 10000

Затем течение вниз по потоку при Ha = 100 турбулизируется и практически достигает уровня флуктуаций при Ha = 80 . При Ha = 120 на большей части участка преобладает ламинарное течение с профилем скорости, близким к заданному на входе. Таким образом, магнитное поле «тормозит» переход к турбулентности ближе к «фронту» струи. Среднеобъемная k , представленная на рисунке 10 б в зависимости от времени и числа Гартмана, также уменьшается по абсолютной величине, что свидетельствует о подавлении турбулентного переноса с ростом числа Гартмана.

Сделанные ранее в работах [8] и [9] измерения средней продольной скорости в эксперименте качественно подтверждают выводы о влиянии продольного магнитного поля на динамику течения. Форма профиля скорости при увеличении индукции магнитного поля изменяется: в центре струи скорость увеличивается, а ширина струи уменьшается (Рис. 11а). Значения осевой скорости в магнитном поле (Рис. 11б) качественно

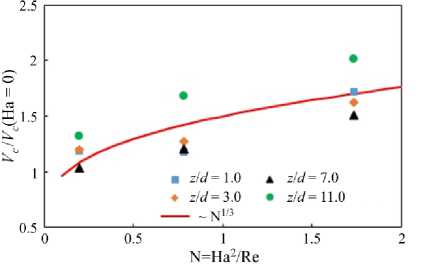
Рис. 12. Изменение по длине трубы осевой скорости, нормированной по осевой скорости в отсутствие магнитного поля ( На = 0 ), в зависимости от числа Стюарта N = Ha²/Re

укладываются в линейную зависимость Vc-1 ~ z, характерную для струи, вытекающей в неограниченное пространство. Это свидетельствует об уменьшении влияния стенок на течение. Вследствие подавления турбулентного переноса под действием магнитного поля и ламинаризации течения длина «линейного» участка на графике возрастает до zd~ 20 . Данные моделирования и расчета неплохо совпадают до zd~ 20 , затем наблюдается существенное расхождение, что, по-видимому, связано с увеличением погрешности экспериментальной корреляционной методики ввиду сглаживания температурных флуктуаций в эксперименте с ростом zd. Динамика расширения струи в продольном магнитном поле, качественно обоснованная в работе [8], воспроизводится по экспериментальным данным. Так, например (см. Рис. 12), осевая скорость, нормализованная по скорости в отсутствие магнитного поля для различных сечений вдоль по потоку, пропорциональна числу Стюарта ~N13 .

Устойчивость ламинаризованной струи и увеличение ее эффективной длины в магнитном поле обеспечиваются вторичными возвратными течениями жидкости, которые создают ее радиальный поток к границе между струей и окружающей жидкостью, с одной стороны, и между струей и обратным радиальным потоком расширяющейся струи, с другой стороны. Оба этих течения при взаимодействии с продольным магнитным полем индуцируют в жидкости преимущественно азимутальные компоненты электрического тока j ₉ ~ Vr.B z в разных по углу 9 направлениях. Со стороны магнитного поля на жидкость, таким образом, действует электромагнитная сила F_r ~ j ₉ B z , которая, в зависимости от величины поля (числа Гартмана) и числа Рейнольдса (или, в общем случае, от числа Стюарта N ) определяет форму профиля скорости струи. Эти соображения подтверждаются результатами численного моделирования.

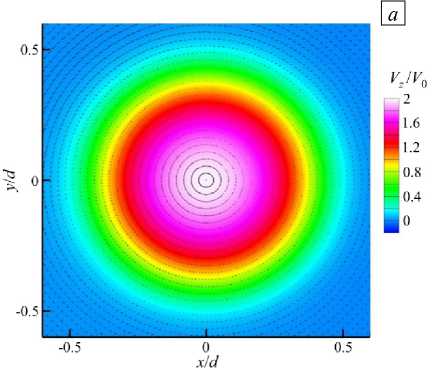
Рис. 13. Поле мгновенной продольной скорости V_z V ₀

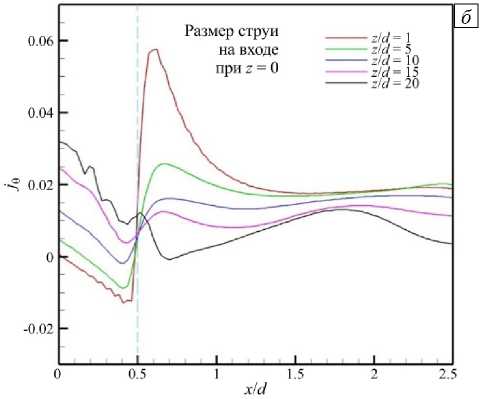
в сечении z]d = 1.0 и векторное поле индуцированного

электрического тока (а); распределение азимутальной компоненты плотности электрического тока j9 (б) в радиальном направлении вдоль оси x при На = 120, Re = 10000

На рисунке 13 а представлено мгновенное поле продольной скорости в сечении z]d = 5 , а также векторные линии электрического тока j ( j_x , j y ) при На = 120. Видно, что в потоке вне профиля струи формируется поле плотности электрического тока с преобладающей компонентной j ₉ , а радиальная компонента электромагнитной силы F_r удерживает струю от расширения в радиальном направлении. Распределение j ₉ вдоль одного из диаметров в разных сечениях zd показано на рисунке 13 б . Видно, что при увеличении zd максимум азимутального тока уменьшается по величине и смещается вправо вдоль оси x , что означает постепенное расширение струи и снижение воздействия электромагнитной силы, удерживающей струю.

• 3.3.    Влияние магнитного поля на устойчивость течения

При численном моделировании устойчивая структура струйного течения с практически подавленными возмущениями и ламинарным усредненным профилем скорости на расстоянии эффективной длины струи, а также с переходом к турбулентности во фронтовой части струи сохраняется вплоть до значений числа На ~140 . В эксперименте же не было технической возможности увеличить число Гартмана выше 130, поэтому результаты, приведенные далее, получены только с помощью численного моделирования.

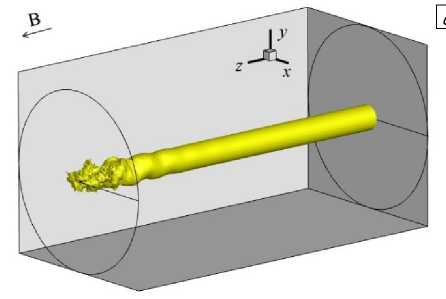
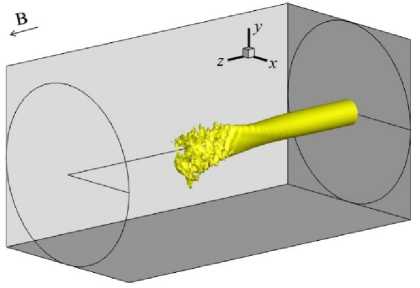
При дальнейшем увеличении числа Гартмана течение в струйном потоке приобретает колебательный характер. Так, уже при На = 120 струя начинает испытывать возмущения профиля скорости в его ламиниризованной части ближе к фронту. На рисунке 14 а , б в различные моменты времени для На = 120 представлены изоповерхности продольной скорости, равной средней скорости V ₀ . Видно наличие поперечных колебаний изоповерхности скорости, причем эти колебания являются периодическими и распространяются с постепенным затуханием от фронта к началу канала, то есть течение остается устойчивым, за исключением участка фронта струи, а эффективная длина струи не меняется.

в

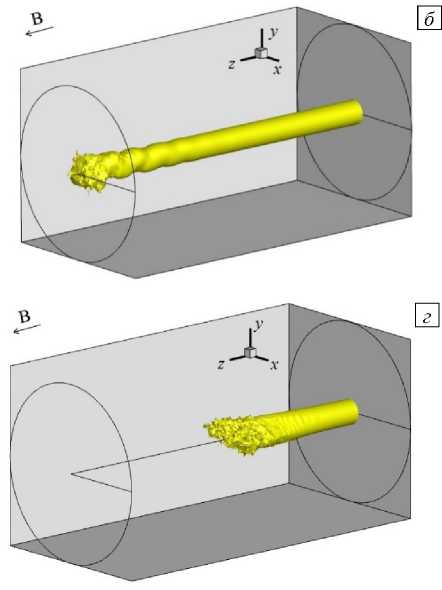
Рис. 14. Изоповерхность продольной скорости V z = V о при Re = 10000 в моменты времени 1 1   ( а ), ( в ) и 1 2   ( б ), ( д );

На = 120 ( а ), ( б ); На = 160 ( в ), ( д ); Д 1 = 3.0 c.u.; размер канала в продольном направлении показан в масштабе 1:5

Другая картина возникает при дальнейшем увеличении числа Гартмана. Так, при На = 160 (Рис. 14 в , г ) фронт струи становится неустойчивым, что приводит к уменьшению эффективной длины струи почти вдвое. Вместе с тем колебания изоповерхности существенно уменьшаются, а фронтальная часть струи начинает «закручиваться», при этом ось вращения совпадает с направлением основного течения.

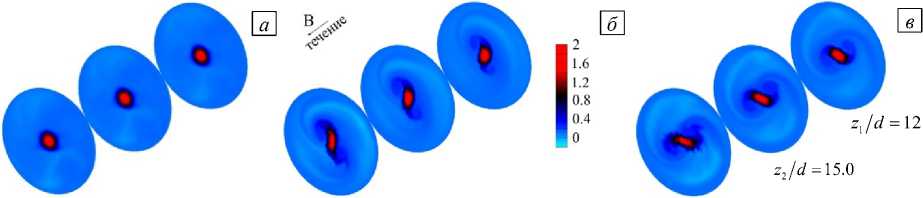
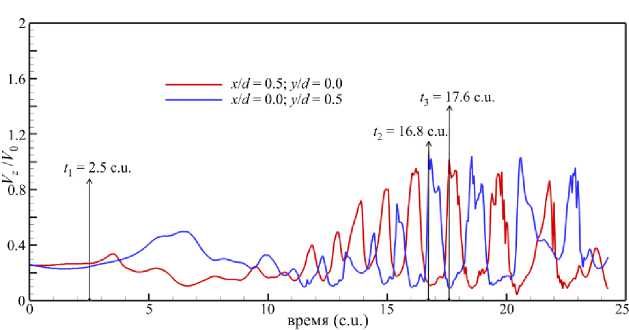
Развитие течения при На = 160 демонстрируется рисунке 15. Изменение симметрии профиля струи хорошо видно для разных поперечных сечений ( z ₁, z ₂, z ₃), которые изображены в моменты времени ( t ₁, t ₂, t ₃) (Рис. 15 а – в ). Эволюция во времени продольной скорости в фиксированных точках 1 и 2 , изображенных на схеме (см. Рис. 15 д ), показаны на рисунке 15 г . Видно, что в момент времени t ₁ форма профиля струи (Рис. 15 а ) представляет собой окружность, что соответствует состоянию вытянутой и ламинаризованной струи (как, например при На = 120, в подразделе 3.2). Флуктуации продольной скорости вблизи t ₁ практически отсутствуют. В дальнейшем происходит увеличение флуктуаций скорости, появляются периодические низкочастотные сигналы на зависимостях продольной скорости от времени, полученных в точках 1 и 2 . Эти сигналы указывают на изменение во времени положения (то есть на «поворот») профиля струи, при этом сам профиль деформирован и уже не имеет формы окружности: он растягивается в одном диаметральном сечении и сжимается в другом. В моменты времени t ₂ и t ₃ положение профиля струи показано на рисунке 15 б , в , соответственно, при этом сигналы 1 и 2 находятся в противофазе друг другу. Характерный период колебаний продольной скорости в точках 1 и 2 равен ~0.8 c.u., что позволяет оценить период вращения как ~1.6 c.u. Такой режим является нестабильным, в дальнейшем градиенты продольной скорости выравниваются, поэтому амплитуда флуктуаций снижается (см. Рис. 15 г при 1 ^ 25 c.u.).

При дальнейшем увеличении числа Гартмана вращение сохраняется и имеет тенденцию сохранять квазистационарность с некоторой «перемежаемостью» (чередованием во времени) двух различных режимов течения. Так, для Ha = 180 на рисунке 16 а - в приведены профили продольной скорости в сечении zjd = 15.0 в разные моменты времени, соответствующие, как видно на графике рисунка 16 г , появлению максимумов продольной скорости в точке с координатами x/d = 0 и y/d = 0.75 . Формы профилей скорости показывают, что возникновение интервалов с большей амплитудой флуктуаций скорости (Рис. 16 а , в ), вероятно, связано с потерей устойчивости течения на фронте струи, поскольку появляются высокочастотные составляющие на зависимостях компонент скорости от времени (Рис. 16 г ). Характерный период «вращения», определяемый как удвоенное время между двумя соседними максимумами скорости, остается таким же, как и при Ha = 160 .

z 3/ d = 17.5

t ₁ = 2.5

t 2 = 16.8

г

Рис. 15. Пространственная эволюция течения при На = 160, Re = 10000: мгновенные поля продольной скорости VJV 0

в трех последовательных поперечных сечениях плоскостью O yz : z/d = 12.5; 15.0; 17.5, в разные моменты времени t , [c.u.]: 2.5 ( а ), 16.8 ( б ); 17.6 ( в ), и эволюция во времени продольной скорости ( г ) в точках c координатами x/d = 0.5 , y/d = 0.0 и

1 ₃ = 17.6

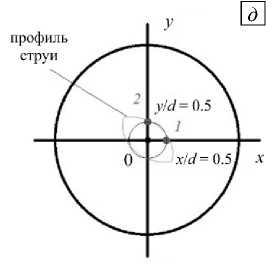
xd = 0.0, y/d = 0.5 в сечении z/d = 15.0 (см. схему ( д ))

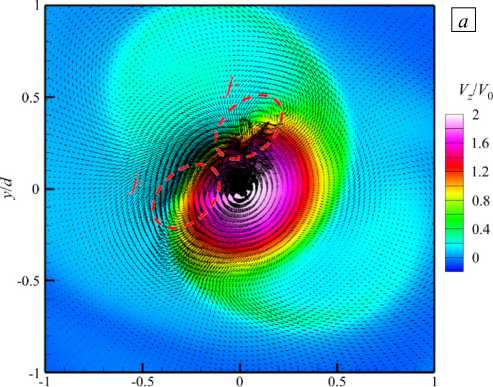
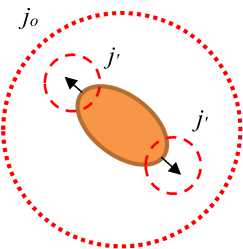
Нарушение симметрии профиля струи при высоких числах Гартмана (которым отвечают взятые в расчетах числа Стюарта N >  1) может быть вызвано двумя причинами. С одной стороны, это неустойчивость, которая развивается вблизи фронта струи и приводит к сложной картине развития вторичных течений, влияющих на распределение индуцированных токов, с другой — увеличение интенсивности вторичных течений по мере роста индукции магнитного поля. На рисунке 17 а представлено поле продольной скорости и векторное поле индуцированных токов в вертикальном поперечном сечении z/d = 15 при Ha = 180. Видно, что деформация струи поддерживается индуцированными токами, радиальные компоненты которых направлены к центру струи (на рисунке отмечено штриховой линией). Возможная качественная схема развития деформации формы профиля струи содержится на рисунке 17 б . Стационарное распределение плотности индуцированных токов, в которых основная азимутальная компонента тока j _в определяла контур тока j o (пунктирная окружность, см. Рис. 17 б ) изменяется под действием вторичных течений жидкости. В потоке вблизи границы струи локально становится

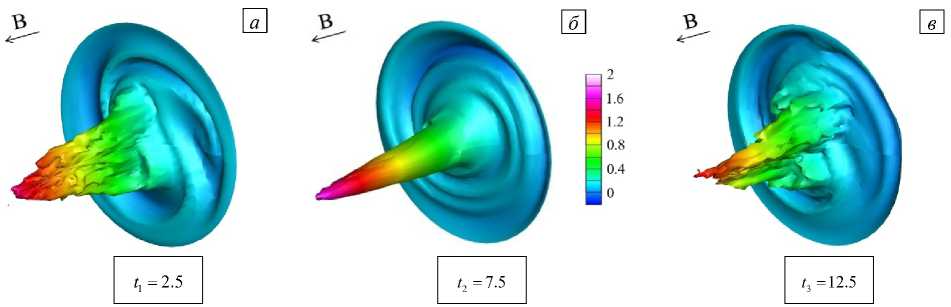
Рис. 16. Эволюция течения при На = 180, Re = 10000 ; мгновенные поля продольной скорости VJV0 в поперечном сечении z/d = 15.0 в разные моменты времени t, [c.u.]: 2.5 (а), 7.5 (б); 12.5 (в), и эволюция во времени компонент скорости (г) в точке

x/d = 0.0 , yId = 0.75

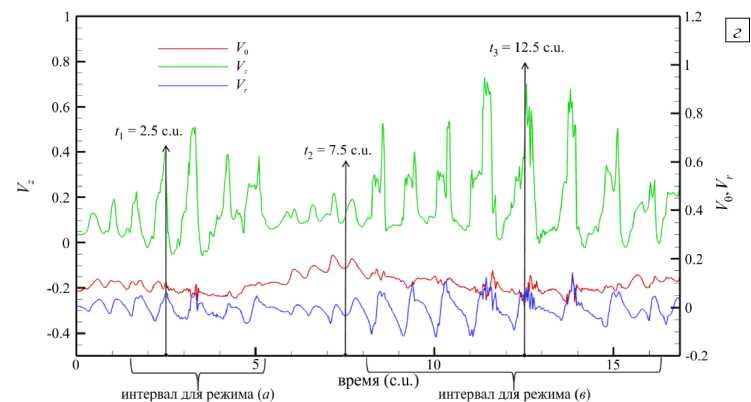
Рис. 16. Продолжение

x/d

Рис. 17. Поле мгновенной продольной скорости V_z V ₀ в сечении

б

zjd = 15.0 и векторное поле индуцированного электрического тока (а); качественная схема возникновения деформации струи (б) при На = 180 , Re = 10000

существенной радиальная компонента тока j_r , что обусловливает возникновение дополнительных контуров тока j ’ (пунктирные линии на рисунке 17 а , б ). Это, в свою очередь приводит, во-первых, к локальному

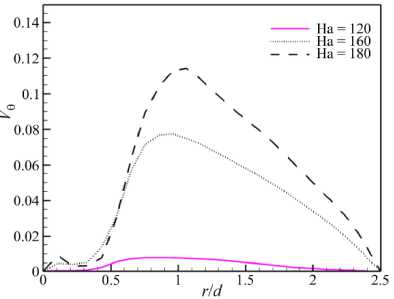
Рис. 18. Профили усредненной по углу азимутальной скорости Vz V0   в сечении z/d = 15.0 при Re = 10000 и различных числах

Гартмана

уменьшению азимутальной компоненты в контуре ( j_o ) и к появлению радиальных, растягивающих струю, усилий со стороны магнитного поля, а во-вторых, возникает локальная азимутальная компонента электромагнитной силы F ~ j r B z , которая может способствовать дополнительной локальной закрутке потока. Зависимость усредненной азимутальной скорости потока от числа Гартмана демонстрирует рисунок 18. С ростом числа Гартмана максимум азимутальной скорости увеличивается (при На = 180 он составляет ~12% от средней скорости потока) и смещается в радиальном направлении.

4.    Выводы

Рассмотрена динамика затопленного струйного течения проводящей жидкости (жидкого металла) в трубе при соотношении диаметров d/D = 1/5 , Re = 10000 и числах Гартмана до 180, что соответствует числам Стюарта до ~3.0. Исследования проводились в основном с помощью численного моделирования, а экспериментальная методика использовалась для верификации и сопоставления результатов усредненных свойств потока.

В отсутствие магнитного поля вблизи стенки под действием вторичных возвратных течений струя быстро расширяется и на расстоянии от начала канала до 30 калибров в диаметрах струи течение становится канальным. Длина перехода в канальное течение, как и ожидалось, зависит от величины числа Рейнольдса. Усреднение профиля скорости на участке 5 <  z/d <  10 дает неплохое соответствие результатов эксперимента и моделирования известным из литературы данным как по усредненным, так и по статистическим характеристикам.

При умеренных магнитных полях (при Ha = 100 или N <  1) с ростом числа Гартмана подавляется турбулентный перенос и течение ламинаризуется. Ламинаризация наблюдается вплоть до фронта струи, где течение вследствие неустойчивости переходит в турбулентное. В то же время возникающая электромагнитная сила препятствует расширению струи, поэтому снижение скорости струи сдвигается на большие расстояния вниз по потоку, и эффективная длина струи возрастает.

При дальнейшем увеличении числа Гартмана (числа Стюарта N >  1.0) развивается новая неустойчивость, связанная с проявлением «вращения» или «закрутки» струи, а ось вращения при этом совпадает с направлением основного течения (см. Рис. 14 в , г ). Вращение образуется из-за поперечных деформаций профиля скорости, вызванных интенсивными вторичными течениями, генерируемыми в области фронта струи, которые приводят к возникновению локальных областей с закруткой потока и усиливаются в продольном магнитном поле (см., например, Рис. 15 и 17). Развитие возмущений, провоцирующих вращение струи, неоднородно во времени: наблюдается чередование («перемежаемость») режимов с существенно отличающейся амплитудой флуктуаций скорости, при этом средний период вращения составляет ~1.6 c.u. и не зависит от числа Гартмана, а азимутальная скорость увеличивается с ростом числа Гартмана и достигает ~12% от средней скорости потока ( U ₀ ) в широкой части трубы при (Рис. 18). Физически похожий механизм, приводящий к радиальным колебаниям профиля скорости струи, был обнаружен в работе [11], в которой рассматривалось истечение круглой струи в квадратный канал при числе Рейнольдса, меньшем на порядок, чем в настоящей работе. Деформацию струи в [11] вызывало попеременное радиальное сжатие и растяжение потока на различных участках по длине канала, и она сопровождалась продольными низкочастотными волнами. В рассматриваемых же здесь условиях аналогичные колебания также обнаружены (см. Рис. 14 а , б ), но они затухают. В связи с этим предполагаем, что здесь, во-первых, играет роль число Стюарта, которое опять-таки на порядок меньше, а во-вторых, важны геометрические особенности: у квадратного канала в [11], есть углы, создающие «естественные» условия для несимметрии вторичных течений и индуцированных токов, а значит, больше потенциальных возможностей для пространственного распространения деформаций профиля струи. Тем не менее, влияние на течение увеличения числа Стюарта, как в рассматриваемом случае круглого канала, или увеличения числа Рейнольдса, как в [11] с квадратным каналом, может стать целью будущих исследований.

Вычисления проведены с использованием ресурсов Межведомственного Суперкомпьютерного Центра РАН (г. Москва).

Исследования выполнены при финансовой поддержке РНФ (проект № 20-69-46067).