Динамика зажатой капли в поле трансляционных вибраций

Изучению поведения включений (капель, пузырьков, частиц) в жидкости и способам манипулирования ими в настоящее время уделяется пристальное внимание [1–18]. Это вызвано интересом не только с позиции фундаментальности проблемы, но и с точки зрения приложений, где такие объекты взаимодействуют. Так, пузырьки, капли или частицы могут появляться или исчезать в процессе изменения состояния системы, например, при разрушении слоя и пленки жидкости [19–21], при кипении и испарении [22, 23], при конденсации [24] и другом. Особую роль в таких процессах играет растекание жидкости по поверхности раздела, то есть движение линии контакта сред [25–35].

В большинстве процитированных работ предполагается, что линия контакта смещается равномерно, что жидкость растекается либо под действием стационарного внешнего поля (силы тяжести, температуры и другого), либо за счет межмолекулярных взаимодействий (в частности, ван-дер-ваальсового притяжения). При этом заметную роль играет молекулярная вязкость. Вследствие этого существенно ограничивается использование подобных моделей при быстропеременном движении линии контакта. В работе [36] при изучении волн на деформируемой горизонтальной поверхности жидкости между двумя вертикальными стенками, для периодического перемещения линии контакта вдоль вертикальной стенки, предложено следующее условие:

∂ζ _* ^* =Λ ^* k ⋅ ∇ ζ ^*. ∂ t

Здесь: ζ ^* — отклонение горизонтальной поверхности от равновесного положения; t ^* — время; Λ ^* — феноменологическая постоянная (параметр смачивания или параметр Хокинга); k — вектор нормали к твердой поверхности; далее краевым углом называется угол, образуемый вертикальной стенкой и горизонтальной поверхностью (в состоянии равновесия он предполагается прямым). В результате параметр смачивания Λ ^* , который имеет размерность скорости, характеризует степень взаимодействия контактной линии с вертикальной стенкой, а все сложные процессы, происходящие в непосредственной близости от линии контакта, из рассмотрения исключаются. Граничное условие (1) включает два важных предельных состояния: фиксированное положение контактной линии при ∂ζ ^* ∂ t ^* = 0 [9, 37, 38] и фиксированное значение краевого угла k ⋅ ∇ ζ ^* = 0 [9, 39, 40]. Во всех других случаях оно описывает затухание свободных колебаний, которое связано с взаимодействием линии контакта с твердой вертикальной стенкой при движении.

Условие (1) и его модификации (с учетом гистерезиса краевого угла [41], электросмачивания [42], неоднородности поверхностей [43]) использовались, например, при изучении собственных и вынужденных колебаний полусферической капли [44, 45], пузырька на подложке [46, 47], колебаний цилиндрической капли [48–50], пузырька, окруженного жидкостью конечного объема [51, 52], рассеивания капиллярных волн [53], движения линии контакта по вертикальной поверхности [54, 55]. В работе [42] на основе (1) предложена модель колебаний капли между разными поверхностями в переменном электрическом поле. Затем эта модель использовалась для описания осесимметричных колебаний капли [49] и объемных колебаний пузырька [51]. Собственные трансляционные колебания такой капли между одинаковыми поверхностями исследовались в работах [48, 56], вынужденные — в [48]. В данной работе изучаются трансляционные колебания зажатой капли жидкости, аналогичные [48], но между разными поверхностями, подобно [49]. Основное внимание уделяется влиянию различающихся свойств поверхности. Влияние других параметров задачи подробно изучено в вышеперечисленных работах.

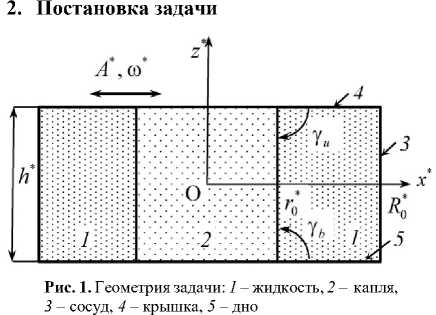
Рассмотрим колебания капли жидкости плотностью **

ρ _i и вязкостью ν _i в сосуде цилиндрической формы высотой h ^* и радиусом R ₀^* , заполненном другой *

жидкостью, характеризуемой плотностью ρ _e и вязкостью ν ^* _e (Рис. 1). Система координат O x ^* y ^* z ^* связана с сосудом. В состоянии механического равновесия капля имеет форму кругового цилиндра высотой h ^* и радиусом r ₀^* , ось O z ^* совпадает с осью симметрии цилиндра. Размеры сосуда возьмем достаточно большими, по сравнению с размерами капли

( r0* << R0*), чтобы пренебречь влиянием боковой стенки сосуда на поведение капли. На сосуд действует внешняя вибрационная сила с амплитудой A* и частотой ω* , направленная перпендикулярно оси симметрии капли и вдоль оси Ox* .

Предположим, что жидкости несжимаемые и невязкие, то есть выполняются следующие условия для частоты вибраций: ω ^* r ₀ ^* <<  c_i ^* _{, e} и ν ^* _{i , e} << ω ^* r ₀^*2 ( c_i ^* _{, e} — скорость звука в жидкости). Например, для капли воды ( c_i ^* = 1,5 ⋅ 10³ м/с, ν ^* _i = 10 ^{- 6} м²/с) радиусом r ₀^*~ 10 ^{- 2} м в воздухе ( c_e ^* = 3,4 ⋅ 10² м/с, ν ^* _e = 10 ^{- 5} м²/с) диапазон допустимых частот ω ^* ~ 10 ^-1 ...10 ⁴ рад/с. Это позволяет вместо вектора скорости v ^* ввести потенциал скорости ϕ ^* : v ^* = ∇ ϕ ^*.

При движении линий контакта выполняется граничное условие (1). Параметр смачивания для каждой поверхности индивидуален: Λ ^* _u — на «верхней» крышке сосуда ( z ^* = h ^* I 2 ), Λ ^* _b — на «нижней» ( z ^* = - h ^* 2). Благодаря этому условию диссипацию энергии можно учитывать даже при использовании приближения невязкой жидкости [36, 41–56]. Это позволяет, согласно теореме Кельвина о циркуляции, рассматривать течение как потенциальное при наличии деформируемой поверхности раздела.

На деформируемой боковой поверхности капли, которая является поверхностью раздела двух жидкостей, зададим постоянный коэффициент поверхностного натяжения σ* . Эта поверхность в цилиндрических координатах (r , a, z ) определяется как r = r0 + Z (a , z , t ), где Z (a , z , t ) — функция, описывающая отклонение цилиндрической поверхности от равновесного положения, t* — время. Силой тяжести можно пренебречь в случае сильного поверхностного натяжения, малых размеров капли и близких плотностей жидкостей, то есть должно быть малым число Бонда (Этвеша): Bo = g*r0*2 |р* -р*|/ст* << 1, где g* — ускорение свободного падения.

Выберем в качестве единиц измерения: координат — r ₀^* (по горизонтали) и h ^* (по вертикали);

отклонения от положения равновесия поверхности раздела жидкостей — A * ; плотности — р * + р * ;

* **2

времени —Jl p e + р_t ) r ₀ /ст ; скорости — A кст /л( р e + р i ) r ₀ ; давления — A ст / r ₀ .

Исследуем только малоамплитудные колебания капли: A <<  r ₀ . Запишем линеаризованные уравнения и граничные условия в безразмерном виде в неинерциальной системе отсчета, связанной с сосудом:

ЛФ к =0,     Рк =-р k      -®2 re™ t cos а|     (к = *, e), k 5t

r = 1: 5ф е = 5ф1- . d2Z ,2d2Z Ре - Pi z++ b -y, da     дz dZ = 5ф (3) 5 r 5 r , 51 5 r ’ r ^ да :     ф е ^ 0 , (4) z = ±1:    ^ = 0, 2      5z (5) r = 1, 1       5Z        ,5Z z = ±— :   — = +Л b—, 2         51       u, b 5z (6) где Pi, ф, и pe, фe — давление и потенциал скорости в капле и в окружающей жидкости соответственно.

Краевая задача (2)-(6) включает семь безразмерных параметров: геометрический параметр — b = rjh ;

отношения плотности

**

р / =р / /(р е +р , ) и р е = р е /(р е +P _i ) ; амплитуду S = A/r, и частоту

* / *       * X                                  ~                                                                               Л К * и * . * X * / *

ю = юл (р е +р , ) r /ст вибраций; параметры смачивания крышки X и = Л _м J(p _е +р_t ) r /ст    и дна

х ь=льь V (ре+р*) r>* /ст*.

• 3.    Собственные колебания

Рассмотрим лишь собственные трансляционные колебания капли, так как внешняя сила, входящая в уравнение Бернулли (2), возбуждает только трансляционную моду. Решение краевой задачи (2)–(6) без учета внешней силы в уравнении (2) представим в виде рядов Фурье по собственным функциям оператора Лапласа при граничных условиях (4) и (5):

ф , ( r , a , z , t ) = Re I i Q ^ ( ( a 0 _n R ^l_0n ( r ) cos ( 2 n n z ) + a 1 _n R in ( r ) sin ( ( 2 n + 1 ) n z ) ) cos ( a ) ) e i " t k n =0

”

фe (r,a,z,t) = Rei iQ^((b0nR0n (r)cos (2nnz) + b1 nКЩ (r)sin ((2n + 1)nz)) cos (a))e "t I, k к=0                                                                                 ' J да

^Z ( ^z , t ) = ^R e I I ^ ( c 0 n k k n =0

cos ( 2 n n z ) + c 1 _n sin ( ( 2 n + 1 ) n z ) ) + d 1 z + d ₂ z ² I cos ( a ) e^{1 n} t I ,

^R 00 ( ^r ) = ^r ,      ^R 0 n ( r ) = 1 1 ( ^{2 n nbr} ) ,      ^R 1 in ( ^r ) = 1 1 ( ( ² n ⁺ 1 ) ^{n br} ) ,

R0e0 ( r ) = r-1,    R0en ( r ) = K1 ( 2Пnbr ) ,    Ren ( r ) = K1 (( 2n + 1)Пbr ) , где a0n, a1 n, b0n, b1 n, c0n, c1 n, d1 и d2 — неизвестные постоянные амплитуды, 11 (r) и K 1 (r) — модифицированные функции Бесселя первого порядка 1-го и 2-го рода соответственно, Q — частота собственных колебаний. В решениях (7)–(9) первые слагаемые под знаком суммы описывают четные гармоники (относительно смены знака координаты z ), вторые слагаемые — нечетные гармоники. Общий вид решения (9) определяется граничным условием баланса нормальных напряжений (3), и тогда два последних слагаемых в (9) будут отвечать нечетным и четным гармоникам соответственно.

Следующая задача на собственные значения Q получается после подстановки решений (7)-(9)

в однородную краевую задачу (2)–(6):

EO - 2^ и .. b )( E + O ) -Q 2 = 0 ,

где

e=1 - 2bl+

6 Q ²

со

Q2 £

n =1

( - 1 ) n C n

Q 0 n -Q ²

n

C = ±—^L n 22 n n

^{( n} >  1 ) ,

1          -

O = - + Q2 2

( - 1 ) n S n

Q 2 n -Q ²

4 n ² n ² b ¹

n Rin (1) „  Rin (1)

R 0 nr ( 1 )    ^P e R inr ( 1 )

^{( n} >  1 ) ,

( 2 n + 1 ) 2 n ² b ²

p Rin!1!-p Ra1! ‘ Rinr (1)       R1enr (1)

( k >  0 ) ,

Rnr (r ) =

dRn( r) dr

( k = i , e ; l = 0,1),

при этом Q _{0 n} и Q 1 _n — частоты четных и нечетных гармоник трансляционной моды собственных колебаний цилиндрической капли со свободной линией контакта ( X ^ о ) [39, 56].

Алгебраическое уравнение (10) имеет комплексные решения Q , то есть свободные колебания затухают. Диссипация энергии свободных колебаний связана с взаимодействием линии контакта с крышкой/дном сосуда. Отметим, что при закрепленной ( X ^ 0) или свободной ( X ^ о ) линии контакта на одной из горизонтальных плоскостей в системе происходит диссипация энергии. Например, для закрепленной или свободной контактной линии на дне и конечных значениях X _и уравнение (10) принимает вид:

X b = 0:

^X ь ^ ^{о :}

EO = bu. ( e + о), 2Q v     ’ i (E + O) + bX^ = 0.

При одинаковых смачивающих свойствах крышки и дна сосуда X _и = X _b =X уравнение (10) представляет собой произведение двух множителей, каждое из которых является частным уравнением для нахождения частот четных или нечетных мод:

| E -X ib || O -X ib | = 0 . (11)

I q)1 qJ

Эти уравнения совпадают с аналогичными уравнениями в [48, 56] и подобны уравнениям в [42, 46, 49].

На рисунке 2 показаны частоты Re ( Q ) и декременты затухания Im ( Q ) основной гармоники свободных колебаний. При одинаковых X частота обращается в нуль после некоторого критического значения параметра смачивания (Рис. 2 а ). Критическое значение соответствует точке ветвления кривой декремента (Рис. 2 б ). Данный эффект связан со степенью взаимодействия линии контакта с поверхностью крышки/дна: при малых значениях X это взаимодействие велико, и возможны «изгибные» колебания капли, которые описываются основной гармоникой трансляционной моды [48, 56]. С увеличением значения X взаимодействие с зажимающими плоскостями уменьшается, и капля при движении сохраняет свою цилиндрическую форму аналогично капле со сводной линией контакта (постоянным краевым углом) [39].

При различающихся параметрах смачивания (Xи ^ Xb) «изгибные» колебания могут не исчезать, если один из параметров достаточно мал. На рисунке 2а показано, что частота основной гармоники отлична от нуля на всем интервале значений Xu при малых и конечных Xb , тогда как при больших Xb зависимости Re (Q0) (Рис. 2а) и Im(Q0) (Рис. 2в) качественно совпадают с аналогичными графиками для случая одинаково смачиваемых пластин.

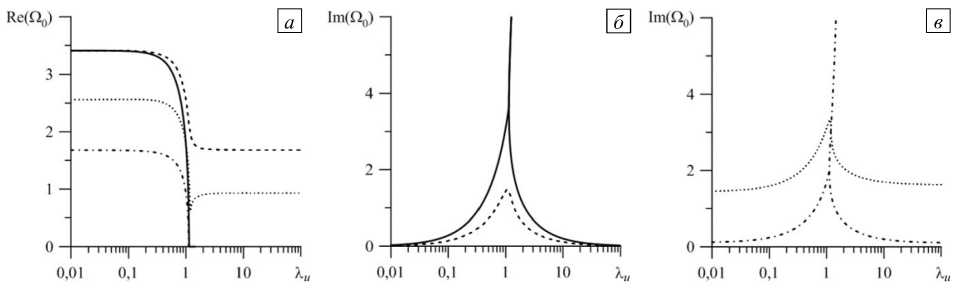
Рис. 2. Частота ( а ) и декремент затухания ( б , в ) основной гармоники трансляционной моды при b = 1, р i = 0,7 и разных значениях X _b : X u - сплошная линия, 0 - штриховая, 1 - пунктирная, 10 - штрихпунктирная

Частоты более высоких гармоник монотонно убывают с увеличением параметра смачивания (Рис. 3 а ). Декременты затухания (Рис. 3 б , в ) имеют максимумы при конечных значениях X . В целом все зависимости качественно совпадают со случаем пластин с одинаковыми свойствами. Отметим, что наибольшую частоту имеет капля с закрепленной линией контакта, а наименьшую — капля со свободной контактной линией. Вместе с номером гармоники растет и декремент.

С увеличением геометрического параметра b частоты колебаний тоже увеличиваются. На рисунке 4 показаны зависимости основной гармоники для двух значений b . Видно, что критический уровень параметра смачивания не зависит от b .

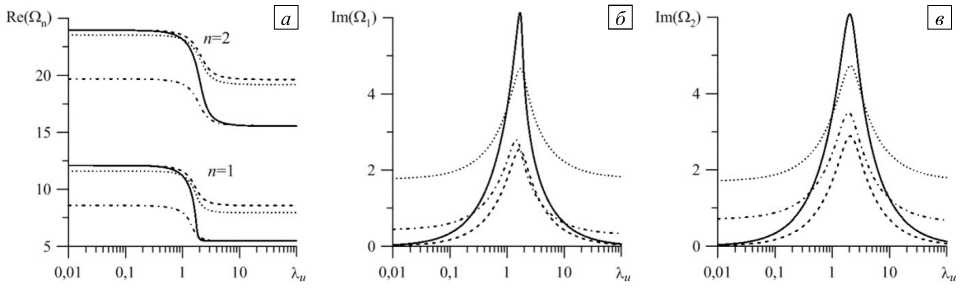
Рис. 3. Частота (а) и декремент затухания (б, в) двух гармоник трансляционной моды при b = 1, рi = 0,7 и разных

значениях X _b : X u - сплошная линия, 0 - штриховая, 1 - пунктирная, 10 - штрихпунктирная

Рис. 4. Частота (а) и декремент затухания (б, в) при рi = 0,7 и разных значениях b и X b : Xu - сплошная линия,

0 – штриховая, 1 – пунктирная, 10 – штрихпунктирная

• 4.    Вынужденные колебания

При исследовании вынужденных колебаний решение полной краевой задачи (2)–(6) находится в виде,

аналогичном (7)–(9):

Ф, ( r, a, z, t ) = Re I i юД( a 0 n R0 n (r) cos (2 nnz) + a1 n Rin (r) sin ((2 n + 1)nz)) cos (a)) e'“ t I,(12)

X n=0

(,„.)

Фe (r, a, z, t) = Re I i®^((b0nR0n (r)cos (2nnz) + b1 nRln (r)sin ((2n + 1)nz))cos (a))e   I,(13)

V k=0X                                                                               7

((^/

Z( z, t ) = Re 2j(c0»c°s (2 nnz) + Cn sin ((2 n + 1)nz)) + dxz + d2z 2 cos (a) e    .(14)

VVn=0x "                                                         77

Подставляя решения (12)–(14) в задачу (2)–(6), получаем выражения для неизвестных амплитуд:

E u - » = ¹

_d = ⁽Р , -^—Р e ⁾⁽ E u ^— E b )

¹ ub bu

d ₂ =

—

^{( P} i ^—P e ^{)( O}u ^{+ O}b )

E u O b + E b O u   ’

2C +„ 2 у MX to ² n z1 Q 2 n -to ²

₊ b^ i to

^Ou ,

1 _{+ ю}² У ⁽ 1 ) S n ₊ b ^XX

,

2 n =o Q 1 _n — to       i to

^R 0 nr ^{( 1 )}         L            ^R 1 nr ^{( 1 )                      1}     /      ,      ,1 \                      ¹     /     , C ,1 \

, b n = a 1 n^m ,    a on = /л ш⁽ c 0 n ⁺ Cd 2 ) , a n = m⁽ c n ⁺ S n^d 1 )

^R 0 nr ^{( 1 )                    R} 1 nr ^{( 1 )                R} 0 nr ^{( 1 )                                 R} 1 nr ^{( 1 )}

, x ( 1   2 b ² V              to ² C_n d 2               to ² S_n d 1

c 00 = ^(p i ^{— P} e ^{) —} I 7X⁺   2 I ^d 2 ,      c 0 n = q2      2 ,      ^C 1 n = q2     2 ^.

V 12 to j             ^ _{0 n} —го           ^ 1 _n —ю

Из выражений (15) видно, что все амплитуды пропорциональны множителю ( р i —р _e ) , то есть при одинаковых плотностях капли и окружающей жидкости система будет двигаться как целое, без каких-либо колебаний капли. В общем случае все амплитуды являются комплексными числами, за исключением предельных случаев (закрепленных линий контакта и постоянных краевых углах).

Для удобства демонстрации результатов и их обсуждения введем следующие обозначения: Z u =|С ( 0;0,5;0)| — амплитуда колебаний линии контакта на крышке; Z _b =|С ( 0; — 0,5; 0)| — на дне; Z ₀ =|Z ( 0;0;0)| — в центре сосуда; Z q =|Z ( 0; 0,25; 0)| — при z = 0,25; у u ( у _b ) — краевой угол между крышкой (дном) и цилиндрической поверхностью капли (см. Рис. 1).

На рисунке 5 показаны зависимости амплитуды колебаний от частоты вибраций ю для трех значений X _b при фиксированном значении параметра смачивания крышки X u = 1. Отметим, что максимальные значения амплитуды колебаний достигаются в случае линейного резонанса. Резонансный пик на основной частоте собственных колебаний отсутствует при больших значениях X (Рис. 5 а , г ), так как эта частота обращается в нуль (Рис. 2 а ). Кроме этого, существуют «антирезонансные» частоты, при которых линия контакта неподвижна при любых величинах X (Рис. 5 б , д ). Значения этих частот удовлетворяют условиям:

d 1 = 0 ,

d ₂ =

Р i ^—Р e

,

^{16 — 2 b} /to ^+ю ^ ^{( —} 1 ) C n /(Q q n ^— to )

n =1

то есть такие частоты определяются четными гармониками. При достаточной подвижности линии контакта появляются дополнительные «антирезонансные» частоты и на нечетных гармониках (Рис. 5 б , сплошная линия), но они зависят от соотношения параметров Хокинга.

Внешняя сила возбуждает только четные гармоники (подробнее см. в [48]), поэтому при одинаковых значениях параметра Хокинга X имеется только один резонансный пик на частоте четной гармоники, который располагается между двумя соседними значениями «антирезонасных» частот (Рис. 5 б , д ). В случае различающихся X _u и X _b дополнительно к ним возбуждаются нечетные гармоники, что приводит к появлению резонансных пиков на частотах и этих гармоник. Эти пики наиболее заметны при значениях X таких, при которых взаимодействие еще довольно сильное, но линии контакта уже подвижны. Однако в большинстве случаев резонансная амплитуда четных гармоник больше, чем нечетных, то есть основная часть энергии передается четным гармоникам. Амплитуда краевого угла меняется в больших пределах (Рис. 5 в , е ), но уменьшается с увеличением X вследствие снижения взаимодействия между линией контакта и твердой поверхностью.

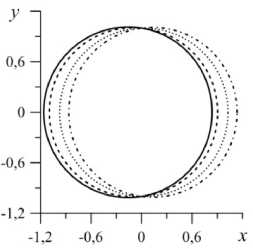
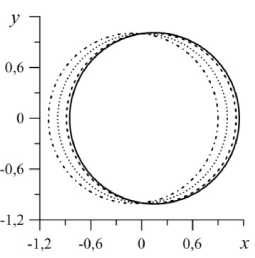
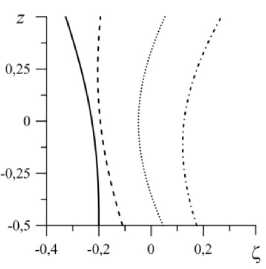
На рисунке 6 показаны динамические формы контактных линий и профиль боковой поверхности капли жидкости в разные моменты периода колебаний T и значения краевых углов на протяжении всего периода.

Капля смещается вдоль направления вибраций (Рис. 6 а , б ) согласно решению (12)–(14). Амплитуда колебаний боковой поверхности капли (Рис. 6 в ) мала, так как основная частота собственных колебаний при данных параметрах равняется нулю. Профиль боковой поверхности капли такой, что может быть описан четной функцией. Из рисунка 6 г следует, что при больших значениях X (при слабом взаимодействии между линией контакта и дном сосуда, Рис. 1) амплитуда краевого угла уменьшается.

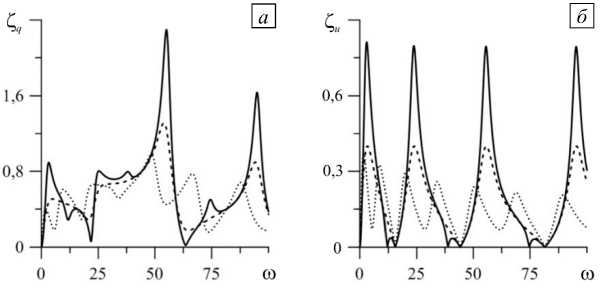
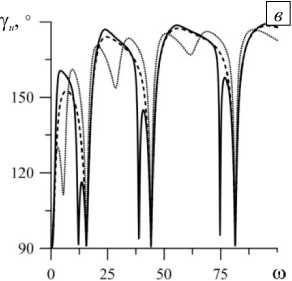
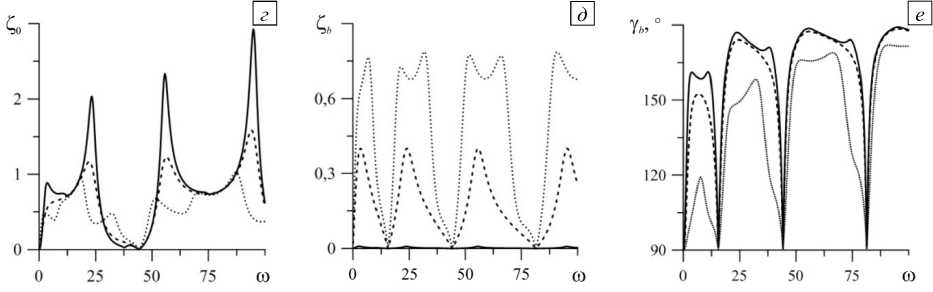
Рис. 5. Зависимость амплитуды колебаний боковой поверхности ( а , г ), линии контакта ( б , д ) и краевого угла ( в , е ) от частоты внешних вибраций го при р i = 0,7 , X u = 1 и разных значениях X b : 0,01 - сплошная линия, 1 - штриховая, 10 - пунктирная

б

в

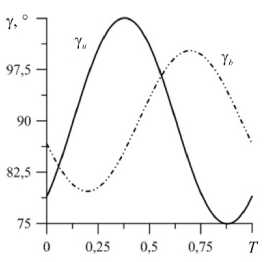
Рис. 6. Форма линии контакта 1 + 0,5 Z ( z , t ) при разных z : 0,5 ( а ) и -0,5 ( б ), форма боковой поверхности капли при а = 0 ( в )

в различные моменты периода колебаний капли t : 0 – сплошная линия, 0,125 T – штриховая, 0, 25 T – пунктирная, 0,375 T – штрихпунктирная; на фрагменте ( г ) представлены изменения краевых углов в течение всего периода колебаний

• 5.    Заключение

Исследованы собственные и вынужденные колебания капли жидкости, зажатой между двумя параллельными твердыми поверхностями с различающими свойствами, под действием трансляционных вибраций. Граничное условие, налагаемое на контактную линию, приводит к затуханию колебаний, что позволяет использовать потенциальное течение с деформированной поверхностью раздела, согласно теореме Кельвина о циркуляции, в модели невязкой жидкости.

Параметры Хокинга для каждой плоскости отличаются между собой, что проводит к появлению в спектре как четных гармоник трансляционной моды, так и нечетных. Внешнее вибрационное воздействие возбуждает только четные гармоники, но из-за взаимодействия линий контакта с поверхностями, имеющими разные свойства, нарушается симметрия относительно середины капли, и появляются нечетные гармоники. Резонансная амплитуда на частотах четных гармоник больше, чем на нечетных. Следовательно, большая часть энергии содержится в четных колебаниях формы капли.

В случае ограничивающих поверхностей с одинаковыми свойствами основная частота трансляционной моды обращается в нуль после некоторого критического значения параметра Хокинга (подробнее см. в [48, 56]). При разнородных поверхностях эта частота не обнуляется в широком диапазоне значений параметров смачивания и монотонно убывает с увеличением одного параметра при фиксированном другом. При нулевой частоте отсутствует соответствующий резонансный пик, что хорошо заметно на построенных амплитудночастотных зависимостях. Таким образом, полученные результаты могут быть использованы, например, при определении гладкости поверхности и измерении интегрального параметра взаимодействия — параметра Хокинга.

Работа выполнена при финансовой поддержке Министерства науки и высшего образования РФ (бюджетная тема № 121031700169-1) (собственные колебания) и гранта РФФИ (проект № 20-31-90104) (вынужденные колебания).

P. 417-435.

Vol. 275. P. 285-299.

P. 442-467.