Динамика жидкости в подвижном сосуде с наклонными решетками

Одним из ключевых приложений задач динамики сосудов, частично заполненных жидкостью, является разработка эффективного демпфера вибраций различных конструкций: высотных зданий, нефтяных платформ. В качестве такого эффективного демпфера могут использоваться резервуары, частично заполненные жидкостью, с частотой собственных колебаний жидкости, согласующейся с собственной частотой колебания конструкции (TLD – Tuned Liquid Damper). При этом жидкость воздействует на конструкцию с силой, находящейся в противофазе к внешней нагрузке [1]. Для интенсификации диссипативных процессов в жидкости в сосуде располагают вертикальные решетки [2, 3]. Кроме того, решетки могут быть использованы как управляемый элемент системы TLD, при помощи которого можно изменять свойства демпфера, подстраивая его под внешние условия. Одним из таких механизмов управления служит изменение угла наклона решеток, что приводит к изменению структуры потока в резервуаре и, следовательно, к изменению собственной частоты системы и сопротивления решеток.

В представленной работе рассматриваются гармонические колебания сосуда с двумя решетками, частично заполненного жидкостью. Проводится сравнение различных моделей турбулентности на точность расчета коэффициента потерь давления. На основе численного моделирования уравнений Навье–Стокса исследуется влияние угла наклона решеток на коэффициент потерь давления при различных значениях амплитуды колебания сосуда и длин пластин решеток. Влияние угла наклона решеток на диссипативные свойства было ранее исследовано аналитически [4]. В работе [4] на основе модели потенциального течения жидкости с учетом потерь давления потока при протекании через решетки получены распределения диссипации энергии системы от частоты колебаний сосуда. Причем, как будет показано в представленной работе, используемая в работе [4] аналитическая зависимость коэффициента потерь давления от угла наклона решеток нуждается в уточнении.

Постановка задачи

Пусть сосуд прямоугольной формы, частично заполненный жидкостью до уровня h , колеблется вдоль горизонтальной оси по гармоническому закону:

x _s = A sin( ft ), где А – амплитуда колебаний, f – частота колебаний, t – время . Симметрично вертикальной оси в сосуде расположены две решетки, отклоненные от вертикали на угол ± φ (рис. 1). Расстояние между решетками обозначим как L 1 при длине дна сосуда, равной L .

Значения параметров задачи выбраны в соответствии с работой [2]: L = 0,966 м, L 1 = 0,2 L , h =

0,119 м. Введенные на рис. 1 параметры решеток взяты следующими: b s = 0,001 м , d e = 0,005, 0,01, 0,02 м, d s подобран таким образом, чтобы «сплошность» решеток S n была фиксирована S n = d s /( d s + d e ) = 0,42. Угол наклона решеток варьировался: 40° ≤ φ ≤ 90°. Частота колебаний соответствовала резонансной частоте малых колебаний данного сосуда без решеток: f = 3,4585 с^–1. Амплитуда колебаний изменялась: A = 0,0025, 0,005, 0,01 м. Теплофизические свойства жидкости соответствовали воде ( µ ж = 10^–3 Па·с, ρ ж = 1 000 кг/м³), газа – воздуху ( µ г = 1,48·10^–5 Па·с, ρ г = 1 кг/м³).

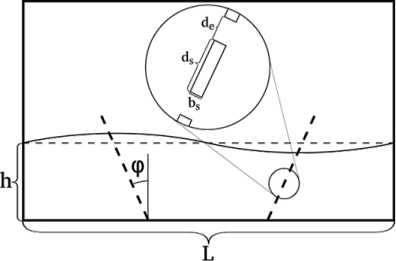
Рис. 1. Схема сосуда с решетками

Математическое описание

Наличие вставок в сосуде приводит к возникновению вихревого течения. В случае размеще- ния в колеблющемся сосуде решеток за ними образуются разномасштабные вихревые структуры (рис. 2), что может привести к турбулизации течения жидкости. На рис. 3 показано распределение кинематической турбулентной вязкости в области около решеток и между решетками при колебании сосуда. Расчеты кинематической турбулентной вязкости показывают, что при заданных параметрах колебаний сосуда в области между решетками развиваются пульсации, генерируемые решетками. Данный факт говорит о необходимости проведения расчетов в турбулентном приближении.

Моделирование турбулентного движения системы двух несжимаемых жидкостей в подвижном сосуде проводится при помощи осредненных по Рейнольдсу уравнений Навье– Стокса совместно с SST k - ω -моделью, записанных в неинерциальной системе отсчета. Для моделирования границы раздела фаз жидкость-газ используется метод объема жидкости (VOF) [5]. Система уравнений имеет

Рис. 2. Линии тока в области около решетки: темный цвет – газ, светлый – жидкость

вид:

Рис. 3. Распределение турбулентной вязкости

∇⋅ v = 0, р + Vpv v = -V p + v ( ⁽ p + P t ) V v ) - p x s i + p g . da ^v _{V!    A}

+ v ∇ α = 0,

_{µ =}      ρ a ₁ k

• ^t max( a ₁ ω , 2 S_tF ₂)

  
  

  P + Vp Vk = V ^f ( p + ^P ) V k ^ + P k - в p k o ,

  
  

  V ^C

  
  
  
  

  p _{+ V}pV o = V f ( p + ^P ) Vo ^ + C

  
  

  V     ^C o    7

  
  

  ^;a ^P_k - c e P^¹ + 2(1 - fo^ ^p V k V O). k ω

  
  
  
  

  Здесь v – поле вектора осредненной скорости, p – поле давления, i , j – единичные векторы в направлении осей x и y , g – ускорение свободного падения, α – маркерная функция, принимающая значения от 0 до 1 (причем 0 соответствует газу, 1 – жидкости), k – поле кинетической энергии турбулентности, ω – поле удельной скорости диссипации энергии, ρ, µ – плотность и динамическая вязкость, пересчитываемые следующим образом:

  ρ = ρ _ж α + ρ _г (1 - α ), µ = µ _ж α + µ _г (1 - α ) .

  Модельные функции и константы определены следующим образом:

  
  
  
  

  S t = 2S t ⋅ S t ,

  
  

  S t = 2 ( ^{V V} +^{V V} T ) , F 2 = tanhC Y l ), Y 2 = max ²

  
  

  kk 500 Pp в tod ’ d² to ,

  
  

  ^,

  
  
₁ 4.         .           kk 500 p/ p 4 pc2 .n k

в = 0,09, P k = min( P k , с_х в k o ), P k = P t I 2S_t - ^( V - v )E J V v ,

C α = F 1 C α 1 + (1 - F 1 ) C α 2

C β = F 1 C β 1 + (1 - F 1 ) C β 2 ,

C ?k = F 1 ^ k 1 ^{+ (1 -} F 1 ⁾ ^ k 2

F 1 = ^tanh^{( Y} i ), ^Y = min max -^.^^ ,^-22 ,

V V                 ^o J      k^o^

CD_{k ω} = max(2 ρσ_{ω 2} 1 ∇ k ⋅ ∇ ω ,10 ^{- 10} ), a ₁ = 0,31, c ₁ = 10, ω

C α 1 = 0,5532,C β 1 = 0,075, σ k 1 = 2, σ ω 1 = 2, C α 2 = 0,4403,C β 2 = 0,0828, σ k 2 = 1, σ ω 2 = 1,186, d – расстояние от расчетной точки до ближайшей твердой стенки, E – единичная матрица.

В качестве граничных условий на границах решеток для k , ω и осредненной скорости течения жидкости задавались нулевые значения, на границах полости для k и ω использовались пристеночные функции [6], для осредненной скорости течения жидкости задавались условия прилипания.

В данной модели пренебрегаем влиянием сил поверхностного натяжения, что оправдано применением на практике сосудов больших размеров.

Процедура численного решения

Для решения системы уравнений (1)–(6) использовался открытый пакет OpenFoam [6]. Особенностью реализации метода VOF в пакете OpenFoam является использование в уравнении переноса маркерной функции (3) искусственного конвективного члена vr. , уменьшающего толщину переходного слоя между фазами [5]:

^ + V (vra) + V (vra(1 - a)) = 0. d t

Расчеты проводились на двумерной сетке, содержащей 140 000 ячеек. В основной области по-

тока строилась неструктурированная треугольная сетка, а вокруг каждой пластины структурированная прямоугольная, обеспечивающая разрешение вязкого подслоя (рис. 4). Для совместного решения уравнений для давления и импульса использовался алгоритм PISO-SIMPLE. Для аппроксимации конвективных членов уравнений движения и турбулентных характеристик использовалась схема вверх по потоку, для уравнения переноса маркера – схема SuperBee. Для решения системы линейных уравнений использовался метод сопряженных градиентов с предобуславливателем. Для поиска предобуславливающей матрицы использовался обобщенный многосеточный метод. Шаг по времени выбирался так, чтобы число Куранта не превосходило 0,5.

Рис. 4. Пример расчетной сетки в области око ло пластины при φ = π/6

Ci

x

Верификация модели

Для апробации выбранной модели турбулент-

7-

ности и расчетной сетки была проведена серия

расчетов с вертикальными решетками. На рис. 5

- о X

показана зависимость осредненного коэффициента потерь давления C l от числа Келегана– Карпентера KC [7]:

5~8

Cl =

^^^^e

о 2n

Fco^-d e P U m d s

3-

k x x ®8 ‘ЧсА

A°6

X

где F – сила, действующая на решетку со стороны Z fL жидкости, 9 = ft, Um = ПЬ sin (0,5n(1-L1 /L)), Z —

2-

<Ш

^ %

X

_i_________i_________i_________i_________ KC

20    40    60    80    100

амплитуда колебания свободной поверхности.

Число Келегана-Карпентера: KC =

2 n U_m fd s

Как видно из данного рисунка, результаты, полученные при помощи SST k-ω модели турбулентности хорошо, согласуются с экспериментом, что говорит о достоверности результатов, полу-

Рис. 5. Зависимость коэффициента потерь давления от числа Келегана-Карпентера; 1 – экспериментальные данные, 2 – SST k-ω модель турбулентности, 3 – k-ε модель турбулентности

Ct

9 г1

8-

o

ченных в статье.

7-

о

O A = 0.0025 X A = 0.005 ▲ A = 0.01

Результаты расчетов

В результате проведенных расчетов была получена зависимость коэффициента потерь давления от угла наклона решеток при различных значениях амплитуды колебаний. На рис. 6 изображена зависимость коэффициента потерь давления от угла наклона решеток при d e = 0,01 м. Как видно из рисунка, данная зависимость имеет локальный максимум, зависящий от амплитуды колебаний сосуда. Данный факт свидетельствует о том, что при заданной амплитуде существует угол на-

6-

5"

4"

3-

2-

o

o

o

"1 L__________I__________I_________I__________I__________I__________I_________I_________I__________I__________I__________I_________I_________I__________I__________I__________I_________I__________I__________I__________I__________I_________I_________I__________I__________I__________I_________I__________L

0  10 20 30 40 50

Рис. 6. Зависимость коэффициента потерь давления от угла наклона решеток при различных значениях амплитуды колебаний

клона, когда диссипация энергии колебаний жидкости наибольшая ( φ max ≈ 20° при А = 0,0025 м, φ max ≈ 15° при А = 0,005 м). Однако при A = 0,01 м локальный максимум не наблюдается, что может быть связано с характерными значениями числа Келегана–Карпентера: 21 <  KC < 35 при А = 0,0025 м, 34 <  KC < 70 при A = 0,005 м и 60 <  KC < 100 при A = 0,01 м.

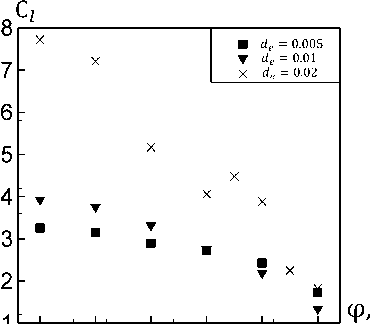
На рис. 7 изображена зависимость коэффициента потерь давления от угла наклона при A = 0,01 м и различных длин пластин решеток: d e = 0,005, 0,01, 0,02 м. При этом число Келегана– Карпентера принимает следующие значения: 126 <  KC < 150 при d e = 0,005 м, 22 <  KC < 40 при d e = 0,02 м. Видно, что при малых значениях числа KC (при d e = 0,02 м) в зависимости C l от угла наклона также наблюдается локальный максимум.

—I I I I I I I I I I I I I I I I I I I I I I I I I I L

0   10 20 30 40 50

Рис. 7. Зависимость коэффициента потерь давления от угла наклона решеток при A = 0,01 м и различных значениях de

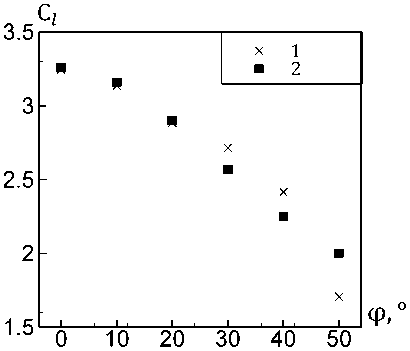
Рис. 8. Зависимость коэффициента потерь давления от угла наклона решеток при A = 0,01 м; de =0,005 м;

1 – численное решение, 2 – аналитическое

В работе [8] на основе экспериментальных данных по измерению отклонения потока при стационарном протекании через наклонную решетку получено аналитическое выражение для зависимости коэффициента потерь давления от угла наклона:

C i = ((V C * + 1 ) i* - 1 ] ,                                (7)

где ψ – угол отклонения потока от нормали к решетке, значение которого были найдены из эксперимента [4, 8].

Авторы [4] применяют данную зависимость для случая колебательного движения сосуда при больших значениях числа KC ( KC > 40). На рис. 8 показано изменение коэффициента потерь давления при увеличении угла наклона для случая A = 0,01 м и d e =0,005 м (126 <  KC < 150). Из данного рисунка видно, что при малых углах наклона наблюдается хорошее согласование значений C l , полученных по формуле (7) и расчетных значений. При больших углах наклона решеток расчетные значения отличаются от значений C l , полученных по формуле (7). Кроме того, формула (7) не применима при малых значениях числа Келегана–Карпентера, что говорит о необходимости ее уточнения для случая периодического течения жидкости через решетки при широком диапазоне значений числа Келегана–Карпентера и угла наклона решеток.

Заключение

В результате проведенных расчетов задачи колебания прямоугольного сосуда, частично заполненного жидкостью и имеющего вставки в виде наклонных решеток, были получены коэффициенты потерь давления при различных значениях параметров: угла наклона решеток, амплитуды колебания сосуда, длины пластин решеток. На основе анализа полученных значений коэффициентов потерь давления можно сделать следующие выводы:

• •    при малых значениях числа Келегана-Карпентера зависимость коэффициента потерь давления от угла наклона имеет локальный максимум. Угол, при котором достигается локальный максимум, зависит как от амплитуды колебаний, так и от геометрических параметров решеток;

• •    зависимость коэффициента потерь давления от угла наклона, используемая в литературе, требует уточнения для случая больших углов наклона решеток и малых значений числа Келегана–Карпентера.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-31-00068 мол_а.