Динамика зубчато-рычажных механизмов на основе эллиптических колес

Качество продукции и повышение производительности труда достигается в результате автоматизации производства. В связи с этим широкое применение в технике имеют машины-автоматы.

Подача обрабатываемого материала в рабочую зону машины-автоматы осуществляется различными транспортно-загрузочными устройствами. Эти устройства основаны на механизмах, преобразующих непрерывное движение в движение с остановками (выстоями). К таким относятся храповые, мальтийские, зубчатые с неполным числом зубьев и другие механизмы.

В храповых механизмах движение ведомому звену сообщает собачка, зацепляющаяся с ним при движении в одном направлении и выходящая из зацепления при движении в обратном направлении. Главный недостаток храповых механизмов заключается в том, что в начале и конце фазы движения имеют место удары [1].

Значительно большее распространение по сравнению с храповыми получили мальтийские механизмы, обеспечивающие более благоприятные кинематические характеристики. Выходное звено мальтийского механизма выполняется в виде диска или стола, на котором расположено несколько пазов. В паз может входить палец, расположенный на ведущем кривошипе. К недостаткам мальтийских механизмов относят наличие ударов в начале движения [2].

В зубчатых механизмах с неполным числом зубьев вращение ведомого звена, имеющего зубья по всей окружности, будет происходить в пределах некоторого угла, соответствующего зацеплению его с ведущим зубчатым колесом, имеющим зубья не на всей окружности. Недостатком зубчатых механизмов с неполным числом зубьев является наличие удара в моменты начала зацепления [2].

Таким образом, основным недостатком вышеперечисленных механизмов является разрыв кинематической цепи на время остановки с последующим ее замыканием на время движения, что приводит к жестким ударам, вследствие чего возникают большие динамические нагрузки на детали механизма периодического движения (МПД), приводящие к их быстрому износу.

Существуют другие МПД, которые обеспечивают остановку без разрыва кинематической цепи. Это комбинированные механизмы, в которых рычажные системы и системы круглых зубчатых колес включены параллельно, причем звенья рычажного механизма несут на себе оси зубчатых колес таким образом, что, по крайней мере, одно из них движется вместе с шатуном. Такие механизмы получили название зубчато-рычажные [1].

Исследования зубчато-рычажных механизмов (ЗРМ) на основе круглых зубчатых колес показали их ограниченные кинематические возможности [3].

Использование в зубчато-рычажных механизмах периодического движения (ЗРМПД) некруглых зубчатых колес [4] позволяет существенным образом расширить их кинематические возможности.

На рис. 1 представлена схема зубчато-рычажного механизма на основе эллиптических зубчатых колес. Устройство представляет собой совокупность рычажного кривошипнокоромыслового механизма, ведущее (кривошип 1) и ведомое (коромысло 3) звенья которого шарнирно соединены с шатуном 2 и основанием 4, и передаточного зубчатого механизма для передачи вращения от кривошипа 1 на ведомый вал (на рис. 1 не показан), расположенный соосно с шарниром Оз, соединяющим коромысло 3 с основанием 4.

Передаточный зубчатый механизм выполнен в виде зацепляющихся между собой эллиптических зубчатых колес 5, б, 7 и 8, смонтированных на звеньях рычажного механизма. Колесо 5 и кривошип 1 жестко закреплены между собой таким образом, что колесо 5 вращается относительно центра 01 вместе с кривошипом. Колеса 5 и 7 имеют возможность поворота и установки под углами 5] и У2 (регулируемое угловое смещение большой полуоси некруглых колес относительно шатуна и коромысла рычажного механизма при расположении на одной прямой кривошипа и шатуна в крайнем правом положении рычажного механизма).

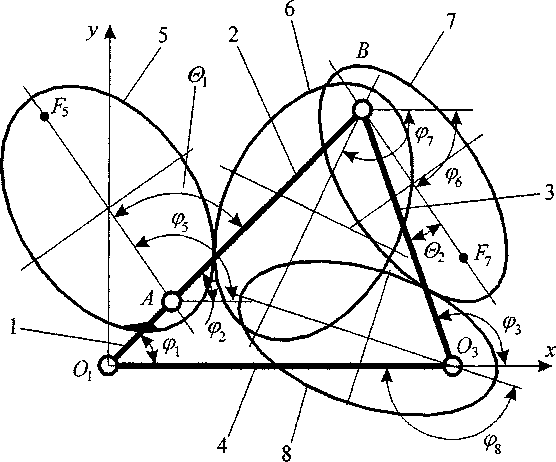
Рис. 1. Схема зубчато-рычажного механизма с эллиптическими зубчатыми колесами

Математическая модель данного механизма, позволяющая определить функцию положения ведомого колеса

^=/(^i)>                                                          (О получена из рассмотрения схемы, показанной на рис. 1.

Параметры, определяющие положения шатуна 2 (угол поворота ф₂) и коромысла 3 (угол поворота ф₃) в зависимости от угла поворота кривошипа ф_х, легко определить из соотношений базового четырехзвенного механизма [1].

Угол поворота эллипса 5 с учетом монтажных углов определяется следующим образом:

ф5 = фх + 6Х.

Угол поворота эллипса б можно определить из выражения

Фь = Фз + arcsm -— -----------г • sin ф. ,

<1-2^ СО8ф5 + 6])

где е_х - эксцентриситет (отношение фокусного расстояния АРз к длине большей оси эллипса) зубчатых колес 5 и б.

Угол поворота эллипса 7 находим из выражения

(Р7 = arcsin

_v2e_x cos 5, -е² -1

+arccos

/ /     7 \2    2 j2

yd + b) + c — d

4   2(a + 6)c

c² + d² -(a + bV

-arccos------------^z—У₇ + led         ²

где a = O_XA, b = AB, с = ОД , d = BO₂.

И, наконец, положение ведомого звена определяет угол поворота эллипса 8: . (      \-е²        .    )

% = arcsin —--------rsmp7 + р3 ,

V1 - 1е_г cos ф_п + е_г )

где е2 - эксцентриситет зубчатых колес 7 и 8.

Ввиду большого числа параметров механизма и сложного вида функции (1) применялся метод оптимизационного синтеза [2]. В процессе многопараметрического поиска было просчитано 50 000 наборов параметров зубчато-рычажных механизмов на основе эллиптических колес и были выбраны два механизма, обеспечивающие наибольшие остановки выходного звена при допустимой точности позиционирования ^^йои=0,5°.

На рис. 2 представлена зависимость угла поворота выходного звена ф^ от угла поворота входного звена ф_х , полученная аналитическим расчетом на ЭВМ, для двух выбранных механизмов, в сравнении с механизмом, обеспечивающим максимальный выстой среди ЗРМ с круглыми колесами.

Из рисунка видно, что зубчато-рычажные механизмы на основе эллиптических зубчатых колес обеспечивают более продолжительную остановку выходного звена, чем зубчато-рычажные механизмы, основанные на круглых зубчатых колесах.

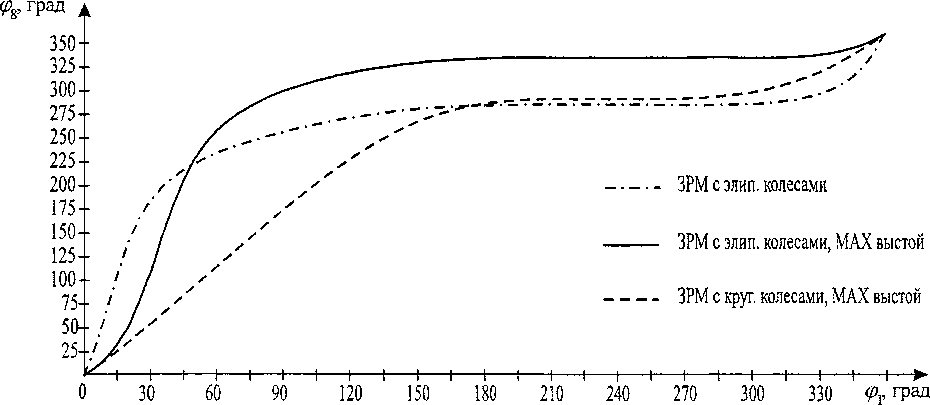
Рис. 2. Г рафик зависимости угла поворота выходного звена от угла поворота входного звена для исследуемых механизмов

Путем графического дифференцирования были получены графики зависимости угловой скорости ы₈ выходного звена от угла поворота ф_х входного звена (рис. 3).

Для оценки динамического момента воспользуемся следующим выражением:

^дин ⁼ ^пр " ^Е% ’                                                                                       (6)

где £_% - угловое ускорение выходного звена механизма, J - приведенный момент инерции зубчато-рычажного механизма.

Приведенный момент инерции зубчато-рычажного механизма на основе эллиптических колес определяем из выражения

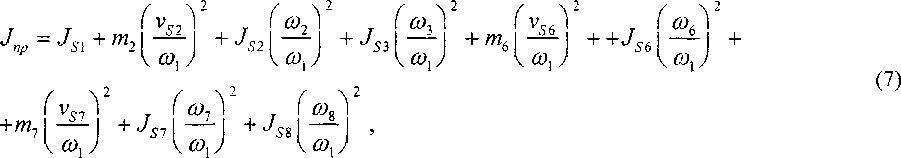
где звеном приведения принято входное звено; т\-т% - массы звеньев механизма; Js\-Js% ~ моменты инерции звеньев относительно центров тяжести; v_sl-v$₈ - скорости центров тяжести звеньев; 0)_х - со_& - угловые скорости звеньев.

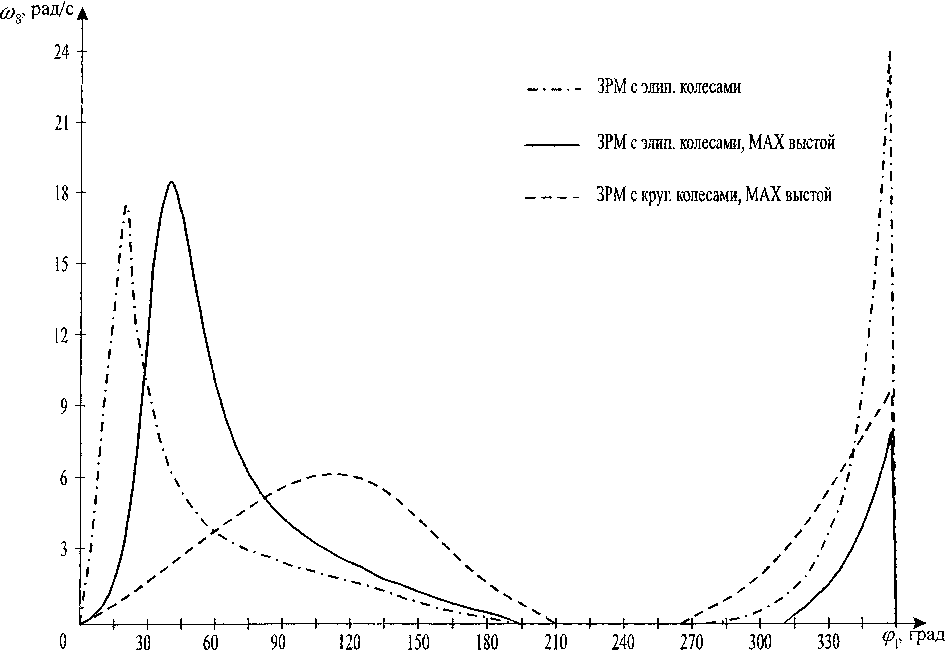
Рис. 3. График зависимости угловой скорости выходного звена от угла поворота входного звена для исследуемых механизмов.

Результаты расчета приведенного момента инерции для зубчато-рычажного механизма на основе эллиптических колес, обеспечивающего максимальный выстой выходного звена, занесены в таблицу.

Значения приведенного момента инерции ЗРМ

Фх	15°	35°	45°
J«p	10,4	31,3	18,1

60°	75°	330°	345°
6,6	6,1	5	5,3

Угловое ускорение ^ выходного звена механизма часто является определяющим при оценке динамического момента. Для его определения необходимо дифференцировать полученные ранее зависимости угловой скорости <У₈ выходного звена от угла поворота ф_х входного звена. Графики зависимости углового ускорения £₈ выходного звена от угла поворота ф_х входного звена показаны на рис. 4.

Анализ графиков зависимости углового ускорения 5_g выходного звена механизма от угла поворота ф_х входного звена показал, что ЗРМ с эллиптическими колесами имеют большие ускорения по сравнению с ЗРМ на основе круглых зубчатых колес. При этом максимальный выстой зубчато-рычажного механизма на основе эллиптических колес может быть обеспечен с меньшим угловым ускорением, а следовательно и с меньшими динамическими нагрузками, по сравнению с другим зубчато-рычажным механизмом на основе эллиптических колес.

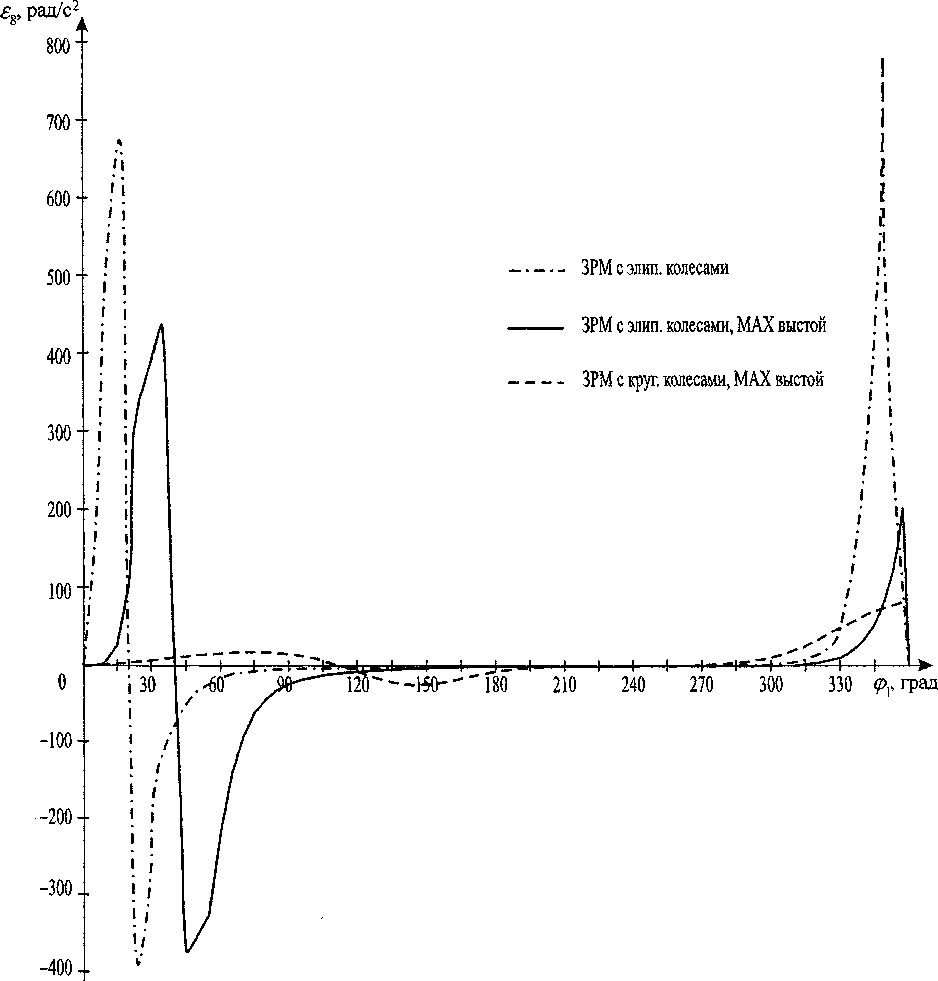
Рис. 4. График зависимости углового ускорения выходного звена от угла поворота входного звена для исследуемых механизмов

Анализ параметров двух рассматриваемых ЗРМ с эллиптическими зубчатыми колесами показал, что чем больше эксцентриситет эллиптических колес 7 и 8, тем больше угловое ускорение £g выходного звена механизма.

Далее, используя выражение (6), был рассчитан динамический момент для ЗРМ с максимальным выстоем (рис. 5).

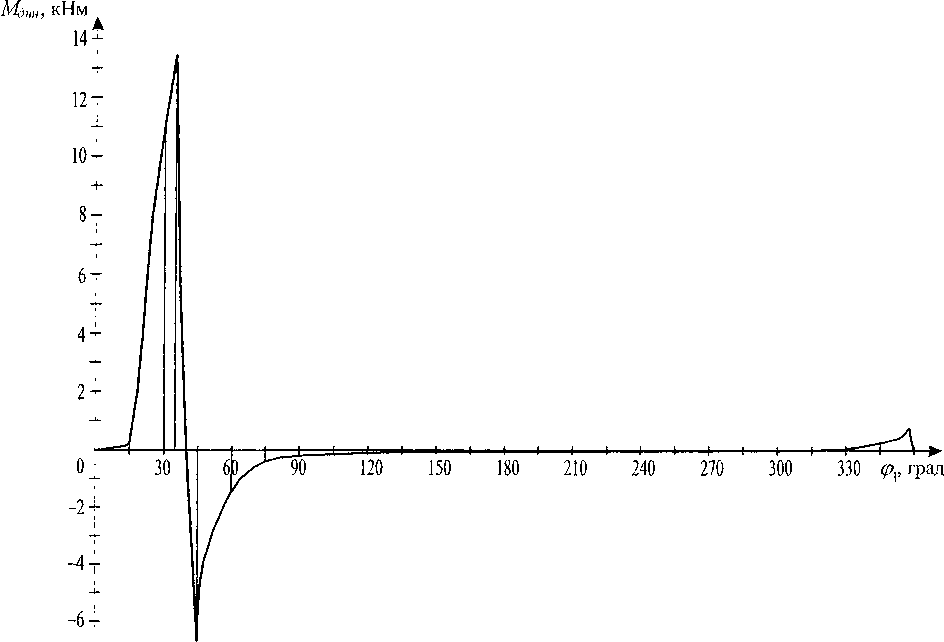
Рис. 5. Зависимость динамического момента от угла поворота входного звена зубчато-рычажного механизма на основе эллиптических колес, обеспечивающего максимальный выстой выходного звена

Выводы:

• 1.    Зубчато-рычажные механизмы обеспечивают остановку без разрыва кинематической цепи, вследствие чего не происходит жестких ударов.

• 2.    Зубчато-рычажные механизмы на основе эллиптических колес обеспечивают более чем в два раза больший выстой выходного звена по сравнению с зубчато-рычажными механизмами на основе круглых колес.

• 3.    Угловые ускорения выходного звена зубчато-рычажного механизма с эллиптическими колесами превышают угловые ускорения выходного звена зубчато-рычажного механизма с круглыми колесами.

• 4.    В зубчато-рычажном механизме с некруглыми колесами с увеличением эксцентриситета эллиптических зубчатых колес ухудшаются динамические характеристики, поэтому с целью улучшения динамических показателей необходимо уменьшать эксцентриситет эллиптических зубчатых колес, образующих выходную пару зацепления в механизме.