Discrete model of paired relay-race

Corporative-concurrent systems, in which corporative part is represented by the team, which must overcome some distance, and concurrency is the natural environment of their existence, are widespread in manifold fields of human activity, such as economics, politics, defense, sport, etc. [1-4].

Below paired relay race is considered [5, 6], in which two teams, A and B, participate. Team A adheres the active strategy and has a rigid schedule of passing the distance, divided onto stages. Also team A watch the team B, which from the point of view of team A passes its stages during occasional time interval, may overcome the stage on one of possible routes, which team В can select randomly too. The cost of the relay race depends not only on common winning or loosing the relay-race as a whole, but on winning and loosing the stages. So the team, which passes at current time a stage with a lower number, pays the team, which is situated at the time at a stage with higher number, the forfeit, which depends on the time, until the stage inequality persists.

The analytical model of such a system, based on the semi-Markov processes theory [7-10], adopt little to computer interpretation due to extremely high computational complexity of the calculation both current functional states of the system, and the sum of forfeit, which a winner receives from a loser. To reduce complexity it is necessary to work out a special approach, oriented onto the algorithmic realization. Such approaches are currently known insufficiently, that explains the necessity and relevance of the investigations in this domain.

1 . Model of Active and Passive Team Paired Relay Race

Structure of paired relay race under consideration is shown on Fig. 1 [5, 6].

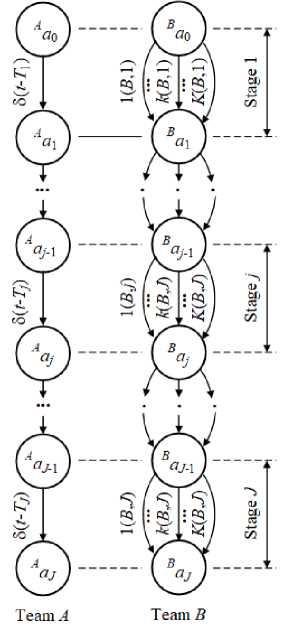
Fig. 1. Relay-races with alternative routes of the partner

On the Fig. 1:

• •    nodes { A a ₁ , ..., A a j , ..., A a J - ₁} of graph "Tearn A" and { ^Ba ₁ , ..., ^Ba j , ..., ^Ba J - ₁} of graph "Team B" simulate relay points of the distance;

• •    nocles A a ₀ and ^Ba ₀ simulate starting points;

• •    nocles A a_J and ^B a J simulate end points of the distance.

The next assumption when modelling relay race was made:

• •    two teams, А and B, participate in relay race;

• •    relay race unfolds in real physical time T

• •    the distances are divided into J stages;

• •    participants of team А passes their stages in the time, predetermined with a rigid schedule;

• •    time intervals of passing j(d)-th stage, 1 < j ( A ) < j ( B ) by a participant from team A are expressed with determinate, nonrandom values, and densities of these intervals are performed with Dirac 5 -functions 5 (t — T j ( A )), where T j ( A ) is the time of passing j -th stage by a participant from the team A;

• •    7-th stage of В team includes K(B, j) routes;

• •    time intervals of passing к IB. j). 1(B. 7) < к IB. 7) < K(B. jk 1 <  7 < J. route by team В participants are random ones and are determined with the accuracy to density fk ( B,j ) ( t ):

e after finishing of (j-l)-th stage by the (j-l)-th participant from team В j-th participant may select one of K(B, j) possible routes of j-th stage with probability p k ( B,; ),

K ( B,j )

52 p k ( B'j ) = ^1;

k ( BJ )=1

• e both teams, A and B, start their distances at once;

• e after completion of j-th stage by the previous participant the next participant starts (У I 1 ^-th stage without a lag;

• e winning or losing of a stage competition is understood as the completion of the stage the first or not the first;

e the winner’s forfeit is distributed in time and depends on the difference of stages, which the winner and loser pass.

The model of the paired relay race may be performed as two-parallel semi-Markov process [7-10]

A h ⁽ t ) = [ A h j ( A ) ,l ( A ) ⁽ t )] ,                                       Ш

B h ⁽ t ) = [ B h j ( B ) ,1 ( B ) ⁽ t )] ,                                          (2)

where A h ( t ). B h ( t ) are semi-Markov matrices of size ( J + 1) x ( J + 1).

A                  J ⁵ tt - T j ( A )) , when¹ < j ⁽ A ) < J ⁽ A ) and l ⁽ A )= j ⁽ A ) ,

h ( A ) - _u ( A ) ( t ) = | о Otherwise ,

B h ; ( B ) - 1 ,i ( B ) ⁽ t ) = |

h ; ( B ) ( t ) , when 1 < j ( B ) < J ( B ) and l ( B ) = j ( B ) , 0 otherwise ,

^Bh j ( B ) ( ^t ) = [ ^h 1( B,j ) ⁽ t ) , •••, h k ( B,; ) ⁽ t ) , •••, ^h K ( B,; ) ⁽ t )] , ¹ < j ⁽ B ) < J ^{( B} ) , (T

• ⁵ (t ^- Tj (A)) is the Dirac function; T;(A) is the rigid time of overcoming j(A)-th stage by j-th participant of the A; hk(B,;) (t) = pk(B,;) ■ f_k(B,;) (t) is the weighted time density of overcoming k (B, j)-th route by j-th participant of team В.

2.    Discrete Model

The summation of weighted densities hk ( B,; ) ( t ) gives the time density of the residence of team В participant at stage ЦВ), when passing along any rout:

к ( B,; )=1 f ; ( B ) ( ^t ) ⁼             h k ( B,; ) ( ^t ) ^•

k ( B,; )=1

Recursive procedures of the analysis of the relay race and the evaluation of the sum of forfeit is too complicated [5, 6] and unsuitable for cybernation, so simplification of the procedure is cpiite an actual task.

Let us represent time density (6) as a histogram [11, 12]. For this purpose let us divide domain 0 < T ; ( B )min <  arg [ f ; ( B ) ( t )] < T ; ( B )max < ro. where T ; ( B )min is the lower boundary of the domain, T ; ( B ) _min is the upper boundary of the domain, onto intervals ^T fc(B,; ) - 1 < t < ^T k(B,; ), ¹ < k ^{( B,j} ) < K ⁽ B,j ), ¹ < j <  J, as it is shown in Fig. 2.

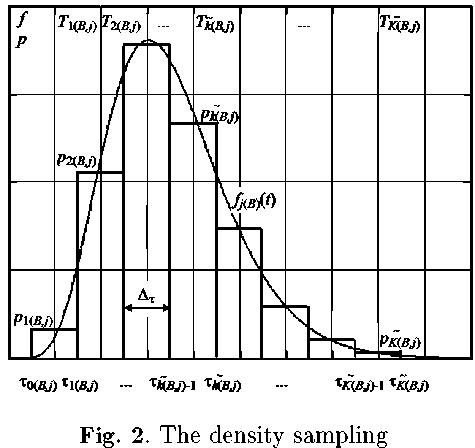
For the definition of histogram digit parameters it is necessary to set up an accuracy e of the histogram sampling. The value of e may be calculated as follows:

^{T 0(} B-j )                    K( Bj )    ^T'^k( B-j )

J  f j ( B ) ⁽ t ) dt + ^ J

0                         k ⁽ B, ^j )=1 T k ( B-j ) _ 1

f j ( B ) ⁽ t ) ^- pHB,j )

∞

dt + /

^t k ( B-j)

f j ( B ) ( t ) dt,

where t^B j)- 1 and t^B j) are the left and right boundaries of k (B,j)-th, 1 < k (B,j) < K (B, j), histogram digit, correspondingly, тЦB,j) = T0(B,j) + k (B,j) • AT, д = TK(Bj) - T0(Bj)

^T K ( B,j )     ■

The values of histogram digits p^B j ) are calculated as follows:

' ^T i( B-j )

J f j ( B ) ( t ) dt, when k ( B, j ) = 1 ,

^T k( B-j )

p-_k( Bj _} = <     J   f j ( B ) ⁽ t ) ^dt, ^when2 < k ^{( B,j} ) < K ^{( B,j} ) ^{- 1} ,

^T k( B-j ) - 1

∞ f fj(B) (t) dt, when k (B,j) < K (B,j).

. TK(.B-j)

The density sampling task may be putted on and solved as an optimization task [13], where e ^ min is the criterion, and т 0( B,j ), t^ k ( B j ), K ( B, j ) are optimization variables.

Rigid time intervals T _k (Bj ), 1 < k ( B,j ) < K ( B,j ), represented arguments of histogram digits, may be calculated as follows:

A,    ,._.,-_._.

T' i . ( Bj ) = ^tHb j ) - 1 ⁺ ”2” , ¹ < k ⁽ B, j ) < K ⁽ B, j ) ‘

(П)

Taking into account (10) and (11), one may build up the semi-Markov discrete model of team В operation. The structure of the semi-Markov model is cpiite alike the structure, shown in the Fig. 1, except that indices к ( B,j ) of the primary model should be replaced by indices к ( B, j ) in the discrete mod el, and in common, K ( B, j ) = K ( B,j ).

Discrete operation team В model, based on semi-Markov process is as follows:

B h ⁽ t ) = [ B h j ( в ) ,i ( в ) ⁽ t )] ,                                     U-)

where

B hj (в) -1 ,i (в)

( t ) = {

h j ( в ) ( t ) , when 1 < j ( B ) < J ( B ) and l ( B ) = j ( B ) , 0 otherwise ,

^Bh j ( B ) ⁽ t ) = p l 1( B,j ) ⁵ ( t   ^T 1( B,j ) ) , ^.", ^p k ( B,j ) ⁵ t-    T ; B,j )} , ..., ^p K(B,j ) ⁵ t-   ^T _K(B,j )

,

1 < j ( B ) < J ( B ) ,                                 (14)

where 5 tt — Тц_в j^, 1 < к ( B,j ) <  A ( B,j ) are Dirac functions; Тц_в j ) are the rigid time intervals of overcoming j(B)-th stage by j(B)-th participant of team B.

3.    Formulae for Competition Analysis

Due to the reduction primary model (1) - (5) to its discrete analogue (1), (3), (12) - (14), the conception of team В operation may be considered as a rigid schedule [1417] relay-race with alternative routes, which on j(S)-th stage are occasionally selected from K ( B,j ) possible routes лvith probabilities p k ( _в j ). 1 < к ( B,j ) < K ( B,j ). after the completion [j(B)-l]-th stage. So general formulae, used in [5, 6] for working out the recursive procedure of competition and relay-races analysis should be adapted to the case under consideration, in which:

e only two teams participate in a relay-race;

e both teams operate due to rigid schedules [18, 19].

The adaptation of formulae gives the next result.

Formulae, which determine the weighted time densities of winning j-th stage of the race by team A and team B, correspondingly, when both teams start their j-th stages simultaneously are as follows: e in common case

« ( t ) = f j ( a ) ( t ) [1 — F j ( в ) ( t )] ,* g ( t ) = f j ( в ) ( t ) [1 — F j ( A ) ( t )] ,           (15)

t where F... (t) = J f... (9) d9 is the distribution function; 9 is the auxiliary argument;

e when rigid schedule

^ w ( t ) = ( ⁵ (t ^— T j ( A )) , ^{when T} j ( A ) = ^min TT₃ ( a ) , T j ( в )} ,

^A         nonsense , otherwise ,

^ w ( _t ) = ( ⁵ (t ^— T j ( в )) , ^when T j ( в ) = ^min TT₃ ( A ) , T j ( в )} , ^в         nonsense , otherwise .

Formulae, which determine probabilities of winning j-th stage of the race by team A and team B, correspondingly, are as follows:

• •    in common case

∞∞ nw (t) = j fj(a) (t) [1 - Fj(в) (t)] dt, nB (t) = j fj(в) (t) [1

^— F j ( A ) ⁽ t )] ^{dt ;}

0                                                   0

• •    when rigid schedule

  1, when Tj(a) = min {Tj(a), Tj (в)} , 0 otherwise,

  
  

  ⁿA⁽t) = |

  nw(t) = Г 1,whenTj(в) = min {Tj(A), Tj(B)} , в       [ 0 otherwise.

  
  
4.    Recursive Procedure of Evaluation of Forfeit

Formulae, which describe the time density of waiting by the winner team until the loser team finishes the stage • in common case

n (t) 7 fj (A) (e) • fj (в) (t + e) de фА^в (t) =      7                       , j Fj ( a ) ( t ) dFj (в) ( t ) 0 П (t) J fj (в) ( e ) • fj (A) (t + e ) de Фв A (t) = -----07---------------------------,                      (19) j Fj ( в) ( t ) dFj (A) ( t ) where n (t) is the Heaviside function,

, j = / 0 , when t <  0 , n^'    [ 1 , otherwise;

• when rigid schedule

Ф     ( t ) = | Ht — T j ( в ) + T j ( A )) , when T j ( A ) < T j ( в ) , А^в       [ nonsense , otherwise , ^     ( t ) = { d ( t — T j ( A ) + T j ( в )) , when T j ( в ) < T j ( A ) ,                20 в^А         nonsense , otherwise .

It is necessary to admit, that at the rigid schedules case the draw effect emerges. It is impossible in common case, when there is an infinitesimal probability of A and В teams stage passing time intervals coincidence, is cpiite real when at rigid schedule case T j ( a ) = T j ( в )•

Recursive procedure of evaluation of forfeit should be considered in the twodimensional space of functional states, shown in Fig. 3 [20].

The states   of space are formed as Cartesian product of sets

[1( A ) , ..., j ( A ) , ..., J ( A ) , J ( A ) + 1] and [1( B ) , ..., j ( B ) , ..., J ( B ) , J ( B ) + 1].

Elements of sets perform the stages, which participants of teams 4 and В overcome at the current time. There are additional elements in the sets under consideration, namely J ( A ) + 1 and J ( B ) + 1. These elements simulate states, which teams fall into after completion J-th stages of distances. The race begins from state [1(4), 1(B)] and ends at state [4(4) I 1, J(B) + 1], Wandering through the space has the character of evolution, in which after every switch one (horizontal and vertical arrows in Fig. 3) or two (diagonal arrows in Fig. 3) elements of vector [^(4), j(B)] increments by unit. Switches continue until the vector reaches the state [ J ( A ) + 1 , J ( B ) + 1].

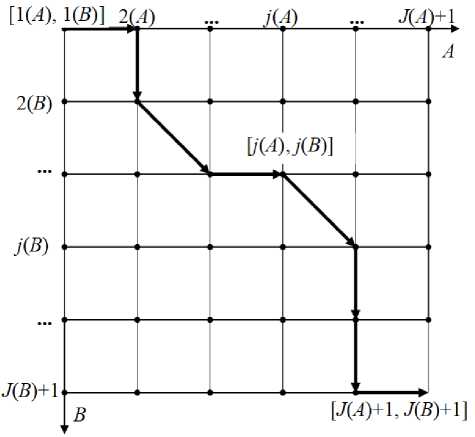
Fig. 3. The space of functional states

Time intervals of passing stage ДВ) depend on route k ( B,j ), which team В select for passing j(B)-th stage. Common number of routes selected for passing distance as a whole is equal to

J

L = H ^ ( B,j ) .                            (21)

j =1

Let us extract from all possible routes of team В route

^w

^w

s i ( B ) = k ( B, 1) , ..., k ( B,j ) , ..., k ( B,J ) ,

and evaluate the forfeit, which team A received from the team B , when evolution of team B will be developed on route (23).

For evaluation of the evolution effectiveness lets utilize quite a natural model of forfeit, defined as the distributed payment by opponent team В to gamer team A, aj(A)j(B) (t), value of which depends on time. Below the case of payment by opponent team В to garner team A, aj(A)j(B) (t), is considered. Rate of payment, aj(A)j(B) (t), is as follows:

^ i ( A ) ,j ( B ) ⁽ t )

> 0 , when i ( A ) > j ( B ) , = 0 , when i ( A ) > j ( B ) , <  0 , when i ( A ) < j ( B ) ,

where 1 < i ( A ) , j ( B ) < J + 1 .

For the evaluation of common forfeit, which team A receives from n-th team B, one can use the recursive procedure, for realization of which it is necessary to introduce the auxiliary time intervals O s ( A ), O s ( B ), where s is the number of previous switches.

When starting the competition from the initial functional state [1 ( A ) , ..., 1 ( B )] no switches is done ( s = 0). substitutions O ₀ ( A ) ^ T q A ) aiid O ₀ ( B ) ^ т 1( B ) should be made, and time intervals O ₀ ( A ), O ₀ ( B ) compete between them. А possible result of competition may be the next:

• a)    if O 0 ( A ) ₀ ( B ), then wins team A, and 00 = {O 0 ( A ) } = min {O ₀ ( A ) , O ₀ ( B ) }, O0 ^ O0 ( A ), r = 1;

• b)    if O 0 ( A ) >O ₀ ( B ), then wins team B, and 00 = {O 0 ( B ) } = min {O ₀ ( A ) , O ₀ ( B ) }, O0 ^ O0 ( B ), r = 1;

• c)    if O 0 ( A )= O 0 ( B ), then competition is in a draw, and 0 0 = {O 0 ( A ) , O 0 ( B ) } = min {O 0 ( A ) , O 0 ( B ) }, O 0 ^ O 0 ( A ) = O 0 ( B ), r = 2.

The value of forfeit is equal as follows:

θs∗ as (A, B,l) = j ai(A),i(B) (t) dt.

Substitutions for preparing the next step of recursion are as follows: • indiees of O 0 (A), O 0 (B), a nd ai (A) ,j (B) (t) should be replaced with s ^ 0 + r, i (A) =

j ( B ) =

Г i ( A ) I i ( A ) { j ( B ) I j ( B )

+ 1 in the case a) , c) , in the case a) ,

+ 1 in the case b) , c) , in the case a);

• time intervals, which will compete further should be replaced as follows

O (A) , J T2(A) in the cases a), c), s [ O0 (A) — O0 in the case b),

_{O (} B ) ^ S T 2( B ) in the cases b) , c) , ^s [ O 0 ( A ) — O 0 in the case a) .

In such a way the second compete between them.

step or recursion rigid time intervals O s ( A ) , O s ( B ) will

Let us assume that ( s = v )-th step of the recursion vector of functional state of semiMarkov process is [ i ( A ) , j ( B )], and time intervals O_v ( A ) , .O_v ( B ) compete between them. The possible result of the competition may be the next:

• a)    if O v ( A ) v ( B ), then wins team A and 0 * = {O V ( A ) } = min {O v ( A ) , O v ( B ) }, 9* _s ^ ^O V ⁽ A ), s ^ v + ¹

• b)    if O v ( A ) >O v ( B ), then wins team В and 0 * = {O V ( B ) } = min {O v ( A ) , O v ( B ) }, °* ^ ° V ⁽ B ), s ^ v + 1;

• c)    if O s ( r - 1) ( m )= O_s ( r - 1) ( n ), then competition is in a draw, 0 * = {O V ( A ) , O V ( B ) } = min {O v ( A ) , O v ( B ) }. s ^ v + 2.

The value of forfeit is calculated as follows

σ s

^θ s ^∗

( A,B,l )= /

^a i ( A ) ,j ( B ) ⁽ t ) ^dt-

Substitutions for preparing the next step of recursion are as follows: e indiees of Os (A), Os (B), should be replaced with index s ^ v + r;                                  (29)

e indiees of a i ( A ) ,j ( в ) ( t ) should be replaced in accordance with (26); e time intervals, which will compete further

O_s ( A ) ^ {

T i ( A ) in the cases a) , c) , O v ( A ) — O V in the case b) ,

O s ( B ) ^ |

T j ( _B ) in the cases b) , c) , O v ( A ) — O*_v in the case a) .

Let us assume, that the last step of recursion only team A stays in the race, and time, it spends from a previous switch till finishing 7-th stage, obtained on previous stage of recursion, is O_s ( A ) = O* . The value of forfeit on the last stage in this case is equal as follows:

a s ( A,B,l ) = J* ^aJ ( A ) - 1 ,j ( в ) ⁽ t ) dt.                            (31)

The common sum of forfeit, which team A receives from team B, is as follows a (A,B,l) = ^ as (A,B,l).                        (32)

s

The common sum of forfeit, which m-th team receives from all other teams, is as follows

L a (A,B) = ^a (A,B,l).                        (33)

i =1

It is necessary to admit, that the common sum of forfeit, a ( A, B ), team A receives from team B, depends of its own rigid schedule and distributions of time intervals (5). The only way to change sum of forfeit a ( A, B ) in a relay-race is changing team A schedule only. This is an essential obstacle, from point of view of putting and solving the forfeit optimization task.

Conclusion

In such a way in this paper proposed procedure of relay-races analysis, based on simulation of team A, as a system with a rigid schedule, and team В as a system with alternative routs of passing stages. The next step of simulation is the reducing initial semiMarkov model of team В activity to the abstraction with discrete distributions of passing stages time intervals, the task, as a whole, to analysis the concurrent system with rigid schedules of participants. This permits to work out rather simple computational procedure of the forfeit sum calculation.

Solving the problem of calculation the sum of the forfeit, which active team A gets from its opponent team B, permits to work out the optimal strategy of A team behaviour with use, f.e. game theory [21, 22]. The tactics of optimal game strategies realization is to rescheduling of passing by team A the remaining stages of distance at the expense of acceleration/deceleration its activity on the certain stages with taking into account restriction of its own resources, possible response of opponents etc.

Acknowledgements. The research was carried out within the state assignment of the Ministry of Education and Science of the Russian Federation (No 2.3121.2017/PCH).