Discussion on Damping Factor Value in PageRank Computation

Published Online September 2017 in MECS

Due to use of Internet to a greater extent, web search engines have become the most important Internet tools to retrieve relevant information. Currently, thousands of web search engines have emerge in recent years based on various ranking method [1]. Google has become one of the most popular web search engine due to its ranking method called PageRank. PageRank computation is Static computation i.e. it is computed offline for every web page and independent of search query [2, 3, 4]. These computation nature makes it popular, and it is used in many applications like inverted index reordering, selective crawling, ranking sports team, clustering of similar web pages, Bioinformatics, Network analysis, Website search engine [5, 6]. PageRank is a hyperlink structure based method that computes the rank of all web pages indexed in the Internet by the Google’s web crawler. To find PageRank one has to compute stable distribution of hyperlink matrix which is based on the web graph structure [7]. Since web contains huge amount of data so it is important that this method must be fast and needs to be accurate and efficient as much as possible [8, 9].

Langville, Brin et al, defined PageRank as the stationary distribution of a stochastic method whose states are the nodes of Web graph [7, 10]. According to them PageRank can be stated as follows: Let a random web user starts surfing from an arbitrary web page, and at every time they navigate to next web page by selecting one of the hyperlinks from the current web page. In initial approximation, we could define PageRank as the ratio of time random web surfer spent on that web page to the number of web pages visited on average. However, according to some researcher’s, this definition would not be appropriate for certain types of web pages that form a loop. Web pages in the loop may point to each other but do not point to any web page outside loop. These web pages only accumulate rank and do not distribute rank to other web pages and this property is called rank sink [8, 11, 12, 13]. To resolve rank sink issue, at every step the random web user has the choice to choose any out-link with probability a, and will restart from another node of n web pages chosen at random with probability (1 - a), where a is a damping factor [7, 14]. Brin and Page, the founders of Google web search engine, suggest to take the value of damping factor a =0.85. The reason of selection of value of a=0.85 is not clear that motivates us to perform experiment to find out the reason of dependency of a on the efficiency of PageRank. In this paper, we discuss experimental effect of damping factor on PageRank computation and suggest new value of damping factor other than 0.85 as it gives better results.

• II.    Motivation and Literature Survey

The recent survey estimated that web is the largest collection of data distributed over approximate 200 million web servers containing greater than 15 billion web pages, and larger than 600 million hosts [15, 16]. Due to dynamically growing nature of web and needs of user’s query the role of web page ranking method becomes very crucial in any information retrieval system. Today, whenever a user searches any query then search engines returns thousands or millions of results regarding query keyword. Web users do not have the much time and the patience to go through all returned pages to find the relevant one in which they are interested, and some analysis shows that the 70% web users' don’t even goes beyond the first page of SERP [17]. Therefore, it is very important for ranking method to keep the desired result within top few web pages, otherwise web search engine could be thought as improper. The PageRank method highly depends on the value of damping factor a ∈ [0,1] that plays a major role in the convergence of PageRank computation [18, 19]. However, variation in value of a not only affect rank value of web pages, but also change their displayed order in SERP [18, 19, 20]. The number of iterations taken by PageRank method grows on increasing the value of a and required more numerical precision to converge as value of a → 1. PageRank of the web graph lies between a true uniform distribution ( a = 1 ) and a meaningless artificial teleportation distribution, mostly of irrelevant web pages ( a = 0). It is easy to observe that picking small value of a is unsuitable, because too much weight provided to the identical artificial teleportation matrix [19, 21]. In this paper, we discuss the effect of different value of damping factor on computation of PageRank on various datasets.

Few researchers have discussed about effect of damping factor on PageRank computation. Chritopher Engstorm et al, observe convergence rate of PageRank computation on various damping factor value by changing the weight of some web pages in the Web graph and conclude that number of iteration taken to converge by PageRank algorithm increases as damping factor value goes closer to 1 [18]. Paolo Boldi et al, have done various analysis on PageRank computation on different damping factor value, and they observed that value of damping factor which is very closer to 1 provide true web structure and they also obtained the Maclaurin polynomial for PageRank that is independent from a and induces interesting rankings [12]. Langville et al, state that value of damping factor shows how much time random web user spent on surfing the hyperlink structure than teleporting the web [13, 22]. Guan et al, have done citation analysis of scientific research articles by using PageRank and used value of damping factor a = 0.5 and state that this value of a gives more true ranking for analysis of scientific articles [23].

In earlier years user can easily get relevant information due to small size of data on web so the value of damping factor is taken as a = 0.85 by Brin & Page, But nowadays there are more irrelevant information available on web so that random web user does not follow hyperlink structure and easily teleport to new web pages very frequently. In order to provide true link structure of web, we have to choose value of a that should be different from a = 0.85. In some applications like intraweb search engine, selective crawling, traffic analysis, bibliography ranking. The value of Damping factor a = 0.7 provides relevant ranking result same as for a = 0.85 and take less numbers of iteration and time. In this paper, we have done experiment on various datasets and observed the result for different damping factor value and concludes that a = 0.7 gives more true structure of web and take fewer numbers of iterations and time to converge the PageRank method than for a = 0.85.

The rest of paper is divided into following sections. Section II describes some mathematical terminology used in the paper. Section III includes basics of PageRank method and its computation and structure of the real Web graph. In Section IV, we discuss Improved PageRank method and the importance of Power method in PageRank computation. In Section V, we have observed the effect of damping factor on ranking of web pages as well as the convergence of PageRank Power method. In Section VI we briefly discuss about implementation details and observations. Finally Section VII concludes the experimental result.

• III.    Mathematical Terminology

We treat the HTML “points-to” relation on web pages as a directed graph, and represents it by two sets: G = (V, E) , Where V is the set of nodes corresponding to web pages, and E represents set of edges corresponding to hyperlinks between web pages. Some common mathematical definition and notations which will be used in this paper are as follows: [4, 24]

• •    Hyperlink Matrix: It shows the surfing behavior

of random surfer. The elements of hyperlink matrix are assigned by following Eq. (1):

,→

=(1)

0,ℎ

• •    Sparse Matrix : A sparse matrix is a matrix in which most of the elements are zero. By contrast, if most of the elements are nonzero, then the matrix is considered dense.

• •    Stochastic Matrix : A stochastic matrix also called transition matrix, probability matrix or markov matrix used to describe transition of markov model or random surfer. It is a matrix whose entries in each row are non-negative real numbers and sum equal to one.

• •    Aperiodic : A state i is said to be periodic with

period ≥1 if is the smallest number such that all paths starting from state back to state have a length that is multiple of . If =1 then state is not periodic. A markov model or Web graph is aperiodic if and only if all states or web pages are aperiodic.

• •    Irreducible : A Web graph is irreducible when it is

strongly connected. A directed Web graph =( ,  ) is strongly connected iff ∀ pair of nodes ( , )∈  , there is a path from to .

• •    Primitive matrix : A transition matrix is primitive matrix if it is irreducible and aperiodic .

• •    Dangling Node : A node is said to be dangling node if it does not point to any other node. In hyperlink matrix, row corresponding to dangling node contains only zero.

• •    PageRank vector (тг) : It is a column vector which contains rank value corresponding to every web page of Web graph.

• •    Dangling node vector (a): It is a binary column vector that contains One corresponding to every dangling nodes and zero for other nodes.

• •     : It is an identity column vector of 1 ∗  .

• •     : It denotes Damping factor value

• •      : Tolerance value used for convergence of

PageRank vector

• IV.    Basic PageRank Model

  The PageRank method proposed by Brin and Page in 1998, is used in Google Search engine as a basic method [7,  8]. It states that importance of web pages is

determined by the number of hyperlinks pointing to it as well as rank of those web pages which are pointing to it. It is also measured as a probability that the random web surfer visits any particular web page.

Definition 1 If web page have outlinks and one of these links pointing to another web page , then web page will pass     i.e.                importance or r ° J r ij Outdegree of Pj r rank to web page . So, PageRank of page is the sum of all the contribution made by web pages pointing to it.

Let is the set of pages pointing to then following Eq. (2) shows mathematical equation to compute PageRank:

^{= ∑ ∈                      (2)}

Where k denotes iteration number. In the beginning of iterative procedure rank of all web pages are unknown, so we assign rank of each web pages to , where n is the total number of web pages. After that this iterative equation is successively repeated and substitute the value of         in next iteration. This iterative equation begin with         = for every pages and repeated until the

PageRank score converged to some final stable values. By Eq. (2) we can compute PageRank value of web pages one at a time. Another way to compute PageRank by converting Eq. (2) in matrix format and compute PageRank vector of 1∗ , which hold rank of each web pages. Let be the hyperlink matrix of order × and is the PageRank vector at     iteration then compute

PageRank of web pages by using Power method by Eq. (3):

=                       (3)

Where M is a sparse matrix due to large number of dangling Web pages. Consider a random web surfer start surfing from any of n web pages with equal probability. Afterwards in first iteration initial vector initialize with for each web page. Subsequently after one step, the distribution vector of the random surfer will be     .

After second steps it will be      , and so on. In general, we can state that, by iterative multiplying times M to initial vector i.e.       , will give us the distribution vector of random web user after steps. This kind of nature is known as an example of Markov method or Markov matrix [14, 25]. It is clear that for any starting PageRank vector, the markov method converges to a unique stationary vector when matrix M is stochastic and primitive i.e. when the Web graph should be strongly connected and there should be no dangling web page in the Web graph [26, 27]. These two characteristics of Web graph ensures the existence of unique PageRank vector. However, it is impossible in practical scenario. Earlier, Researchers have observed the structure of Web as shown in Fig. 1 that contains basically three main components: SCC, IN-Component, Out-Component [28, 29].

First one is strongly connected component (SCC) which is the largest component in terms of size. Second, one is IN-component that contains the web pages that have outgoing links to SCC, but could not have incoming links from the SCC and the third one is Out-Component, consisting of web pages having incoming links from SCC but do not have outgoing links to reach SCC. There are other three components called Tendrils, Tubes and Isolated components which also have their importance in the Web graph structure. Tendrils are mainly two types:

One type of tendrils contains the web pages which are reachable from the IN-Component but are not having link to reach the IN-Component.

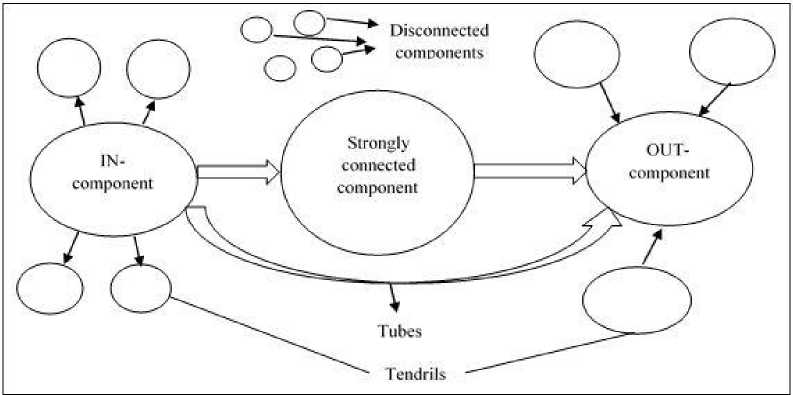
Fig.1. Structure of Web

Second type of tendrils can reach the OUT-Component, but not able to reach from the OUT-Component. Tubes contains small number of web pages that are reachable from the IN-Component and able to reach the OUT-Component, but it does not able to reach the SCC or to be reached from the SCC. Isolated components are those that are not able to reachable from the large components like SCC, IN, OUT- components, and not able to reach those components. Among these structures tendrils, OUT-Component and Isolated Component violates the rules needed for the Markov iteration method to converge to a tolerance limit value.

Consider a random web surfer that enters into OUT-Component, after that they can never leave from this component because the web pages does not have out-links to any other components. As a result, then random web user beginning in either the SCC or IN-Component are going to set-up in either the OUT component or a tendril off the IN-Component. Therefore, no web page in the SCC or IN-component winds up with any probability of a web user being there. If we take this probability as a component for measuring the importance of web page, then we determine incorrectly that nothing in the SCC or IN-Component is of any importance. Therefore, PageRank is generally improved to avoid such anomalies. There are two problems that should be avoided. First is the dangling nodes, which is a page that has no outgoing links and second is Rank Sink issue, a group of web pages that linked with each other but none of them link to any other pages.

Brin and Page have modified basic PageRank method in order to resolve above two issues [8, 30]. To solve the dangling node problem, they have used the property of stochastic matrix. They have converted hyperlink matrix M to stochastic matrix S by replacing all rows having “0” entries for every web page with ^eT . After this adjustment, any of n pages at random are visited once user reach to a dangling node [13]. This adjustment can be represented mathematically by Eq. (4):

5 = M + a( ^ ee^T) (4)

One of the problem after this adjustment is that it can’t guaranteed the convergence of the PageRank method [13, 31]. To overcome with this issue just make matrix S primitive [8, 13]. Generally, web user follow the hyperlink structure of web, at some times when they get bored then stop to follow the hyperlink structure and teleport to new web page with probability a called damping factor, by entering a new web page address in the browser’s URL. When this happened, they begin surfing again, until the next teleport required and so on. So to make primitive adjustment of matrix S, formulate a new matrix H denoted by Eq. (5) [13]:

H =aS + (1-a^e ^tT (5)

Where a denotes the damping factor and takes value 0 < a < 1.

The damping factor parameter states that how much time random web surfer follow hyperlink structures than teleporting. There are several properties of matrix H: Matrix H is stochastic, irreducible, aperiodic and primitive, and completely dense and huge, which has a bad impact on the computation of PageRank [32, 33]. Eq. (5) is a linear PageRank equation that is solved by either direct methods or iterative methods. However, direct method does not perform very well for sparse matrix as compared to iterative methods. So PageRank method solved by Power method that is one of the simplest iterative method to find the dominant eigenvalue and eigenvector of a matrix is used [4, 7, 25]. PageRank can be implemented by Power method mathematically as stated below:

Лк+1 =

(1- a ) т

^k+l =   [ aS + -------ее ]

1 П 1

^k+l =   [ a ( M + — ae^T )+ ------ee^T ]

n         n

^k+l =        +[ otn^ci + ^{(   )} e^T ]        (6)

From Eq. (6), it is clear that there is no need to store matrix S and H , only rank one component of a vector and e are needed. We know that vector matrix multiplication is 0 (n) because it contains approximation 10 nonzero per row [34]. The Power method is slowest among other iterative methods like Gauss-Seidel, Jacobi, restarted GMRES etc., but it has advantage over these methods i.e. it is a matrix free iterative method so no matrix computation is required and because of this, it is preferred while storage of the hyperlink matrix is very large.

Brin and Page, Amy N. Langville and Carl D. Meyer, Pretto, L discussed in their paper and also state that Power method needs only 50-100 iteration to converge the algorithm and as we know that each iteration of the Power method requires 0 (n) computation so it can take approximate 50 0 (n) to 100 0 (n) Power iteration [7, 13].

• VI.    Effect of Damping factor on PageRank Algorithm

As it is stated above that damping factor a shows the proportion of time the random web surfer follows the hyperlinks contrary to teleporting. So damping factor a plays an important role in PageRank computation by Power method shown in Eq. (7) [8, 25]:

^k+l =   [ aS + ^{(   )} E ]           (7)

Where E = is the teleportation matrix of n×n, a controls priority given to the hyperlink structure over artificial teleportation matrix E . Many researchers state that the value of damping factor a affect the convergence rate of PageRank Power method [11, 12, 14, 18, 19]. We have performed an experiment to observe the impact of damping factor on the convergence rate of PageRank algorithm, and ordering of web pages displayed on web search engine on various datasets by using following Eq. (8) & algorithm (1):

^k+l =  (∑ ⁿk O⁵ )+ ^{(1- )}

+ “^(∑    )

∀ . . dangling nodes    /

Where Лк+1 denotes PageRank vector at Rih iteration,

0^] represents out-degree of web-page j .

Algorithm 1 PageRank algorithm by using Power method

• 1:    procedure я₀ =          ℎ ой ()

• 2:     я₀ = (a row vector)

• 3:     н = row - normalized hyperlink matrix

• 4:     а = Damping factor value

• 5:     е = Convergence tolerance value

• 6:     п = Number of Web pages in Web graph

• 7:

• 8:do

• 9:         ^k+l =

• 10:         5=|| ^k+l ^- П_к ||

• 11:      к=+1

• 12:   while ( 6 < €)

• 13:    end procedure

• VII.    Experimental Analysis and Discussion

In this section, we have described experiments performed on various real datasets taken from cs.toronto.edu and snap.stanford.edu website. These websites contain many data sets of distinct queries [35, 36]. Subsection 1 briefly describe the data and the experimental setup and subsection 2 observe the performance of PageRank on the different value of damping factor а varies between 0 and 1.

• A.    Data and Experimental setup

We have implemented PageRank Power method in JAVA (JDK 1.8) language. We have done experiment on single Linux machine (Ubuntu 14.04 LTS), Intel Core i5 CPU 3.2 GHz, 4 GB RAM on following datasets:

Table 1. Datasets with their attributes

Dataset	No. of Web pages	No. of Dangling Web pages
YouTube dataset (D1)	1157827	783042(0.67%)
Road network dataset (D2)	1971281	6075 (0.30%)
Wikitalk dataset (D3)	2394385	2246783 (93%)

First dataset, YouTube is a video-sharing web site that contains a social web network. YouTube users can create various social groups to connect and interact with other YouTube users. Here YouTube graph represented by G ∶ ( V , E ) Where V is node & E edge of Web graph represented YouTube users & links between various users respectively. Second Dataset, A road network of California, where Intersections and endpoints of roads represents nodes and the roads connecting these intersections or road endpoints represents directed edges. Third Dataset, Wikipedia dataset shows that every registered user has a talk page, which he and other users can edit in order to communicate and discuss updates to various articles on Wikipedia. Nodes in the network represented by Wikipedia users and a directed edge from node i to node j represented by that user i at least once edited a talk page of user j .

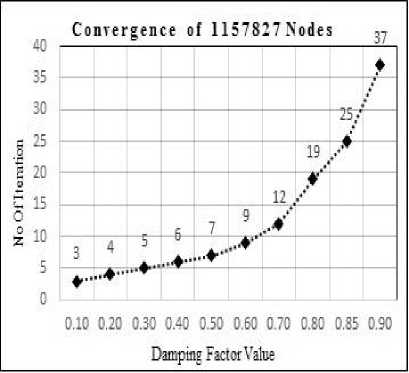
Fig.2(a)

Due to sparse matrix storage we stored these web graphs into Hash-map data structure for the computation of PageRank. Since in the PageRank computation, only nonzero entry of the hyperlink matrix is required, so we store only the non-zero entry in Hash-map data-structure that reduce not only storage but it also provides fast access of data [2, 10, 27]. For large datasets Hash-map data structure would be better in terms of accessing of the element and storage of elements than hyperlink matrix. We have implemented Hash-map data-structure in Java language using Guava library provided by Google [37].

• B.    Observation of damping factor on PageRank computation

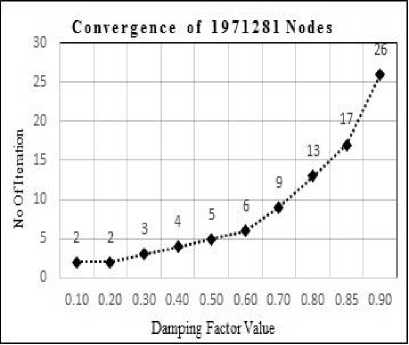
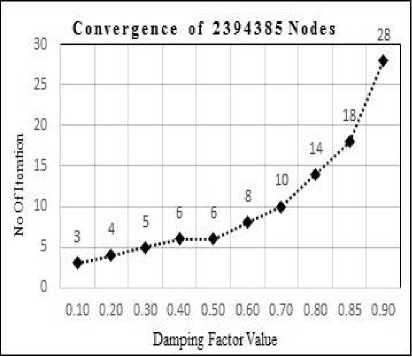
We have applied PageRank method on each dataset till convergence and observed the convergence speed for different damping factor value. Following Fig. 2 shows the number of iteration taken to converge PageRank method on various damping factor. The plotted graph depicts that as the value of damping factor increases, the number of iteration taken by PageRank method to converge also increases for tolerance value g =10 ⁷. From Fig. 2, we can say that there is slight change in the number of iteration when 0< a < 0.65 but graph curve increases rapidly when value of a > 0.65 and tends to 1 .

Fig.2(b)

• C.    Damping factor value versus Convergence Rate:

Earlier researchers have observed that value of damping factor not only controls the convergence of PageRank method but also affects the ordering of web pages returned by the PageRank method [18]. As we can see that in Fig. 2, that a =0.7 take only 12 iterations to converge when g =10 ⁷ for 1157827 nodes. As a →1 this number becomes prohibitive and for the large dataset, the choice of a → 0.85 still requires too much time to converge. Earlier Brin and Page chosen value of a = 0.85 because the large value of a gives more weight to the true link structure of web while smaller values of a

Fig.2(c)

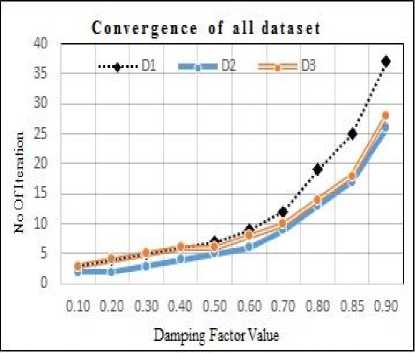
Fig.2(d)

Fig.2. Number of iteration taken to converge for the value of a = (0,1) on tolerance value e =10   . (a) For 1157827 nodes, (b) for 1971281

nodes, (c) for 2394385 nodes, (d) for all data nodes together.

increases the influence of the artificial probability vector. However, nowadays random web user does not follow hyperlink structure and teleport frequently to other web pages due to a huge amount of irrelevant data on the web. So the value of damping factor between a ∈ (0.7, 0.8) gives truer behavior of hyperlink structure, and it also takes fewer numbers of iterations to converge the method. Damping factor value a =0.7 would give more weight to artificial teleportation vector that would be useful in personalized PageRank, Domain based search engine and many other application where artificial teleportation vector plays a major role.

Fig. 2 shows the number of iteration taken by PageRank method to converge on various dataset with tolerance value g=10 7 . Number of iteration taken to converge on PageRank method does not totally depend on data size, it also depends on several properties of dataset i.e. the number of dangling nodes, connectivity of nodes. As we can see that from Fig. 2(d) and Table 1 for dataset D3 PageRank method takes fewer numbers of iterations to converge than D1.

In this experiment we have taken, only top 25 web pages return by PageRank method because SERP (Search engine result pages) contains almost 20 to 30 web pages in their first result page that are more relevant to the web user, and on average 90% users do not go beyond the first result page for any particular query [9, 11]. If any web page indexed in the top 25 position for a = 0.85 (    . )

but cannot get position in top 25 for a=0.7 (   . ), then we have taken a parameter X to show that whether page is indexed in top 25 or not, parameter X is defined as follows:

_x 0, if web page is not get position in top 25

= { _1≤Z ≤25,    wℎ en it is indexed in top 25

As example in Fig. 3(a) web page 1454 got 21 ^st position for . but it can’t got position in top 25 for

. so we give it X =0. In Fig. 3 Straight line shows the ordering of web pages for damping factor .   . In Fig

3(a, b, c) we can see that web pages for . got almost same ordering w.r.t. .   .

In Fig. 3a) only one web page could not index in top 25 i.e. Page No. 1964 , In Fig. 3b) Three web page could not index in top 25 i.e. Page No. 1259079, 737950, 749665 and In Fig. 3c) only one web page could not index in top 25 i.e. Page No. 1118838 for damping factor . w.r.t.

. on D1, D2, D3 dataset respectively.

We compare the top 25 web pages returned by . with other damping factor a value in terms of two useful and informative parameters, namely Relative Common Web pages (RCWP): It Indicates the number of web pages got the position in top 25 for both damping factor value. Second one is Web Pages got a different index w.r.t. .  ( N[): It Shows the number of web pages got a different index/order number for both damping factor value.

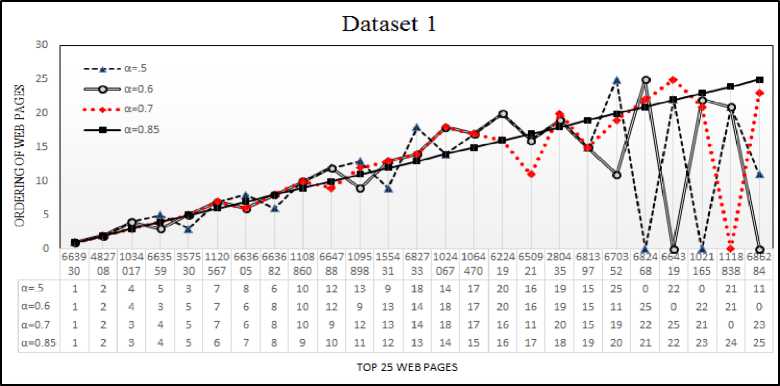
Fig.3(a)

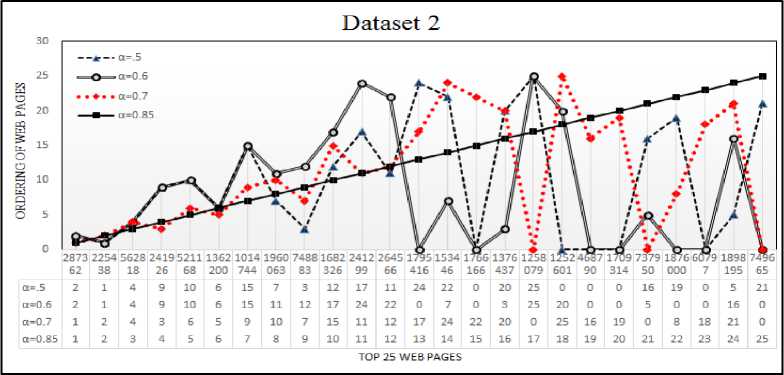
Fig.3(b)

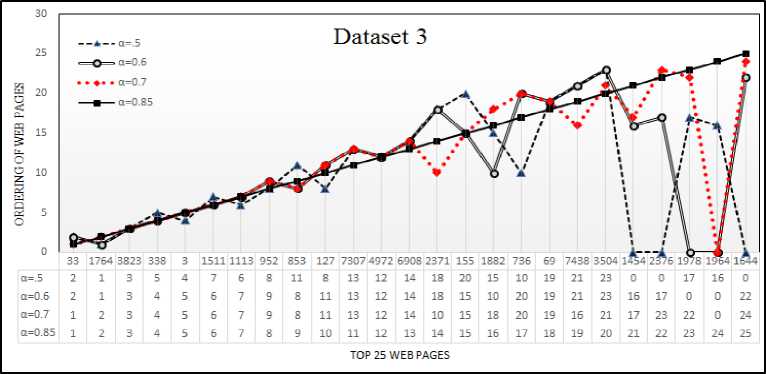
Fig.3(c)

Fig.3. This figure a, b and c, shows relative comparison of ordering number of top 25 web pages for different damping factor on D 1 , D 2 , D 3 dataset respectively.

We define the following notation and expressions used to compute these parameters:

• •    wp_a : Top 25 web pages returned by PageRank method for damping factor value a .

• •    RCWP_a : Number of common web pages for damping factor value a with respect to .   .

• •    N_a : Number of web pages got the different position for damping factor value a w.r.t. .   .

• •    WP' : Web pages on index i for damping factor value a .

Relative Common Web Pages (RCWP) computed by using following Eq. (10):

RCWP_any value from 0. , . , .5 =       .85 ∩ WP_any value from 0. , . , .5

More relative common web pages RCWP_a represent that both damping factor value indexes almost same web pages in top 25. So we can use the value of damping factor . in-place of . for certain types of web pages as discussed in above section 5.2.1. Second Parameter Web Pages got a different index w.r.t. . ( N_t ) is computed by following Eq. (11):

^any value from 0. , . , . = = ∑( WP* .85 ≠ WP_any value from 0. , . , .₅ )

Table 2. Percentage of RCWP, Ni & Number of iteration taken by PageRank method

	Relative Common Web Pages (RCWP)			Number of Web Pages Got different position ( Ni )			Number of Iteration ( la )
	CWP 0 . 7	CWP 0 . 6	CWP 0 . 5	N 0 . 7	N 0 . 6	N 0 . 5	I 0 . 85	I 0 . 7	I 0 . 6	I 0 . 5
YouTube	96%	92%	88%	64%	72%	88%	25	12	09	07
Road n/w	88%	72%	80%	84%	100%	100%	17	09	06	05
Wikitalk	96%	92%	92%	72%	84%	84%	18	10	08	06

• VIII.    Conclusion

Brin and Page have taken the value of damping factor . which is still used by many researchers. Langville et.al, state that a controls the proportion of time the random web user follows the hyperlink structure contrary to teleporting. Nowadays, there is a lot of information on Web, which is not significant to users, so that random web user does not follow hyperlink structure for long time, and they are willing to teleport to any other web page more often. Under such condition, there must be a change in value of a to get the relevant result in less time. Many researchers observed that damping factor controls the convergence speed of PageRank algorithm. We have observed in the experiment that PageRank method takes more iterations and time to converge the algorithm for

We can use this damping factor value to speed up the convergence of PageRank algorithm in many systems like web-site search engine, domain based search engines, clustering of web pages, network analysis. Where minor difference in ordering of web pages does not play an important role. In future, we will perform more experiments regarding the value of damping factor and other factors, which can speed up PageRank computation efficiently.