Дискретизация дифференциального уравнения конвекции и диффузии на основе метода контрольного объема

DOI:

Авторы статьи некоторое время занимались численным моделированием конвективного переноса. Для реализации математической модели было предложено использовать метод контрольного объема [5; 6]. Этот метод имеет ряд существенных преимуществ по сравнению с методом конечных разностей. Он гарантирует точное выполнение законов сохранения массы, количества движения, энергии на любой группе ячеек — контрольных объемов, а потому и во всей расчетной области. Для представления профилей функций между узлами сетки использовались различные шаблоны, аппроксимирующие точное решение, полученное аналитически для элементарного отрезка между соседними узлами. Применение шаблона на основе точного решения приводило к экспоненциальной схеме, требующей больших вычислительных ресурсов. Поэтому использование ее ранее считалось неэффективным. Кроме того, решения были получены для прямоугольных сеток. Дискретные аналоги и примеры расчетов на таких сетках можно найти в работах [1; 4; 7]. Использование таких же шаблонов для криволинейных систем координат приводило к большим вычислительным погрешностям, что с математической точки зрения было совершенно не оправдано. Многие прикладные задачи принципиально удобнее решать в криволинейных, например, в цилиндрических координатах. Но тогда для получения точных шаблонов нужны другие точные решения, учитывающие особенности криволинейных сеток. Современные требования к точности численных решений также изменились, и вычислительные мощности современных ЭВМ позволяют эффективно проводить сложные вычисления. Все это объясняет желание авторов получить более эффективный инструмент — расчетные схемы и алгоритмы, использующие в своей основе именно экспоненциальную схему для цилиндрической системы координат.

1.    Математическая модель конвективного теплопереноса и обобщенное дифференциальное уравнение

Математическая модель свободной или вынужденной конвекции в вязкой несжимаемой жидкости получается на основе уравнений гидродинамики, тепло- и массообмена (см., например, [2]): уравнения Навье — Стокса для несжимаемой жидкости p ^dU + (u • V)u^ = -Vp + nV2u +

1 _        .

3n V • ( V • u) + pg,

уравнения неразрывности

|p + ^V (pu)=o

и уравнения переноса тепла (аналогичный вид имеет уравнение переноса массовой концентрации химической компоненты)

/ dT       \

4 a ^{+ u} ^^т)

= Л V ² T.

В этих уравнениях скорость и (векторная величина), давление р, температура T — зависимые переменные (неизвестные функции); плотность ρ (в случае свободной конвекции зависит от неоднородности температуры), динамическая вязкость η, теплопроводность Л и удельная теплоемкость с являются физическими параметрами жидкости; g — напряженность гравитационного поля; t — время.

Дифференциальные уравнения (1)–(3) описывают процессы переноса количества движения, массы и энергии. Каждое из уравнений выражает соответствующий закон сохранения (импульса, массы, энергии). Рассматривая совместно (1–2), получаем систему уравнений для компонент вектора скорости в виде д ,    .   _ , х д-р _ „ _ х

— (рк,) + V • (puu;) — - —   + V • (/nW,) + Bi, + Vj, dt                       дх,

' i

где t , — г-я компонента вектора скорости (г — 1, 2, 3); B , — г-я составляющая объемной силы (приложенной к единице объема); V — г-я составляющая величины, учитывающей дополнительные диссипативные члены.

Из (3) и (4) следует, что t , (г — 1,2,3) и Т подчиняются обобщенному закону сохранения, которому соответствует дифференциальное уравнение для зависимой (обобщенной) переменной Ф :

д

dt(рФ) + V • (рмФ) — V • (ГVФ) + Ф, где Г — коэффициент «диффузии», а Ф — так называемый «источниковый член» (обычно представляется в линеаризованном виде, как линейная функция Ф). Здесь физический смысл Ф и Г зависит от того, какую именно величину обозначает переменная Ф. Коэффициент Г играет роль коэффициента диффузии для уравнения переноса массовой концентрации химической компоненты, коэффициента теплопроводности для уравнения тепловой конвекции, коэффициента динамической или кинематической вязкости для уравнения движения жидкости. Источниковый член Ф может включать диссипативные и объемные компоненты, которые не учитываются конвективным и диффузионным членами уравнения (5).

Для численного решения уравнения (5) будем использовать метод контрольного объема. Применение данного метода объясняется желанием получить решения, удовлетворяющие законам сохранения в расчетной области, а также сравнительно простой реализацией методики расчета и распространением ее на области сложной геометрической формы. Учитывая, что уравнения, описывающие теплоперенос, массоперенос, движение жидкости, во многом сходны, а интересующие нас зависимые переменные (компоненты) подчиняются обобщенному закону сохранения, применим метод контрольного объема к обобщенному дифференциальному уравнению вида (5).

Достаточно подробно суть метода и его приложения изложены в книге [5]. Поясним основные идеи метода. Расчетная область разбивается на множество непересекающих-ся контрольных объемов, в каждом из которых содержится только одна узловая точка. Дифференциальное уравнение интегрируется по контрольным объемам. При этом делается предположение о виде функции, описывающей изменение переменной между двумя соседними узлами. В результате получается дискретный аналог исходного дифференциального уравнения, связывающий значение переменной в узловой точке с ее значениями в соседних узлах. Метод контрольного объема гарантирует выполнение законов сохранения рассматриваемых величин как на всей расчетной области, так и на любой ее части. Таким образом, решение удовлетворяет точным интегральным балансам даже на относительно «грубой» сетке.

В [5] приведены примеры дискретных аналогов для уравнения (5), записанного в декартовых координатах. Их различие обусловлено способом выбора интерполяционных функций и профилей для вычисления значений переменных, конвективных и диффузионных потоков на гранях контрольных объемов. Для ряда задач более естественным представляется выбор цилиндрических координат (в случае осесимметричных течений, течений в трубах и др.). Тогда для построения дискретного аналога необходимо использовать другие кусочные профили, более точно описывающие изменение переменных величин между узловыми точками. Далее рассматривается вывод таких функциональных зависимостей, базирующихся на точных решениях уравнений сохранения. На основе новых функциональных зависимостей будем строить дискретный аналог обобщенного дифференциального уравнения в цилиндрической системе координат.

2.    Интегральные балансы для граней контрольного объема

Уравнение (5) с использованием уравнения неразрывности (2) можно упростить, представив в виде:

pЦ + р“ • V Ф = V • (Г V Ф) + Ф,

Запишем последнее уравнение в цилиндрических координатах (г, ср, z) (с учетом правил действий с оператором Гамильтона, [3]):

У Ф   У Ф     1 У Ф     У Ф

Р Ht ⁺ Р Уг “ ⁺ Р гдрйр + Р _д: “ ' =

+ Ф.

= 1 мг дФ\  1 _д_ /г дФ\ + 1 £ / г УФ\ г дг дг    г д р г д р г dz dz

Здесь “, “ _р , “ представляют собой соответствующие компоненты вектора скорости: “ = £ ,“ р ,“ _г) .

Преобразуем уравнение (6), умножив обе части на г :

гр   + гр“ |Ф + рмр   + гр“ |Ф = at       дг      Ур

= I ( г г |? ) + А ⁽г |^Ф ) + 8 У г |Ф ) + г Ф.

Уг \ Уг / У р \ г d р / dz \ dz /

В цилиндрических координатах уравнение неразрывности имеет вид:

Ур 1 8          1 УУ dt+ -гэ~Лри^ + ;5р(рйр) + az ^“^ =0

или

У       У          УУ дt(гp)+ эг(гр“^ + эр(р“р)+ ^гр“^ = 0.

Преобразуем уравнение конвекции и диффузии (7), используя уравнение неразрыв- ности (8):

d^t ( ^гР^Ф ) ⁺ ;| ( ^гР“ _г ^Ф ) + др ( Р“ » ^Ф ) ⁺ dz ( ^гР“ « ^Ф ) = = ^ ⁽ г г |Ф ) +    ⁽ г |^Ф ) + 1 ⁽ г г |Ф ) + г Ф.

Уг \ Уг / У р \ г d р / dz \ dz /

Уравнение (9) проинтегрируем по контрольному объему V (рис. 1) и по временному промежутку [to, to + At]. Обозначим через “ и d верхнюю и нижнюю грани контрольного объема, через w и е — левую («западную») и правую («восточную») грани, через п и s — «северную» и «южную» грани.

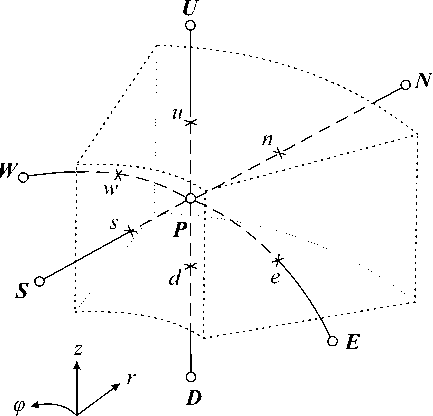
Рис. 1. Контрольный объем V с узловой точкой Р

Для удобства представления формул используем такие же обозначения в записи соответствующих этим граням значений переменных. Таким образом, через г _а обозначим значение переменной г на нижней грани, а через г _и — значение этой переменной на верхней грани. Тогда для контрольного объема V выполнено условие г _а <  г <  г _и . Аналогичным образом вводятся обозначения для значений переменных ф и г, тогда ф _е <  ф <  ф _ш , r _s <  г <  г _п . Следовательно, интегрирование по рассматриваемому контрольному объему — это интегрирование по области

V = { (г, ф, z) | r _s <  г <  г _п , ф _е <  ф <  ф _ш , г а <  г <  г _и } .

Интегрируя по области V, получаем

V to + At фш Zu  Гп

+ J x J to    фе Zd    Ta to + AtrnZu  фw

+ J x J to   rszd    фе

+

t o +At д

JTf J ^ (грФ ) dt dr dф dг +

t o

д дг (rpurФ)

^ ( ^р “ ’ ^ф )

-

-

iZ дфф )) -] дф ( Гдф )) d. ]

dг dф dt +

dг dr dt +

to+At г„фw zu j x w(£t.......-sps?))

dг dф dr dt =

t o

Т ₈ ф е

t o +At

= I IIJ г ^ dr dф dг dt.

t o        V

Размеры контрольного объема V определяются значениями Ar = r _n — r _s , Аф = = ф _е — ф _ш (рис. 2) и Az = z _u — z _d . Пусть (5r) _n — расстояние между узловыми точками Р и N , а (5r) _s — расстояние между Р и S .По такому же принципу обозначим расстояния между другими парами узлов: (5ф) _ш — между Р и W , (5ф) _е — между Р и Е , (5z) _M — между Р и U , (5z ) _d — между Р и D.

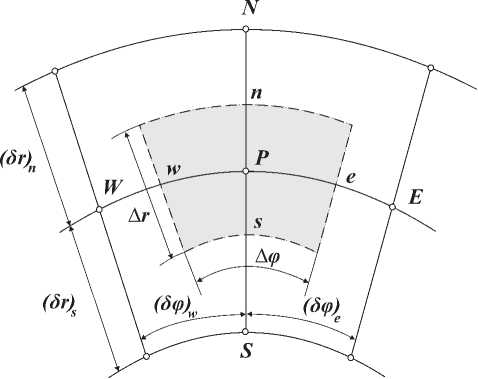
Рис. 2. Проекция контрольного объема V на плоскость ( г, ф )

Введем понятия суммарных потоков, направленных вдоль осей координат и складывающихся из конвективных и диффузионных составляющих:

J r = rpU r Ф — r Г   , J ф = ри ф Ф — ^Г , J _z = rpu _z Ф — r Г .

dr              r д ф                  dz

С учетом формул (11) уравнение (10) примет вид:

t o +At d

JTf J 5t ( ^ГРФ ) dt dr ^Ф dz +

V

t o

⁺ W [ У (^ ⁺ "дф⁺ "dz ) ^{dr d T dz} ] ^dt = W [ У ^r * ^{dr Л ф dz} ] ^dt-

Пусть J _n — значение потока J _r на грани n, а J _s — значение J _r на грани s. Также обозначим через J _w и J _e значения J _ф на гранях w и е, а через J _u и J _d — значения J _z на гранях и и d. Значения переменных Ф и р в момент времени t ₀ + At (новые значения на текущем временном шаге) в узловой точке Р будем обозначать как Ф р и Р р . Подобным образом обозначим значения переменной Ф в соседних узлах: Ф ^ в узле N , Ф р в узле S , Ф ^ и Ф _Е в точках W и Е , Ф р и Ф р в точках U и D. Значения Ф и р в узле Р в момент времени t ₀ («старые», то есть заданные значения) обозначим через Ф Р и р Р . Согласно применяемому методу считаем, что значения переменных Ф и р в узловой точке сохраняются во всем окружающем эту точку контрольном объеме. Кроме того, при интегрировании будем использовать неявную схему: в пределах всего шага по времени (t ₀ < t <  t ₀ + At) значения Ф и р принимаются равными новым значениям.

Тогда уравнение (12) аппроксимируется следующим дискретным аналогом:

( р р Ф р — Р р Ф р ) Аt + ( J _n — J s ) АфАг + (J w — J e ) АгАг + ( J u — J d ) Аг Аф — ФА V, (13)

где Ф — среднее по контрольному объему (новое, в момент времени t ₀ + Аt) значение Ф, Ау — ^—^s Аг Аф Аг. Отметим, что при г _р —    —^s выполнено АУ — г _р АгАфАг.

Аналогично интегрируем уравнение неразрывности (8):

ш

V

£ о + ^Д ^

/ at(гр) dt to

dr dф dг +

1 о + ^Д 1

⁺ W [y ( э? ^{( г р и} " ^{) +} эф ^{(р и} » ^{) +} S

dt — 0.

Введем обозначения:

F _r — гри _т , Р ф — р^, F _z — гри .

При этом F _n и F _s — значения F _T на гранях п и s, F _w и F _e — значения Р _ф на гранях w и е, F _u и F _d — значения F _z на гранях и и d.

Учитывая (15), составим дискретный аналог уравнения (14):

( ^р р ^{— р} р ) ^t ⁺ (^{F n — F} s ) ^{А ф Аг} + (^F W ^{— F} e ) ^АгАг + ^(F u ^{— F} d ) ^{АгА ф —} 0.    ⁽¹⁶⁾

Умножим (16) на Ф _р и вычтем из (13). Тогда

( ^ф р ^{— ф} Р ) p ^t--+ ( ^J n ^{— F} n ^Ф P ) ^{А ф Аг — (J} s ^{— F} s ^Ф Р ) ^{А ф Аг} +

+ (J w — F _w Ф р ) АгАг — (J e — F e Ф p ) АгАг + (J u — F u Ф p ) АгАф —

— (J _d — F _d Ф _P ) АгАф — ФАУ.

В дальнейшем задачей нашего исследования является получение достаточно хорошего приближения для значений суммарных потоков, входящих в уравнение (17). С этой целью необходимо сделать некоторые предположения о профиле функции Ф между соседними узлами с тем, чтобы рассчитать значения обобщенной переменной на гранях контрольного объема.

3.    Точные решения уравнений сохранения

Для получения лучших аппроксимаций профилей обобщенной переменной в различных направлениях найдем точные решения уравнений сохранения отдельно по каждой координате.

• I.    Рассмотрим установившееся течение вдоль оси аппликат:

  -д- ( гри _г Ф ) — дЦг Г дФК 0, аг          ог у дг /

д

— (гри^ — 0.

дг

Решаем систему уравнений (18):

дФ гр¹¹-oz

-

d ги

( г £)=o,

d / x гд!     =0.

или дФ

P^z^T oz

— I (г ^)-o, dz \ oz)

pu _z = const.

В предположении, что Ф = Ф(z), Ф'_т = Ф ф = О и Г = const, получаем краевую задачу для обыкновенного дифференциального уравнения в области 0 <  z <  L :

′′ zz

-

P^ ф ; = o, Ф(О) = Фо, Ф(L) = Ф L .

Решая задачу (19), найдем:

Ф = C i e ^{p U z z/ r} + C ₂ ,

{

^С 1 + ^C 2 = ^Ф 0 , C i e ^{p ti z L/ r} + C 2 = Ф L .

Обозначая P _z =

Р" - L

Г

(число Пекле), получим

Отсюда

или

C i

^Ф L e ^{P z}

-

Ф о

— 1 ,

С 2 = Ф о

ж   Ф-L

Ф= ePz

-

-

Ф 0

-1e

Ф -

Ф L

-

-

^Ф L e ^{P z}

-

Ф о     Ф о e ^{P z}

-

- 1

e ^{P z}

-

Ф L

_: P z z/L + f o e P z e ^{P z}

Ф 0

Ф 0

_e P z z/L

-

-

Ф £ 1^,

— 1

.

e ^{P z} — 1

• II.    Рассмотрим установившееся течение в направлении полярного угла (вдоль дуги L 0 L при г = const, рис. 3):

д-(р«фФ) — A <£ Ф дф         дф \ г дф /

д

— (риф) = 0. д ф

Считаем, что искомое решение ищется при незначительных изменениях координаты г. Поэтому полагаем г = const. Данное ограничение вполне допустимо, так как найденные нами решения будут использованы в пределах малых ячеек расчетной области.

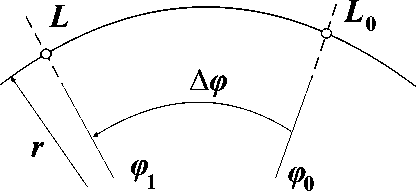
Рис. 3. Область решения одномерной задачи в направлении ϕ

Решаем систему уравнений (21):

д Ф

д

-

( Г д Ф)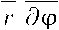

= 0,

ри _ф = const.

В предположении, что Ф = Ф(ф), Ф' _т = Ф ^ = 0 и Г = const, получаем краевую задачу для обыкновенного дифференциального уравнения в области ϕ ₀ ≤ ϕ ≤ ϕ ₁ (в пределах изменения параметра дуги I = г • ф : L 0 <  I <  L):

Ф фф - г ^Р Г ^Ф Ф ф = 0, Ф(ф о ) = Ф о , Ф(ф 1 ) = Ф 1 .               (22)

Решая задачу (22), найдем:

Ф = С 1 е^^ »/⁷ + С 2 ,

(C i e ^{rwo/ r} + С 2 = Ф о , [ С 1 е ^{г р и} ^ ^{ф 1 / Г} + С 2 = Ф 1 .

Если принять ф ₀ = 0, то система уравнений относительно С 1 и С ₂ упрощается:

( ^С 1 + ^С 2 = ^Ф о , [ С 1 е ^{г р и} ^ ^{ф 1 / Г} + С 2 = Ф 1 .

Обозначая Р _ф

= г Р^^ф-ф ₁ (число Пекле), получим

_ ^Ф 1 — ^Ф о              ^Ф 1 — ^Ф о ^Ф о ^{е Р ф} — ^Ф 1

¹ = е ^р — 1 ,    ² = 0 ^— е ^р — 1 = е ^р — 1

Отсюда

₌ ^Ф 1 ^{— Ф} 0 р _ф ф / ф 1    ^Ф 0 ^{е Р — Ф} 1

Ф еР — 1е + еР — 1 , или

Ф — Ф _о     е ^р ^ ^{ф / ф 1} — 1

Ф 1 — Ф _о      е ^р т — 1

Отметим, что решение (23) будет верным при условии г = const.

• III.    Рассмотрим установившееся течение вдоль полярной оси:

° ^p * ) - ^д ( г ^г ^) =0,                 (24)

д                                 ()

д^^Р^ т) =0.

R ₀

∆r

R

r

Рис. 4. Область решения одномерной задачи в направлении г

Решаем систему уравнений (24):

rpu„* - » ⁽гг * ⁾ =0, от дг \ ar)

rpu _r = к = const.

Рассматривая течение как одномерное, получаем уравнение относительно функции одной переменной Ф = Ф(т). В предположении Г = const задача сводится к решению краевой задачи для обыкновенного дифференциального уравнения в области R 0 <  r <  R:

кФ Г = ГФ Г + r ГФ ГГ , Ф(R o ) = Ф o , Ф(R) = Ф д , где к = rpu r .      (25)

Задача (25) приводится к виду к .        .    .                . .                             к - Г

Ф Гг = — Ф Г , Ф(R o ) = Ф о , Ф(R) = Ф д , где к 1 = —— r                                                         Г

Общим решением дифференциального уравнения является функция

• *(r) = С ГТГ + ° 2 , где к + 1 = к = ^{r p} Uk. к 1 + 1                      Г Г

„            С 1 С 1 Г , к rpu r

Пусть^{С 1} = . . ■ = дт, ^к 2 = г = —,^тогда

Ф( г ) = C i r ^- + С 2 = C i e ^{- ln r} + С 2 .

Учитывая начальные условия, запишем систему для С 1 и С ₂ :

Г C i e ^{- 2 ln д} 0 + С 2 = Ф о , | Ci e^ ln ^д + С 2 = Ф д .

Находим решение задачи (25):

Отсюда

или

̃︀

C i =

^Ф R

ек'2 in R

C 2 = Ф о

-

Ф(т) =

Ф(г) =

-

-

Ф о

_ек'2 in R o ,

^Ф R

-

Ф 0

е ^ ₂ in r

^Ф R

е ^ 2 in R

^Ф R

-

-

-

-

_е к 2 in R o

Ф 0

_е к 2 in R o

Ф 0

_е к 2 in(R/R o )

-

ек'2 in R o =

е к 2 in t

+

е к-2 in(T/R o )

Ф 0 _е к 2 In^

е ^ ₂ in R

Ф _{0 е} ^к 2 ^{in R}

е ^ 2 in R

-

+

-

-

Ф^² la ^R o

-

_е к 2 in R o

Ф _{R е} ^k 2 ^{in R} 0

_е к 2 in R o

ф 0 _е ^к 2 ^{in( R/R} o )

_е к 2 in(R/R o )

.

-

-

,

^Ф R

.

Последнее равенство можно записать в виде, аналогичном (20) и (23):

Ф

-

Ф 0

ек'2 in(r/R o )

-

Ф R

-

Ф 0

_е к 2 in(R/R o )

-

.

4.    Физический смысл точных решений

Проще всего пояснить физический смысл полученных точных решений на примере решения (20). Исследуем зависимость Ф(z) при различных значениях числа Пекле Р,.

• I.    В пределе при Р , ^ 0 (в случае «чистой» диффузии) получаем

  lim

  
  

  (^P z ,/L

  
  

  _-

  
  
  
  

  P z - 0

  
  

  е^Pz

  
  

  _-

  
  
  
  

  = lim

  
  

  P z - 0

  
  

  Р , z/L

  
  

  z

  
  

  Р ,

  
  

  L

  
  

  или Ф = Ф ₀ + (Ф _L

  
  

  _-

  
  

  Ф о ) z,

  
  

  то

  
  

есть Ф(z) линейно зависит от z.

• II.    При Р , » 1 для значений z, отличных от нуля, имеем

  и

  
  

  еР-z ,/l

  
  

  е^Pz

  
  

  Ф = е

  
  
  
  

  _-

  
  
  
  

  _-

  
  

  P z

  
  
  
  

  ₍ P z (, - L)/L = _е

  
  
  
  

  P z (L - ,)/L

  
  

  ^{( L - , ) /L} ф _L + ^1

  
  

  _-

  
  

  е

  
  
  
  

  P z

  
  

  (L - ,)/L^

  
  

  Ф о ,

  
  

  то

  
  

есть, чем больше Р , , тем больше влияние Ф ₀ на грани контрольного объема.

и

то

III.

есть,

IV.

вид:

При Р , <

-

1 получаем

(.P z ,/L

еPz

-

е

| P z V/L

-

-

е

| P z |

-

-

е

| P z | ,/L

Ф= 1

-

е

| P z | ,/l)

Ф L + е

^{| P} z ^{| ,/L}$_n 0 ,

при отрицательных значениях Р , чем больше | Р , | , тем больше влияние Ф _L .

Производная Ф , (если рассматривать Ф как функцию одной переменной) имеет

аФ

az

a

=    Ф0 + az

gP z ,/L

еPz

-

-

^(ф L ^{— Ф}о)^ =

Ф L

-

Ф 0

еPz

-

_еР-. ,/L ^ ^Р ^

L

.

На грани контрольного объема, расположенной посередине между узлами (то есть при г = L/2), имеем

Ф ; (L/2) =

^Ф л ^Ф 0 p_z /2 ^Р е ^р — 1 ^С L

^Ф Д ^{— Ф} 0      ^Р г

L    е ^р / ² — е - ^р / ² '

Таким образом, при больших значениях | Р _; | производная Ф ( (L/2) близка к нулю (диффузия почти отсутствует).

Физический смысл точного решения (23) легко пояснить, исследуя аналогичным образом зависимость Ф(ф) при различных значениях числа Пекле Рф. При этом и результаты получаются точно такие же. Немногим отличается исследование зависимости Ф(г) в (26). В частности, при к2 ^ 0, что равносильно условию Рг ^ 0, получаем е^2 infp/^o) — 1 in т — 1П д0 fc™ ек2Ид/д0) — 1 = lnP — InPo'

В этом случае зависимость Ф(^) нелинейная. Однако, как и для Ф(г), при к ₂ ^ 1 выполняется

^ 2 1п(г/Д о )

________________ М1п(рД о ) - 1п(Д/Д о )) _ p-^fc 2 1п(Д/г)

_е ^ 2 1п(Д/Д о ) _— 1 ~ ^{е                        е}

и

Ф(г) = Ф 0 + (Ф д — Ф 0 )е ^- ^ ^{2 1п( д/г )} .

Таким образом, на грани контрольного объема более существенно влияние Ф ₀ .

При к ₂ ^ — 1 имеем

Ф _— Ф 0     _е ^2 ИР-Ro) _— 1

ф д _— Ф 0     е ^ 2 ^{1п( д/д} о ) _— 1

и это означает, что на грани контрольного объема значение Ф(^) близко к Ф д .

5.    Экспоненциальная схема

Используя полученные аналитические решения (20), (23) и (26), построим дискретный аналог для обобщенного дифференциального уравнения.

• I.    Найдем приближение для значения потока J _; на верхней грани и контрольного объема.

В качестве профиля между узлами Р и U используем точное решение (20), заменив Ф ₀ на Ф _р , Ф д на Ф и , а L на расстояние (5г) „ между точками Р и U . Тогда

Ф = Ф_Р + ^Ф и — ^{Ф р} |7 '" ' ' ⁵ '   — 1 ) , Р_и = ( E^LSfL,  0 <  г <  ( 5г ) .

е — 1                         “

Обозначим: D; = —, m; = —. На верхней грани контрольного объема имеем F» = 5гг

= ( гри _г ) , D » = -—»—, т » = -——. Здесь г » — расстояние до грани и от узла Р .

»          (5г)»

Поток J » можно представить в виде

J » = F »

Ф р + ^Ф и ^{Ф р} ( е ^р “ ^/т “ — 1 ) е ^р“ — 1 V           /

—

Г Г »

Ф и — Ф р Р » е ^р “ — 1 ( 5г ) »

е^и /тц.

Г1 П A    О     (PUZ)u /  \      Fu где ru — D u (5г) , Рц     —   (5г) и —  TF'

^u         r u ^/u    rD _u

Следовательно,

J u —F u

[ фр +

^Ф и - ^Ф Р

е ^{Р и} — 1

( е Р и /^т «

-

-

F u

Ф и

-

е ^{Р и}

^ф Р

-

_е Р_и/т _и

— F u

[ Фр +

^ф р - ^ф и

е ^{Р и} — 1

•

Таким образом, J _u не зависит от расположения границы раздела между узлами Р и U (m _u в выражение для потока J _u не входит).

Аналогично на нижней грани d контрольного объема выполняется равенство

J d — F _d

Ф р +

^ф р - ^ф Р

е ^р

-

( 5г

d

II. Найдем приближениe для потока J _ф на «западной» грани w контрольного объема.

В качестве профиля между узлами Р и W используем «средневзвешенное» по этой грани значение Ф на основе решения (23), заменив Ф о на Ф _Р , Ф 1 на Ф ^ , а ф 1 на (5^) _w (см. рис. 2). Тогда

( ри где Fd — (rpuz)d, Pd — —

)_d, (5г) _d — расстояние между узлами Р и D.

Ф — ФР + 5^—^ (V р ■ф (5ф ■ — 1) ,  Р— — r P^(5ф)— ,  0 < ф < е ^   1                                         —

Обозначим: D _ф — ——, т _ф

,     .                   Г—

^— (^риф) , ^D — ^— С ^ ,

^{—            r 5}Ф'

Поток J_— можно представить

δϕ —     .

ϕ т— — в виде

На «западной» грани контрольного объема F _w — ( 5ф )

----— . Здесь ф _ш — угол до грани w от узла Р . ^ф ш

J — — F — [Фр + ^Ф ^ ^{Ф р} ( е ^Р ™ /^ ™ - 1 ) е ^{Р ш} — 1 \           /

Г — ^Ф ^ - ^ф р ^Р — _ер_ш / _тш r е ^{Р ш} — 1 ( 5ф ) _—

где ^Г — ^{— rD} — ( ⁵ ф ) _— , ^Р — ^{— r} Р^ф)^— ( ⁵ ф ) _— ^—    .

^Г —           ^D —

Следовательно,

J = F [^ф_Р + —__^Фр (е^р'/^т'^г™ - 1)1

° —    — р ⁺ е Р ^    1 v

—

^Ф ^ ^{— Ф} Р _е Р _ш /т _{ш —} е ^{Р ш} — 1

= F

—

Ф р +

Ф р — Ф ^

е ^р ™ — 1

Таким образом, J _— также не зависит от расположения границы раздела между соседними узлами.

На «восточной» грани е контрольного объема выполняется:

J e —F _e

Ф е +

^Ф Е ^{— Ф} Р

е ^р е

—

( рМ ф )

где E _e = (рМ ф)_e , Р _е = t —-—- (5ф) _е , (5ф) _е — угол между узлами Р и Е . ^г -

• III.    Найдем приближения для потока J _T на «северной» грани п контрольного объема.

В качестве профиля между узлами Р и N используем точное решение (26), заменив ф0 на фР, фр на ФN, R0 на Rp, R на Rn, а Ат на (8т)п = Rn — Rp (см. рис. 2). При этом Rp < т < Rn = Rp + (бт)п. Тогда фN -Ф = Фр + —тр-еРп

-

ф р

— 1

_е (Р п /£)1и(г/Р р ) - 1) ,

где L = In ^{R n} , Р п = Т п Р_р^^п ln ( 1 + ( S t ) /R p ) = ^R P             ^Г п     ^V

Т п

( ^р^ г)п

"TT'L-

Обозначим: D _r

г

ln(1 + S t/R p ), ^т

ln(1 + S t/R p )

—-—;—----—, St — расстояние меж- ln(T/RP)

ду соседними узлами

вдоль полярной оси. На «северной» грани контрольного объема

величины E r , D _r и т _т принимают значения Е^ = т _п ( ри _т ) _п , D _п = -^, т _п = ——^ .

Здесь т _п — значение полярного радиуса, соответствующее грани п.

Поток J _п можно представить в виде

^J п = ^Е п [^фР +

^ФN ' е ^{Р п}

-

^ф р

— 1

(_ePn^m„ _ AT _ _r Р ^ФN " у ^е                  ' п п е Р п

-

ф р Р п 1

^{— 1 L Т} п

, Рп /т п

где Г п = D n L, Р п = Т п

P^^lU_l = Fe

Г п       D п

Следовательно,

J п = F п [фр

. ^ф v е ^{Р п}

-

^ф р

— 1

( еР п /т п

— 1   —

5nj ^п е ^р п

-

^Фр> ^п/т

— 1

= F п [фр

+

^ф р

-

^Ф N

е ^{Р п} — 1

] •

Как и в предыдущих случаях, Jn не зависит от расположения границы раздела между

соседними узлами (т _п в выражение для потока J _n не входит).

Аналогично на «южной» грани s контрольного объема выполняется:

^J s = ^E s [^ф 5 +

^ф5 • _е ^р =

-

^ф р

— 1

] •

(рит где Es = ts(pur)s, Рs = ts—-—s In ^1 + (5т)JRsj, (St)s — расстояние между узлами Р и S.                        S

Подставим выражения (27)–(32) для суммарных потоков на гранях контрольного объема в уравнение (17).

—	( Ф р - Ф 0 р ) Р р ^^ + ( f „ [ ф р + ^^^ ] -F n Ф р ) AyAz - At                 е р- — 1 ( f s ^s + ф р - “Т j — F s Ф р ) AyAz + ( F w [ ф р + ф р - -^ j — F w Ф р ) ArAz -
-	( F e [ ф е + Ф ’ р   Ф р j - F e Ф р ) ArAz + ( f u [ ф р + ^tt~_ Ф1 Р j - F u Ф р ) ArAy - ( F d [ ф о + ФР    ' ] - F d Ф р ) ArAy = ФЛК

Среднее значение источникового члена Ψ представим в линеаризованном виде: Ψ = = Ф р + Ф р Ф р , где коэффициенты Ф с и Ф р определяются видом дифференциального уравнения.

Приводя подобные члены, имеем:

(Р 0 AV    F „   д д      е р =              F w (  At   1 е р - - 1 A^Az ' е р - - 1 F Л ф Л** 1 е р - - 1 ArAz + вРе „ . .        Fu    .            ePd „ .                  \ +     F e ArAz +      ArAy +      F d ArAy  Ф р AV Ф р е р е - 1             е р “ - 1            е Г а - 1                     / ф р         A^Az ф ^        F s A^Az ф s         ArAz ф ^ At         е р - - 1              е р - - 1                 е р - - 1 ер „ . .               Fu,     . .               ер<1 „ . .             , F e ArAz Ф Е        ArAy Ф и        _Fd Ar Ay Ф п = Ф с AV. е р е - 1                е р “ - 1               е р < - 1 Получаем следующий вид дискретного аналога: а р Ф р = а ^ Ф ^ + a s Ф 5 + а ^ Ф ^ + с е Ф е + а р Ф р + а д Ф о + Ь,       (33)

где

а р = а р + a E + a s + a w + а Е + а р + а о - Ф р AV, F n    А д              ер-       А А               F w    А А а ^ = ерг - 1 AyAz,  a s = е ^ - 1 F s Ay Az,  a w = ерт - 1 ArAz, ер<:   „ .                   F u                          ер <   „ . а Е = Р 1 F e ArAz,  а р =       ArAy,  а д = р     Fd Ar Ay, е р е - 1                     е р “ - 1                   ер< 1 - 1 а р = PaA V,   Ь = а 0р Ф 0р + Ф с AV.

Значения чисел Пекле P_Tl, P _s , P _w , Р _е , P u , P d , «расходы» F_n, F_s, F w , F _e , F _u , F _d и «проводимости» D _n , D _s , D _w , D _e , D _u , D _d вычисляются по формулам, полученным в ходе построения дискретного аналога. Приведенную схему, использующую точные (экспоненциальные) решения, называют экспоненциальной.

6.    Общая форма дискретного аналога

Для дискретного аналога (33) можно получить более общую формулировку, если воспользоваться исследованием С. Патанкара [5, c. 78]. Представим, например, суммарный поток Jn как среднее взвешенное значений обобщенной переменной в соседних узлах:

или

где

Jn — [Fn +--p---7 ] ФР--p---7 ФN eP — 1J      eP—

^J * ^— у ^— В ^ф р - А ^ф N , ^D n

А —, eP — 1

__ F

^{В — F}n + P 7 ^{— А} + ^F n . e ^P " — 1

При изменении направления координатной оси на противоположное меняется знак F _n , а коэффициенты А и В меняются местами. Тогда

• — J * — В * Ф N — А * Ф р , А * = А( — F „ ) — В(^), В * = В (—F^ — А(^).

Таким образом, при противоположных направлениях координатной оси, то есть при значениях F _n разных знаков, выражения для коэффициентов А и В различаются. Решения (34) получены при условии, что направление вектора скорости и совпадает с направлением полярной оси (при F _n >  0). Если и и полярная ось противоположно направлены, то F _n <  0. Тогда

А(F_n) — А( —| F „ | ) — B( | F n | ) — А( F | ) + | F „ | — А( |^| ) — F „ .

Соответственно, при F _n >  0 выполнено равенство А(F _n ) — А( | ^ | ).

Введем оператор

А(F)— А( | F | ) + max ( — F ;0 ) ,                        (35)

|F | где А(|F|) —    ----. При этом e|P | — 1

В(F ) — А( | F | ) + max(F; 0).

Коэффициент ctN запишем, используя (35):

Fn cn — -б----ЛфЛг — Dn А(F„) ЛфЛг — \Dn А(|F„|) + max(—Fn; 0) ДуДг.

eP" — 1                                    LJ

Аналогично получаем выражение для а д , используя (36):

ePs                                                         г"1

а д — -б---7F_s ЛуЛг — D _s В(F _s )ЛуЛz — D _s А( | F _S | ) + max(F _s ; 0) ЛуЛг.

eP= — 1                                         LJ

Применение операторов А(F) и В(F ) позволяет получить обобщенную форму записи и для других коэффициентов. Тогда окончательно дискретный аналог принимает вид:

Cp фр — Cn ФN + адФд + Cw Ф^ + Се Фе + Си Фи + Cd Фр + Ь,(37)

где

ap = ap + cn + ctg + aw + ap + ay + ay — Фр AV, cn = Dn A(Pn)A^Az,  as = Ds В(PV)A^Az,  aw = Dw A(PW)ArAz, aE = De В(Pe)ArAz,  ay = Du A(Pu) ru ArA^,  aD = Dd B(Pd) rd ArA^,

-•- ^pyr

b = a ? Ф ? + Ф _с AV,

а операторы A(P) и В(P ) задаются формулами (35, 36).

Полученный дискретный аналог (37) обобщенного дифференциального уравнения (5), записанного в цилиндрической системе координат (9), может быть использован для численного моделирования конвективного тепломассопереноса в условиях ламинарных и турбулентных течений вязкой несжимаемой жидкости в замкнутом объеме. Вопросы реализации данной модели, касающиеся расчета поля скоростей, использования граничных условий различного рода, остались за рамками данной статьи, поскольку здесь решалась задача получения экспоненциальной схемы применительно к цилиндрическим координатам. Учет особенностей реализации модели необходим для корректной аппроксимации функции Ф между узловыми точками, для определения вида операторов A(P ) и В(P ) и формул расчета чисел Пекле для переменных r, ф и z . Использование дискретных аналогов, построенных на основе точных решений уравнений переноса, может оказаться более предпочтительным с учетом современного уровня вычислительной техники.