Дискретизация двумерной области

Подстановка задачи: Пусть ограниченная область. В области G = ^t,x,y^\t e (0,Г), (x, y) e Qj найти вектор-функцию и , удовлетворяющую системе

Lu = F(x, у, f)

с граничными

Du^g^y)

и начальным i/(O,x,y) = i/o(x,y), (x;v)eQ                                         (3)

условиями. Здесь aQ - граница области Q, '. -дифференциальный оператор, -прямоугольная матрица, 1ф,у)~заданная вектор-функция, и^,х,у) = (и},и2,...,имУ - неизвестная, а F(t,x,y}^[f{, ff^1 - заданная вектор-функция.

Будем считать, что смешанная задача (1)-(3) поставлена корректно. Для численного решения задачи (1)-(3) прежде всего предстоит дискретизация области .

Аппроксимация области.

Двумерная ограниченная область аппроксимируем следующим образом. При описании границы области в качестве составляющих ее частей могут использоваться отрезки прямых и дуги окружностей. Началом некоторой части границы s считается та ее концевая точка, при движении из которой по s область остается слева. Отрезки прямых определяются двумя точками – концами, а для дуг окружностей дополнительно задается точка центра окружности. Например пусть дана область Q (рис.1). Границу области

Граница ao аппроксимируется следующим образом:

1. По виду an выберяем точки.

т i «л; л)^: ^2 (^x2; у 2 )'-"Tn <^x„; y„)

Здесь FJF-yr,, - выбранные точки, ( У’У, ) ( i=1,…,n ) - их соответсвующие координаты, : - символ отделяющий точек.

Эти точки могуть быть началными или конечными точками отрезков или дугов, либо центрами дугов.

• 2.    Часть границы расположенный между двумя точками по виду

• 3.    Часть границы расположенный между двумя точками по виду

заменяется отрезком:

.

Здесь ^Mi e {^1^2,- - ,Tn] ( i=1,…,k ) точки, L,(TM,;TMM) ( j=1,…,s ) ^Mi (   - начало j-го отрезка), ^Mi+1 ( ^Mi+1 - конец j-го отрезка), LJ - j-й отрезок.

заменяется дугой:

.

Здесь ^Mi ^e {^1’^2’" ' ’^n} ( i=1,…,k ) точки, ^ / C^Mi ’ ^Л«+1 ’ ^Mi + 2 ) ( j=1,…,m )

( i=1,…,k -2) ^Mi ( ^Mi - начало j-й дуги) ва ^Mi+X ( ^Mi+1 - конец j-й дуги) , ^Mi+2 - центр ^Di дуги.

После аппроксимации границы dQ области Q . Область Q заключи м в наименьший прямоугольник со сторонами, паралельны ми осям Ojc и :

. Проведем прямые                                  , y = yj=c + hyj       {j = ^...,Ny,hy=—~) пересекающие отрезки, соответсвенно, [a;b], c, cl ] . В результате область Q покроется равномерной сеткой (рис.1)

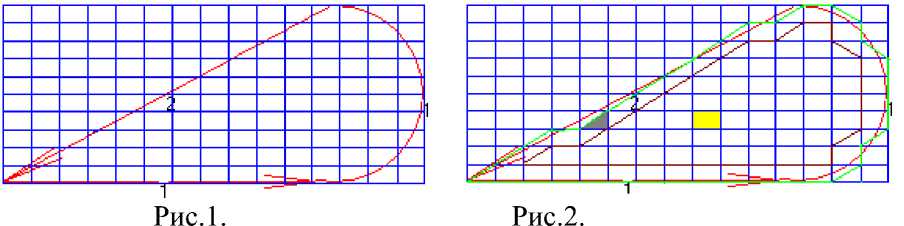
Точку пересечения прямых    x = xj = a + hj и У = Уj=c + hj, называемую узлом сетки, обозначим через             .

h

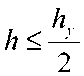
1-определение. Узел, находящийся на расстояние ^ ~^ или от dQ , или лежающий на dQ называется граничным узлом.

На рисунке 2 граничные узлы соединены линией зеленого цвета.

2-определение. Узел, лежащий внутри области Q и являющийся соседным узлом граничного узла, называется околограничным узлом.

На рисунке 2 околограничные узлы соединены линией коричневого цвета.

3-определение. Узел, лежащий внутри области Q и не являющийся соседным узлом граничного узла, называется внутренным узлом.

4-определение. Узел, не лежащий внутри области Q и не являющийся граничным узлом, называется внешным узлом.

Сетка разбивает область ^л на части (элементы). Каждый элемент является прямоугольником (на рис.2. желтого цвета) или треугольником (на рис.2. серого цвета). Элемент обозначим через К . Элементы, одной из вершин которых является узел Му , называются элементами этого узла Объединение этих узлов обозначим через . Тогда справедливо равенство

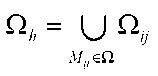
С помощью каждого типа и порядкого номера узла отдельно храняться все данные смешанной задачи (1)-(3) относящейся к этому узлу в базе данных.

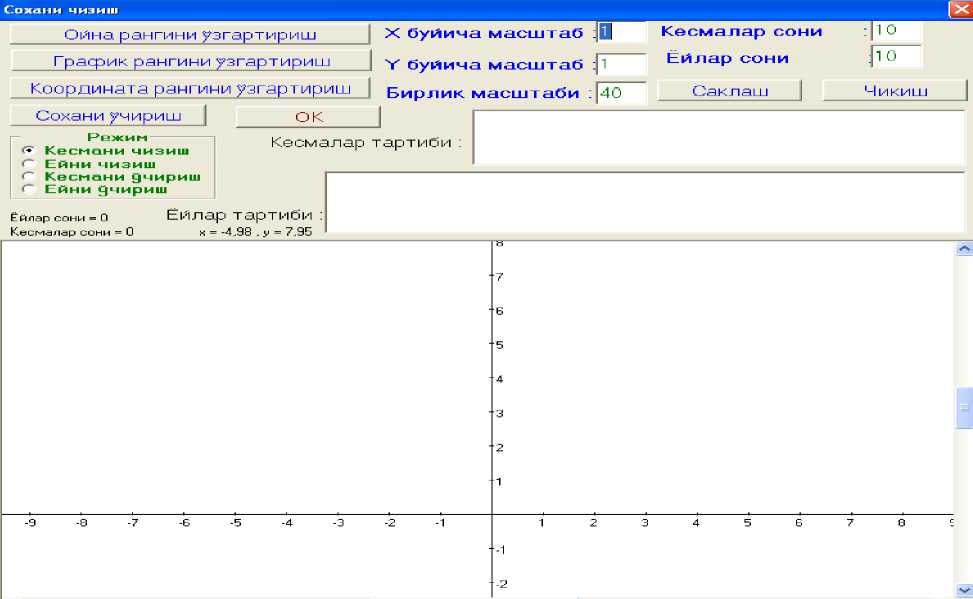
На основе этого алгоритма создана программа “Соҳани чизиш” .

Ниже с помощью программы приведены некоторые аппроксимации областей.

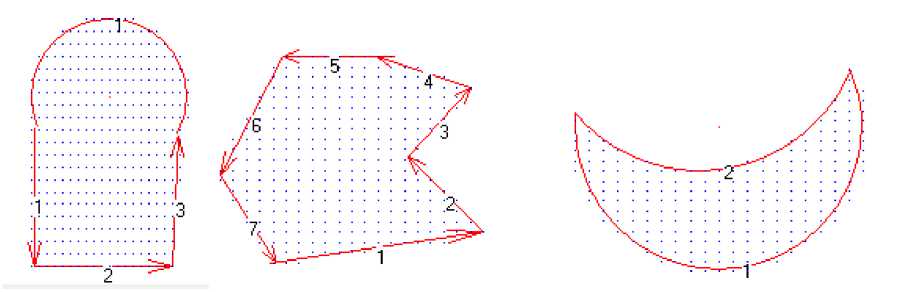
Бу расмларда соҳа чегараси ёйлар ва кесмалар билан аппроксимация қилинган, тўр тугунлари нуқталар кўринишида тасвирланган.Ёйлар ва кесмалар алоҳида номерланган. Кесмалар йўналишга эга.Кесма йуналиши кесманинг бошланғич нуқтасидан охирги нуқтаси томон йўналган.

Программа “Соҳани чизиш” имеет вид:

Адабиётлар:

• 1.    Годунов С.К. Уравнения математической физики. М.:Наука,1979,372с.

• 2.    И.А Сандер., Программа дискретизации двумерных областей общего вида

  Препринт 860. Вычислительный центр СО АН СССР. Новосибирск 1989

• 3.    Марчук Р.И., Агошков В.И. Введение в проекционно-сеточные методы.-М.:Наука,1981.

ФОРУМ МОЛОДЫХ УЧЕНЫХ №6(106) 2025