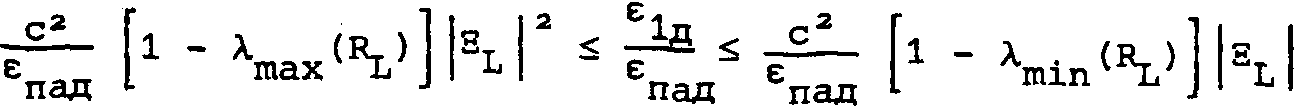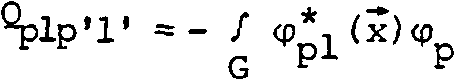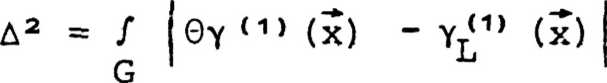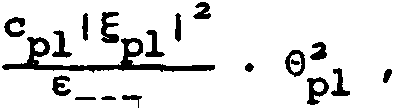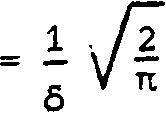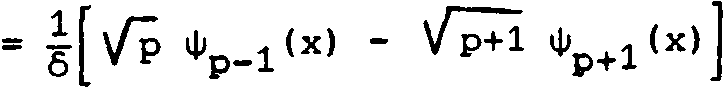Дискретизация в эталонных модовых элементах компьютерной оптики

ДИСКРЕТИЗАЦИЯ В ЭТАЛОННЫХ МОДОВЫХ ЭЛЕМЕНТАХ КОМПЬЮТЕРНОЙ ОПТИКИ

Свойства модовых оптических элементов компьютерной оптики [1-3] в определенной степени определяются операцией дискретизации их функции пропускания или отражения. Первые оценки погрешностей дискретизации в задаче анализа поперечномодового состава когерентного излучения получены в работах [1, 2] .

В данной работе изучается структура световых пучков, восстановленных с дискретизированных модовых оптических элементов, выполнены оценки энергетической эффективности и точности формирования поперечно-модового состава при наличии дискретизации.

• 1,    Преобразование светового пучка при наличии дискретизации функции пропускания

Эталонный световой пучок с комплексной амплитудой

Е(х)

(p,D ei_T

Vpl^)'

х е g,

(i)

ЕР1 = Vv exP(ibPi> селективно содержащий L > 1 поперечных мод ф^^(х)с номерами (р, 1) G IL мощностями ц ч и фазами Ь п может быть получен из освещающего пучка Е(х) с помощью plpl комплексного пространственного фильтра с функцией пропускания w (х) =        ,(3)

Е(х) где I - множество, содержащее L двойных индексов (р, 1 ); х = (х,у) - декартовы координаты в плоскости сечения G пучка. В компьютерной оптике рассматривают функцию комплексного пропускания

Г(Х) = f(^2- , V) ,                                                          (4)

max

W v = max lW(x)l,                                                         (5)

x GG удовлетворяющую условию |Г(х)| < 1 и получающуюся путем кодирования способом f функции (3). Способ кодирования подбирается таким образом, чтобы в первом дифракционном порядке, идущем под наклоном, соответствующем пространственной частоте v, восстанавливалось поле у(1), пропорциональное Е(х)

Y(1)(x) = сЕ(х)exp(i2nvx), c=const.                                        <6)

Для этого компонента г(1) функция пропускания Г(х), соответствующая первому по рядку, должна удовлетворять соотношению

Г'^Сх) = a ^L exp (i2nvx), max где

a

cWmax

При v = 0 первый дифракционный порядок переходит в нулевой. Заметим, что коэффициент а определяется только способом кодирования f.

Например, для амплитудных и фазовых модовых оптических элементов с несущей можно показать, что имеют место те же формулы, что и для амплитудных и фазовых дифракционных решеток соответственно а _ а ДА а =  —

Ф

_ _ т /тах о\ а = 1^    — р) , где ДА € [0,1] и ^тдх^Е0^] ~ диапазоны амплитудного пропускания и фазового

(Ю)

сдвига соответственно регистрирующей

среды; £ £ [0,1] - глубина модуляции; обычно

Ф = n.

max

В технологии компьютерной оптики мощью дискретного фотошаблона. Будем

функцию пропускания Г(х) реализуют с посчитать, что фотошаблон вычерчивается на

фотопостроителе с дискретным позиционированием и строчной разверткой, обеспе-

чивающим Nn х Na pa 6 х 5 каждая.

отсчетов с равномерно засвечиваемыми ячейками разрешения разме-Область G представляет таким образом прямоугольник d1 х d3,

где di = N16; da

= Na6

Соответствующая дискретизированная функция пропускания имеет кусочно-постоянный характер и описывается соотношением [4]

~        Ni

Г(х) = 2

п=1

N2

m=l

Г(х )х__(х) пт пт

где х = (х пт п

у ) - центр ячейки разрешения

G номер (n, т) пт

хпш(х)

1, X€Gnm пт

0, х 6 G пт

Из (7), (11) соответственно получаем где

Р<” (х) = а

^Х ' exp i2nv x ) max

W(x)

Ni

2 П=1

Na

Wtx^x^txlexp^nvtx -m— i

X ) 1

nm J

В силу соотношений (7), (13) функция W(x) аппроксимирует функцию комплексного пропускания W(x) (3) .

Формируемое модовым оптическим элементом компьютерной оптики поле в первом порядке может быть представлено в виде

Y(1)(x) =E(x)f(x) = cn(x)exp(12nvx)

Функция

П(х) = Е Е ,<с , (х) (_Р,1) ет р¹ р¹

Li согласно (1) , (14) представляется в виде n(x)-= Е EDi

и отличается от эталонного пучка g(x) заменой ортонормированных модовых функций ^bi^)' (Р'1) € ^ на ‘’возмущение” модовые функции

Ni Na

^1

run

1 x

E (x )

nm

Ф !(x) = E(x) E E pl          n=l m=l

Xnm(x)exp[-12nv(x - xnm)]; (p,l) eiL.

• 2,    Возмущения модовых функций при дискретизации

Будем интерпретировать [5] функции Qp^fx) (р,1) € 1^ как результат воздейст вин возмущений hpl(x) = Фр1(х) - Фр1(х),  р,1 €IL                                      (19)

на ортонормироваиные модовые функции Фр^(х), (p,l)CIL. Возмущения обусловлены дискретизацией и зависят от способа кодирования модовых элементов компьютерной оптики. Для исследования структуры модового пучка при наличии дискретизации введем матричные элементы

Н . л, = / h* (х)ф М1(х)а*х(20)

pl p’l’ G pl р'Г (* - символ комплексного сопряжения).

Возмущенные модовые функции представляются через ортонормированные по формуле фр1(х) = Фр1(х) +р,д, Нр1 р'1* фр<1'(х)'

где суммирование производится по всем р’ = 0,1,2...; I1 = 0,1,2... . Соответственно поле и(х) (17) может быть представлено в виде

П (х) = Е и. ^pl^^'^

р,1 р р где

И

Нужные для компоненту

Ер1

Е

Е (р’,11) €1

Нр'1'р1 ^р'1' при (Р'1) G IL

(р',1') еI HP'i'pi ^p'l'

при(р,1) € 1^.

построения эталона Е (х) (1) моды ф^^

(р,1) €1Т составляют лишь

Пт (х) = Р п(х) = Е И -i Ф.

L L         (p,i ) 6i pl поля n(х) (PL - оператор проектор на базисные функции ф ,, (р,1) €IL> . Для удобства дальнейших выкладок удобно ввести L-мерные векторы

Е- • (Е , : (p,D 61 ); Н = (п_п1 : (р,1) 61 ), Li                                                   Li           Ju                                                   •*-*

а также матрицы L x L el = [^ppi * ^ii1 2 (P*D e ^Z (P*^ ^ gil^ *

HL = ^plp’l’ 2 (p,D €Ii/ (p '^ ^ GIL^f

Фт = ET + HT ,

где брр, - символ Кронекера.

В векторных обозначениях формула (23) дает нт = Ф*гт = (Ет + Н*)г ,                                                        (26)

L L L Ь Ь ь где * - символ Эрмитова сопряжения матрицы. Ниже будем употреблять обозначения (• , •) и |-| для евклидова скалярного произведения и нормы векторов.

• 3,    Энергетическая эффективность при наличии дискретизации

При освещении модового оптического элемента пучком со световым потоком е = / |E(x)!2d2 х(27)

пад G в первом дифракционном порядке формируется пучок у(1) (х), содержащий как тре буемые моды

идущий на формиро

ут(1> (х) = PTY (1) (х) = СПТ (x)exp(i2nv х), LLi так и "паразитные" моды других порядков. Световой поток е^д, вание требуемых мод ф ^, (рД) 6 1^ определяется по формуле е = j |vtn (х)|2d2x = с2/ !пт (х)I 2d2x =

1Д G LG

= С2^, ^) = c2(El - Rl)8l, 8l), где

-Ч = фьф£ - EL = »L + HL+ «Х-

Б1д

Энергетическую эффективность т--- модовых оптических элементов будем оценивать пяд по отношению к световому потоку освещающего пучка (29)

• -15-    = -2L. ( (Е- - R- (8 ,8 )                                                    (31

6           Е             L Li Li Li *

пад пад

В случае L=l, когда эталон £ содержит лишь одну поперечную моду Е пФ ] (х) , со отношение (31) принимает вид е1д епад

Е пад

11 + нр1р1|2'

где индексом ’р!’ помечаются ранее введенные величины, относящиеся к одномодо вому пучку. Наоборот, в случае, когда рассматривается класс всевозможных этало- нов g (1) , содержащих ровно L мод, можно пользуясь теорией квадратичных форм

[б] получить оценку

где Х~. (R,) hX^^JR-) - минимальное и mln L шах 1/ пряженной матрицы R^. Заметим, что при дут достигаться.

максимальное собственные числа самосо-

варьировании

S границы оценки (33) бу-

В отсутствие дискретизации Н

О

формула (32) принимает вид

Е         Е пад пад

I 12

|Ер1| '

а неравенство (33) превращается в равенство

Е        £ пад пад

Таким образом, при наличии дискретизации модовых оптических элементов энергети- ческая эффективность снижается в [1 - А . (Р )]"1 т Г1 - А (Rj]-1 раз за

[ min Ъ J [      maxv ъJ       ■ счет дифракционного рассеяния светового потока в высшие дифракционные порядки, в том числе в (1 + 2ReHpipi

plpl

раз при

Через моды высших порядков, входящих в пучок у1

= / |y⁽¹⁾ (х) - Y_T⁽ⁿ (х) l²d²x = / Iy ^<1) (

1высш I               L I          „ I

уходит световой поток

d х - Е

В силу формул (15), (17), (29) получаем е *          ™ с* Г

1ВЫСШ       J

G

П(х) |²d²x - е_1д = сЧС^ _ Q_l)S_lS_l),

где

°L = Qplp'l- ! (Р'П eiL ? (P'l’l€IL]

1*(x)d2x * 5рр'6Ц' •

• 4,    Влияние дискретизации на поперечно-модовый состав

Дискретный модовый оптический элемент, синтезируемый методами компьютерной оптики, несколько изменяет распределение мощности между формируемыми модами

^pl^' (P'l) ^г/ а также Фазы М°Д в пучке Y^1> (х) по сравнению с требуемым пучком у(1) (х) (6). В силу снижения энергетической эффективности при дискрети зации, сравнению по модовому составу подлежит пучок ут(1) (х) с пучком 0у<1) (х) , где 0 < 0 < 1.

Представим виртуальный интерферометр, выведенный на нулевую полосу, в плечи которого подаются пучки 0у<1} (х) и -ут(1) (х) . Тогда интенсивность в интерферо- грамме будет описываться формулой

) ©У < 1 > (х)  - у<1) (£) |2,

■U а световой поток разностной интерферограммы

может рассматриваться как критерий точности формирования модового состава.

Используя (6), (24) и ортонормированность модовых функций нетрудно преобразовать формулу (38) к виду

Д² = с² |0S_T- ь I ².                                                                  (39)

L Li

Критерий Д2 (39) принимает минимальное значение

Д²= c²[(#_l, #_l) - 0²(S_l, E_l)] = c²([(l - ^^гЛ^ь' У              ⁽⁴⁰⁾

при оптимальном значении

Н +Н.

Re(S , Н ) 9 = _ ^ь--

L

L

Оценивая значения квадратичных форм (40)

(41) с самосопряженными матрицами

получаем следующие оценки д2 и 0:

с2[1 _ 02 _ A(R)]lSI2 < Д2 < с2[1 - 02 - A (^)J ISLI =

max

Нт+Н*                    Н +Н*

^La - ) < 0 < 1 + А . (—М¹) 2                  min 2

Относительная погрешность формирования поперечно-модового состава при наличии

дискретизации равна д2              ((El-Rl)Sl,=l)

о = ----------------- = --------------—

/I©у <¹> (х) |²d² х 0²(E_l,E_l)

Другим критерием точности является среднеквадратичная ошибка формирования

модового пучка

Д2 = / |у «D (X) - у<1> (х) I2d2 X

Ф G

• с соответствующей относительной погрешностью

.a           J 1Е(х) - п(х)l³d³ X

• 6 ² = --------£_____________________

  
  
  
  

ф У ly m (х)l2d=(x)     / IE(x)l3d3x

G                     G

Из формул (17), (1) , (37), (19) можно получить оценку

_           (Q-B-,8.)

W«L>⁵ ^ * -^ „ ; * ^Х_ЮА' -^k“L'°L⁾

где

QT - - (QT + Н_ + Н?) .(48)

Li             Li Ъ JU

Для случая формирования эталона одной моды ф^^ (L=l) оценки принимают вид ер1 -1 * ““plpl-“”

^1 - ^j1 - е3 » 2 р=вр1р1 ♦ lHplpll3]IEpll3 .

• - ICplEpll=(T»Hplpl)-,<50>

  б

  
  

  ^(1+ReHplpl)³

  
  
  
  

  ⁶^Р1 Заметим,

  
  

= -(Qplpl + 2ReHplpl).

что при вещественных значениях Н ^р^ имеет место равенство е1д е пад

пад

показывающее, что множитель О2 характеризует непосредственно уменьшение энергетической эффективности из-за дискретизации.

т.е. модовый состав по первым L модам будет в точности требуемым, хотя моды высших порядков сохранятся. Пользуясь рядом Неймана при

I1НТ || < 1                                                                                                (56)

операцию (55) с большой степенью точности можно представить в виде ряда

в(р) - В. + Е (-Н*)ГВ.

L L r=0 L L или рекуррентными соотношениями [5]

g^^ = ст . ст (^ ^ = (-Н*)^(Г~^       • г = 1                                     (57)

При выполнении операции коррекции порядка р я (р) = (Е + Н*)Вт(р> = (В + Н*) Е (-Н*)г s = Ге + (-l)P нр+1]* S . (58) Ju                Ju         -u                     lu Ju         » Ju Ju 1 JU                      Ju I r=0                 L                    J

Равенство (58) заменяет (26). Соответственно формула (44) для критерия 62 при нимает вид

= (р)2 _ 12tj2*lLLl^^

где

-RjTp) = (-l)P[Hp+1 + H*p+1] + (HLH*)P+1,                                  (60)

Hp+1 + H*p+1

e^(p) = i ₊ (-d^p -----²------^F .                             ₍₆₁₎

Заметим, что при p=0 формулы (57)-(61) переходят соответственно в формулы (41)-(44), (30).

• 6, Дискретизация в оптических элементах, согласованных с модами Гаусса-Эрмита

Для ортонормированных мод Гаусса—Эрмита [7], имеющих комплексную амплитуду

Фр1(х,у) =Фр(х)Ф1(у), где_

ф (х) = Еп И ( д2х )ехр(- тМ , р        Ор р оо

max

производная может быть представлена выражением

Фр (х)

следующим из рекуррентных соотношений полиномов Эрмита Нр(•) [8]. Соотношение (65) и свойство ортонормированности функций (62) позволяют получить простые вы ражения для матричных элементов возмущений. В случае плоской освещающей волны (Е(х) = 1) Формулы (пЮ) , (п14) приложения дают

Qd1d • i • = -^т   6i J < ^рр ' + /Tp^THFTij) б

Р±Р х 12N2                               РР

- /р(р’+1) 6р_2,р, - /(р+1)р' 6p+2fpl] +

+ 6рр, (/11' + /(1+1) (1'-1) 6ц, - /1(1’+1) 61-21,

/(1+1^1’ 61+2,1'

Hplp'1'

= -Qplp'l' + [51ПС sinc(^-) - cos(jS-)

2n/Nv

(^ sine (A) v Nv slnc ^ *

1 6    ,

PP

6ц, +

* ^I’t*^ ⁶p+l,p* ~ ^/p’^{+1 6}p-1,p'] *

+ sin (^4 v где sinc(E) = S~n ™ £ ,

Na = §,(68)

Nv = l/vx 6, Nv = l/vy 6 ,(69)

Величины N^, N^, N^ показывают, сколько элементов разрешения укладываются соответственно на радиусе о основной моды, на периоде несущей по оси х и по оси у.

Рассмотрим пример. Пусть изготавливается оптический элемент размера di=d2=d, формирующий лишь одну моду Гаусса-Эрмита с параметром о, из плоской освещающей волны. Используется способ фазового кодирования с несущей v^ = v, vy = 0. Задано разрешение 6.

Учитывая, что

Wmax < .     = 1 /2(70)

Epi max о п по формулам (49)-(52), (32), (34) и (6б)-(69) получаем следующие расчетные соотношения (^ = 1)

6Фр1 2^ sinc n ^ + In2 2 г                  Vо

w л2

” 3N26N^

V о

Z1^1” н^1- [sinc S пад пад 1 v

р 4-14-1]

6N^ I z о J

где

1= (^) ^2

12 а

- энергетическая эффективность модовых оптических элементов в отсутствие дискретизации .

При 6* имеем N^ -* °0, N^ - 0. При конкретном б > О первые слагаемые в (71) и (72) описывают погрешность дискретной передачи несущей, а вторые слагаемые погрешность дискретного представления модовой функции дены значения критериев (72), (71) ,

ф 1 • pl

В табл. 1,

2 приве-

Таблица 1 Коэффициент снижения энергетической эффективности из-за дискретизации е"^^¹ (N = 4)

р+1	1                       }                      i 0     ;     5     ’   10 ।                      j                      ।			। 50    {   100 т
5	0,797	0,740	0,684	0,318	0,053
10	0,807	0,792	0,778	0,664	0,536
20	0,810	0,806	0,804	0,785	0,762
30	0,810	0,808	0,807	0,794	0,776

Таблица 2

Зависимость характеристик модового элемента от несущей пространственной частоты (N^=10, р+1=10)

С ростом порядка (р+1) моды ф

pl

энергетическая эффективность е

1др1у/епад

падает, а среднеквадратичное уклонение 6^ растет. Задаваясь допустимым спадом

энергетической эффективности и максимальным значением среднеквадратичного укло

нения       получим оценку максимального порядка моды,

Фтах на изготавливаемый оптический элемент.

которую можно записать

(р+1)     = min(p1, p2)z max

где pi = 6N^[sinc(^-) - /1 - х] - 1,

Ра = 6N2[б^    -2(1 - sine ^-)] - 1

oL Фтах

Следует также учитывать ограничение ширины моды -с/р+0,5

* а /1+0,5

раз

мером оптического элемента, порождающее оценку

d 2    1

р £ р₃; 1 < р₃; Рз = ⁴<2о>  * 2^е

N V	2	4	6	8	10	20
е1др1 е1р1	0,374	0,777	0,868	0,913	0,924	0,954
6фр1	0,758	0,218	0,118	0,070	0,058	0,028

Так, при х = 0,2, Nv = 6^ = 0,2, d = 5 мкм, 6 = 25 мкм получим Р + 1 S 21 при N = 26 и р+1 < 2 при N =  10.

С ростом несущей пространственной частоты v (т.е. с уменьшением N^) энерге тическая эффективность е

1др1

(72) падает, а среднеквадратичный критерий увели

чивается, т.е. одновременно

происходит улучшение качества формируемого распре

деления комплексной амплитуды и растет доля падающего на него светового потока.

Таким образом, при наличии дискретизации следует минимизировать пространст венную частоту v. Следует однако иметь в виду, что нижняя граница v определяется условиями разделения нулевого и первого порядков.

ПРИЛОЖЕНИЕ

Оценка матричных элементов возмущений

Оценим матричные элементы Нр^рце' Qpip’i*

(20), (37) для Е(х)

const (плос-

кая освещающая волна). Для v = 0 элемент Hpip•х• оценивался в работе [4]. Обобщим предложенный в [4] метод.

Возмущения дискретизации (19), (18) являются кусочными функциями, имеющими различные параметры в различных ячейках разрешения Gnm. В силу малости разме- ра б ячейки можно разложить ф

(х) в ряд Тейлора с центром х^ и ограничиться линейными членами:

Ф (х) = (х ) + (х-х )7ф -. (х ) , х CG . pl       pl nm        nm pl пт       пт

Подставляя (п!), (18) в (19) получаем bpl^ = ^l^nm1 (ехрИгп^^-^)] - 1} - (х-хпт)7фр1 хпт при х € G пт

Теперь можно оценить матричные элементы (20)

11 = ^               1 (x)d2 х = Е / ^х)Ф । (x)d х .

р F G р р              n,m G р р пт

Подставляя (п!), (п2) в (пЗ) и учитывая, что

/ (х-х )d2(x)=0,

G nm

/   (х-х)2d2 x = /   (yy_)2d2 x =, nm nmnm

(nl)

(n2)

(пЗ)

(п4)

(п5)

(пб)

/    (х-х__) {ехр [+12тгу (х-х ) 1 — 1} d2 х = 162F (v ,v ,6),

(n7)

_         nm L           nm J                      x у nm sin nt где sinc(t) = —^—

,v ,6) у

Fo(v ,v ,6)

Fo (vx,vv,6)\

Fo(v ,V_v,^V sine(v 6) - cos(ny 6)

X

2nv x

- sine(^уб)

(n8)

(n9)

Hplp'l' - 62n=m ^l^nm’^1!'^ lsinc^        - 1] +

+ ^l^nm’ ^p'l'^nm^x'V61 ~ ^l^^p'l'^nm* S ’

Аппроксимируя интегральную сумму интегралом и учитывая ортонормированность функций ф (х) получаем

^Hplp'l' ⁼~ Т2 ^J_G VФ*₁(x)Vф_plll(;)d²x

+ iF(v ,v ,6) J Ф*.(x)7ф ,.,(x)d²x

(nlO)

(nil)

Для вычисления матричных элементов Qp^pi^i (37) воспользуемся формулой (18) (Е(х) = const). Производя интегрирование имеем

°Р1 Р'1' - 6РР'6И' - 6" = ^l^nm'l-p'l’Snm’-

С другой стороны, условие ортонормированности модовых функций с учетом (п1) и (п4) , (п5) принимает вид

6ПП,611' = ^ Ф*1<х)ф ,., (x)d2x = Е /   ф*1(х)ф (x)d2x =

РУ XX    G рх    р х           n Gрх р X пт

= 62n=m фр1 ^nm^p'l'^nm1 + 12 Д 7фр1 ^ 7 фр'1' ^nm1 •           ,п1

Подставляя (п!2) в (nil) получаем hplp'l' -TS^^l’-nm'Wp'l''^

(л13)

Аппроксимируя сумму в (п13) интегралом окончательно записываем результат

Qplp'l' = Й 7фр1(5) %'!' (x)d=x.                                 (п14)

Формулы (п!0) , (п!4) позволяют оценивать матричные элементы возмущений, встре чающиеся при изучении дискретизации в основной части работы.