Дискретная модель связанных нелинейных осцилляторов

• 1.    В работе [1] предложен метод численного моделирования нелинейных колебательных систем, основанный на использовании импульсного отклика линейного резонатора для дискретизации времени в уравнении движения системы. Метод ориентирован на нелинейные колебательные и автоколебательные системы с одной степенью свободы. На практике реальные радиотехнические системы могут содержать несколько резонаторов или описываться осцилляторными моделями высоких порядков. Это, например, многокаскадные резонансные усилители и автогенераторы [2], в том числе кольцевые [3], автогенераторы, стабилизированные дополнительными резонаторами [4], и другие радиосистемы.

• 2.    В качестве дифференциальной модели М связанных осцилляторов с вектором состояния u = ( U i , U 2, ^ U m ) рассмотрим систему уравнений движения

В настоящей статье метод работы [1] обобщается на случай многоконтурных нелинейных колебательных и автоколебательных систем. Предлагаемый подход легко сочетается с методами цифровой обработки сигналов.

d2 u    to du™    2        2 z Г du)

—m +_ m—m + to² u = ю™ f u ,   ,   (1)

m m mm dt2   Qm dt                  V dt)

где to _m — собственные частоты осцилляторов; Q_m — их добротности; f_m ( u , d u / dt ) - функции, описывающие связи и нелинейности в системе осцилляторов.

Альтернативной (1) формой описания колебательной системы является ее интегральная модель в виде системы уравнений Вольтерра второго рода:

t

U m ( t ) = J f m ( U, U ) h m ( t - t) d T + U m ( t ),         (2)

где функции времени U_m ( t ) описывают свободные колебания в резонаторе, а ядра h_m ( t - t) —

импульсные характеристики осцилляторов, удовлетворяющие уравнениям

d ² h_m dt ²

+

^to m h mm

Q m dt

+ to mhm

= tom 5( t)

с дельта-функцией в правой части и нулевыми начальными условиями. Решениями уравнений (3) при t > 0 являются функции

h m ⁽ t )   ^to m

exp

^{to m} t sin(to, t ).

2 Q m ) m

При этом предполагается, что осцилляторы имеют высокие Q_m > 10 добротности.

Нетрудно установить, что отсчеты импульсных характеристик (4) на равномерной временной сетке t n = n A t при n > 2 удовлетворяют разностным уравнениям

D 2 ^{{ h}m ⁽ t n ^{) } _} h m ⁽ t n )

^- 2^a m ^{cos( to} m ^A t^{) h}m ⁽ t n - 1 ) ^{+ a} m i h m ⁽ t n - 1 ) = ⁰

с начальными условиями h_m ( t q) = h_m (0) = 0, h m ( t 1 ) = h m (A t ) = a m to m sin(to m A t ), где

I to a = exp--— At m I 2 Qm

Последовательности отсчетов применим h_m ( t_n ) при переходе к дискретному времени в интегральном уравнении (2). Для этого создадим совокупность дискретизирующих последовательностей

u m ⁽ t 2 ) = ^{1 A th}m ^{( A} t ) f m ( ^u 0 , ^u 0 ) ⁺ U m ⁽ t 1 ), u m ⁽ t 2 ) = ^{A th}m ^{(2 A} t ) f m ( ^u 0 , u 0 ) ⁺ U m ⁽ t 2 ).

to hm (t) = At £hm(tk)5(t - tk).                    (6)

k = 0

Импульсные характеристики hm (t - т) в (2) заменим последовательностями (6). После интегрирования для значений решения на временной сетке tn получим систему уравнений дискретной свертки um(tn) =

3. Рассмотрим пример – нелинейный резонанс в связанных осцилляторах Дюффинга. Осциллятор Дюффинга является базовым объектом классической теории колебаний [5] и, в то же время, может служить моделью реальных радиосистем, например, колебательного контура, перестраиваемого варикапом [6].

Исходная система уравнений движения идентичных реактивно связанных осцилляторов с собственными частотами to o и Q имеет вид

d ² U

dt ²

to₀ dU

Q dt

+ to2 U =

n

= ^A t £ f m ( ^{u (} t k )> ^{u (} t k ) ) h m ⁽ t n ^- t k ) + U m ⁽ t n )• k = 0

= -цtoOU3 + KtoO (V - U) + tooS(t),

d ² V dt ²

to 0 dV

Q dt

+ to2 V =

Теперь обе части уравнений (7) подвергнем воздействию разностных операторов D 2 ( 0 } . При n > 2 это приводит к следующему результату:

D 2 { u m ⁽ t n ) } =

= A th m (A t ) f m ( u ( t n - A t ), u ( t n - A t ) ) .

Отметим, что в процессе преобразования правой части (8) использованы уравнения (5) и аналогичные им уравнения D 2 { U_n ( t_n ) } = 0, а также равенства h_m (0) = 0. Следует обратить внимание на то, что равенства h_m (0) = 0 приводят к зависимости правой части (8) от момента времени t_n - A t = t_n - 1 и позволяют получить явный алгоритм моделирования автоколебаний при аппроксимации производных u ( t_n - 1 ) левыми разностями. Ограничиваясь трехточечной аппроксимацией, имеем

^{3 u (} t n - 1 ) ^{- 4 u (} t n - 2 ) ^{+ u (} t n - 3 )

2A t                 ■

^{u (} t n - 1 ) =

Таким образом, алгоритм моделирования колебаний в системе связанных нелинейных осцилляторов задается системой рекуррентных соотношений um(tn ) 2am cos(tom At)um(tn-1) +

+ ^a m u m ⁽ t n - 2 ) = ^{A th}m ^{( A} t ) f m ^{( u (} t n - 1 ), ^{u (} t n - 1 ) ) ,

где n = 3,4,..., а значения u_m ( t 1 ) и u_m ( 1 2 ) в соответствии с интегральными уравнениями (2) определяются по начальным условиям U o, u 0 с помощью выражений

= -цtoOV3 + Kto2 (U - V).

Здесь ц и к — параметры нелинейности и связи; S ( t ) – сигнал внешнего воздействия на один из осцилляторов.

При проведении расчетов собственную частоту to₀ будем измерять в единицах частоты дискретизации to d = 2п / A t : Qo = to o / to d , а также введем обозначения

X = h(At)At = nQo exp I -

Qo

2 Q

и U_n = U ( t_n ), V_n = V ( t_n ). Тогда алгоритм моделирования (10) для системы уравнений (11) примет вид

U_n - 2a cos(2nQ₀) U_n - 1 + a² U_{n - 2} =

= 2X sin(2nQo) x

х ( -ц U n - 1 +k( V n - 1 - U n - 1 ) + S n - 1 ) ,           (12)

V n - 2a cos(2nQ o ) V n - 1 + a² V n - 2 =

= 2X sin(2nQ o ) ( -ц V ³- 1 + k( U n - 1 - V n - 1 ) ) .

Для оценки достоверности результатов моделирования колебаний в связанных осцилляторах Дюффинга применим разностную схему (12) к расчету амплитудно-частотных характеристик (АЧХ) линеаризованной системы, положив в (11) и (12) ц = 0. Эта задача имеет точное решение — на рис. 1 АЧХ K 1 (Q) и K 2 (Q) первого и второго осцилляторов показаны непрерывными линиями (параметры системы: Qo = 0.1, Q = 20, к = 0.06).

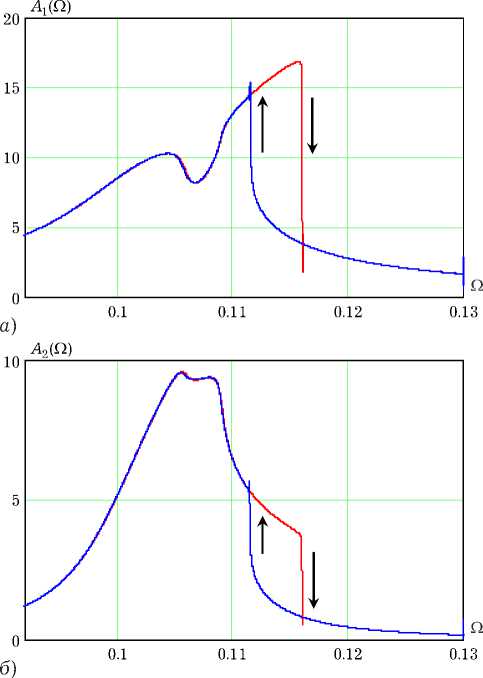
Рис. 2. Частотные зависимости амплитуд колебаний связанных осцилляторов Дюффинга

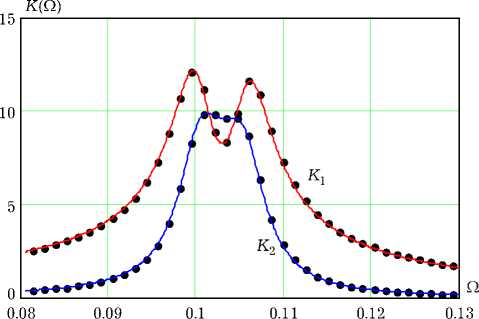
Рис. 1. АЧХ связанных линейных осцилляторов

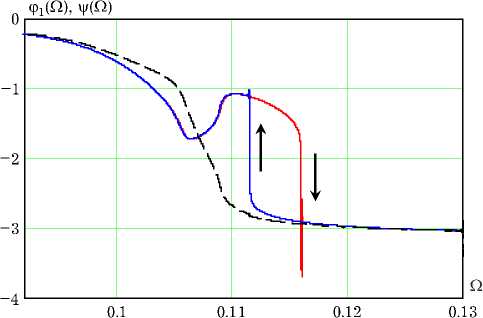
Рис. 3. Частотные зависимости фаз колебаний связанных осцилляторов Дюффинга

Точками на рис. 1 показаны результаты расчетов АЧХ с помощью разностной схемы (12). При этом амплитуды оценивались путем квадратичного усреднения установившихся реализаций вынужденных колебаний:

• A U =2 U ² n _N , A V =2 V n ² _N .

• 4 .    Представленный здесь численный метод предназначен для моделирования нелинейных осцилляторных систем. Метод имеет второй порядок точности по дискретному времени, сохраняет форму импульсных характеристик осцилляторов и хорошо стыкуется с алгоритмами цифровой обработки сигналов.

Графики демонстрируют хорошее согласование численных и точных аналитических результатов.

Перейдем теперь к моделированию с помощью (12) связанных осцилляторов Дюффинга. Ряд ре- зультатов для системы с параметрами Ω0 = 0.1, Q = 20, κ =0.06, µ = 0.0012 при единичной амплитуде внешнего воздействия S(t) представлен ниже в виде графиков.

На рис. 2 показаны графики зависимостей амплитуд первых гармоник вынужденных колебаний в первом ( а ) и втором ( б ) осцилляторах от частоты внешнего воздействия. Оценки амплитуд проводились методом аналитического сигнала в численных экспериментах с квази-статической перестройкой частоты в диапазоне 0.09 ≤Ω≤0.13. При этом третья гармоника колебаний удалялась с помощью фурье-фильтрации. Как следует из графиков, частотные зависимости амплитуд характеризуются скачками и гистерезисом. Стрелки на графиках указывают направления скачков при изменениях частоты в сторону повышения или понижения. Выбросы в конечных точках скачков обусловлены затухающими свободными колебаниями.

Фазовые соотношения в связанных осцилляторах Дюффинга иллюстрируют графики, приведенные на рис. 3. Сплошной линией показан график частотной зависимости ϕ1(Ω) разности фаз колебаний в первом осцилляторе и вынуждающих колебаний. Зависимость характеризуется скачками и гистерезисом. В то же время, частотная зависимость ψ(Ω) разности фаз колебаний во втором и в первом осцилляторах – гладкая функция без скачков.