Дискретность спектра оператора Лапласа - Бельтрами и преобразование метрики многообразия

В работе доказывается свойство сохранения дискретности спектра оператора Лапласа — Бельтрами на простых искривленных произведениях порядка k при специальном квазиизометричном преобразовании метрики этого многообразия. Сделаны некоторые замечания о случае оператора Шредингера.

Главным объектом исследования в данной статье является оператор Лапласа — Бельтрами —4 = —divV на некоторых многообразиях специального вида. Для начала рассмотрим риманово многообразие Z, изометричное произведению X × Y (где X — произвольное многообразие размерности n, а Y — компактное размерности m) с метрикой dz2 = dx2 + y 2(x)dy2, где y(x) — C 1 -гладкая положительная функция, dx2 и dy2 — метрики на X и Y соответственно, то есть dx2 = ^^aij (x)dxidxj, dy2 = ^bki (y)dyk dyi.

Следовательно, метрический тензор на Z имеет вид kgstk =

IK- ^(x) k          ⁰

0       Y2(x)kbki(y)k а определитель G = det kgstk = det ||gstk-1 = y 2m(x)A(x)B(y), где мы обозначили A(x) = det ||aijk, B(y) = det kbki|.

Будем предполагать, что метрика kg _st k многообразия Z претерпевает изменения, описываемые матрицей a(x) , у которой все отличные от нуля элементы стоят на главной диагонали и она имеет вид

IHx)k =

r’ . ( x )	0
0	^ 2 L x )

,

* Работа выполнена при поддержке гранта РФФИ № 10-01-97004-р_Повольжье_а.

где k^ 1 (x)k — тоже диагональная матрица c C 1 -гладкими коэффициентами, ||o ₂ (x)k = 0 22 (x)E m (здесь 0 22 (x) — C 1 -гладкая положительная функция, E m — единичная матрица m х m ). Обозначим через S(x) = det k^(x)k = det ||a 1 (x) ka ₂2^m (x) , через p = o g — произведение матриц o(x) и g(x) , соответственно, определитель этой матрицы P = det kp ij|| = y ^2m (x)A(x)B(y)S(x) .

Оператор Лапласа — Бельтрами при таком изменении метрики преобразуется следующим образом:

—A = - -L div(VSo - 1 V) = 4= ^y 4 ( Vp p j 4).

Vs            VP. ^9z?  ^r dzj'

i,j=1                   j

Докажем следующую лемму о его представлении на таких многообразиях. Введем для этого еще одно обозначение r = o 1 a — произведение матриц o 1 (x) и a(x) и его определитель R .

Лемма 1. Оператор Лапласа — Бельтрами —А после описанного преобразования метрики на многообразии Z принимает вид

—AZ = A0 + 02 2(x)Y 2(—ay ), где A0 — оператор Лапласа — Бельтрами на многообразии X с метрикой, преобразованной матрицей o1 (x) и с мерой плотности d2m (x)ym (x):

A 0 ⁼

O 2^m (x)Y ^m (x) pR(x)

m

(x)Y ^m (x) VR(x)r ^ij

∂x j

а —A Y — оператор Лапласа — Бельтрами на многообразии Y:

—Ay =

VW)

m

k,l=1

Доказательство. Сначала исследуем структуру матрицы p :

kp rp k = ko ki kkg st k =

MxM

0 (? 2² (x)E m

|a ij (xM

Y 2 ^{( x ) k}b ki ⁽ y ^{) k}

^{k o} i ^{( x ) kk}a ij ^{( x )} k 0

0 _________

(° 2^{2 (x)}Y^{2(x) kb} ki ⁽ y ^{) k}

kr ij ( x ) k	0
0	° 22 ( x ) Y 2 ( x ) kb kl ( y ) k

,

следовательно, обратная матрица имеет вид:

kp rp k =

kr ij ^{( x ) k} I „          ⁰

0       O2-2(x)y-2(x)kbkZ(y)k где krij(x)k = kaij(x)kkoi 1(x)k.

Теперь, исходя из координатной записи оператора Лапласа — Бельтрами после изменения метрики многообразия Z , преобразуем его до требуемой формы:

-N z ^—

1   n+m

* s,t=1

1 X d

∂z s,t=1 s

-

n+m

Y ^m (x) V A(x)B(y)^(x)

s,t=n+1 s                         t

n

X    (pXx) V.A . B : . r gx- i,j=1 i                                                 j

-

0"2

² (x)Y m (x)

V ^{A (x) B (}y)^^(x)

m

X Л- И №VA(x)B№(x)b^H —

∂y k                               ∂y l

n

2^{m (x}h ” (x)V^{R ( x )} jl

-m(x) VR(xK ^j

∂x j

-

o" 2² (x)Y ² (x) V B(y)

m

X д- (bW² Л —

P1 SykV        ^d

^— A ^{0 +} ■ ^{( - Л у} )•

Лемма доказана.

Теперь перейдем к рассмотрению спектра оператора Лапласа — Бельтрами на этом многообразии при описанном преобразовании метрики.

Теорема 1. Оператор Лапласа — Бельтрами на многообразии X × Y , метрика которого преобразована матрицей ka(x)k , имеет дискретный спектр тогда и только тогда, когда дискретен спектр оператора А ₀ (оператора Лапласа — Бельтрами) на многообразии X с метрикой, преобразованной матрицей ^(x) и с мерой плотности cf ₂ ^m (x)Y m (x).

Доказательство. Заметим, что, поскольку речь в данной теореме идет об изменении метрики, нам будет удобнее обозначать рассматриваемое многообразие тройкой (X х Y, g , v ) , где v — мера на многообразии, совпадающая с римановым объемом. Тогда, после изменения метрики матрицей ||a (x)k , объектом рассмотрения становится многообразие (X х Y, p, v ) . Относительно этого многообразия справедлива теорема 1 из [2], в соответствие с которой дискретность спектра оператора Лапласа — Бельтрами на многообразии (X х Y, p, v ) эквивалентна дискретности спектра оператора Лапласа — Бельтрами на многообразии (X, г, ^) , где ^ — мера на многообразии X плотности a ₂ ^m (x)y ^m (x) . Заметим, что этот оператор есть оператор А ₀ , описанный предыдущей леммой, а само такое многообразие можно рассматривать как многообразие (X, а, ^) , метрика которого преобразована матрицей |a ₁ (x)| . Так как а — исходная метрика многообразия X , опуская ее, получаем утверждение теоремы.

Далее рассмотрим полное риманово многообразие D — простое искривленное произведение порядка k, то есть многообразие, изометричное произведению R+ x Si x S2 x ••• x Sk (где R+ = (0, +to), a Si — компактные римановы многообразия без края, dim Si = ni) с метрикой ds2 = dr2 + q2(r)d92 + • • • + q2(r)d02, где d62 — метрика на Si, а qi(r) — C 1-гладкие положительные на R+ функции. Обозначим s(r) = q^1 (r) ••• q^k (r). Пусть преобразование метрики на этом многообразии задается матрицей a(r) следующего вида:

k^ ( r ) k =	5 2 ( r )	0      ...      0
	0	S 2 (r)E n i ...       0
	. . .	.. .. ..
	0	0       ... d 2 ( r ) E n k

Все коэффициенты этой матрицы полагаем C ¹ -гладкими, а ее определитель будем обозначать, как и выше, S(r) . Для описанной матрицы его, очевидно, нетрудно вычислить:

=(r) = det |Hr)ll = 5 2 (r)i 2" 1 (r) ••• - (r).

Оператор Лапласа — Бельтрами при таком изменении метрики преобразуется следующим образом:

—А = — —= div (V=a ^-1 V).

Теорема 2. Спектр оператора нена одна из групп условий:

—А дискретен тогда и только тогда, когда выпол-

∞ j p=(t)s(t)dt < to,

I)

r lim r→∞

8 2 ^(t)

V=t)s(t)

∞ dt j p=(t)s(t)dt = 0;

r

или

∞

Г 5² (t)      ,

—.    ---dt <  to ,

1 VWMt)

II)

∞ lim / r →∞

r

5 0 (t)

V=t)s(t)

r dt j p=(t)s(t)dt = 0.

Доказательство. Обозначим через g метрику на многообразии D . Тогда после преобразования этой метрики матрицей ||a (x)k мы получим на многообразии D новую метрику p = а д . Учитывая, что матрица ||a (x)k — диагональная, эту метрику легко записать в дифференциальной форме:

dZ ² = 5 o2 (r)dr ² + 5 1² (Ф 2 (гИ 2 + ••• + 5 2 (r)q k (r)d<

Но тогда —А — обычный оператор Лапласа — Бельтрами на многообразии D с описанной метрикой p , и для него справедлива Основная теорема из [2]. В соответствии с этой теоремой и введенными выше обозначениями имеем, что спектр оператора —А на многообразии D дискретен тогда и только тогда, когда выполнена одна из групп условий:

∞ j p/X(l)s(t)dt < то, 0

и

∞

lim [ d 2 (t)PS ^-1 (t)s ^-1 (t)dt [ P ^(t)s$(t)d,t r →∞

= 0,

1r

либо

∞

J 5 2 (t) pX ^-1 (t)s ^-1 (t)dt < то,

и

∞ r

lim [ 5 2 (t)PX ^-1 (t)s ^-1 (t)dt [ P X(t)ss(t)d,t r →∞

= 0.

r

Что и утверждает теорема.

Заметим теперь, что для того чтобы матрица а(г) описывала квазиизометричное преобразование метрики, нужно потребовать (см., например, [1]), чтобы она удовлетворяла следующим условиям для некоторой константы а >  1 :

а ¹ |(| 2 6 (а(,() g 6 а|(| ² , для всех £ G TD

и а- 6 X(r) 6 an.

Если теперь в условии (1) мы будем выбирать векторы ξ такие, у которых лишь одна координата ненулевая, то из него мы немедленно получим, что а 1 < 52(r) < а для всех i = 1,..., k.

А из этого условия неравенство (2) следует автоматически.

Следствие 1. Если на многообразии D оператор Лапласа — Бельтрами —А имел дискретный спектр, то при квазиизометричном изменении метрики многообразия D диагональной матрицей ka(r)k спектр оператора Лапласа — Бельтрами —А останется дискретным. Аналогично, недискретный спектр останется недискретным.

Доказательство. Введем обозначения:

r

W (r)

=/ sdt)

∞

∞

r

r

W (r)

dt

J sm

r

s(t)dt.

Из условия (3) имеем следующие оценки:

α

∞∞ n/2 I s(t)dt < I V^(t)s(t)dt < an/2

∞

I s(t)dt, 0

r

∞

a ^-n-1 W (r)

< J 5 2 (t)pS 1 (t)s ¹ (t)dt j p^(t)s(t)dt

< a ⁿ⁺¹ W(r),

r

α

-

∞ d <

∞

∞∞

I <^(t) c            < a ^1+n/2

s ^-1 ( t ) dt,

r

^n-1 W(r) <  15; 2 (t) V E-4t)s-¹(t)dr I V^(t)s(t)dt < a ⁿ⁺¹ W(r).

r

Из этих оценок очевидно следует, что если на многообразии D было выполнено какое-то из условий Основной теоремы из [2], то непременно будет выполнено и соответствующее условие теоремы 2. Обратно, если ни одна из групп условий Основной теоремы из [2] не была справедлива на многообразии D , то не будут выполнены и условия теоремы 2. Таким образом заключаем, что свойство дискретности спектра не изменяется при специального вида квазиизометричном преобразовании метрики, описанном матрицей IH^x)||.

В заключение отметим, что совершенно аналогично проводится исследование дискретности спектра оператора Шредингера L = —А+ c(r) при преобразовании метрики на многообразии D . Для формулировки этого результата введем следующие обозначения:

где d(r) =

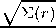
6 o (r)

F ^{( r )} = ^{c ( r )} + s^Tr^

²⁶⁽¹ )

+

+

s ⁰ (r)

2s(r)

s ⁰ (r)5 0 (r)

2s(r)5(r)

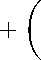
5'(r) у

25(r))

Тогда, используя в приведенных выше рассуждениях теорему 2 из [3],

получаем следующую теорему.

Теорема 3. Если F(r) + Ф(г) > —C (C = const > 0), то для дискретности спектра оператора Шредингера L на многообразии D необходимо и достаточно, чтобы для произвольного ш > 0 было выполнено r+ш lim r→∞

I (F (r) + Ф(r))dr =+то. r

Далее, по аналогии с рассуждениями для оператора Лапласа — Бельтрами, можно получить следствие из данной теоремы о сохранении свойства дискретности спектра оператора Шредингера при квазиизометричном преобразовании метрики. Однако в этом следствии необходимо требовать, чтобы функции F (r) и Ф(г) обе были ограничены снизу, а это очень жесткое требование, поскольку даже при квазиизометричном преобразовании метрики функция Ф(г) может оказаться неограниченной, и никаких выводов о сохранении свойства дискретности спектра сделать будет невозможно. Поэтому результат для оператора Шредингера в данном случае менее интересен, чем для оператора Лапласа — Бельтрами.