Дискретные отображения томсоновских автоколебательных систем с запаздыванием

Модели с запаздывающими обратными связями (ЗОС) широко используются в исследованиях автоколебаний в радиочастотном [1; 2], микроволновом [3; 4] и оптическом [5] диапазонах и имеют множество других физических приложений (см., например, [6]).

Автоколебательные системы (АКС) с ЗОС часто характеризуются более сложной динамикой, чем классические АКС, в частности, они легко переходят в режимы генерации динамического хаоса [7–10]. Сложная динамика в не меньшей степени присуща и системам, осциллирующим в дискретном времени (ДВ) [11]. В связи с этим ДВ-АКС с ЗОС представляют интерес как объекты исследований в рамках нелинейной динамики с дискретным временем, а также как источники радиосигналов сложной формы.

Способ перехода к дискретному времени в аналоговых моделях АКС в конечном счете существенным образом влияет динамические характеристики синтезированных ДВ-систем (дискретных отображений) [12]. В настоящей работе для проектирования дискретных отображений аналоговых АКС томсоновского типа с ЗОС использован метод структурного синтеза в сочетании с принципом инвариантности импульсных характеристик линейных резонаторов [13].

1. Структурный синтез АКС

В качестве основного прототипа в непрерывном времени выберем осциллятор с уравнением движения вида dy + 70 dy + 7° у = ю°7 dF ( у (tтП’      (1)

dt2   Q dt             dt где to° и Q — собственная частота и добротность резонансного контура АКС; у — параметр цепи обратной связи с нелинейностью F(ут) и временем запаздывания т. Формально при выполнении условий Q >> 1, у << 1 АКС (1) относится к классу томсоновских.

Используемый способ проектирования ДВ-осциллятора в определенном смысле можно назвать структурным, поскольку он опирается на представление о структурной схеме томсоновской АКС (1), как кольцевом соединении блоков «резонатор – нелинейный усилитель – запаздывающая обратная связь».

Динамическую (инерционную) часть АКС (1) представляет резонансный контур с дифференциальным уравнением движения d ² y to dy о d / х

⁺ 70 77 ^{+ ю}° У = ⁷° 77 x ⁽ t ),                ⁽²⁾

dt2   Q dt            dt где x(t) – сигнал возбуждения. Контур имеет импульсную характеристику

h ( t ) = to ° exp

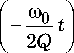
x

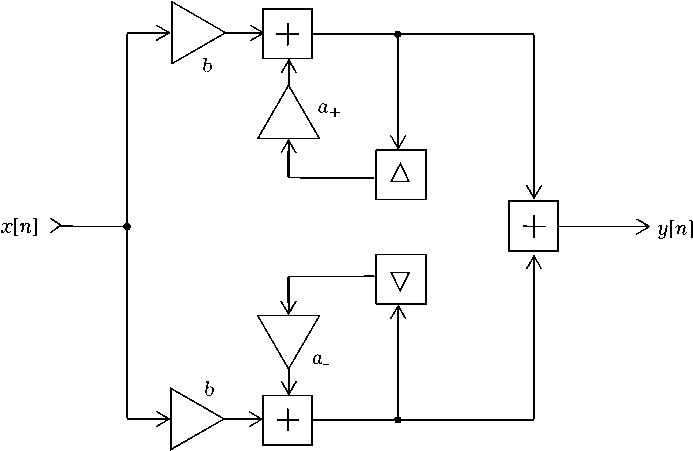
Рис. 1. Структурная схема ДВ-резонатора

cos( toi t )--,           sm( toi t )

4 Q ² - 1

® to o exp ^- ^ ° t J cos( to o t ).

Ее дискретные временные отсчеты, взятые с интервалом А , определяют импульсную характеристику ДВ-резонатора:

h [ n ] = А ■ h ( t n ) = 2 nQ o a ⁿ cos ( 2 nQ o n ) .          (3)

Здесь Q o = to o А /2 п — собственная частота контура, измеряемая в единицах частоты дискретизации to d = 2 п / А ; a = exp ( -nQ o / Q ) — параметр диссипации.

Так как частотная характеристика ДВ-систе-мы связана с ее импульсной характеристикой дискретным во времени преобразованием Фурье [13]:

H(jQ) = £ h[n] exp (-j2nQn), n=0

то для (3), проведя вычисления, получим

H ( j Q ) = H + ( j Q ) + H - ( j Q ) =

=--------- 7 ---^nQ 0----- 7 ------7 +              (4)

• 1    - a exp ( j 2 nQ o ) exp ( - j 2 nQ )

• ₊___________ ^nQ 0 ___________

• 1    - a exp ( - j 2 nQ o ) exp ( - j 2 nQ )

Эта частотная характеристика соответствует системе разностных уравнений движения вида

У [ n ] = У + [ n ] + У - [ n ],

У + [ n ] = a + У + [ n - 1] + bx [ n ],                       (5)

У - [ n ] = a - У - [ n - 1] + bx [ n ]

с коэффициентами a + = a exp (j2nQo), a - = a exp (-j 2nQo), b = nQo .

Отметим, что a - = a + , поэтому при действительном сигнале у [ n ] осцилляции у - [ n ] комплексно сопряжены но отношению к y ₊ [ n ]: y - [ n ] = y + [ n ].

Уравнения движения (5) наглядно отображаются блок-схемой ДВ-контура в форме параллельного соединения блоков первого порядка, представленной на рис. 1.

В автоколебательной системе с уравнением движения (1) роль сигнала возбуждения x ( t ) играет сигнал на выходе нелинейного усилителя, вход которого через ЗОС связан с выходом контура y ( t ):

x ( t ) = Y F ( У ( t - т ) ) = Y G ( y ( t - t ) ) y ( t - t ) .         (6)

С учетом этой связи система разностных уравнений движения томсоновского ДВ-осциллятора с ЗОС принимает вид

У ^{[ n ]} = У + ^{[ n ]} + У - ^{[ n} 1,

У + [ n ] =

= a exp ( j 2 nQ o ) y ₊ [ n - 1] + nQ o y F ( y [ n - d ] ) ,   (7)

У - ^{[ n ]} =

= a exp ( - j 2 nQ o ) y - [ n - 1] + nQ o Y F ( y [ n - d ] ) .

При этом считается, что запаздывание составляет целое число интервалов дискретизации: т = dА. Уравнения (7) отображает блок-схема на рис. 2. При использовании операции комплексного сопряжения система (7) преобразуется к виду y [ n ] = 2 Re { y + [ n ]},

У + [ n ] =                                                (8)

= a exp ( j 2 nQ o ) y ₊ [ n - 1] + nQ o y F ( y [ n - d ] ) .

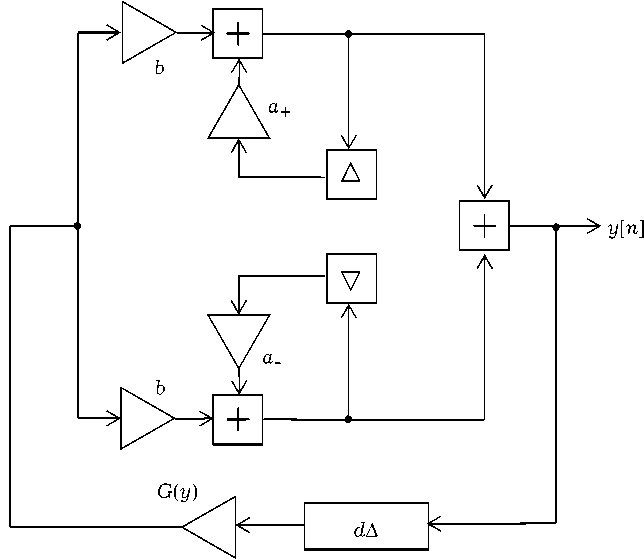
Рис. 2. Структурная схема ДВ-автогенератора (параллельная форма)

Рис. 3. Структурная схема ДВ-автогенератора

Сформированное таким образом нелинейное разностное уравнение (8) представляет собой комплексную форму уравнения движения (дискретного отображения) томсоновской ДВ-АКС с запаздывающей обратной связью.

Для перехода к действительной форме отображения правую часть выражения (4) приведем к общему знаменателю. Получим

где коэффициенты am , bk связаны с параметрами контура (2) соотношениями a1 = 2a cos (2nQo), a 2 =-a2,

Ьо = 2лП0, Ь1 = -2nQ0a cos (2лП0).

Частотная характеристика (9) описывает линейный ДВ-резонатор с разностным уравнением

H ( j П ) =

Ьо + Ь1 exp (-j 2nQ)

1 - а .1 exp ( - j 2 nQ ) - a 2 exp ( - j 4 nQ )

движения

y [ n ] - 2 a cos ( 2 nQ o ) y [ n - 1] + a ² y [ n - 2] = = 2 nQ o ( x [ n ] - a cos ( 2 nQ o ) x [ n - 1] ) .

Теперь, охватив резонатор (10) цепью обратной связи с уравнением (6), получим ДВ-АКС с уравнением движения

y [ n ] - 2 a cos ( 2 nQ o ) y [ n - 1] + a ² y [ n - 2] =

= 2 kQ o y ( F ( y [ n - d ]) -                          (11)

• - a cos(2 nQ o ) F ( y [ n - 1 - d ]) ) .

• 2.    Метод MMA для ДВ-АКС

АКС в такой форме отображается блок-схемой на рис. 3.

То обстоятельство, что при переходе от (8) к (11) не было сделано никаких приближений, указывает на эквивалентность этих дискретных отображений.

Отображение (8) воспроизводит в дискретном времени основные характеристики томсоновской АКС (1). Это нетрудно показать цифровым анализом генерируемых по алгоритму (8) времен- ных рядов, но мы воспользуемся здесь широко распространенным в теории нелинейных колебаний методом медленно меняющихся амплитуд (методом ММА) [14]. На ДВ-осцилляторы томсоновского типа метод ММА был распространен работах [12; 15]. Следуя им, генерируемый отображением (8) временной ряд (ДВ-автоколебания) представим в виде y +[ n] = 1A[ n ]exp( j 2nQo n) = 2 A[ n] Zn, (12)

где A [ n ] – комплексная амплитуда автоколебаний.

При подстановке решения (12) в разностное уравнение (8) нелинейную функцию F ( y [ n ] ) в его правой части в рамках метода ММА заменим первой гармоникой ряда Фурье:

F ( y [ n ] ) * 2 F ( A [ n ] ) Z n + 2 F ( A [ n ] ) Z - n .

Проведя в (8) очевидные математические преоб- разования, получим

A [ n ] = a A [ n - 1] + nQ _O y F 1 ( A [ n - d ] ) Z ₀ d + + nQ ₀ y F * ( A [ n - d ] ) Z ₀ ^{2 n +} d .

Последнее слагаемое здесь описывает высокочастотное воздействие (с периодом 7 = 1/ 2 Q o) на медленный процесс изменения (с характерным временем релаксации T r = Q / 2 Q o) комплексной амплитуды A [ n ]. Пренебрегая этим воздействием, приходим к укороченному уравнению для комплексной амплитуды ДВ-автоколебаний

A [ n ] = a A [ n - 1] + nQ _O y F 1 ( A [ n - d ] ) Z ₀ d .      (14)

Полученное разностное уравнение (14) сопоставим с укороченным уравнением для ком- плексной амплитуды автоколебаний в исходной аналоговой модели АКС с ЗОС (1). Нетрудно показать, что для автоколебаний вида z x 1                            x 1 -*Z                 . X

y ( t ) = 2 A ( t ) exp( j ® 0 1 ) + 2 A ( t ) exp( - j ® 0 1 )

уравнение движения (1) методом ММА сводится к дифференциальному укороченному уравнению d

A (t) = dt                                                (15)

= - ^ 0 A ( t ) + ^ 0 Y F 1 ( A ( t - t ) ) exP( - j ® 0 ^T ).

2 Q 2

При переходе к безразмерному времени 9 = tА-1 уравнение (15) принимает вид dA (^) = -л^0 A © + nQoY F1 (A ^ - d)) Zo d . (16)

d ^          Q

Учитывая разложение параметра диссипации высокодобротного контура в ряд по обратным степеням добротности

I    Qol

a = exp -n * 1

I Q J

-

^, Q

приходим к выводу о том, что разностное укороченное уравнение ДВ-АКС (14) реализует алгоритм Эйлера для укороченного уравнения (16) аналоговой АКС. Таким образом подтверждается сделанное нами ранее утверждение о том, что отображения (8) и (11) воспроизводят в дискретном времени основные динамические характеристики томсоновской АКС (1).

• 3.    Некоторые результаты анализа динамики ДВ-АКС

Приведем ряд результатов, полученных для дискретного отображения осциллятора Ван дер Поля с ЗОС. В этом случае функция нелинейности

^F ( y ) = ^ 1 ^- 3 y ² ^ y .

Отображение (8) и его укороченное уравнение (13) принимают вид

y + [ n] = aZo y + [ n - 1] +

I 12           )

+ nQ o YI 1 - 3 y [ n - d ] I y [ n - d ],

A [ n ] = a A [ n - 1] +

+ nQ ₀ y 1 1 - 1 A [ n - d ] 2 J A [ n - d ] Z ₀ ^d .

На рис. 4 точками приведены отсчеты ДВ-автоколебаний y [ n ], генерируемых отображением (17) со значениями Q o = 0.14 и Q = 15. Об-

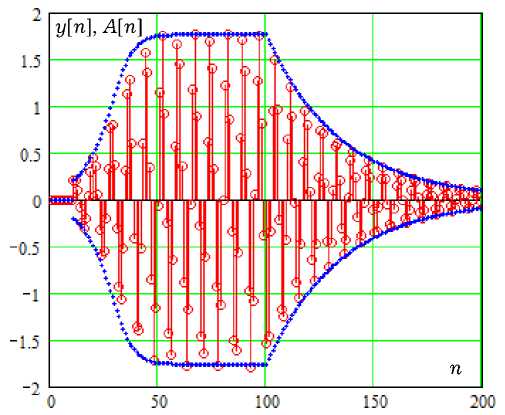
Рис. 4. Дискретные отсчеты мгновенных значений и амплитуды первой гармоники автоколебаний

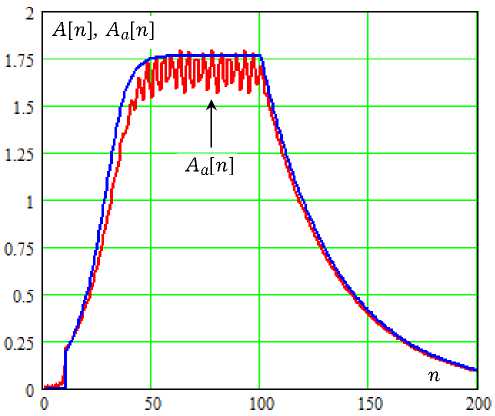
Рис. 5. Дискретные отсчеты амплитуды первой гармоники и огибающей автоколебаний

ратная связь с запаздыванием в один интервал дискретизации ( d = 1) и параметром γ = 0.45 включается на интервале времени 11 ≤ n ≤ 100. Пунктирной линией на рисунке показан график временной зависимости амплитуды автоколебаний, рассчитанный по укороченному уравнению (18). Как видно из графиков, зависимость A [ n ] с хорошим приближением воспроизводит амплитуду автоколебаний.

На рис. 5 график A [ n ] приведен вместе с графиком временной зависимости огибающей A_a [ n ] ДВ-автоколебаний y [ n ], выделенной методом аналитического сигнала с использованием дискретного преобразования Гильберта [13]. Зависимость A_a [ n ] кроме медленной кусочномонотонной компоненты содержит компоненту, осциллирующую с частотой 2 Ω ₀ . Она возникает из-за наличия третьей гармоники в спектре сигнала y [ n ]. Заметим, что осциллирующая компонента комплексной огибающей также содержится в решении укороченного уравнения (13). Это решение дает то, что в теории нелинейных колебаний носит название улучшенного первого приближения [13].

Заключение

Представленные здесь дискретные отображения томсоновских осцилляторов с запаздывающими связями расширяют круг объектов нелинейной динамики в дискретном времени, имеющих свойства аналоговых автоколебательных систем. Практические применения предложенных отображений весьма разнообразны – моделирование сигналов и систем, нелинейная фильтрация дискретных (цифровых) сигналов, защита информации (в режимах генерации динамического хаоса).