Диспергирование жидкости вихревым генератором

Генератор (рис. 1) работает следующим образом [1,2]. При подаче рабочего тела (жидкости) через входные отверстия 2 внутри вихревой камеры 3 образуется система двух закрученных потоков. По периферии камеры движется так называемый первичный вихрь I, имеющий в поперечном сечении форму кольца, состоящий из жидкости, подаваемой в генератор. Приосевую область занимает вторичный вихрь II, вращающийся как квазитвёрдое тело. Он образуется из вещества среды, в которую происходит истечение. Если природа рабочего тела и вещества окружающей генератор среды близка друг другу, то в потоке генерируются регулярные колебания давления, амплитуда которых зависит от скорости истечения и геометрических параметров вихревой камеры и сопла.

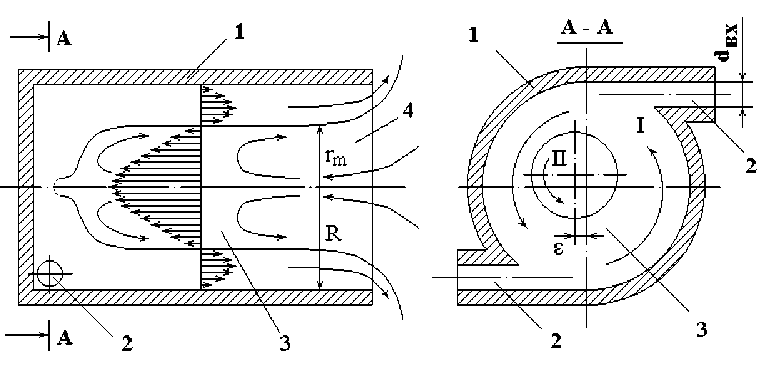
Рис. 1. Схема течения закрученного потока в камере вихревого генератора: 1 – корпус, 2 – входные отверстия, 3 – вихревая камера, 4 – сопло.

При этом наблюдаются несколько режимов работы генератора, отличающиеся величиной скорости истечения жидкости через тангенциальные отверстия (рис. 2). При небольших скоростях движения жидкости появляются гармонические колебания звукового давления малой амплитуды (рис. 2, a) обусловленные взаимодействием первичного и вторичного вихрей. При больших скоростях истечения происходит периодическое разряжение в приосевом пространстве вихревой камеры с последующим его схлопыванием. Этот процесс сопровождается звуковыми колебаниями уже не малой амплитуды.

Причём в зависимости от длины вихревой камеры и формы сопла за время движения частицы жидкости в вихревой камере возможно возбуждение звука в виде периодических звуковых импульсов (рис. 2, b) разной длительности с большей или меньшей амплитудой.

В качестве модели процесса диспергирования жидкости рассмотрим неустойчивость поверхности вязкой несжимаемой жидкости. Согласно этой модели при движении жидкости в вихревой камере на неё действует переменное давление из приосевой зоны камеры, что приводит к возбуждению поверхностных волн, нарастание амплитуды которых и ведёт к отрыву капель жидкости.

На жидкость, движущейся в вихревой камере, действуют центробежная сила инерции, которой в соответствие с принципом эквивалентности Эйнштейна можно сопоставить некоторую эффективную силу тяжести с ускорением, равным д = и ² /т, где и - скорость вращения жидкости

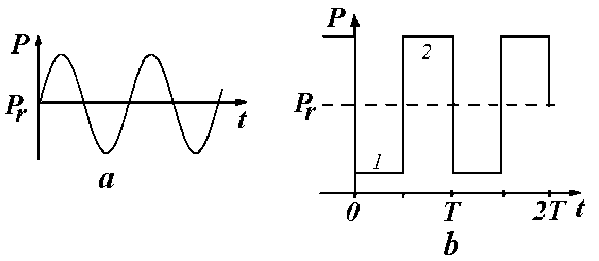
Рис. 2. Пульсации давления в вихревой камере.

в вихревой камере; т - расстояние от оси вихревой камеры до частицы жидкости в камере. Поскольку, как показано в работе [3], и « V q , то для д получаем: д = и ² /т ~ V 2 /R, где V q - скорость истечения жидкости через входное отверстие, а R - радиус вихревой камеры.

Итак, рассматривается устойчивость поверхности раздела слоёв вязкой несжимаемой жидкости бесконечной глубины, когда в верхнем слое (приосевой области) давление меняется со временем.

Задача решается в линейном по вязкости приближении методом преобразования Лапласа по времени.

Поскольку рассмотрение проводится для случая несжимаемой жидкости, то изменение давления отождествляется с изменением плотности жидкости. Предполагается, что изменение давления не влияет на кинематическую вязкость жидкости.

Равновесное состояние рассматриваемой системы запишется в виде:

V o » = 0, C o = 0, Р г = P q - P » gz,

где V = (и, у, w) - вектор скорости, р - плотность жидкости, C - смещение поверхности от положения равновесия, P q - давление на границе раздела при z = 0, г = 1,2 - номер жидкости. Жидкость с г = 1 заполняет полупространство z <  0, ас г = 2 — z > 0.

Исследуем устойчивость равновесия (1), для чего обычным образом внесём возмущения скорости и давления. Выбирая в качестве единиц измерения длины, времени, частоты, скорости и давления соответственно [а/(р 1 +р _г )д ] ^{1 / 2} , [а/(р 1 +р _т )д ³ ] ^{1 / 4} , [(р 1 +р _г )g ³ /а] ^{1 / 4} , [ад/(р 1 +р _г )] ^{1 / 4} и ^{[ а}д ^/( р 1 +р г ^{)] 1 /} 2 , получим для возмущений следующую линеаризованную систему уравнений:

d v » /dt = — (1/Р г ) V p г + 7 » V 2 v » ,     V v » = 0,                          (2)

где Р г = р » /(р 1 +р г ), 7 г = У г [д (р 1 +р _Г ) 3 /а ³ ] ^{1 / 4} , р 2 =р _г +Др, Р 2 = Р 20 +ДР, ^ 20 = р _г / (р 1 + р _г ), ДР = = ^Др^/(р 1 ⁺ р г ).

Здесь а - коэффициент поверхностного натяжения на границе раздела. Изменение плотности Др найдём из уравнения Менделеева-Клапейрона. Отсюда Др = рДР / RT, где р - масса моля жидкости, ДР = Р - Р _г - перепад давления в приосевой области, R - газовая постоянная, T -абсолютная температура.

Считая C малым, имеем на границе раздела следующее [4]:

(v 1 — v ₂ )n = 0,     (v 1 — v ₂ ) x n = 0,      dC/dt = w 1 ,                    (3)

Р 1 7 1 (du 1 /dz + d w 1 /dx) = Р 2 7 2 (ди 2 /dz + d w ₂ /dx ),

Р i 7 i (dv i /dz + dw i /д y ) = Р 2 7 2 (d V 2 /d z + dw 2 /dy ),

P i - P 2 = (Р 1 - Р 2 )С - (d ² /dx ² + d ² /dy ² )C + 2Р 1 7 i d w i /dz - 2Р 2 7 2 dw 2 /dz.

При z ^ ± to v _г ^ 0.

Здесь n = (-дС/дx, -дС /д y, 1) единичный вектор нормали к поверхности.

Совершая преобразования Фурье по переменным х, у и Лапласа по времени и учитывая, что v _г (t = 0) = 0, С(t = 0) = 0 и v _г , С, d v г /д х, д v _г /дх, dQ/д ^ 0 при | ж, у | ^ ±то , получим, поступая также как и в работе [5], после обратного преобразования Лапласа в линейном по вязкости и приращению плотности приближении следующее уравнение для смещения поверхности от положения равновесия:

d + 25(3 ) ' + ( П О - к АЗ) С = 0,                              (4)

L                 lLL где 5(3) = ^/3171 + /32072 +        2/2 ^^ ^V-/'2'-'^') ^ ПО = к3 + к(31 - М k - вол новое число.

В случае реализации режима движения «а» Ар = (/AP/RT)sinwt. Тогда уравнение (4) при мет вид:

' + 25(3) Ц + ФО — kq sin ш ) С = 0, dt ²           dt

где q = м | АР | /[ДТ (p i + Р т )].

Уравнение (5) представляет собой уравнение Матье с затуханием [6]. Решая его методом усреднения [7], получим для границ (основной) области устойчивости следующее уравнение:

q ² /45(3) ² ^ ² k ² - ⁽ П - ш ² /4 ^{) 2} /5(3) ² ^ ² к ² = 1.

Из анализа этого уравнения следует, что поверхность жидкости неустойчива, если амплитуда возбуждения q >  25(3)шк. При этом на поверхности возникают волны с частотой ш/2 и волновым числом k, определяемым из уравнения:

к ³ + к(3 1 — З _т ) = ш ² /4.

Для отрыва капель с поверхности жидкости необходимо, как показано в работе [8], увеличить амплитуду возбуждения в четыре раза.

При реализации режима движения «b» уравнение (4) примет вид:

^{d 2} l + 25(3) ^dl; + ( П О ± kq ) С = 0.                              (6)

t                     t-tL

Это есть уравнение Мейснера (см., например [9,10]). Будем искать периодические решения этого уравнения. На участках 1 и 2 рис. 2 общее решение уравнения (6) имеет вид:

С 1 = e ^{-5 (3}'^)t (C ₁ sin n 1 t + C ₂ cos n 1 t),

С2 = e-5(/3)t (C3 sin n2t + C4 cos n2t), где J? 1 = (ПО+ kq — 5(3)2)1/2, ^2 = (ПО — kq — 5(3)2)1/2.

Из условий непрерывности на границе участков 1 и 2 при t = Т /2

С1 = С2,    д^/dt = дС2/дt вместе с условиями «воспроизводства» через период Т

С2(Т) = рС1 (0),     дС2/дt|t=т = pдС1/дt|t=o получим систему линейных однородных уравнений для постоянных С 1 , С 2 , С3 , С4 . Из равенства нулю определителя этой системы уравнений, получим для фактора р квадратное уравнение:

p²-2p{cos (Т П 1 /2) • cos (Т Q ₂ /2) - [(^ о — ⁵(Р ) ² )М sin (Т П 1 /2) • sin (Т П ₂ /2) } е ^{- 27г5 (} ^ ) ■ - 4 ' ' = 0.

Периодические решения получаются при p = ± 1. Отсюда для границ области устойчивости получаем cos (ТQi/2) • cos (Тfi2/2) - [(^0 — 5(/3)2)/n1n2]sin(TП1/2) • sin(TQ2/2) = ±сН(2тт5(/3)).    (8)

Знак плюс соответствует «целым» решениям, т.е. колебаниям поверхности с периодом, равным периоду модуляции, а знак минус соответствует «полуцелым» решениям, когда период колебаний поверхности вдвое больше периода модуляции.

Уравнение (8) связывает между собой вязкое трение 6(Р ) с амплитудой и частотой (периодом) модуляции давления ДР.

Заключение

Гармонические или негармонические колебания давления в одной из жидкостей приводят к неустойчивости поверхности раздела этих жидкостей. В зависимости от амплитуды колебаний давления возможно как возбуждение поверхностных волн, так и диспергирование жидкости.