Дисперсия, поглощение и генерация электромагнитных волн в вакууме

Одним из основополагающих принципов современной физики является знаменитый постулат специальной теории относительности (СТО), согласно которому скорость света в пустоте является фундаментальной физической константой и не зависит от выбора инерциальной системы отсчета.

Проблема зависимости скорости света от выбора системы отсчета возникла в физике конца XIX века. Ее появление было связано с тем, что уравнения электродинамики Максвелла являются инвариантными относительно преобразований Лоренца, а механика Ньютона галилеево-инвариантна. Различие между теорией механического движения и теорией закона сил, это движение вызывающих, в законах преобразования при переходе из одной инерциальной системы отсчета в другую, есть серьезнейшее логическое противоречие. Использовав постулат о постоянстве скорости света, и введя релятивистские поправки в уравнения механики, Альберт Эйнштейн устранил противоречия между механикой Ньютона и электродинамикой Максвелла.

В настоящее время специальная теория относительности блестяще подтверждена многочисленными прецизионными экспериментами и всей инженерной практикой человечества, и, фактически, никем не подвергается сомнению. Другими словами, имеет место блестящее согласие теории с экспериментом, подтвержденное более чем вековым ходом развития физики. В соответствии с основным постулатом СТО вакуум не поглощает и не преломляет электромаг- нитные волны.

В то же время хорошо известно, что классическая электродинамика становится внутренне противоречивой при переходе к масштабам расстояний порядка классического радиуса электрона [1, 2]:

Re = S , mc

а излучение и поглощение электромагнитных волн, вопреки Максвеллу, носит дискретный характер. Ньютоновская механика также не согласуется с эмпирическим фактом дискретности атомных и молекулярных спектров излучения и поглощения.

В течение продолжительного времени считалось, что преодоление внутренних противоречий ньютоновской механики и максвелловской электродинамики возможно в рамках квантовой теории. Однако квантовая теория также не лишена внутренних противоречий, а физические причины, приводящие к квантованию полей, до сих пор не нашли должного объяснения в рамках современной физики.

Целью настоящей работы является демонстрация принципиальной возможности преодоления перечисленных выше противоречий, а также обоснование гипотезы о том, что в основе феномена квантования полей лежит эффект поляризации физического вакуума.

Уточненный специальный принцип относительности Эйнштейна

Принцип относительности (и по Галилею, и по Эйнштейну) является конкретной формулировкой принципа объективности научных исследований применительно к физике. Согласно этому принципу все физические законы одинаковы во всех инерциальных системах отсчета. По Галилею расстояния и времена, измеренные наблюдателями, находящимися в разных инерциальных системах отсчета, одинаковы. Это возможно только в том случае, когда измерение длин и времен осуществляется мгновенно.

В специальной теории относительности учтен тот факт, что наблюдатели, находящиеся в различных инерциальных системах отсчета, используют в процессе измерений световые волны, скорость распространения которых хоть и велика, но конечна. Поэтому результаты измерения времени и расстояния, полученные различными наблюдателями, отличаются друг от друга, но связаны взаимно-однозначной зависимостью. При этом переход от одной инерциальной системы отсчета (ИСО) к другой осуществляется с помощью преобразований Лоренца [1]:

x' + vt' x = I

1 - b²

У = У z = z'

ct =

ct' + bx'

V i - b²

Константа c в формуле (2) – скорость света в пустоте, а параметр b равен b = v / c , где v – скорость движения одной ИСО относительно другой. Принцип относительности Эйнштейна позволяет корректно учесть в физической теории тот эмпирический факт, что мы живем в электромагнитном мире, и никакого другого инструмента, кроме света, для измерения чего бы то ни было, в распоряжении у наблюдателя просто не имеется. Другими словами, любое измерение осуществляется, в конечном счете, при помощи световых волн, скорость распространения которых известна из многочисленных независимых экспериментов. При этом во всех экспериментах по определению скорости света измеряется величина

^C exp = < ^C > ± ^{A C} , (3)

где c – среднее значение скорости света, а A c - погрешность измерения.

Постулат о независимости скорости света от выбора системы отсчета неоднократно проверялся экспериментально. Первый решающий эксперимент был поставлен Майкель-соном в 1881 году. Через несколько лет, в 1887 году Майкельсон совместно с Морли повторил свой знаменитый опыт. В этом интерферометрическом эксперименте производилось сравнение скорости света вдоль направления движения Земли с аналогичной скоростью в перпендикулярном направлении. В результате было установлено, что зависимость скорости света от скорости системы отсчета отсутствует.

По-другому результаты этого опыта можно представить в виде:

dc dl A l* ^ A C, (4) где i - длина световой волны, а Alopt - ширина оптического диапазона длин волн.

Альберт Эйнштейн положил результаты эксперимента Майкельсона и Морли в основу СТО и придал преобразованиям Лоренца (2) статус неотъемлемого атрибута любой фундаментальной физической теории.

Задолго до исторического эксперимента Майкельсона и Морли Дж.К. Максвелл создал электромагнитную теорию света, в которой фигурирует скорость света в пустоте c . Уравнения Максвелла для напряженностей электрического E и магнитного H j полей для свободных электромагнитных волн имеют вид:

^ vx н = 1 ^ Е c д t

—►

Vx Е

1 dHH c д t

—

V-H = 0

—

V - Е = 0

и являются лоренц-инвариантными. Уравнения для 4-потенциалов A ^m :

2m c?2 bdt^ -V2Am = 0            (6)

также лоренц-инвариантны.

При переходе от (5) к (6) использовались общеизвестные соотношения:

——

E = —V j —

1 ^A. c Э t

——

H = VxA

калибровка Лоренца

^{1 j +V}- A = 0 • (8) а через A ^m в формуле (6) обозначен 4- потенциал A m = ( j >, A ) .

На первый взгляд, уравнения (5), (6) невозможно модифицировать так, чтобы в них появился показатель преломления, и при этом не были нарушены лоренц-инвариантность и трансляционная инвариантность теории. Однако, это не так.

Известно, что в квантовой электродинамике (КЭД) довольно подробно исследованы эффекты поляризации вакуума, а также нелинейные эффекты типа рассеяния фотона на фотоне [2]. Эффекты эти, как правило, невелики. В области низких энергий они пренебрежимо малы, и только в области высоких энергий становятся заметными. Другими словам, некоторый объем физического вакуума, попавший в поле электромагнитной волны (особенно, в случае высоких энергий), ведет себя как самый обычный диэлектрик – он поляризуется. При этом “голый фотон” взаимодействует с виртуальной материей (электронами, позитронами и другими заряженными виртуальными частицами). В результате этого взаимодействия физический вакуум поляризуется, а электромагнитная волна, увлекающая за собой виртуальную материю, превращается в квазичастицу, которую мы и называем фотоном. Как известно, квазичастица отличается от “голой” частицы именно тем, что представляет собой коллективное возбуждение, масса которого отличается от массы затравочной частицы. Фотон в пустоте - это чрезвычайно легкая частица. Тем не менее, она имеет конечную массу покоя. В случае движения фотонов в среде эффект перенормировки массы может быть чрезвычайно большим (см., например, модель векторной доминантности [9], в рамках которой высокоэнергетический фотон в ядре может самопроизвольно превратиться в любой нейтральный мезон с квантовыми числами фо- тона). Очевидно, что наибольший вклад в процесс взаимодействия электромагнитной волны с физическим вакуумом дают виртуальные электроны и позитроны, поскольку среди всех заряженных элементарных частиц именно они обладает наибольшим удельным зарядом.

Описанный эффект “одевания” частиц и превращения их в квазичастицы подробнейшим образом изучен как в физике твердого тела, так и в ядерной физике. В квантовой электродинамике сходные идеи привели к созданию теории перенормировок.

Все вышесказанное позволяет сделать однозначный вывод. Для того чтобы в рамках классической электродинамики учесть эффекты поляризации физического вакуума, самоорганизации электромагнитных волн в вакууме и превращения их в фотоны, перенести идеи квантовой теории в классическую электродинамику, устранив ее внутренние противоречия, и при этом не нарушить лоренц-инвариантности теории, необходимо обобщить принцип относительности Эйнштейна.

Однако перед тем как дать уточненную формулировку специального принципа относительности, сделаем ряд предварительных замечаний:

• 1.    Уравнения Максвелла содержат константу c , которая интерпретируется как фазовая скорость плоской электромагнитной волны в пустоте.

• 2.    Майкельсон и Морли никогда не измеряли зависимость скорости плоских электромагнитных волн в пустоте от скорости движения системы отсчета, поскольку плоских волн, представляющих собой математическую абстракцию, не существует в природе.

• 3.    Альберт Эйнштейн ни в одной из своих работ не писал о постоянстве скорости распространения электромагнитных волн. В знаменитой статье “К электродинамике движущихся тел” фигурирует постулат о постоянстве скорости света в пустоте.

• 4.    Под светом в специальной тео рии относительности понимается электромагнитное излучение, длина волны которого лежит в очень узком спектральном диапазоне (так называемом, оптическом диапазоне длин волн 0.4 <  l <  0.75 мкм).

• 5.    Любой реальный световой пучок

• 6.    Групповая скорость распространения волнового пакета в среде с нормальной дисперсией всегда меньше его фазовой скорости.

(даже монохроматический импульс лазера) имеет конечные продольные и поперечные размеры, и, следовательно, представляет собой волновой пакет.

С учетом вышесказанного приведем специальный принцип относительности Эйнштейна в новой редакции:

• 1.    Физические законы одинаковы во всех инерциальных системах отсчета.

• 2.    Переход от одной ИСО к другой осуществляется с помощью преобразований Лоренца (2).

• 3.    Константа c в преобразованиях Лоренца (2) и уравнениях Максвелла (5) есть низкочастотный предел скорости распространения фотонов в вакууме с( w es ) :

с = lim с( w rest )

w rest ^ 0 ^V W ^(V) где w ^rest – частота электромагнитных колебаний в системе покоя фотона, причем для любых частот w rest >  0 справедливо строгое неравенство с( w rest ) <  с .

Вся дальнейшая часть работы посвящена обоснованию этого положения. Однако прежде чем приступить к построению нелинейных динамических уравнений электромагнитного поля в физическом вакууме, необходимо провести анализ кинематики квантов электромагнитного поля.

Рассмотрим две системы отсчета: K и K ', причем к - лабораторная система, а к ' -система покоя фотона. В этом случае преобразования Лоренца приобретают вид:

=     с( w rest ) t'

1 - / ² ( w rest )

У = У' = 0

z = z ' = 0

ct =

ct'

7 1 - ■ w ^rest )

причем rest

/(w s ) = ^c(wc^-.             (11)

Частоты и волновые вектора при переходе из системы покоя фотона в лабораторную систему координат преобразуются ана- логичным образом:

rest rest lab =  P(w  ) w x J1 - /32(wrest)

klab rest k = 0 y У klab rest k = 0 z z' lab rest wrest

V1 - /3 ² ( w ^rest )

Здесь и далее индекс rest означает, что значение соответствующей физической величины измерялось в системе покоя фотона, а индекс lab указывает на то, что измерения проводились в лабораторной системе отсчета. Из формулы (12) следует, что

/w ^rest ) = ^ 1 - ( w ^rest / w lab ) ² .        (13)

Поскольку наблюдатель по определению находится в лабораторной системе отсчета, постольку для расчета зависимости скорости фотона от его частоты необходимо найти вид функции:

rest rest lab w = w (w ) .             (14)

Из преобразований Лоренца следует, что w ^rest есть нечетная функция частоты w ^lab . Зависимость эта неизвестна, однако, очевидно, что она является нелинейной.

При приближении к статическому пределу wrest ^ 0 групповая скорость электромагнитного волнового пакета в лабораторной системе отсчета стремится к “скорости света в пустоте” /3(wrest) ^ 1. Отсюда следует, что rest lab            lab 3 lab\ w Iw J = (w ) -^lw J,        (15)

где спектральная функция Q(wlab J является четной функцией частоты wlab , причем q (wlab = 0) = c ^ 0 . Далее в работе рассматриваются только физические процессы в области низких частот, начиная от wrest = 0 вплоть до порога нарушения стабильности вакуума hw™*, = mc2,               (16)

tresh где m – масса покоя электрона.

Поляризацияэлектромагнитного вакуума

Соотношение (9) предоставляет возможность построить нелинейные уравнения Максвелла в пустоте посредством учета поляризационных свойств физического вакуума,

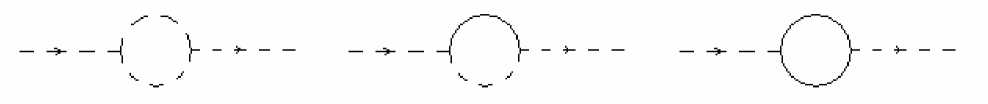
Рис. 1. Процесс g ^ 2 g ^ g

Рис. 2. Процесс g ^ e ^т + g ^ g

Рис. 3. Процесс g ^ (e " ⁺ e ⁺ ) „r_rt ^ g

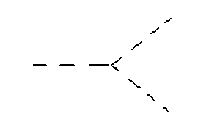
Рис. 4. Процесс g ^ 2 g

Рис. 5. Процесс g ^ e ^T + g Рис. 6. Процесс g ^ e + e ⁺

определяемых, в первую очередь, самодей-ствием электромагнитной волны, а также ее взаимодействием с виртуальными электронами, позитронами и другими частицами.

Учет вакуумных токов произведем по аналогии со стандартным способом обобщения уравнений Максвелла в пустоте на случай наличия зарядов и токов:

_     — 4тг —

Vx H = — j_mc c

1 эб_ ⁺ c Э t

——

VxE =

1 dEH c Э t

—

V-H = 0

—

v ■ E = 4 pr„aC

где ( c r „ _ac , j_vac ) - плотность тока поляризации вакуума. На языке вектор-потенциалов уравнение (17) приобретает вид:

C 1 2 ^^ - ^V’ ^A = X p ’ a ⁽ x ⁾ , ⁽¹⁸⁾ которое должно быть дополнено условием калибровки Лоренца:

^ a : = о

Э x ^:

.

Из уравнения (18) видно, что электромагнитное поле поляризует вакуум. Другими словами, виртуальные электроны и позитроны начинают двигаться с ускорением. В результате в плотности тока поляризации вакуума появляются члены типа

■ m        1 Э2Am j«.c(x )~—^-T c Э t

1 На всех диаграммах в настоящей работе штриховые линии отвечают распространению фотонов, а сплошные – распространению электронов и позитронов.

отвечающие за появление у физического вакуума показателя преломления n , не равного единице. Процессу преломления световой волны в результате взаимодействия с самой собой в низшем порядке теории возмущений соответствуют диаграммы 1-3¹.

Нелокальность теории приводит к появлению в выражении для плотности тока поляризации вакуума членов типа лучистого трения (т.е., к поглощению фотонов):

1 Э ³

j L ( x )~ c 3 A m ( x ) . (21)

Этому току соответствуют диаграммы 4-6, причем канал g ^ 2 g является открытым при любых энергиях исходного фотона, а каналы g ^ e ^ + g и g ^ e ⁺ + g открываются, как только энергия фотона в системе его покоя превышает порог распада h w >  _mc ² . Особо подчеркнем, что рамках развиваемого подхода электродинамика превращается в теорию с бегущей константой связи. Поэтому процессы типа 5 не запрещены законом сохранения заряда.

Именно из-за присутствия членов типа (21) в выражении для плотности индуцированного тока поляризации вакуума у показателя преломления вакуума появляется мнимая часть. В свою очередь, отсутствие определенной четности у плотности индуцированного тока поляризации физического вакуума обусловливает необратимость микропроцессов и определяет существование Стрелы Времени. При этом “трение” фотонов о физический вакуум происходит, в основном, из-за их взаимодействия с виртуальными электронами и позитронами. Этот процесс приводит к тому, что первичный фотон сам начинает излучать электромагнитные волны, которые также са-

моорганизуются в фотоны. В результате происходит затухание и расплывание исходного волнового пакета по мере того, как он теряет энергию за счет нелинейности плотности вакуумного тока j ^ac ( x ) , как функции вектор-потенциала A m (x ) .

Постоянная Планка п попадает в классическую электродинамику в результате выполнения условия:

r E ² + H² --dV = п ■ w

^J 8 p               ’

которое справедливо в любой системе отсчета, поскольку как энергия, так и частота представляют собой нулевые компоненты соответствующих 4- векторов.

В рамках этой философии у фотона автоматически появляется масса покоя, которая строго зависит от частоты w ^rest в системе покоя фотона, причем масса фотона содержит как вещественную, так и мнимую части:

rest

/ rest \ 2          / rest \ 2 • ^ (w )           о х mphoton (w )c = m0(w )c - i 2  . (23)

В итоге скорость света убывает с ростом w ^rest , а масса фотона строго равна нулю только при w rest = о .

Соотношения (22) и (23) дают исчерпывающий ответ на вопрос о причинах квантования электромагнитного поля. Наличие нелинейного тока поляризации физического вакуума приводит к тому, что вместо максвелловской плоской электромагнитной волны, распростирающейся во всем пространстве, как в продольном, так и в поперечном направлении, образуется компактный сгусток электромагнитной материи – фотон. Кроме того, они однозначно подтверждают точку зрения А.А. Логунова [13] на природу сил тяготения.

Для того чтобы формальную запись уравнения (18) превратить в основное уравнение новой физической теории, необходимо установить явный вид плотности вакуумного тока j_v ^m _ac ( x ) .

Идея, лежащая в основе решения этой задачи, состоит в следующем. Выражение для плотности вакуумного тока надо получать исходя из того, что ускорение виртуальных электронов и позитронов, находящихся в объеме фотона, пропорционально напряженности электрического поля ( a e _т ~ E ).

Как известно, электрические заряды, движущиеся с ускорением, излучают электромагнитные волны. Исходный фотон при этом теряет часть своей энергии. За счет этого у физического вакуума появляется коэффициент поглощения k _v . Другими словами, физический вакуум представляет собой несколько необычную диссипативную систему. Однако и для столь экзотической диссипативной системы выполняются дисперсионные соотношения, представляющие собой одну из форм математической записи принципа причинности в физике. Поэтому показатель преломления физического вакуума n v также отличен от нуля. Далее везде, где это не оговорено специально, мы будем называть показателем преломления физического вакуума комплексную величину n ( w ) = n v + i k v . Вещественная часть показателя преломления n в приближении электромагнитного поля малой интенсивности пропорциональна плотности материи (энергии) Re n(x )~ W(x ) = T⁰⁰ (x ) , а мнимая часть пропорциональна градиенту плотности материи Im n(x )~ ( s ■V W(x ) j (здесь j - оператор спина фотона, см., например, работы [5,6], в которых дан подробный анализ оптической модели упругого рассеяния и эффектов спин-орбитального взаимодействия).

Из этих соображений можно установить вид плотности тока j ^m ( x ) поляризации физического вакуума. Определим ток j m (x ) как свертку потенциала A ^m ( x ) с тензором классической (т.е., не квантовой!) плотности поляризации физического вакуума П ml (x — x ' ) :

j m (x ) = i J A l ( x ') ■ П ml (x — x')dQ' . (24)

Интегрирование в (24) осуществляется по инвариантному 4- объему d Q = dx ■ dy ■ dz ■ cdt .

В приближении самосогласованного поля малой интенсивности тензор П ml ( x — x ' ) пропорционален тензору энергии – импульса электромагнитного поля, поэтому

^П ml ⁽ x ) = Ak .

eff

⁺ i u eff s'

T ml (x ) . (25)

У x r             ^{v 7}

В (25)

k ef    k о + k 1 ■ e + k 2 ■ e ² + k 3 ■ e ³ + k 4 ■ e ⁴ + ... (26)

где keff – эффективный коэффициент поляризуемости физического вакуума, а e – заряд виртуальной частицы, взаимодействующей с электромагнитной волной. Особо подчерк- нем, что e < о для электронов, и e > о для позитронов.

В (25) фигурирует тензор энергии-импульса электромагнитного поля T ml ( x ) [1]:

T ml ( x ) =    [- F mn ( x Wl ¹ ( x ) + ¹ g ml F" ( x ) F„ ( x ) ' ,(27)

4 p (                      4                    J ^{v 7}

где F mn ( x ) - тензор электромагнитного поля:

ЭА - A F (x) = -An--m mA '   - xm - xn .

В приближении (25) вклад всех видов виртуальной материи, отвечающих за возникновение обратной связи между электромагнитной волной и физическим вакуумом, учитывается интегрально с помощью эффективной величины – коэффициента поляризуемости физического вакуума k eff .

В соотношении (25) также присутствует оператор спина фотона s r . Его компоненты s ¹ = ^s , s² = S y , s ³ = s z в декартовом базисе имеют вид [12]:

В формуле (29) использована нормировка

(s ⁰ ) ² - (S) = I ,           (30)

где

' 1 о o '

I = 0 10 0 0 1 ч 7

единичная матрица. Спинорный коэффициент поляризуемости физического вакуума u eff в формуле (25) подлежит определению из дополнительных условий.

В разложении (26) нулевой член соответствует физическим процессам, изображенным на диаграммах 1 и 4, первый член описывает вклад диаграмм 2 и 5, второму члену разложения отвечают диаграммы 3 и 6. Таким образом, в соотношении (25) учтен как вклад са-модействия электромагнитного поля, так и вклад взаимодействия электромагнитной волны с виртуальной заряженной материей.

Приближение полей малой интенсивности позволяет замкнуть систему уравнений электродинамики вакуума, в которую, строго говоря, необходимо добавить уравнения Дирака для электронов, позитронов, протонов, и других заряженных частиц со спином

1/2 . Кроме того, точная система уравнений электродинамики физического вакуума должна включать в себя уравнения для тяжелых лептонов, адронных резонансов, различных мезонов, а также калибровочных бозонов.

В рамках настоящей работы анализируются только физические причины квантования электромагнитного поля. Поэтому всюду далее мы ограничимся анализом слабых полей и исследованием эффекта поляризации вакуума в скалярном приближении u _eff = 0 .

Необходимо также подчеркнуть, что в рамках развиваемого подхода постоянная Планка имеет физический смысл основной характеристики фотона. Другими словами, постоянная Планка появляется в классической электродинамике, как неотъемлемая характеристика волнового пакета, каковым является фотон, причем групповая скорость этого пакета подчиняется стандартному соотношению:

Rec( w_t ) = Re

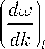
lim Re c( w_t )

^w l ^⁰ ___________

Re n ( w l )

c

Re n ( w l ) .

Отметим, что соотношение (27) имеет смысл только в лабораторной системе отсчета, т.к. в системе покоя фотона его групповая скорость равна нулю по определению.

Электродинамикав системе покоя фотона

Для того чтобы решить уравнение (18) с учетом калибровки (19) необходимо записать эти уравнения в системе покоя фотона. В этой инерциальной системе отсчета выражение для 4- потенциала электромагнитного поля в приближении скалярной оптики ( u = 0 ) имеет вид:

A^ t ( x ) = f m ( t ) -T m (Г .              (33)

Через 4-вектор tm (x) = (T0, T) выражается распределение энергии и импульса электромагнитного поля по объему фотона, а эволюция волнового пакета во времени описывается функцией f m(t). Вектор-потенциал ATme^t (x) факторизуется в системе покоя фотона, поскольку в этой системе отсчета электромагнитное поле представляет собой стоячую сферическую волну. В силу того, что в системе покоя фотона его импульс по определению равен нулю, электромагнитное поле становится потенциальным. В этом случае выполняется условие T = о, означающее, что магнитное поле в системе покоя фотона равно нулю (й = о). Зависящий от координаты Г сомножитель, входящий в нулевую компоненту 4- потенциала Amest (x) назовем структурной функцией фотона и обозначим его через T0(F) = T(F). Очевидно, что электрическое поле в объеме фотона пропорционально градиенту структурной функции:

Е = - f (t ) ■ VT,              (34)

где f (t ) = f ⁰ ( t ) .

В уравнении (18) присутствует плотность вакуумного тока jm(x) = (j0,j.                  (35)

Так как в системе покоя фотона электромагнитное поле является потенциальным, отлична от нуля лишь одна компонента тока ( j ⁰ = j ), и фотон в физическом вакууме приобретает ненулевой электрический заряд², зависящий от частоты w ^rest . Далее для сокращения записи мы будем опускать индекс rest .

С учетом вышесказанного вид тока поляризации вакуума в пределе слабых полей определяется однозначно. В самом деле. В импульсном представлении тензор энергии-импульса электромагнитного поля имеет вид:

T ml (k ) = W 2 k m k ¹ .           (36)

w

В системе покоя фотона его импульс и волновой вектор равны нулю, поэтому у тока (24) отлична от нуля лишь одна компонента:

Е

T ⁰⁰( x) = L ,                  (37)

8 p и с учетом этого обстоятельства ток (24) принимает вид:

j(x ) = i k f J A o (x')T⁰⁰ (x - x ' ) d Q'   (38)

Подставляя (34) в (38), мы получаем выражение для плотности тока поляризации вакуума:

j ( x ) = i w J f ( t ') ■ T ( ^F ' ) ■ f ( t - 1 ') ■ VT ( ^F - ^F')|² d Q' (39)

и уравнение для волновой функции фотона |4°. - V²1 ■ f ( t ) ■ T ( ^F ) = i '' J f ( t ' ) ■ T ( ^F ' ) I f ( t - t ' ) ■ VT ( ? - ? ' )| ² d Q' I С О t I 2 C °

Еще раз подчеркнем, что соотношения (32)-(35) справедливы только в системе покоя фотона.

Строго говоря, на уравнении (40) исчерпываются внутренние возможности классической электродинамики в задаче о нахождении дисперсионных соотношений для физического вакуума и вычислении структурной функции фотона. Это обусловлено тем, что величина плотности вакуумного тока

j ( x ) = i J f ( t ' ) ■ T ( ? ' ) ■ f ⁺ ( t - t ') ■ f ( t - 1 ') ( VT⁺ ( ? - ? ' ) ■ VT ( ? - ? ' ) ) d Q' 8 pc ^J

(41) содержит неизвестную величину – постоянную поляризуемости физического вакуума k eff . Тем не менее, на основе уравнения (41) можно оценить масштаб нелинейных эффектов, приводящих к квантованию электромагнитного поля. Для этого заметим, что функция

W (t , F ) = 8^ - ( f ⁺ (t ) ■ f(t ) ) ( VT⁺ ( F ) ■ VT ( F ) ) (42) имеет смысл плотности энергии электромагнитного поля. С учетом этого обстоятельства представим (41) в следующем виде:

j(x ) = ^г k f J f ( t ') ■T ( ^F ' ) ■ W(t - t ', ^F - ^F ' ) d Q' .(43)

Для дальнейшего продвижения заметим, что в формуле (43) интегрирование по t ' при анализе затухающих решений осуществляется в пределах t ' е ( -^ , t ] , так как электромагнитная волна не может взаимодействовать сама с собой с опережением по времени.

В силу того, что W ( t , ^F ) представляет собой плотность энергии фотона, распадающегося в собственной системе отсчета, мы можем считать, что

, F ( Г ) ,F.

W ⁽ t , r ) = exp ^-- t ■ W , ⁽ r ) . (44) l й J

На данном этапе рассмотрения конкретная зависимость коэффициента поглощения вакуума от частоты несущественна. Необходимо отметить только то, что величина Г = Г ( w ) , является четной функцией частоты w (т.е. Г ( w ) = Г ( - w ) ) в силу того, что любые диссипативные процессы являются необратимыми.

Очевидно, что для пространственной плотности электромагнитной энергии выпол- няется соотношение Планка

J W , ^(r)dV = m photon ⁽ w ^{)c 2} = h w .     (45)

Подставляя (44) в (43), получаем:

3 ( x ) = i k Г f ( t ')■T(F') ■ exp I— ^ ( t - t ')! w , (г - r') dV 'dt ' c                          ( h )

Функция f(t) является быстроосцилли-рующей, и в нулевом приближении можно считать, что r f (t) = exp (-(w - ig)t) ,         (47)

где³ g = —. В результате плотность тока поляризации вакуума принимает вид:

j ( x ) = i k f J e ^- i ^{( w -} ig ) F' ) ■ e ^-2 g ⁽ t ^- t ^- W , ( F - r ' ) dV dt ' .(48)

Выполняя в (48) интегрирование по t¹ , получаем:

; t      /           . ,      ,           ,      exp ( - i ( w - ig ) t )

exp ( - i ( w - ig ) t ' - 2 g ( t - t ') ) dt = i --------_:------- (49)

■                                                                       ^g

Подставим выражение (52) в уравнение (53):

[ ( w - ig )²

I           c c¹

-V ²

e ~ i ( w - i g ) t

■T ( ? )

4 pkeff   hw T(r) ■ e“i(w-ig) t c2 w + i g

С учетом того обстоятельства, что структурная функция фотона по определению не

зависит от времени, приходим к следующему выражению

V ² T ( F ) =

4 Pk ff h w    ( w - i g ) ²

c²   w + i g       c

T ( r ) . (55)

В системе покоя фотона его структурная функция обладает сферической симметрией, и уравнение (55) превращается в обыкновенное дифференциальное уравнение:

-2 Tri r ² Fr|T( r ) + k ^( w ) T ( r ) = 0 , (56) r a r ( a r)                               ^{v 7}

где

и мы приходим к следующему выражению для плотности вакуумного тока:

k eff exp ^(- i ⁽ w ^- i g ) t ⁾                    ГЛ

3 ⁽ x ) =------ I T ( r ) ■ w , ( r - ^{r )d} V .(50) c       w + i g     J                      ^{v 7}

Воспользуемся общеизвестным фактом малости размеров элементарных частиц и высочайшей точности результатов квантовой электродинамики, которая, как известно, разработана в локальном приближении. В этом случае плотность энергии электромагнитного поля в объеме фотона можно считать сосредоточенной в точке. В приближении локального взаимодействия

W , ( F ) % W ₀₀ ■ d (r - r ' ) = h w ■ d (Г - r ) , (51) и выражение для плотности тока поляризации вакуума упрощается:

k eff exp ^(- i ⁽ w ^- i g )t ⁾

j ⁽ x ) = ^{- h} w                       ^{T (} r ) . (52)

c w + i g

Построим уравнение для структурной функции фотона. Для этого представим (18) в виде:

k ²( w ) =

^{( w -} i g ^{) 2}

4 PK_{e ff} h     w

--- -

2 , c     w + i g

решение которого имеет вид:

T(r ) = T o ( k )e ^x p < i ^{kr )} .           (58)

r

Т.е., структурная функция фотона в области частот, для которой выполнятся условие

Re ( k ( w ) ) >  0 , (59) представляет собой сферическую стоячую электромагнитную волну. Из формулы (57) следует, что при w ^ o мнимая часть волнового числа положительна:

1 d ²

c ² d t ²

-V ²

■ f (t ) ^T ( r ) =— 3 ( x ) . c

3 Строго говоря, вместо (47) надо было бы использовать вещественную функцию f (t) = cos (wt) ■ exp (-gt), поскольку мы имеем дело со стоячей волной. Однако в контексте решаемой задачи применение математического трюка, позволяющего существенно упростить выкладки, не влияет на конечный результат.

Im ( k ( w ) ) >  0 (60) и структурная функция фотона превращается в потенциал Юкавы. Это означает, что электрический заряд фотона (бегущая константа связи в электродинамике) в среднем равен нулю, а в каждый момент времени отличен от нуля, но экранирован, как и любой заряд, помещенный в диэлектрик. В результате фотоны поляризуют вакуум гораздо сильнее, чем электроны. И это не удивительно, поскольку для электронов в их системе покоя волновой вектор k r = 0 , и выражение (58) переходит в известный закон Кулона. Из выражения (58) также следует, что геометрические размеры фотона в системе его покоя имеют порядок длины волны, что полностью согласуется со здравым смыслом. Наконец, найдем постоянную интегрирования T ₀ из условия (45). Для этого используем тот факт, что

VT(r) = -0Fr exp(ikr^ = -0Fr Iik o r     r [ откуда следует, что

exp ( ikr ) exp ( ikr )

r

r2

, (61)

она равна

A ( kr ₀) % ₁-----:---

I ^{k (} w ) ■ ^r 0

ж ( F ) = -° ik ⁰       8 p

exp ( ikr )    exp ( ikr )

—

r

2 r

.

- 2

* % 2 cr              (70)

причем под k (без аргумента) мы подразуме-

и вытекает уравнение на — 0 :

2 fT° ■ ik J 8 p

exp ( ikr )    exp ( ikr )

—

r

2 r

dV = h w . (63)

Как уже упоминалось выше, эффекты поляризации вакуума чрезвычайно малы, а диссипация энергии фотона происходит столь медленно, что для незначительного изменения длины электромагнитной волны в оптическом диапазоне фотон должен преодолеть расстояния в сотни миллионов световых лет. Поэтому влияние величин k eff и g на нормировку структурной функции сводится к тому, что интеграл (63) сходится на верхнем пределе. Воспользуемся соотношением

( ikr — 1) ■ ( — ik*r — 1) = 1 + | k ( w )| ² r ² + 2 Re k ( w ) ■ r , (64) и выполним в (63) интегрирование по угловым переменным. В результате уравнение на — 0 принимает вид:

- _ ° J e ^— 21m ^{k (} w> r .[ 1 ₊ k ( w )| ² r ² ₊ 2 Re k ( _ш ) ]. r ^{— 2} dr = h w .(65)

Интеграл (65) можно представить в виде суммы интегралов, два из которых расходятся на нижнем пределе в полном соответствии с тем, что классическая электродинамика становится внутренне противоречивой в области малых расстояний порядка классического радиуса электрона. В соответствии с этим введем фактор обрезания

ваем | k ( w )| . Поскольку по своему физическому смыслу радиус обрезания r ₀ = const , мы можем найти зависимость Т ₀ = T ₀( k ) . Высокая точность, с которой постоянная Планка действительно является фундаментальной физической константой, позволяет найти величину Т ₀ :

T ₀( k ) = V 2ckr₀ h .

ro

^{A ( kr} 0 ) = I ^{k (} w ) Г J e

■^{2Im k ( w} ) ^r .[ 1 + | k ( w )| 2 r ² + 2Re k ( w ) ]■ r

2 ^dr ,(66)

где r ₀ - радиус обрезания. Из формулы (66) следует, что

T 2 /

-2 - A ( k ^) = h w ,

и мы, таким образом, получаем явное выражение для постоянной Планка:

h       A ( kr 0 ) ,

откуда видно, что постоянная Планка действительно характеризует свойства электромагнитного волнового пакета, называемого фотоном. В приближении низких частот

Из формулы (71) видно, что чем выше энергия фотона, тем больше амплитуда его структурной функции T ₀( k ) , и тем меньше ег о эффективный радиус ~ k ^{— 1} . Следовательно, поперечные размеры фотона (релятивистский инвариант!) имеют порядок длины его волны, и таким образом, лимитируют точность измерения координаты электрона в квантовой теории. Отсюда автоматически получается соотношение неопределенности Гейзенберга A p ^xx ~ h и вытекает необходимость отказа от ньютоновской механики и перехода к квантовой механике.

Вывод: вероятностное толкование волновой функции электрона в нерелятивистской квантовой механике имеет право на существование уже хотя бы потому, что мы измеряем координату электрона, бросая на него фотоны, каждый из которых имеет конечные поперечные размеры. Другими словами, в рамках развиваемого подхода процедура измерения в квантовой механике сводится к решению задачи кавалера де Мере.

В процессе анализа соотношения (63) мы сталкиваемся со стандартной для практически всех версий теории поля (как классической, так и квантовой) – расходимостью интеграла (63) на нижнем пределе. Для того чтобы устранить эту расходимость, мы ввели в соотношение (63) некий эффективный радиус обрезания r 0 . В качестве естественного параметра обрезания в теории самоорганизации электромагнитных волн в физическом вакууме логично выбрать величину, пропорциональную классическому радиусу электрона (1). При таком выборе параметра обрезания мы приходим к соотношению:

T o ( w ) = е • , (72) mc ²

физический смысл которого абсолютно прозрачен. Из (72) следует, что амплитуда структурной функции фотона пропорциональна модулю заряду электрона и корню квадратному из отношения его энергии к энергии выхода на массовую поверхность виртуальных электронов (позитронов), находящихся в объеме фотона. Другими словами, канал распада фотона на электрон (позитрон) и фотон открывается, как только мгновенный электрический заряд фотона в его системе покоя становится равным электрическому заряду электрона (позитрона). Этому процессу соответствует диаграмма 5.

Отметим, что канал двухчастичного распада фотона на электрон (позитрон) и фотон в стандартной квантовой электродинамике строго запрещен законом сохранения электрического заряда. Учет эффектов поляризации вакуума приводит к появлению у фотона не только отличной от нуля массы покоя, но и мгновенного электрического заряда. В этом случае каналы распада фотона g ^ е ■ g и g ^ е ■ + g становятся открытыми.

Следует особо остановиться на том, что поскольку волновая функция фотона в системе покоя является быстроосциллирующей функцией времени, то средний по времени электрический заряд фотона с огромной степенью точности равен нулю, а знак и величина его мгновенного заряда определяются моментом времени, в который он взаимодействует с виртуальной частицей. На языке фейнмановских диаграмм анализируемые процессы “самопреломления” и “самопоглоще-ния” электромагнитной волны описываются приведенными выше диаграммами 1-6. При этом в момент распада фотона (т.е. в вершине соответствующей диаграммы) величина и знак его мгновенного заряда совпадают со знаком и величиной электрического заряда частицы, рождающейся из вакуума4.

Из вышесказанного следует, что физической причиной обрезания интеграла пол- ной энергии фотона на нижнем пределе является спонтанное нарушение стабильности электромагнитного вакуума. Другими словами, электрическое поле в объеме фотона высокой энергии становится столь интенсивным, что выбивает из вакуума электроны, позитроны и другие массивные частицы. С формальной точки зрения расходимость интеграла (63) связана с тем, что при высоких энергиях фотон уже нельзя описывать одним нелинейным волновым уравнением (18). Его необходимо дополнить уравнением Дирака, описывающим эволюцию электронов и позитронов, рождающихся из физического вакуума в интенсивном электромагнитном поле. При еще более высоких энергиях фотонов аналогичный механизм приводит к рождению протонов, нейтронов и т.п. При этом не исключено, что процессы образования адронов связаны не только с наличием в пространстве электромагнитного поля, но и с присутствием в нем виртуальной кварк-глю-онной материи. Таков универсальный механизм генерации вещества во Вселенной. В заключение этого раздела добавим, что фотоны сверхвысоких энергий, способные “выбить” из вакуума “весомую материю”, могут рождаться как в результате материальных астрофизических процессов (например, при взрывах Сверхновых), так и в результате флуктуаций физического вакуума, которые приводят к появлению нарастающих во времени решений уравнения (40):

A rrest ⁽ x) = f ^(t ) . ^Tr) = exp ( - i ⁽ w + i g )t ) ^T r ) . (73)